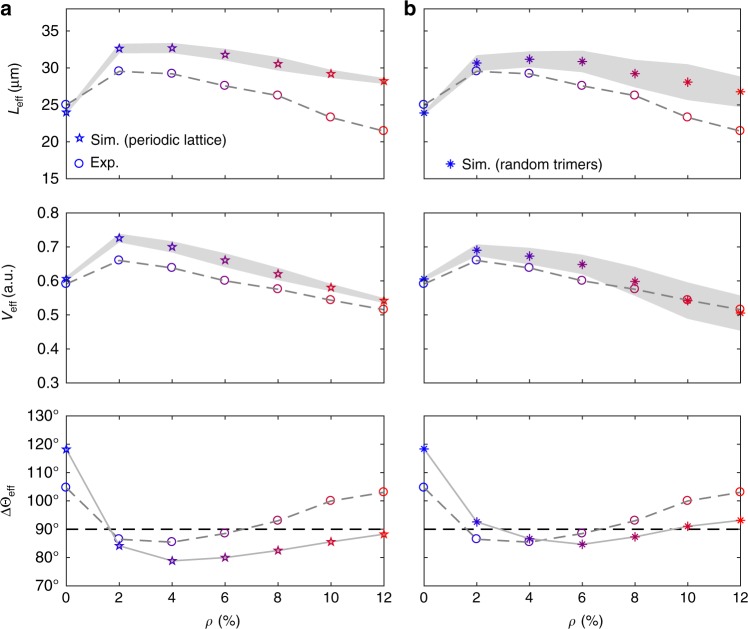
Fig. 6.

Influence of obstacle distribution. a, b Simulated average effective propagation distance L_eff, normalised average effective propagation speed V_eff and average change in effective propagation direction ΔΘ_eff as a function of the obstacle density ρ for chiral active particles self-propelling through a circular area of radius R = 25 μm containing obstacles distributed according to a triangular periodic lattice (a) (Supplementary Fig. 5b and Methods) and a random distribution of non-overlapping trimers (b) (Supplementary Fig. 5c and Methods). The interactions with the obstacles include all three cell–obstacle interaction terms: repulsive interactions, forward-scattering events and tumble-collisions (Methods). Each value is obtained from averaging over 3000 different trajectories. The shaded area around the average values of L_eff and V_eff represents one standard deviation. The solid line connecting the values of ΔΘ_eff is a guide for the eyes. The corresponding probability distributions of the change in effective propagation direction Δθ_eff are shown in Supplementary Fig. 8. The corresponding experimental values (Figs. 1 and 2) are shown for reference (circles)