Fig. 6.

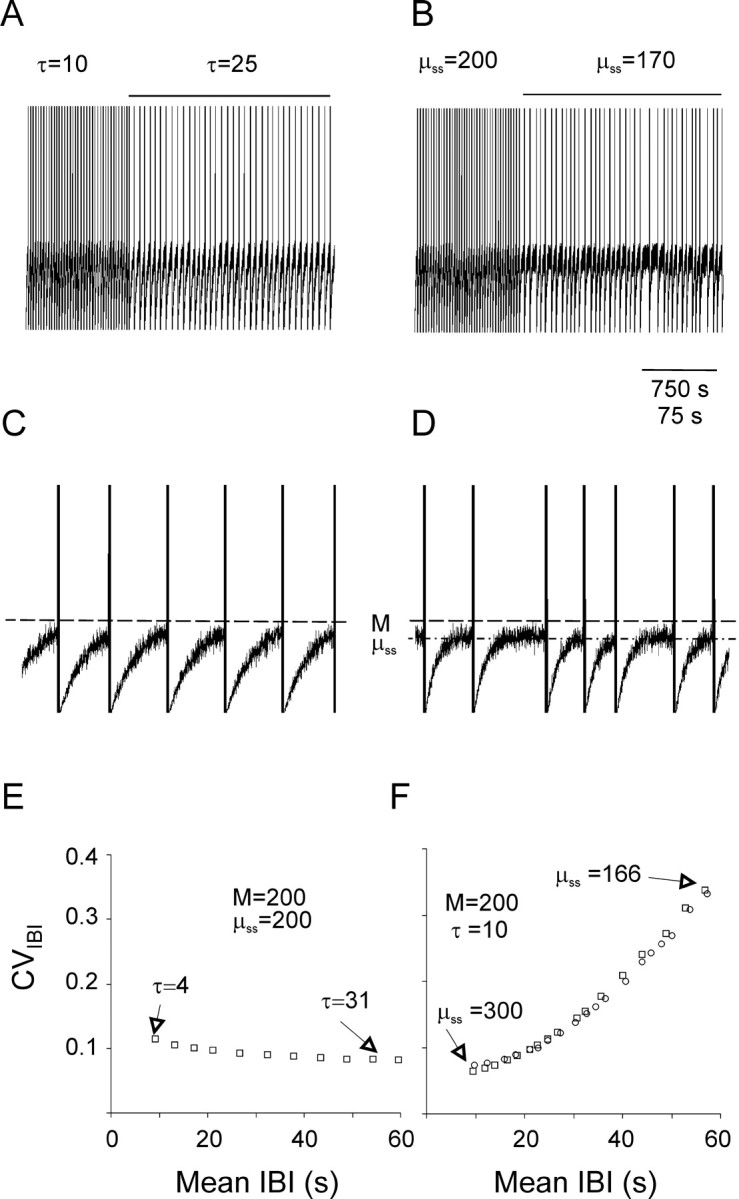
A three-parameter computational model simulated the effect of ZD-7288 on nIB frequency and regularity.A–D, Simulated sequences of nIBs are plotted at a slow (A, B) and a 10-fold faster (C, D) time base. Simulated nIBs were generated by assuming that the mean instantaneous sEPSP rate (μ) is reset to 0 after each burst and then relaxes exponentially to an asymptote (μ_ss) with a time constant τ. Fluctuations around μ were generated by a Poissonian random-number generator; each time a fluctuation crossed the thresholdM (dashed line in C andD), a burst was assumed to be triggered. InA and B, the initial part of the trace was computed using the values M = μ_ss = 200 and τ = 10 sec; during the time indicated by the horizontal lines above the trace, either τ (A, C) or μ_ss(B, D) were changed to the values indicated (μ_ss is also indicated by the dashed-dotted line in D). The traces represent the value of μ, except that the occurrence of a burst is indicated by a vertical line of arbitrary height. Note that increasing τ (A,C) reduced the frequency of bursts without affecting their regularity, whereas reducing μ_ss (B,D) affected both the frequency and the regularity of the bursts. E, The simulated CV_IBI versus the simulated mean IBI, computed using the indicated values ofM and μ_ss while varying the value of τ as indicated. Note that changing τ had very little effect on the CV_IBI. F, The simulated CV_IBIversus the simulated mean IBI, computed using the indicated values ofM and τ while varying μ_ss as indicated (squares). Note that changing μ_ss affected in parallel both the mean IBI and the CV_IBI. Changing Mfrom 140 to 238 while keeping μ_ss = 200 generated data points (circles) that fell along the same curve generated by changing μ_ss while keeping Mconstant.