Encounter complexes and hidden poses of kinase-inhibitor binding on the free-energy landscape

Significance

Molecular recognition via protein–ligand binding is essential for biomolecular functions. Current understanding of ligand recognition is mostly brought from a bound state structure resolved by X-ray crystallography. Using molecular dynamics simulation with enhanced sampling techniques, we here characterize multiple bound poses and transient encounter complexes of an inhibitor kinase on the statistically converged free-energy landscapes. Our simulations propose parallel binding pathways connected through encounter complexes, highlighting the importance of early binding processes. Determination of transient encounter complexes is still difficult experimentally, and the present finding helps to understand the process and widens the possibility of drug compound design.

Abstract

Modern drug discovery increasingly focuses on the drug-target binding kinetics which depend on drug (un)binding pathways. The conventional molecular dynamics simulation can observe only a few binding events even using the fastest supercomputer. Here, we develop 2D gREST/REUS simulation with enhanced flexibility of the ligand and the protein binding site. Simulation (43 μs in total) applied to an inhibitor binding to c-Src kinase covers 100 binding and unbinding events. On the statistically converged free-energy landscapes, we succeed in predicting the X-ray binding structure, including water positions. Furthermore, we characterize hidden semibound poses and transient encounter complexes on the free-energy landscapes. Regulatory residues distant from the catalytic core are responsible for the initial inhibitor uptake and regulation of subsequent bindings, which was unresolved by experiments. Stabilizing/blocking of either the semibound poses or the encounter complexes can be an effective strategy to optimize drug-target residence time.

Drug compounds have been traditionally designed by optimizing their equilibrium binding affinity (e.g., dissociation constant K_d) to a target protein. Many designed compounds still lack in vivo efficacy, raising the importance of kinetics-based compound design (1, 2). In the past decade, the “residence time concept” has been extensively tested, where the drug compound is design to reside in the vicinity of the target protein (3). This kinetics-based design can potentially increase the selectivity to the target protein and also better integrate with pharmacodynamics and pharmacokinetics design (4). In addition to the bound state structures, obtaining an exhaustive mapping of the drug binding landscape is also desired. However, obtaining such mapping experimentally at the atomic level still remains a significant challenge.

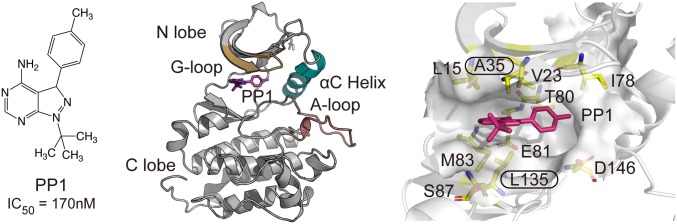
Protein kinases (PKs) regulate signal transductions in cells and their dysfunction can cause several diseases, making them an important drug target, particularly for cancer treatment (5, 6). Designing a selective PK inhibitor is a significant challenge because the inhibitor competitively binds to a highly conserved ATP pocket (Fig. 1) (7). The regulatory residues forming the pocket involve the hinge and the gatekeeper residues (catalytic core), where ATP directly binds, as well as a Gly-rich loop (G-loop or P-loop), an α-helix (αC-helix), and an activation loop (A-loop). The current inhibitor design heavily relies on the atomic structures of the ATP binding site, particularly those of the catalytic core, at bound states obtainable from X-ray crystallography (8, 9). However, the inhibitor selectivity is often a result of the combined contributions of the regulatory residues (10, 11), and the regulation mechanism remains unknown. The residues distant from the catalytic core could play an important role during the binding processes besides the bound state stabilization. Recent experiments using NMR and fast kinetics measurements propose a 2-step binding model consisting of a fast binding followed by a slow induced fit process (12). Elucidating the structural features of binding processes is critical for understanding the regulation mechanism at the atomic level. Yet, structures of transient intermediates such as encounter complexes are still unknown.

Fig. 1.

Structure of the PP1-Src complex. (Left) Chemical structure of PP1 and experimental IC₅₀ (45). (Middle) PP1 bound model from X-ray structures (PDB ID: 1Y57 and 1QCF). (Right) PP1 and 10 binding site residues that were treated as the solute in gREST. The distance between the COMs of PP1 and 2 binding site residues (Ala35 and Leu135) was used as a reaction coordinate for REUS.

Molecular dynamics (MD) simulations, which provide atomic-level details of dynamical processes, are increasingly used for calculating drug-target binding pathways and kinetics, as well as thermodynamics (13–16). Nowadays, MD simulations are able to reach microsecond timescales and observe binding events. Binding pathways and the kinetics extracted from these simulations, however, suffer from large statistical uncertainty, because it is difficult to observe multiple binding and unbinding events within the available computational time, even when using specialized hardware (17, 18). In overcoming the difficulty, parallel trajectory approaches predict binding pathways and kinetics at longer timescales using short-time simulation data (19–22), while various enhanced sampling methods characterize drug-target binding, with a particular focus on unbinding kinetics, by effectively crossing high energy barriers (23–31). Currently, unbinding kinetics and their molecular determinants can be reasonably estimated and directly compared with experiments, though obtaining converged free-energy landscapes to map all of the key intermediates along the pathway remains a challenge. In this work, we focus on the 2D replica-exchange method—REST/REUS, a combined replica-exchange umbrella sampling (REUS) (32, 33) and replica exchange with solute tempering (REST) (34, 35). This combined approach complements drawbacks in each method to further enhance the sampling and can precisely predict protein–ligand bound structures ab initio (36). Here, we extend the method to introduce the flexibility of the protein binding site as well as that of the ligand by utilizing the generalized REST (gREST) method (37). The approach, which we call gREST/REUS, realizes extensive sampling of binding and unbinding events and provides converged free-energy landscapes, which allows us to characterize binding poses on multiple binding pathways with unprecedented accuracy.

We apply the method to investigate the binding of PP1 (ATP-competitive inhibitor) to c-Src kinase, a key signaling kinase in the cancer process (38, 39). A previous microsecond timescale unbiased MD simulation correctly predicted the structure of c-Src kinase complexed with either PP1 or dasatinib as observed in the X-ray crystal structures (17). The simulation shows that PP1 resides for a long time in the vicinity of the N-lobe before binding through a water-separated intermediate. A subsequent free-energy calculation shows that desolvation of the binding pocket is the main contributor to the free-energy barrier (40). More recently, a metadynamics-based unbinding simulation gave further insight into the protein–water coupled dasatinib binding (24). The study reports the k_off value and relates it to cleavages of the evolutionally conserved Lys-Glu salt bridge and the dasatinib-hinge hydrogen bonds. In this work, we characterize the structures and interactions of multiple binding poses, transient intermediates, encounter complexes, and pathways connecting them, on the free-energy landscapes. The calculated energetics and kinetics agree with experiments as well as with previous computations. We integrate those findings and propose a parallel binding model. We highlight the role of G-loop residues distant from the catalyst core at the early stage of the binding process, i.e., the formation of encounter complexes, which was unresolved by a mutagenesis experiment and X-ray crystal structures (10). We believe that this work provides an effective strategy to optimize drug efficacy with prolonged target residence times.

Results

Efficiency of gREST/REUS Simulation.

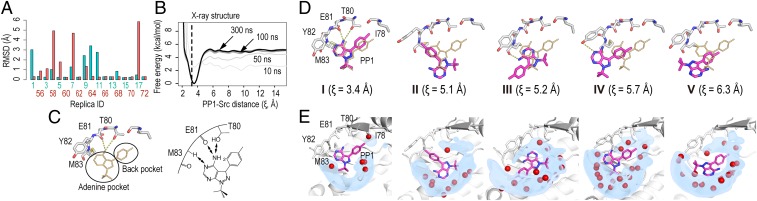
The details of gREST/REUS simulation are described in Materials and Methods and SI Appendix. In brief, gREST/REUS simulation conducts replica exchanges in 2 dimensions: exchanges of the PP1-Src distance umbrella potentials (REUS dimension), and exchanges of solute temperatures (gREST dimension). The solute is defined as the dihedral angle and the nonbonded energy terms of both PP1 and 10 binding site residues, based on the X-ray crystal structure (Fig. 1 and SI Appendix, Fig. S1). The current choice of the solute enhances the flexibility of protein binding site residues (SI Appendix, Table S1) and significantly increases the chance of binding events to occur. In 78% of the replicas, the minimum heavy atoms rsmd between the ligand PP1 and the X-ray crystal structure is <1 Å (Fig. 2A, SI Appendix, Table S2 and Figs. S2–S6, and Movies S1 and S2). Simulating 100 binding and unbinding events, obtaining convergence of the protein structure (SI Appendix, Fig. S7), we are able to characterize the bound state and transient intermediates on the statistically converged free-energy landscapes (Fig. 2B).

Fig. 2.

Structures and hydration of bound states. (A) Minimum values of heavy atoms rmsd of the ligand PP1 from the X-ray structure (1QCF) for selected replicas (replica indexes of 1 to 18 and 55 to 72). (B) Free-energy profiles at 310 K along the PP1-Src distance (ξ). The PP1-Src distance (ξ) in the X-ray structure (1QCF, ξ = 3.25 Å) is shown as a dotted line. (C) The X-ray structure with 2 dominant pockets: the adenine pocket for hydrogen bonding with the hinge region and the back pocket for hydrophobic interaction. The hydrogen bonds between PP1 and hinge residues are shown by the yellow dotted line. (D) The bound (I) and semibound (II–V) poses obtained from the simulation. PP1 in the X-ray structure is shown in gold for comparison. The hydrogen bonds between PP1 and hinge residues are preserved in pose I, but not in the semibound poses. (E) Volume map representation of water distribution (isosurface at 20% occupancy) around the binding pocket. Red spheres in the bound (I) and the semibound (II–V) poses, respectively, represent water molecules in the X-ray structure and from the simulation. The poses I, II, III, IV, and V, respectively, correspond to B^zz, B^pp, B^pz, B^zz*, and B^zp in Figs. 3 and 4.

Multiple Binding Poses of the Inhibitor and Water Molecules.

First we identify multiple binding poses by standard k-means clustering analysis, which uses Euclidean distance function to classify the structures in the trajectory data at 310 K into a predefined number of clusters (10 in the present study) (SI Appendix, Fig. S8). In Fig. 2 C and D, we show 5 representative poses of the bound region (ξ < 6 Å). The major pose I, which dominates the bound region of ξ < 4 Å, is in excellent agreement with the X-ray structure (PDBID: 1QCF) (41). PP1 occupies both the adenine and the back pockets and forms highly conserved hydrogen bonds with the hinge residues: 1 with the side chain of the gatekeeper residue (Thr80), and an additional 2 with the main chain of the hinge residues (Glu81and Met83) (8). We also find 4 semibound poses in the region of ξ = 5 ∼ 6 Å, which are not resolved in the X-ray structure. Pose IV has the same PP1 orientation as pose I, while the other poses (II, III, and V) have different orientations. In the semibound poses, PP1 occupies only the adenine pocket, and the hydrogen bonds with the hinge residues are mostly absent.

The volmap feature in the Visual Molecular Dynamics (VMD) software (isosurface at 20% occupancy) provides water distribution in the binding pocket in each pose (Fig. 2E) (42). The water distribution in pose I overlaps with water positions in the X-ray structure. In the other poses, a layer of water molecules in the back pocket separates PP1 and the binding site residues and breaks the hydrogen bonds with Thr80 and Glu81. The semibound pose IV agrees well with a prebound pose found in the earlier conventional MD simulation (17). The previous free energy analysis shows that desolvation of the binding pocket mainly contributes to the free-energy barrier for the dasatinib binding to the Src kinase (40). Given that the water molecules deep inside the pocket are absent only in the pose I, desolvation of the pocket likely relates to the molecular orientation of the inhibitor.

Encounter Complexes in Parallel Pathways.

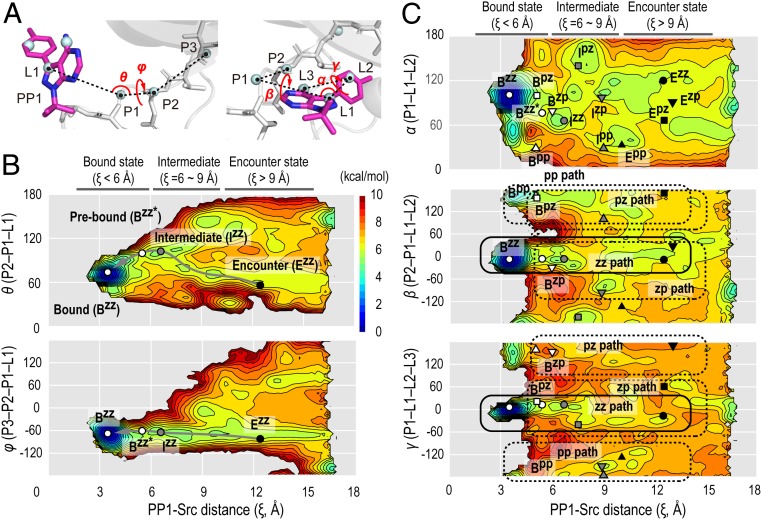
We can confidently characterize the binding pathways with multiple intermediates, including encounter complexes, by constructing free-energy landscapes from the simulation data. For this purpose, a set of 2D free-energy landscapes was constructed along the reaction coordinate, chosen as the PP1-Src distance (ξ), and either the PP1 position or orientation with respect to the protein, defined using 6 anchor atoms (P1, P2, and P3 from the protein and L1, L2, and L3 from PP1). For example, P1 is defined as the center of mass (COM) of the protein backbone heavy atoms of the residue closest to the COM of the protein (SI Appendix for details). The position and orientation of PP1 are defined by polar angles, θ (P2-P1-L1) and φ (P3-P2-P1-L1), and Euler angles, α (P1-L1-L2), β (P2-P1-L1-L2), and γ (P1-L1-L2-L3), respectively (Fig. 3A). The free-energy landscapes along the PP1-Src distance (ξ) and position, (θ, ξ) and (φ, ξ), are smooth and the predominant binding pathway is well defined (Fig. 3B). In the (θ, ξ) landscape, we also find a secondary path originating from the large θ value (∼120°), in addition to the dominant path from the small θ value (∼60°). On the contrary, 3 landscapes along the PP1-Src distance (ξ) and orientation, (α/β/γ, ξ), are relatively rugged (Fig. 3C). This means that PP1 enters the pocket through a unique azimuth angle but in various molecular orientations.

Fig. 3.

Free-energy landscapes along PP1 position and orientation. (A) Polar angles, θ (P2-P1-L1) and φ (P3-P2-P1-L1) designating PP1 position (Left) and Euler angles, α (P1-L1-L2), β (P2-P1-L1-L2), and γ (P1-L1-L2-L3), designating PP1 orientation (Right). (B) Free-energy landscapes at 310 K along the PP1-Src distance (ξ) and polar angles (θ and φ) for the gREST/REUS simulation. (C) Similar landscapes as in B for Euler angles (α, β, and γ). Positions of representative structures in each state from the k-means clustering analysis are marked on the landscapes (white: bound state; gray: intermediate; black: encounter state). The pathway to the canonical binding pose (E^zz → B^zz) is indicated by the gray arrow line. The plausible parallel binding pathways to multiple poses are indicated by solid and dotted frames.

In order to characterize the binding pathways, we classify the bound poses in Fig. 2D (Poses I ∼ V) by PP1 orientation: B^zz (around β = 0° and γ = 0°), B^zp (around β = 0° and γ = 180°), B^pz (around β = 180° and γ = 0°), and B^pp (around β = 180° and γ = 180°) (SI Appendix, Fig. S9). Given that pose IV, having the same orientation as pose I, is an intermediate toward pose I, there are actually 4 distinctive poses (thus we denote pose IV as B^zz*). In the free-energy landscapes in Fig. 3C, the canonical pose B^zz (= pose I) is located around ξ = 3 Å, whereas the semibound poses (B^zp, B^pz, and B^pp) and the intermediate pose (B^zz*) are found in the region of ξ = 5 ∼ 6 Å. Because of the energy barriers dividing these poses in Fig. 3C, multiple poses may not be directly exchangeable. To confirm this, we perform independent microsecond-long conventional MD simulations (total 15 μs), where PP1 is bound after 4 μs and 3.2 μs in 2 of the 3 simulations (SI Appendix). The analysis of simulation trajectories supports that the multiple poses are not mutually exchanged in the bound region. For example, the trajectory leading to the semibound pose, B^pz, dissociates without changing to other poses after reaching the bound state (SI Appendix, Fig. S10). The plausible parallel binding pathways to multiple poses are indicated in the free-energy landscapes in Fig. 3C. We also find distinct pathways to multiple poses in the 3D probability distribution (Movies S3 and S4). The projection of free-energy landscapes onto the pairs of reaction coordinates is useful to understand molecular mechanisms underlying the parallel binding pathways. The combined kinetic network models and flux analysis could help to rigorously characterize the pathways based on kinetic flux (43), although more extensive conformational sampling is necessary. Parallel binding pathways are observed for the ligand in other proteins, such as p38 MAP kinase (28), bromodomain (20), and LAO protein (22) and may be a general feature of the ligand binding process (44).

Using the k-means clustering analysis of the regions excluding the bound region (ξ > 6 Å) (SI Appendix, Fig. S8), we extract the representative intermediate and encounter complex structures along the pathways to different poses, and their positions are superposed on the free-energy landscapes in Fig. 3C. Multiple bound states (B^zz, B^zp, B^pz, and B^pp) are connected only through their own encounter states. The 4 parallel binding pathways are sketched in Fig. 4A. In 3 of them, including the major pathway (E^zz → B^zz), PP1 enters the binding pocket from the G-loop side. In the E^pz → B^pz pathway on the contrary, PP1 directly accesses the hinge region. The latter corresponds to the path approaching from the large θ value (∼120°) in the free-energy landscape for the PP1 position (Fig. 3B).

Fig. 4.

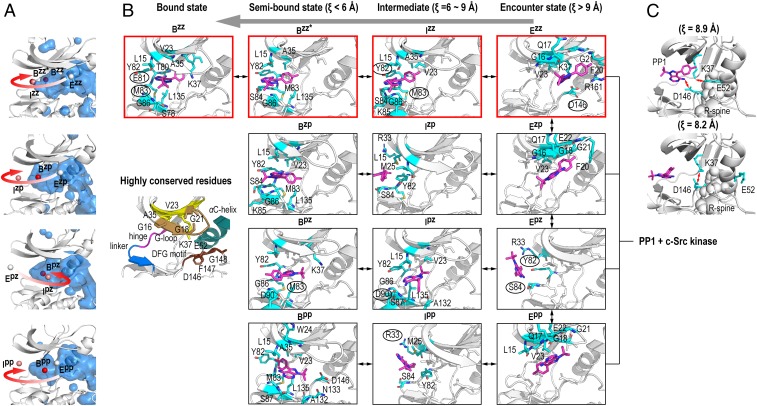
Parallel binding modes of PP1-Src. (A) Position of the COM of PP1 in each state for different pathways. The binding site cavity is shown in blue. (B) Representative structures in each state obtained from the k-means clustering analysis for each binding pathway. Residues within 4 Å from PP1 are highlighted in cyan. The residues interacting with PP1, as obtained from LIGPLOT analysis, are labeled (plane for hydrophobic and circled for hydrogen bonded interactions). The major pathway leading to the canonical pose (E^zz → B^zz) is highlighted with the red border. Highly conserved residues in the binding pocket (8) are shown (Left Middle). (C) Two representative structures in the transition state region (ξ = 8 Å ∼ 9 Å) along the main pathway (E^zz → B^zz) obtained from the k-means clustering analysis.

Fig. 4B illustrates the binding site interactions along the pathways. In the encounter complexes (E^zz, E^zp, and E^pp), PP1 interacts with the highly conserved GxGxxG motif in the G-loop (8). We find an additional hydrogen bond with the side chain of Asp146 of the conserved Asp-Phe-Gly (DFG) motif in E^zz, which likely fixes PP1 to the canonical pose orientation. Only in E^pz, PP1 directly accesses the pocket by forming hydrogen bonds with the hinge residues (the side chain of Tyr82 and the main chain of Ser84). In a subsequent step toward the canonical pose (E^zz → B^zz), PP1–G-loop interactions are replaced with hydrogen bonds to the hinge residues (the side chain of Tyr82 and the main chain of Met83), where Val23 appears to assist in retaining PP1 inside the pocket. Accompanied with coupled desolvation of the binding pocket, these hydrogen bonds finally rearrange to produce the well-conserved hydrogen bonds with the gatekeeper (Thr80) and the hinge residues (Glu81and Met83), stabilizing the canonical bound state B^zz (= pose I). An interaction switch from PP1–G-loop to PP1–hinge residues is observed in the other pathways (E^zp → B^zp and E^pp → B^pp), but these PP1 orientations preclude hydrogen bond formation. Hence, multiple bound states are commonly stabilized by interaction with the hinge residues, but the interaction mechanism is different. Evidently, the G-loop residues play a major role in stabilizing the encounter complexes. The G-loop displays a remarkably high flexibility, but its fluctuations are largely suppressed by the formation of encounter complexes (SI Appendix, Fig. S11). In addition, upon going from the encounter complex to the bound state, Phe20 reorients to fill the space originally occupied by PP1 (SI Appendix, Fig. S12). Thus, the G-loop also contributes to the secondary stabilization of the bound state.

Along the main pathway (E^zz → B^zz), we find the highest free-energy region in between E^zz and I^zz (ξ = 8 ∼ 9 Å). We create an ensemble of the transition state structures by extracting 1,600 structures that satisfy the following conditions from the simulation trajectory at 310 K: 8 Å < ξ < 9 Å, 60° < θ < 100°, 60° < α < 120°, 60° < β < 100°, and 60° < γ < 100°. The k-means clustering, with the input number of clusters equal to 5, provides 2 representative structures at ξ ∼ 8.9 Å (77.1%) and ξ ∼ 8.2 Å (22.9%) (Fig. 4C). In the former, the conserved Lys37-Glu52 salt bridge is maintained (Lys37:Cδ − Glu52:Cε distance is 4.4 Å), while in the latter, the salt bridge is broken and instead Lys37 forms a hydrogen bond with Asp146, releasing PP1. Concomitantly, the αC-helix transiently rotates outward, opening the access to the binding pocket. This feature of the transition state region is consistent with the molecular switch mechanism proposed for the dasatinib-Src kinase binding (24). The mutagenesis experiment shows that the Src residues stabilizing the inactive αC-helix-out conformation is sensitive to the inhibitor binding (10). The coupled salt bridge and αC-helix motion is a key feature of the transition state for inhibitor-kinase binding.

Binding Energy and Kinetics.

The present simulation describes half of the binding process: i.e., from the encounter to the bound state (intrusion into the binding pocket). The corresponding free-energy change, ΔG^intrusion, is −3.6 kcal/mol, obtained by integrating the bound (ξ = 2 ∼ 10 Å) and unbound (ξ = 10 ∼ 16 Å) regions of the free-energy profile in Fig. 2B and taking their ratio. The value of ΔG^intrusion displays the increase to −4.3 kcal/mol when increasing the boundary distance up to ξ = 14 Å (bound region: ξ = 2 ∼ 14 Å, unbound region: ξ = 14 ∼ 16 Å). The estimated ΔG^intrusion corresponds to 2,900 μM, which is significantly larger than the experimental IC₅₀ (170 nM) (45). An independent free-energy perturbation calculation produces a binding free energy (ΔG^bind) value of −8.6 kcal/mol (K_d = 808 nM), which reproduces the experimental IC₅₀ to a reasonable extent (SI Appendix, Table S3). The difference between ΔG^bind and ΔG^intrusion is about −5 kcal/mol, which corresponds to the free-energy change associated with the encounter complex formation. The result is consistent with the finding on Gleevec for which the physical binding step contributes only micromolar affinities (−6.5 kcal/mol) for both Abl and Src (12). However, the PP1 is small and its intrusion is accompanied by subtle changes in the binding site: the transient breaking of the Lys37-Glu52 salt bridge (Fig. 4C) and the reorientation of Phe20 (SI Appendix, Fig. S12). This may contrast to the Gleevec-Abl kinase binding for which a large conformational change (a slow induced-fit process) is suggested (12).

To link with binding kinetics, we analyzed the data of independently performed microsecond-long conventional MD simulations (SI Appendix). The estimated k_on value is 4.6 μM⁻¹ agreeing with the previous computational estimate (17) and the experimental value (∼5 μM⁻¹) (46). This value, combined with the calculated K_d (808 nM) produces a k_off value of 3.7 s⁻¹ using the K_d = k_off/k_on relation, resulting in a residence time (1/k_off) of 0.3 s. The reported residence time for dasatinib-Src binding, with a dissociation constant of 11 nM, is 21 ± 10 s as estimated by simulation (24) and 18 s to 900 s by experiments (47, 48). Considering that the binding of PP1 to the Src kinase is weaker than that of dasatinib, the estimated residence time is reasonable.

Discussion

Precision Drug-Target Binding Simulations.

Drug-target binding simulations have evolved from predicting binding affinities to mapping binding pathways and kinetics. The present gREST/REUS simulations realize multiple binding and unbinding events, achieved by enhanced flexibilities of the inhibitor and the protein binding site. The simulations display faster statistical convergence than in the original method, REST/REUS and provide reliable free-energy landscapes for understanding molecular mechanisms. Currently, simulations are limited to sampling from the encounter region to the bound state, and thus direct estimation of kinetic parameters is not feasible. However, the reversible sampling of the binding and unbinding events using gREST/REUS serves as the basis for accurate estimation of thermodynamics and kinetics, complementary with other methods. For example, the gREST/REUS may be integrated with Markov state modeling (MSM) with the transition-based reweighting analysis method (TRAM) (49, 50) to significantly improve the efficiency of estimating drug-target unbinding kinetics. Alternatively, gREST/REUS simulations can be combined with the Brownian dynamics approach (51, 52) or multiple independent MD, such as Parallel Cascade Selection Molecular Dynamics (19) to provide both an atomic level description of the binding pathway and kinetic parameters at high accuracy. The present 2D replica exchange approach requires large computational resources, which prevent routine usages. For a relatively fast binding process, 1-dimensional gREST may be successful. Another possibility is to replace the gREST with a nonreplica type enhanced sampling method (53–55), maintaining sampling efficiency while reducing the total number of replicas. The simplicity of the present scheme could serve as a basis for future complementary approaches using various types of enhanced sampling methods for precision drug-target binding simulations.

Encounter Complexes with G-Loop.

Traditional drug compound design has relied on the structures and interactions at the bound state resolved by X-ray crystallography. The analysis of free-energy landscapes illuminates the roles of regulatory residues in the binding process, which are not obtainable from the bound state structure. Here, we succeeded in predicting the encounter complexes on the multiple binding pathways for PP1-Src binding. The formation of an encounter complex is generally considered as a key step guiding the ligand toward a final bound state (56), while it is difficult to observe and characterize the transient encounter complexes experimentally (57). Our simulation shows that the G-loop grabs PP1 by forming encounter complexes, and the interaction between the G-loop and PP1 decides whether to enter the pocket in the right orientation. In previous studies, the interaction with the G-loop was found to modulate the inhibitor selectivity (10, 11, 58, 59). The mutagenesis experiment shows the combined contribution of the G-loop and other regulatory residues to the observed selectivity (10). Our simulation shows that the conserved G-loop is preferentially responsible for the initial uptake of the inhibitor and the regulation of subsequent bindings. This mechanism is applicable to several inhibitor-kinase bindings. Whether the encounter states have some influence on the binding selectivity or not is an open question for future study.

Implication for Design.

The encounter complexes and parallel binding pathways characterized in this work can provide new perspectives for the inhibitor design. Our results suggest that the modulation of encounter complexes can be an effective strategy for controlling the inhibitor binding, in addition to control of the rate-limiting step thorough the conserved salt bridge (24). The stabilization of encounter complexes can extend the residence time (lower the k_off) without affecting the association rate (k_on). The enhanced stability of the encounter complex may also retard the dissociation from the semibound poses and can help extend the residence time. The validity of this idea can be seen in the recently designed Mps1/TTK kinase inhibitors, where the shift of the G-loop position is related to the slow binding kinetics (60). It is likely that the G-loop traps the inhibitor at an encounter state, resulting in the observed slow kinetics. Conversely, by designing the compound so as to destabilize the encounter complexes against off-target proteins, it is possible to effectively increase the binding to the target protein. Thus, the possibility of inhibitor design would be widened by targeting the encounter complexes. The encounter complexes characterized in this work are only those directly leading to the bound states, but in fact, the inhibitor can form encounter complexes at multiple sites on the protein surface (17). Further analysis of inhibitor dynamics including these encounter complexes, using methods such as MSM, may provide yet another strategy for extending the residence time. Our simulation predicts the existence of semibound poses that are not resolved in the X-ray crystal structure. The interactions with the surrounding residues of the semibound poses are different from that of the canonical pose. It would be possible to control the inhibitor binding by stabilizing/blocking the semibound poses. As the binding process becomes explored, the possibility of ATP-competitive inhibitor design will greatly expand and help to overcome the difficulty in the traditional design based on the X-ray crystal structures.

Materials and Methods

MD Simulation.

The initial configuration of the PP1-Src complex was constructed using the X-ray structures of the unphosphorylated c-Src in active conformation (PDBID: 1Y57) (61) and of the autoinhibited form of Hck in complex with PP1 (PDBID: 1QCF) (41). The PP1-Src complex was solvated by water molecules and neutralized by 6 sodium cations. All simulations were performed using a development version of the GENESIS program package (62, 63). We used the AMBER ff99SB-ILDN (64, 65) and TIP3P (66) parameters for the protein and water molecules, respectively. The ligand parameters were obtained by using GAFF with AM1-BCC (67).

Two-Dimensional gREST/REUS Simulation.

We defined the solute region in gREST as the dihedral angle and nonbonded energy terms of an inhibitor PP1 and 10 binding site residues, based on the X-ray crystal structure. Eight replicas were used to cover the solute temperature range of 310 ∼ 3,100 K (gREST dimension). The reaction coordinate (ξ) of the umbrella sampling simulation (REUS dimension) was taken as the distance between COMs of PP1 and the backbone heavy atoms of 2 binding site residues (Ala35 and Leu135). Eighteen replicas were used to cover the ξ values in the range of 3.0 Å ∼ 15.0 Å. The total number of replicas in gREST/REUS simulation is 18 × 8 = 144. Replica exchange was attempted every 2 ps alternatively for the REUS and gREST dimensions. Following 1 ns of equilibration run for each replica, gREST/REUS for 300 ns per replica (43.2 μs in total) was performed for the purpose of analyzing the PP1-Src binding.

Additional details are described in SI Appendix.