Prediction of Tissue-Plasma Partition Coefficients Using Microsomal Partitioning: Incorporation into Physiologically based Pharmacokinetic Models and Steady-State Volume of Distribution Predictions

Abstract

Drug distribution is a necessary component of models to predict human pharmacokinetics. A new membrane-based tissue-plasma partition coefficient (K_p) method (K_p,mem) to predict unbound tissue to plasma partition coefficients (K_pu) was developed using in vitro membrane partitioning [fraction unbound in microsomes (f_um)], plasma protein binding, and log P. The resulting K_p values were used in a physiologically based pharmacokinetic (PBPK) model to predict the steady-state volume of distribution (V_ss) and concentration-time (C-t) profiles for 19 drugs. These results were compared with K_p predictions using a standard method [the differential phospholipid K_p prediction method (K_p,dPL)], which differentiates between acidic and neutral phospholipids. The K_p,mem method was parameterized using published rat K_pu data and tissue lipid composition. The K_pu values were well predicted with R² = 0.8. When used in a PBPK model, the V_ss predictions were within 2-fold error for 12 of 19 drugs for K_p,mem versus 11 of 19 forK_p,dPL. With one outlier removed for K_p,mem and two for K_p,dPL, the V_ss predictions for R² were 0.80 and 0.79 for the K_p,mem and K_p,dPL methods, respectively. The C-t profiles were also predicted and compared. Overall, the K_p,mem method predicted the V_ss and C-t profiles equally or better than the K_p,dPL method. An advantage of using f_um to parameterize membrane partitioning is that f_um data are used for clearance prediction and are, therefore, generated early in the discovery/development process. Also, the method provides a mechanistically sound basis for membrane partitioning and permeability for further improving PBPK models.

SIGNIFICANCE STATEMENT

A new method to predict tissue-plasma partition coefficients was developed. The method provides a more mechanistic basis to model membrane partitioning.

Introduction

The volume of distribution and clearance equally determine the half-life of a drug. The steady-state volume of distribution (V_ss) can be predicted using empirical methods (Obach et al., 1997), computational approaches (Ghafourian et al., 2004; Lombardo et al., 2006; Zhivkova and Doytchinova, 2012), physiologic equations (Oie and Tozer, 1979; Lombardo et al., 2004; Korzekwa and Nagar, 2017a), and tissue:plasma partition coefficients (K_p). The K_p prediction methods are widely used since they describe the distribution in physiologically based pharmacokinetic (PBPK) models. While some methods require an in vivo component (Arundel, 1997; Björkman, 2002; Jansson et al., 2008; Poulin and Theil, 2009), others use more readily available in vitro inputs.

Several factors influence drug distribution, including partitioning into membranes and other lipids, binding to proteins (primarily plasma proteins), pH partitioning (e.g., lysosomes), transporters, and membrane permeability. Most models represent tissue interactions with in vitro surrogates. The Poulin and Krishnan (1995) model originally described phospholipid partitioning with the octanol:water partition coefficient (P) and assumed phospholipid composition to be represented by 30% octanol and 70% water. They developed K_p prediction equations that included an additional surrogate for neutral lipid partitioning in adipose tissue (Poulin and Theil, 2000; Poulin et al., 2001), which was modified by Berezhkovskiy (2004). Rodgers and Rowland (2006) developed two equations for prediction of unbound K_p (K_pu): one for acids, neutrals, and weak bases, and another for moderate-to-strong bases (Rodgers et al., 2005). Drug partitioning into erythrocytes was used to parameterize the interaction of bases with acidic phospholipids (APs). It was assumed that ionized bases interact only with APs, while uncharged molecules interact only with neutral phospholipids (Rodgers et al., 2005; Rodgers and Rowland, 2006).

In most currently used composition-based models, log P is used to model the phospholipid partitioning (0.3P). A shortcoming of using log P to represent phospholipid partitioning is the lack of orientation-specific interactions with phospholipid membranes (Balaz, 2009; Nagar and Korzekwa, 2012, 2017). Additionally, both neutral and ionized bases are known to interact with all phospholipids, and not just net-neutral and net-acidic phospholipids, respectively. Therefore, current methods to calculate K_p appear to be based on mechanistically unsound assumptions. Previously, we used microsomal partitioning [fraction unbound in microsomes (f_um)] instead of log P to parameterize phospholipid partitioning in a V_ss model (Korzekwa and Nagar, 2017a). Partitioning into microsomes (unsorted phospholipid vesicles) is used extensively in clearance predictions and can be determined experimentally or predicted (Austin et al., 2002; Hallifax and Houston, 2006; Poulin and Haddad, 2011; Nagar and Korzekwa, 2017). A benefit of using f_um to represent phospholipid partitioning is that it measures interactions with all phospholipids for both charged and uncharged species.

Previous studies have compared different K_p prediction methods and their ability to predict both tissue K_p and/or V_ss (De Buck et al., 2007; Poulin and Theil, 2009; Jones et al., 2011; Graham et al., 2012; Zou et al., 2012; Chan et al., 2018). These studies came to different conclusions on the most accurate K_p model, which was primarily dependent on the drug data set used (De Buck et al., 2007; Graham et al., 2012). Graham et al. (2012) showed that the Rodgers et al. (2005) method was able to better predict K_p and V_ss for different classes of drugs than other composition-based models. The Poulin and Theil (2009) method led to good V_ss predictions, but required in vivo data (K_pu muscle) (Graham et al., 2012). More recently, Chan et al. (2018) compared the ability of composition-based K_p models and preclinical extrapolation to predict V_ss. Composition-based models predicted V_ss with accuracy similar to preclinical extrapolation. They noted that the Rodgers method was able to predict V_ss well for drugs with log P values less than 3, and that many drugs with large errors in V_ss for composition-based models also had errors in preclinical extrapolation (Chan et al., 2018).

This report evaluates a model to predict K_p using f_um to represent membrane partitioning. Plasma protein binding and microsomal partitioning values were determined experimentally for 19 drugs. Tissue K_p values were calculated for each compound using a differential phospholipid K_p prediction method (K_p,dPL) (Rodgers et al., 2005; Rodgers and Rowland, 2006), as well as a method that uses f_um to parameterize membrane partitioning [the membrane-based K_p prediction method (K_p,mem)]. Simulations were run and their ability to predict V_ss and concentration-time (C-t) profiles was determined. More mechanistically sound assumptions for K_pu will be required when expanding current perfusion-limited PBPK models to include explicit membrane partitioning and permeability. Models to predict K_pu bases on experimental partitioning into membranes may allow a facile transition to models that limit permeability with explicit membrane compartments (Nagar et al., 2014).

Materials and Methods

Materials.

A Harvard Apparatus (Holliston, MA) 96-well equilibrium dialyzer and single-plate Harvard Apparatus plate rotator were used for equilibrium dialysis experiments. Human plasma was obtained from US Biologic (Salem, MA) and Innovative Research Inc. (Novi, MI). Rat liver microsomes were obtained from BD Biosciences (San Jose, CA) and Corning Life Sciences (Tewksbury, MA). Warfarin, fluconazole, glyburide (glybenclamide), ketoprofen, fenofibrate, +/cis-diltiazem hydrochloride, +/− verapamil hydrochloride, caffeine, betaxolol hydrochloride, DMSO, nicardipine hydrochloride, metoprolol tartrate, felodipine, and nafcillin sodium were obtained from Sigma Aldrich (St. Louis, MO). Quinidine gluconate, formic acid, acetonitrile, and diphenhydramine hydrochloride were obtained from Fisher Scientific (Norristown, PA). Mibefradil hydrochloride was obtained from Cayman Chemical Company (Ann Arbor, MI). Diclofenac sodium was obtained from Calbiochem (Burlington, MA). Fenofibric acid was obtained from Kano Laboratories (Nashville, TN). One milligram per milliliter solutions of phenytoin, diazepam, and midazolam in methanol were obtained from Cerilliant (a Sigma Aldrich company). The 100 mM PBS and 0.3 mM MgCl₂ dialysis buffer was composed of magnesium hydrochloride hexahydrate (Fisher Scientific), potassium phosphate monobasic (Sigma Aldrich), and potassium phosphate dibasic (Fisher Scientific). An Agilent 1100 HPLC and API 4000 mass spectrometer and Agilent 1100 HPLC and API 4000 Q-Trip mass spectrometer were used to determine the concentrations for equilibrium dialysis. Mathematica version 11.0 (Wolfram, Champaign, IL) was used for all compartmental modeling and simulations. Literature data from plots were digitized using Engauge Plot Digitizer version 10.4 (GitHub, San Francisco, CA).

Probe Drug Selection and Data Collection.

A diverse set of drugs made up of acids, bases, and neutrals was selected to compare the prediction methods (Table 1). Drugs were considered neutral when primarily uncharged at physiologic pH (7.4). Unless noted otherwise, the pK_a values of acids (pK_a,a) and bases (pK_a,b) for neutrals were set at 14 and 1, respectively. Any significant ionized and neutral fraction was considered by both methods. The probe drugs were selected based on the availability of literature intravenous pharmacokinetics data, as well as drug-specific parameters. Average experimental intravenous bolus and/or infusion C-t profiles for 19 drug studies were collected from the literature. If the data were represented as graphical C-t profiles, the plots were digitized. When average subject weight was available, simulations were conducted to reproduce the observed V_ss for that average weight. The observed clearance and the steady-state volume of distribution were determined by compartmental analysis using standard equations with Mathematica. Specifically, one- to three-compartment models were evaluated to generate the C-t profiles from the experimental data. Experimental clearance and V_ss values were determined from these compartmental models. The best model for the experimental data was determined by the corrected Akaike information criterion values (Akaike, 1974) and residual plots. For all drugs, microrate constants were well defined and use of noncompartmental analysis was not required. Experimental clearance values were assumed for all further modeling efforts and experimental V_ss values were compared with predicted values.

TABLE 1.

Pharmacokinetic parameters of test drugs

Test Drug	Class	Type	Number of Subjects	Weight	Dose	Duration	Number of Points	Vss	CL	Reference
				kg	mg	min		l	l/h
Betaxolol	B	Infusion	n = 10	73.6	8.94	30	17	360	11	Ludden et al., 1988
Diltiazem	B	Infusion	n = 12	63	15	30	13	306	97	Hermann et al., 1983
Diphenhydramine	B	Bolus	n = 8	98.0	56	N/A	12	788	43	Scavone et al., 1990
Metoprolol	B	Infusion	n = 5	66	3.9	10	20	274	59	Regårdh et al., 1974
Mibefradil	B	Infusion	n = 6	70a	20	30	16	187	17	Clozel et al., 1991
Nicardipine	B	Bolus	n = 6b	67.0	10	N/A	12	62	76	Campbell et al., 1985
Quinidine	B	Infusion	n = 12b	65.3	244	22	12	227	18.5	Ueda et al., 1976
Verapamil	B	Infusion	n = 20	70a	10	5	15	266	49	McAllister and Kirsten, 1982
Caffeine	N	Infusion	n = 10	79.5	350	30	17	42.8	5.2	Blanchard and Sawers, 1983
Diazepam	N	Infusion	n = 24	78.1	5	1	21	89.5	1.33	Agarwal et al., 2013
Felodipine	N	Infusion	n = 10	74	2.5	30	22	320	41.7	Edgar et al., 1985
Fluconazole	N	Infusion	n = 6	70a	50	N/A	13	59.3	1.25	Ripa et al., 1993
Midazolam	N	Bolus	n = 6	67.6	10	N/A	15	51.2	18	Heizmann et al., 1983
Phenytoin	N	Infusion	n = 6	78.1	275	6	15	38.8	1.76	Gugler et al., 1976
Diclofenac	A	Infusion	n = 6	65	46.5	2	15	9.23	17.6	Willis et al., 1980
Glyburide	A	Infusion	n = 10	77.8	2	60	19	11.78	4.88	Debruyne et al., 1987
Ketoprofen	A	Bolus	n = 7	70a	100	N/A	12	9.9	5.02	Debruyne et al., 1987
Nafcillin	A	Infusion	n = 6	70a	475	7	9	20.4	33.9	Waller et al., 1982
Warfarin	A	Bolus	n = 6	66.8	100	N/A	8	7.66	0.179	O’Reilly et al., 1971

A, acids; B, bases; N, neutral; CL, clearance.

^aIndividual weights not provided and 70 kg assumed.

^bIndividual C-t not provided. C-t profile simulated from average parameters.

Literature physiologic data were used for K_p predictions and PBPK modeling (Brown et al., 1997; Poulin and Theil, 2002; Fenneteau et al., 2010; Ye et al., 2016). For drug-specific parameters [log P, pK_a, and blood to plasma (BP)] (Table 2), experimental values from the literature were preferred over calculated/predicted values, and if more than one experimental value was found, then the experimental values were averaged. Human BP values could not be found for betaxolol and nafcillin. For betaxolol, the values of the fraction unbound in plasma (f_up) were similar for rat and human; therefore, the rat BP value of 2.0 was used. For nafcillin, a value of 0.55 (1-hematocrit) was used, which is the BP ratio of similar compounds in humans (Greene et al., 1978). Also, this will not affect V_ss predictions since BP is not included in the K_p equations for acids. Protein binding was experimentally determined for all compounds (Table 2), with the exception of caffeine due to caffeine contamination in all plasma samples. A caffeine f_up value of 0.72 was determined by averaging values found in the literature.

TABLE 2.

Drug-specific parameters

Compound	Class	fup (n = 4)a	fum (n = 4)a	Log P	pKa,a	pKa,b	BP	Log Dvo	CL	Reference
									l/h
Betaxolol	B	0.50 (12%)	0.77 (3%)	2.81	14	9.4	2b	1.78	10.2	Riddell et al., 1987; Recanatini, 1992; Rodgers and Rowland, 2007
Diltiazem	B	0.26 (8%)	0.48 (2%)	2.7	14	7.7	1	1.88	97.5	Rekker and Mannhold, 1992; Obach, 1999; Ishihama et al., 2002
Diphenhydramine	B	0.44 (4%)	0.84 (4%)	3.27	14	8.98	0.74	2.30	43	Albert et al., 1975; Sangster, 1994; Hansch et al., 1995; Obach, 1999
Metoprolol	B	0.87 (17%)	0.80 (3%)	1.88	14	9.7	1.14	0.746	58.8	Hansch et al., 1995; Rodgers and Rowland, 2007
Mibefradil	B	0.031 (11%)	0.034 (15%)	3.07	14	10.2	0.64	2.07	15.5	Welker et al., 1998; Nagar and Korzekwa, 2017
Nicardipine	B	0.0024 (7%)	0.039 (12%)	3.82	14	8.6	0.71	2.90	31.2	Sangster, 1993; Rodgers and Rowland, 2007
Quinidine	B	0.15 (8%)	0.815 (10%)	3.52	14	8.94	0.92	2.07	14	Sangster, 1994; Obach, 1999; Nagar and Korzekwa, 2017
Verapamil	B	0.088 (20%)	0.37 (19%)	3.79	14	8.92	0.74	2.88	49	Sangster, 1994; Hansch et al., 1995; Robinson and Mehvar, 1996; Obach, 1999
Caffeine	N	0.72c	0.98 (6%)	−0.07	14	1.04	1.01	−1.43	5.2	Hansch et al., 1995; Rodgers and Rowland, 2007
Diazepam	N	0.012 (9%)	0.74 (4%)	2.82	14	3.4	0.64	1.79	1.33	Maguire et al., 1980; Sangster, 1993; O’Neil, 2006
Felodipine	N	0.0017 (12%)	0.023 (27%)	3.86	14	5.07	0.7	2.95	41.7	Diez et al., 1991; Uchimura et al., 2010; Pandey et al., 2013
Fluconazole	N	0.93 (14%)	0.94 (14%)	0.8	14	1.77	1	−0.79	1.25	Debruyne et al., 1987; Debruyne, 1997; Rodgers and Rowland, 2007
Midazolam	N	0.033 (4%)	0.71 (4%)	3.15	14	6.01	0.53	2.16	18	Heizmann et al., 1983; Rodgers and Rowland, 2007
Phenytoin	N	0.18 (7%)	0.83 (3%)	2.21	8.32	1	0.61	1.11	1.61	Stella et al., 1998; Brittain, 2007; Uchimura et al., 2010
Diclofenac	A	0.0014 (18%)	0.78 (4%)	4.51	4.15	1	0.55	3.68	17.6	Sangster, 1994; Obach, 1999; Avdeef, 2003
Glyburide	A	0.0012 (16%)	0.72 (9%)	4.29	5.38	1	0.57	2.59	4.81	Austin et al., 2002; Li et al., 2017
Ketoprofen	A	0.0041 (9%)	0.95 (4%)	3.12	4.45	1	0.56	2.06	5.02	Sangster, 1993, 1994; Rodgers and Rowland, 2007; Ye et al., 2016
Nafcillin	A	0.123 (6%)	0.94 (14%)	2.7	2.6	1	0.55d	1.66	33.9	Wishart et al., 2018
Warfarin	A	0.0076 (13%)	0.98 (16%)	2.7	5.05	1	0.55	1.66	0.179	Hiskey et al., 1962; Hansch et al., 1995; Obach, 1999

A, acids; B, bases; N, neutral; CL, clearance; vo, vegetable oil.

^aAll 98 experimental values unless otherwise noted.

^bRat BP was used.

^cAn average of literature values was used.

^d0.55 was used (1-hematocrit).

The log P_vo (log of the vegetable oil:buffer partition coefficient) was calculated from log P using eq. 1 (Leo et al., 1971). This term is used to represent neutral lipid partitioning in adipose tissue in the K_p,dPL method; however, it is not used in the K_p,mem prediction method:

(1)

Microsomal Partitioning and Plasma Protein Binding.

Equilibrium dialysis was used to determine the f_up and f_um for the probe drugs using a protocol modified from prior studies (Kochansky et al., 2008; Curran et al., 2011; Di et al., 2017). Human plasma was adjusted to pH 7.4 by adding 1 M HCl. For f_um determination, a 0.5 mg/ml rat liver microsomal solution was prepared from a 20 mg/ml pooled rat liver microsome stock solution. For highly bound compounds, a dilution method was used. Plasma was diluted using a 100 mM phosphate buffer and 3 mM MgCl₂ solution to either 50% or 10% plasma. A 50% dilution of plasma was used for warfarin, while a 10% dilution was used for ketoprofen, nicardipine, glyburide, diclofenac, felodipine, and mibefradil. Drug solutions (2 μM) in either plasma or microsomes were added to wells on one side of the dialyzer, and blank 100 mM phosphate buffer with 3 mM of MgCl₂ was added to the other side. The dialyzer plate was placed in the plate rotator, set to a speed of approximately 22 rotations per minute, and incubated for 22 hours at 37°C and 5% CO₂. Liquid chromatography–tandem mass spectrometry was used to determine the concentration of drug in the buffer and the matrix.

The fraction unbound in a given matrix was determined by dividing the concentration of drug on the buffer side by the concentration of drug on the matrix side. For protein binding experiments using the dilution method, the f_up value is calculated by eq. 2:

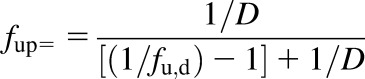(2)

where D is the dilution factor; f_u,d is the fraction unbound in plasma measured in the diluted matrix; and f_up is the fraction unbound in plasma.

Experimental f_um values were measured at microsomal concentrations between 0.5 and 2 mg/ml and converted to values for 1 mg/ml (eq. 3) (Austin et al., 2002):

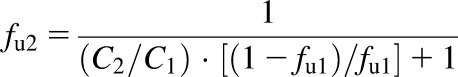(3)

where f_u2 is the corrected unbound fraction; C₂ is the 1 mg/ml microsomal protein concentration; C₁ is the microsomal protein concentration used in assay; and f_u1 is the fraction unbound in matrix measured during the assay. The average fraction unbound, S.D., and CV values were determined for each assay.

Simulations.

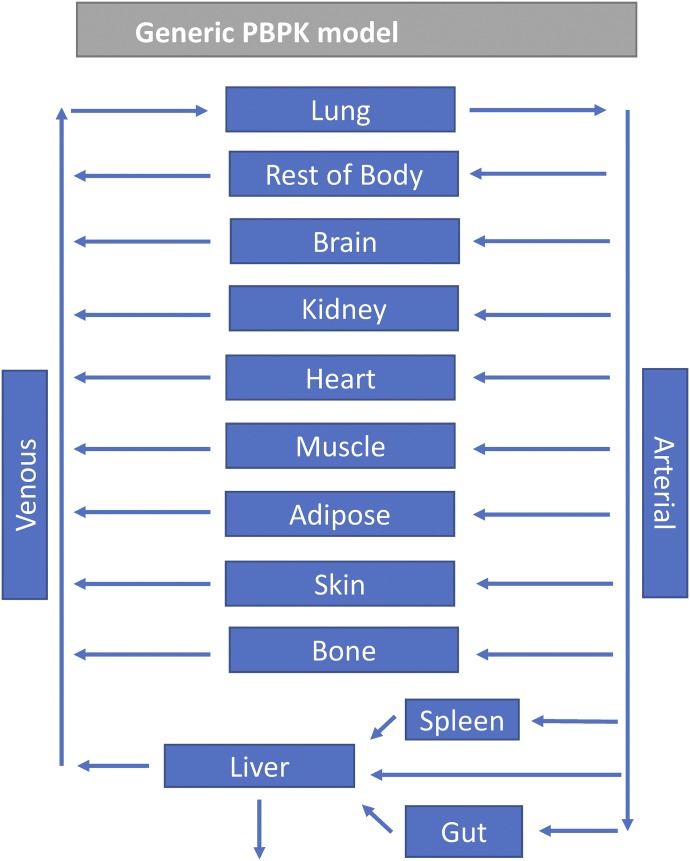
A generic PBPK model was used, with different tissues represented by 10 compartments (adipose, bone, brain, gut, kidney, liver, lungs, muscle, skin, and spleen), representing the major tissues in the body (Fig. 1). These compartments are linked via arterial and venous blood flows. The K_p values were predicted for each of the tissues using both methods (K_p,dPL and K_p,mem). The original K_p,dPL method uses two separate equations, one for acids, weak bases, and neutrals, and another for moderate-to-strong bases (eqs. 4–7) (Rodgers et al., 2005; Rodgers and Rowland, 2006).

Fig. 1.

Scheme for the generic PBPK model used in this study.

The K_p,dPL equation used for prediction of K_pu for strong-to-moderate bases is

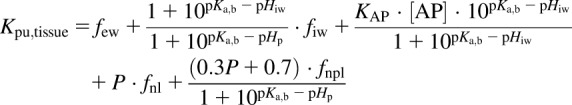(4)

where f_ew is the fractional volume of extracellular water; f_iw is the fractional volume of intracellular water; [AP] is the concentration of acidic phospholipids in the tissue; K_AP is the association constant for acidic phospholipids in the tissue; f_nl is the fractional volume of neutral lipids; f_npl is the fractional volume of neutral phospholipids; pK_a,b is the basic ionization constant; and pK_a,a is the acidic ionization constant.

The Rodgers equation used for prediction of K_pu for acids, neutrals, and weak bases is

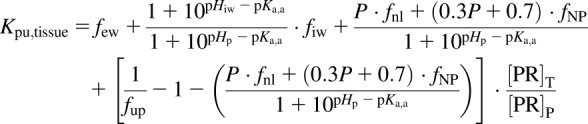(5)

where [PR]_T/[PR]_P is the plasma protein tissue (extracellular fluid) to plasma ratio, and NP denotes neutral phospholipid.

For eq. 4, the association constant for blood cells (BCs) is defined in eq. 6, and the tissue:plasma water partitioning coefficient for the BCs is defined in eq. 7:

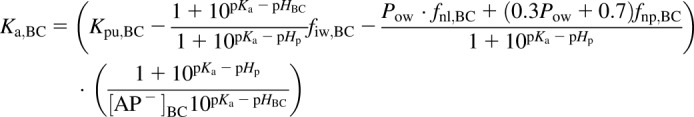(6)

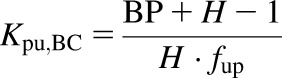(7)

The tissue:plasma partition coefficient (K_p) can be determined from K_pu by eq. 8:

(8)

For the K_p,mem method we use the previously reported equation (Korzekwa and Nagar, 2017a) that considers both phospholipid membrane partitioning with f_um and neutral lipid partitioning with P (eq. 9):

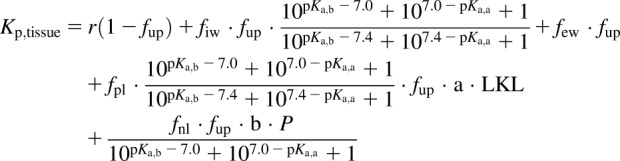(9)

where r is the protein ratio between the tissue and plasma; f_pl is the fractional volume of phospholipid; LKL is the lipid binding constant; and a and b are parameterized coefficients. Plasma and tissue pH values were assumed to be 7.4 and 7.0, respectively. As described previously for V_ss predictions (Korzekwa and Nagar, 2017a), the tissue-specific r values for bases were decreased by 2.23-fold due to the lower amount of α-acid glycoprotein in the extracellular fluid relative to albumin (Rowland and Tozer, 2011).

Neutral lipid partitioning in adipose tissue is described by the vegetable oil:water partition coefficient in the K_p,dPL method, which is generally calculated from log P. In the K_p,mem prediction method log P is used directly. The a and b terms in eq. 9 were parameterized using the tissue K_p values and tissue composition data from Rodgers et al. (2005) and Rodgers and Rowland (2006). We excluded zwitterions and combined neutral and acidic phospholipids to obtain a fraction of the total phospholipids. Most f_um values were calculated with our previously reported model (Nagar and Korzekwa, 2017) since experimental values are not available for this data set. The log K_pu values and the log of eq. 9 were used to fit a and b, with no additional weighting (log transformation results in 1/Y weighting). Outliers were identified using the BoxWhisker function (Frigge et al., 1989) in Mathematica with outliers defined as >1.5 times the interquartile range. Another model, which included an additional parameter for partitioning into adipose, was evaluated but did not improve predictions. The lipid concentrations multiplied by the lipid binding constant, L times K_L, (LKL), was calculated from f_um with eq. 10, using f_um values normalized to 1 mg/ml microsomal protein:

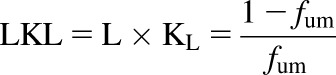(10)

Exposure overlap coefficients (EOCs) were used to quantify the ability to predict the shape of the C-t profile (eq. 11) (Nagar et al., 2017). They are calculated by determining the overlapping portion of the experimental and predicted C-t profile curves and dividing that area by the experimental area under the curve (AUC). Since the experimental clearance values were used for all predictions, both experimental and predicted C-t profiles will have the same AUC. This allows the EOC to be used as a direct comparison of curve shapes. Differences in the average EOCs were determined using the t test:

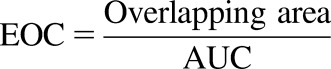(11)

V_ss Predictions.

The V_ss value was determined from the predicted K_p values and physiologic volumes (eq. 12):

(12)

where V_p is the plasma volume, and V_t represents the tissue volume.

Predicted V_ss values were compared with observed values determined by compartmental modeling. To evaluate the predictive precision of the two methods, the absolute fold-error and absolute average fold error (AAFE) values were determined for all compounds and different subsets. Significance of differences in absolute fold errors were determined with a one-tailed t test. The AAFE determines the geometric mean of the absolute fold error (eq. 13) and is a measure of how precisely the two methods predict V_ss:

(13)

where n is the number of drugs, and FE is the fold error.

Results

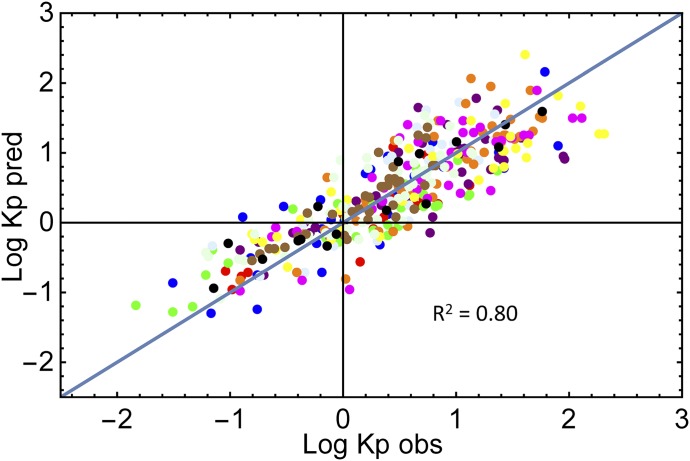
The parameters a and b in eq. 9 were fit to the experimental tissue reported K_pu values for the rat (Rodgers et al., 2005; Rodgers and Rowland, 2006). After sequential removal of 20 outliers (out of 401), the optimized parameters were a = 1383 ± 85 and b = 0.096 ± 0.029. The predicted versus observed K_pu values for 381 drugs are shown in Fig. 2. The R² value for the fit was 0.80. There was no consistent characteristic for the removed outliers with the exception of the overprediction of phencyclidine in four tissues and the underprediction of basic compounds in the lung (five drugs).

Fig. 2.

Observed vs. predicted rat K_pu values from eq. 10: blue, adipose; red, bone; green, brain; purple, gut; light blue, heart; orange, kidney; magenta, liver; yellow, lung; light green, muscle; brown, skin; black, spleen.

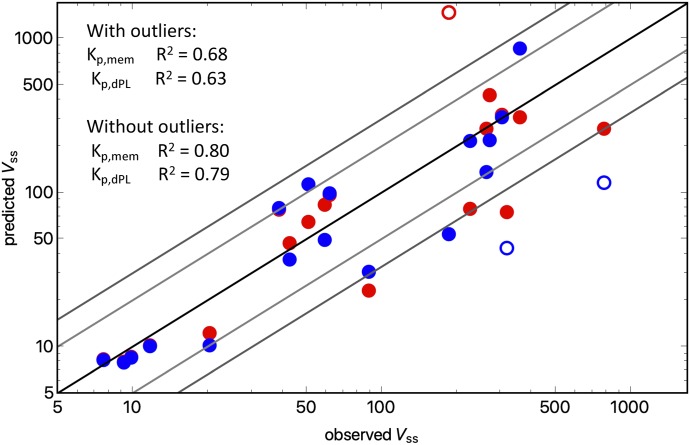
Figure 3 and Table 3 show the observed versus predicted V_ss values using either the K_p,dPL or K_p,mem prediction method. The accuracy of the V_ss predictions was analyzed by determining the percentage of predictions within a range of absolute fold errors (Table 4) and AAFEs (Table 5). For the total data set of 19 drugs, the K_p,mem and K_p,dPL methods had comparable AAFE values (2.12 and 2.27, respectively). The K_p,mem and K_p,dPL methods had one (mibefradil) and two (diphenhydramine, felodipine) outliers, respectively. When these were excluded, the AAFEs were again comparable.

Fig. 3.

Observed V_ss value vs. predicted V_ss value for 19 drugs: blue, K_p,dPL; red, K_p,mem.

TABLE 3.

Observed and predicted V_ss and EOC values for both methods

Test Drug	Observed Vss	Predicted Vss		EOC
		Kp,mem Method	Kp,dPL Method	Kp,mem Method	Kp,dPL Method
	l	l	l
Betaxolol	360	307	856	0.97	0.61
Diltiazem	306	320	309	0.76	0.80
Diphenhydramine	788	260	115	0.97	0.87
Metoprolol	274	429	217	0.76	0.87
Mibefradil	187	1470	53.2	0.81	0.82
Nicardipine	62	96.4	98.5	0.79	0.78
Quinidine	227	78.3	215	0.96	0.73
Verapamil	266	258	136	0.73	0.76
Caffeine	42.8	47.0	36.7	0.87	0.93
Diazepam	89.5	22.9	30.5	0.55	0.61
Felodipine	320	74.3	43.4	0.68	0.56
Fluconazole	59.3	83.4	49.1	0.85	0.99
Midazolam	51.2	64.1	113	0.82	0.71
Phenytoin	38.8	77.0	79.1	0.78	0.77
Diclofenac	9.23	7.98	7.89	0.84	0.84
Glyburide	11.78	10.2	10.0	0.86	0.87
Ketoprofen	9.9	8.54	8.47	0.89	0.89
Nafcillin	20.4	12.2	10.1	0.86	0.81
Warfarin	7.66	8.20	8.15	0.96	0.97
			Average	0.82 ± 0.11	0.80 ± 0.12

TABLE 4.

Fraction of drugs in which the predictions had less than 1.5-, 2-, and 3-fold error

Category	<1.5-Fold Error		<2-Fold Error		<3-Fold Error
	Kp,mem	Kp,dPL	Kp,mem	Kp,dPL	Kp,mem	Kp,dPL
All Compounds	10/19	9/19	14/19	11/19	15/19	16/19
Acids	4/5	4/5	5/5	4/5	5/5	5/5
Bases	3/8	3/8	5/8	5/8	6/8	6/8
Neutrals	3/6	2/6	4/6	2/6	4/6	5/6
Log P <3	5/9	5/9	8/9	5/9	8/9	9/9
Log P >3	5/10	4/10	6/10	6/10	7/10	7/10
fum < 0.8	6/11	4/11	8/11	6/11	8/11	9/11
fum > 0.8	4/8	5/8	6/8	5/8	7/8	7/8
fup < 0.1	6/10	4/10	7/10	6/10	7/10	8/10
fup > 0.1	4/9	5/9	7/9	8/9	8/9	8/9

TABLE 5.

Absolute average fold error for V_ss predictions using both the K_p,mem and K_p,dPL prediction methods

Category	AAFE		AAFE (Excluding Outliers)
	Kp,mem	Kp,dPL	Kp,mem	Kp,dPL
All Compounds	2.12	2.27	1.80	1.70
Acids	1.24	1.32	1.24	1.32
Bases	2.52	2.45	1.76	1.82
Neutrals	2.32	2.82	2.32	1.91
Log P <3	1.66	1.68	1.66	1.68
Log P >3	2.54	2.81	1.95	1.73
fum < 80%	2.36	2.41	1.81	1.92
fum > 80%	1.79	2.07	1.79	1.39
fup < 10%	2.45	2.42	1.84	1.86
fup > 10%	1.76	2.11	1.76	1.56

Ten different categories are compared in Tables 4 and 5. For predictions that were less than 1.5-fold error, K_p,mem scored higher in five categories, lower in two categories, and the same in three categories compared with K_p,dPL (Table 4); for predictions that were less than 3-fold error, K_p,mem scored lower in five categories and the same in five categories compared with K_p,dPL. When comparing all 19 drugs, the AAFEs with K_p,mem versus K_p,dPL were 2.12 versus 2.27, respectively (Table 5). Across the 10 categories, the AAFE was lower for K_p,mem than for K_p,dPL in eight categories. When outliers were excluded in each method, the AAFE was lower for K_p,mem than for K_p,dPL in five categories. For all categories listed in Table 5, there were no statistically significant differences in average fold error between K_p,mem and K_p,dPL.

Simulations.

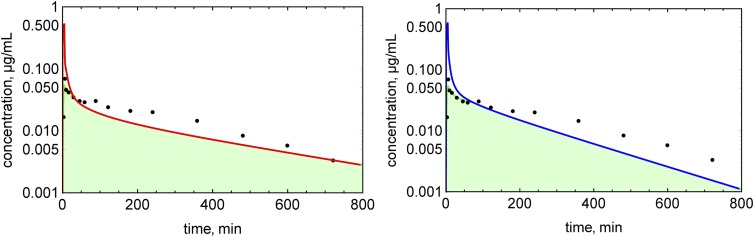
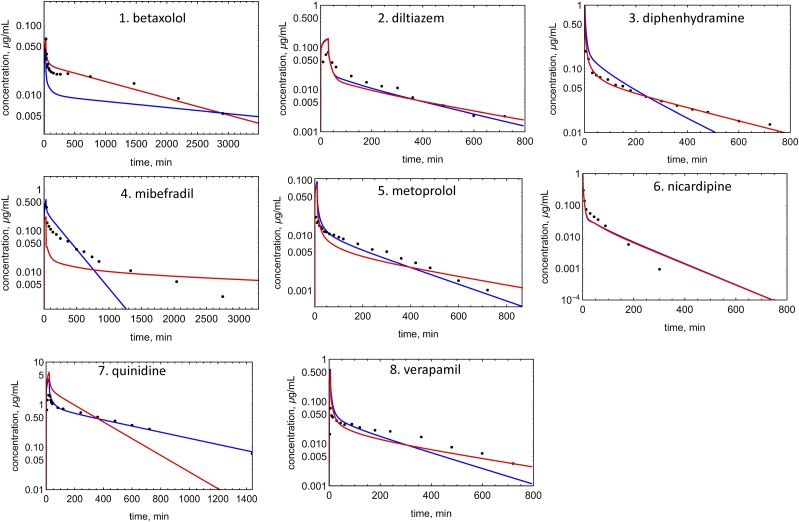
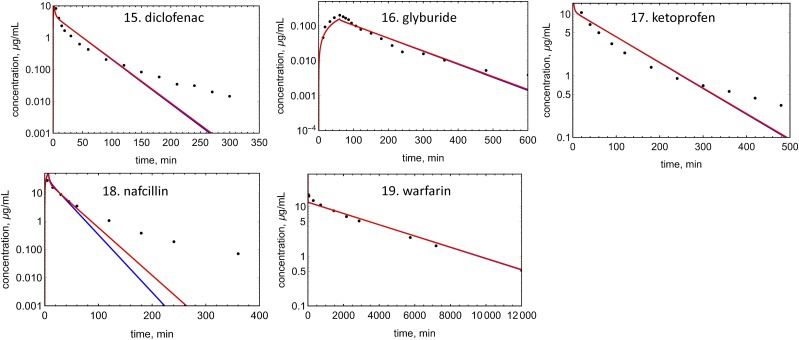
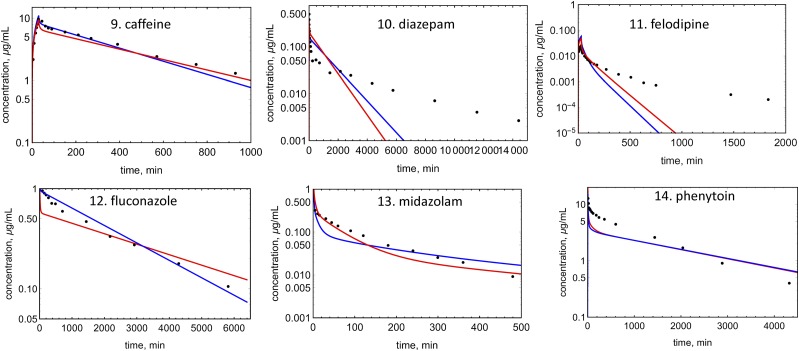
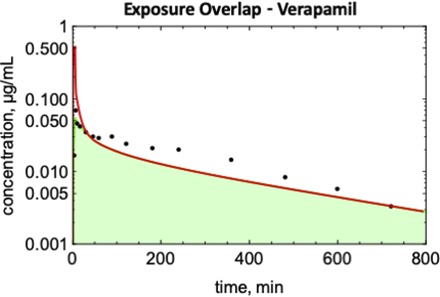
An example of EOC calculation is shown in Fig. 4 for verapamil. Concentration profiles were simulated for 19 drugs with both K_p prediction methods (Figs. 5–7). EOCs were determined for all 19 drugs (Table 3). Overall, there was no significant difference in the average EOC values for the K_p,mem or K_p,dPL method. However, there were some interesting deviations between the methods. The C-t profiles were poorly predicted by both methods for five drugs: mibefradil, diazepam, felodipine, diclofenac, and nafcillin. In addition, the K_p,dPL method poorly predicted the profiles for betaxolol and diphenhydramine. Some possible explanations for these discrepancies are discussed subsequently.

Fig. 4.

Determination of the exposure overlap coefficients for verapamil: red line, simulated C-t profile using the K_p,mem method; blue line, simulated C-t profile using the K_p,dPl method; green area, area of overlap.

Fig. 5.

Observed and predicted C-t profiles for bases: red lines, simulated C-t profile using the K_p,mem method; blue lines, simulated C-t profile using the K_p,dPl method; solid circles, experimental data.

Fig. 7.

Observed and predicted C-t profiles for acids: red lines, simulated C-t profile using the K_p,mem method; blue line, simulated C-t profile using the K_p,dPl method; solid circles, experimental data.

Fig. 6.

Observed and predicted C-t profiles for neutral molecules: red lines, simulated C-t profile using the K_p,mem method; blue lines, simulated C-t profile using the K_p,dPl method; solid circles, experimental data.

As discussed previously (Korzekwa and Nagar, 2017b), eqs. 5–7 indicate that the K_pu,tissue value, and ultimately the unbound V_ss value, should be proportional to K_pu,BC (eq. 7), which was first experimentally observed by Hinderling (1997). Also, f_up in the denominator of eq. 7 is ultimately multiplied by f_up in the PBPK framework (eq. 8). Therefore, the predicted V_ss values for bases should be relatively insensitive to f_up when using eqs. 4–7. The impact on the predicted V_ss after a 2-fold decrease in f_up is shown in Table 6. As expected, changing f_up for acids has little effect since plasma protein binding is high and V_ss is low. For neutrals, a 2-fold decrease in f_up results in an average 1.7-fold increase in V_ss for both methods. For bases, a 2-fold decrease in f_up results in an average 2-fold decrease in V_ss for K_p,mem, but an average 1.05-fold increase with K_p,dPL.

TABLE 6.

Impact of errors in f_up on V_ss

Compound	Fold Decrease in Vss upon a 2-Fold Decrease in fup
	Kp,mem	Kp,dPL
Betaxolol	1.97	0.95
Diltiazem	1.98	1.05
Diphenhydramine	1.94	0.82
Metoprolol	1.98	0.75
Mibefradil	2.00	0.95
Nicardipine	1.90	1.01
Quinidine	1.89 [average (bases)]	1.00 [average (bases)]
Verapamil	1.95 (1.95 ± 0.04)	1.06 (0.95 ± 0.11)
Caffeine	1.66	1.59
Diazepam	1.41	1.53
Felodipine	1.79	1.66
Fluconazole	1.82	1.70
Midazolam	1.78 [average (neutrals)]	1.86 [average (neutrals)]
Phenytoin	1.78 (1.71 ± 0.15)	1.79 (1.69 ± 0.12)
Diclofenac	1.01	1.01
Glyburide	1.05	1.03
Ketoprofen	1.01	1.00
Nafcillin	1.19 [average (acids)]	1.09 [average (acids)]
Warfarin	1.01 (1.05 ± 0.08)	1.01 (1.03 ± 0.04)

Discussion

Tissue partition coefficients, and ultimately V_ss, are determined primarily by competition between plasma protein binding and lipid partitioning. The K_p,dPL method considers binding to neutral lipids such as triglycerides and neutral phospholipids in membranes, with acidic phospholipids considered separately (Rodgers et al., 2005; Rodgers and Rowland, 2006). The method assumes that neutral molecules only interact with neutral phospholipids, and only ionized bases interact with APs, an assumption questioned previously (Korzekwa and Nagar, 2017b). The major acidic phospholipid is phosphatidylserine and the major neutral phospholipid is phosphatidylcholine. Although phosphatidylcholine is net neutral and phosphatidylserine is net acidic, both molecules are zwitterions. Interactions between charged species in the polar head group region are dynamic processes with conformational changes occurring in a picosecond time frame (Tieleman et al., 1997). Balaz (2009) compiled experimental data evaluating the orientation of exogenous molecules in membranes. Hydrophilic molecules accumulate in the polar head group region, amphiphilic molecules accumulate at the interface, and hydrophobic molecules accumulate in the hydrophobic core. We have used this concept to develop quantitative models for membrane partitioning (Nagar and Korzekwa, 2017).

The K_p,mem model is based on previously reported V_ss models (Korzekwa and Nagar, 2017a). The K_p model described herein uses the phospholipid component of tissues and f_um to model membrane partitioning and log P for neutral lipid interactions. Equation 9 was parameterized using reported tissue composition data and tissue K_p values (Rodgers et al., 2005; Rodgers and Rowland, 2006). Only two constants were parameterized: the scaling factor for 1) membranes and 2) neutral lipids. Although the two methods use different mechanistic assumptions, the resulting fit for K_p,mem (Fig. 2) is similar to that reported by Rodgers et al. (2005) for K_pu parameterization.

The volume of distribution is generally low for acids due to high plasma protein binding and low partitioning into membranes and neutral lipids. At physiologic pH, most acids are negatively charged, and membranes have few hydrogen bond donors. Therefore, microsomal partitioning is low for acids, with f_um values ranging from 0.72 to 0.98 (Table 2). Both the K_p,mem and K_p,dPL methods assume that only the neutral acids partitions into tissues, and both methods predict V_ss with similar accuracy (AAFE = 2.12 and 2.27 for K_p,mem and K_p,dPL, respectively) (Table 5). This is expected since any model that restricts a compound with low f_up to the plasma and extracellular space will predict a V_ss value approximately equal to that of plasma proteins (∼7.5 l) (Rowland and Tozer, 2011). Underprediction of acids with V_ss values >9, e.g., nafcillin, is frequently observed (Chan et al., 2018). Transporter activity (e.g., organic anion transporting polypeptides) could be one reason for the underprediction.

When two outliers for the K_p,dPL analysis (diphenhydramine and felodipine) are excluded, V_ss predictions for neutrals using K_p,dPL improved from an AAFE value of 2.82 to 1.91 (Table 5). For diphenhydramine, the K_p,dPL method resulted in a 6.9-fold underprediction and K_p,mem gave a 3-fold underprediction (not an outlier). For felodipine, K_p,dPL resulted in a 7.4-fold underprediction and K_p,mem gave a 4.3-fold underprediction (not an outlier). The reason for these poor predictions is unknown but it may be difficult to predict V_ss of a highly protein bound and partitioned neutral compound (felodipine).

The K_p,mem method uses a single equation for bases, neutrals, and acids and predicts V_ss for bases with similar accuracy to K_p,dPL, which uses different equations for bases (eqs. 5–7). The K_p,dPL method assumes that ionized bases only interact with acidic phospholipids. This interaction is parameterized with BP, using the erythrocyte partition coefficient to parameterize binding of the ionized base to acidic phospholipids. Mechanistically, the assumption that bases bind only to acidic phospholipids is questionable. Hydrophobic bases bind to neutral phospholipids as well, with key interactions between the cation and negatively charged phosphate, and the hydrophobic region with the hydrophobic membrane core. From eqs. 5–7, it is clear that for moderate-to-strong bases with V_ss values greater than the total body water, the K_p values are dominated by the acidic phospholipid binding terms. Therefore, although binding to only acidic phospholipids was assumed, a similar relationship is possible, assuming that ionized bases bind to all phospholipids. The ratio of neutral to acidic phospholipids is relatively constant across tissues (CV = 15%) (Rodgers et al., 2005), and total phospholipids can be substituted for neutral phospholipids. The K_BC term in eq. 6 would be smaller, but the relevant phospholipid term in eq. 5 would be larger.

Another implication of using BP to predict K_pu for bases is the insensitivity of V_ss to measured f_up. For acids, V_ss is insensitive to f_up since tissue partitioning is minimal. The V_ss values for bases are expected to be proportional to f_up since they partition heavily into tissues from the unbound concentration in cytosol (assumed to be equal to the unbound concentration in plasma). This is observed for K_p,mem but not for K_p,dPL (Table 6). This is a consequence of using BP (which includes f_up) to calculate K_pu. The V_ss predictions can be relatively accurate when BP is used to predict K_p for bases, since errors in f_up are not manifest and unbound V_ss for bases is proportional to erythrocyte partitioning (Hinderling, 1997). However, errors in f_up can still result in many other inaccuracies, including in predictions of clearance and target activity.

Overall, the K_p,mem and K_p,dPL models give similarly accurate predictions, explaining 68% and 63% of the variance in V_ss (80% and 79% without outliers), respectively. Several factors may explain the remaining variance. First, there can be significant variability in the V_ss values measured across clinical studies. Not all pharmacokinetic data sets provide body weights. Also, experimental data from multiple sources are used, e.g., BP values; for example, Graham et al. (2012) observed a 7% decrease in accuracy when predicted instead of experimental log P values were used. For f_up, differences between laboratories can be very large. Several recent publications discuss assay conditions for protein binding, including dilution and use of CO₂ (Kochansky et al., 2008; Curran et al., 2011; Di et al., 2017). In this study, we measured a value of f_up of 0.03 for mibefradil, whereas a value of <0.005 was reported previously (Clozel et al., 1991). Use of a smaller f_up value would result in a better prediction with K_p,mem, but exclusion of our data is not justified.

Lysosomal partitioning affects tissue distribution for bases. For strong bases, partitioning into lysosomes due to pH differences results in lysosomal concentrations >200 times cytosolic concentrations. Assuming 5% lysosomes and 60% intracellular water in cells, partitioning of a strong base into lysosomes can increase the K_pu value by 6-fold. As discussed previously, while lysosomal partitioning certainly occurs it is likely to be highly correlated with phospholipid partitioning of bases (Korzekwa and Nagar, 2017a). Finally, although the vegetable oil:water partition constant would be a good surrogate for adiposomes if measured, this value is typically modeled using log P, which is not necessarily accurate (Korzekwa and Nagar, 2017b).

Transporter-mediated distribution can result in inaccurate predictions of K_p and V_ss, particularly for some acids. Organic anion transporting polypeptide transporters can alter hepatic intracellular concentrations by two orders of magnitude (Kulkarni et al., 2016). Therefore, uptake into this organ alone can result in a 2-fold increase in V_ss. Efflux transporters (e.g., P-glycoprotein and breast cancer resistance protein) will have a smaller impact. The decrease in V_ss due to P-glycoprotein and breast cancer resistance protein at the blood-brain barrier would result in a 2% decrease in V_ss. The impact from the liver would be even smaller since efflux transporters in the apical membrane would only decrease liver concentrations by 50% (Korzekwa and Nagar, 2014).

Since the AUC is determined by experimental clearance and dose in both methods, the AUC values for the simulations are normalized, and the EOC captures differences in the shapes of the C-t profile (Fig. 4). Several C-t profiles in Figs. 5–7 are not well predicted by either method. Although there are differences in the EOC for some drugs, the average EOCs for the K_p,mem and K_p,dPL prediction methods were not significantly different. Since clearance is constant, when the V_ss value is overpredicted (e.g., betaxolol using K_p,dPL and mibefradil using K_p,mem) (Fig. 5), the terminal half-life is overpredicted. When the V_ss value is underpredicted (e.g., diphenhydramine using K_p,dPL) (Fig. 5), the terminal half-life is underpredicted. Perhaps the most significant deficiency of the reported modeling approaches is the assumption of perfusion-limited distribution. As seen with diazepam, felodipine, diclofenac, and nafcillin, accurate C-t profiles are not predicted even when the V_ss value is well predicted. For verapamil (Figs. 4 and 5), the distribution phase is not well predicted, presumably due to a combination of using a perfusion-limited model and experimental clearance. Clearly, multicompartmental distribution is not accurately modeled with perfusion-limited distribution.

In conclusion, K_p,mem can be used to predict K_pu with accuracy similar to K_p,dPL. An advantage of using f_um to parameterize membrane partitioning is that f_um is used for clearance prediction and is generated early in the discovery/development process. Also, differentiating between acidic and neutral phospholipids for bases and using 0.3P for neutral compounds is not mechanistically justified. Finally, since both the extent and rate of membrane partitioning and permeability are important, a mechanistically sound basis for membrane interactions is necessary for improved PBPK models.

Abbreviations

AAFE

absolute average fold error

AP

acidic phospholipid

AUC

area under the curve

BC

blood cell

BP

blood to plasma

C-t

concentration-time

EOC

exposure overlap coefficient

f_ew

fractional volume of extracellular water

f_iw

fractional volume of intracellular water

f_nl

fractional volume of neutral lipids

f_um

fraction unbound in microsomes

f_up

fraction unbound in plasma

K_p

tissue:plasma partition coefficient

K_p,dPL

differential phospholipid tissue-plasma partition coefficient prediction method

K_p,mem

membrane-based tissue-plasma partition coefficient prediction method

K_pu

unbound tissue:plasma partition coefficient

P

octanol:water partition coefficient

PBPK

physiologically based pharmacokinetic

pK_a,a

ionization constant for acids

pK_a,b

ionization constant for bases

V_ss

steady-state volume of distribution

Authorship Contributions

Participated in research design: Holt, Nagar, Korzekwa.

Conducted experiments: Holt, Ye.

Performed data analysis: Holt, Nagar, Korzekwa.

Wrote or contributed to the writing of the manuscript: Holt, Nagar, Korzekwa.