Figure 9.

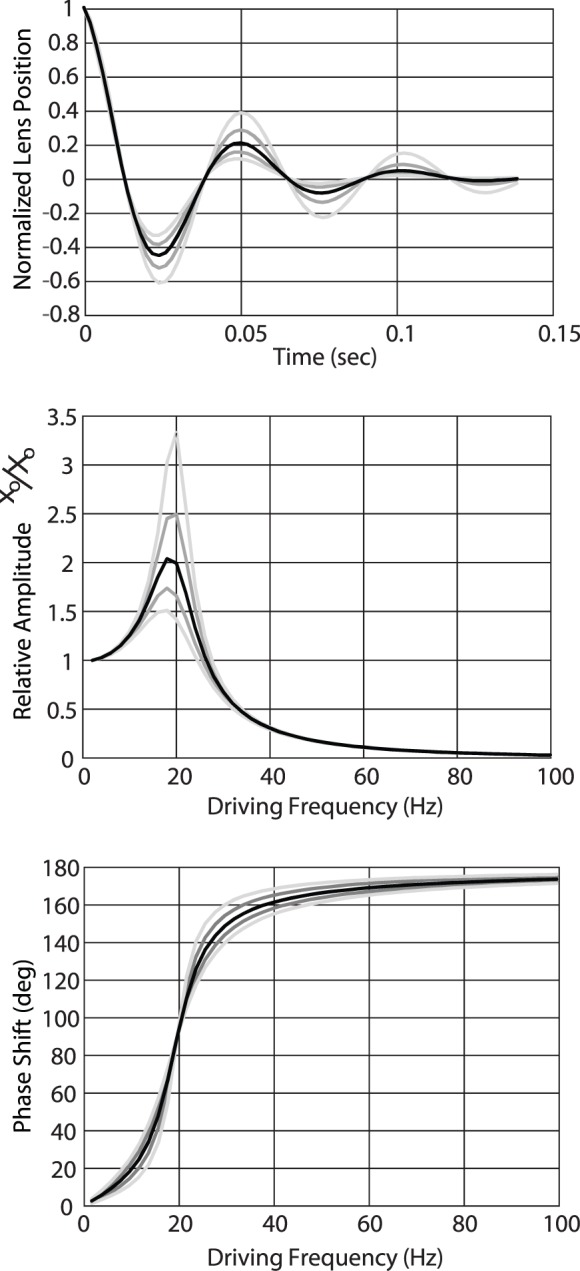
(A) Model of the position of a lens behaving as damped harmonic oscillator. In this case, the damping coefficient is 20π (10 Hz), or half of the resonant frequency of 20 Hz, which leads to about two cycles of oscillation before relaxing to zero. Gray shaded lines in all three plots show calculations with ±20% and ±40% changes in the damping coefficient. (B) Model of the amplitude of a lens behaving as a driven damped harmonic oscillator with resonant frequency of 20 Hz and range of damping coefficients. Driving frequencies near the resonant frequency gives rise to amplified motion of the lens. Driving frequencies within the range of tremor give rise to lens oscillations that are, on average, about 0.1 of the driving amplitude. Amplitudes of lens motion at the resonant frequency are highly dependent on the damping coefficient, but outside of that the trends are relatively similar. (C) Model of the phase shift of the lens motion. When driving frequencies are slow, the lens moves along with the eyeball as expected. For driving frequencies that are in the range of tremor (50–100 Hz) the lens moves in counter-phase with the eyeball. Changes in the damping coefficient have little effect on this trend.