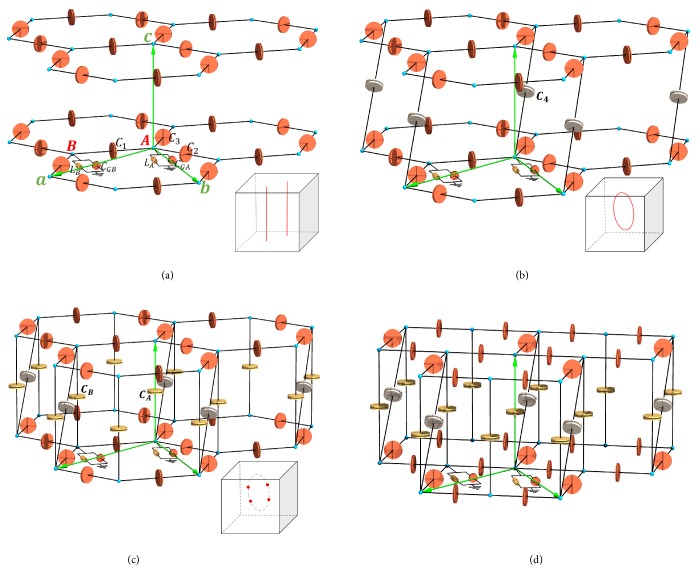
Figure 1.

Schematic setup of the three-dimensional LC circuit lattice. (a) Honeycomb layers consisting of inductors and capacitors stack along c direction without connection between each layer. The primitive unit cell consists of two inequivalent nodes A and B, which are linked by capacitors C₁, C₂, and C₃ in the a-b plane. Each node A (B) is grounded through the parallel connected inductor L_A (L_B) and capacitor C_GA (C_GB). Lattice vectors are denoted as a, b, and c. The frequency bands structure of the single layer honeycomb LC lattice has two band-crossing points, which are uniform in k_c direction and form two straight nodal lines in the BZ (red colour lines in the inset). (b) Connecting nodes A and nodes B between neighbor-layers with C₄. The nodal lines become k_c dependent and form a closed ring by choosing appropriate C₄. (c) Connecting nodes A-A and nodes B-B between neighbor-layers with C_A and C_B, respectively, and removing the space inversion symmetry by tuning C_A ≠ C_B and C_GA ≠ C_GB, the nodal ring may be degenerated to Weyl points. The LC lattice can be deformed into (d), which brings convenience for constructing circuit elements in experiments with spectrum topologically invariable.