Control and Plasticity of Intercellular Calcium Waves in Astrocytes: A Modeling Approach

Abstract

Intercellular Ca²⁺ waves in astrocytes are thought to serve as a pathway of long-range signaling. The waves can propagate by the diffusion of molecules through gap junctions and across the extracellular space. In rat striatal astrocytes, the gap-junctional route was shown to be dominant. To analyze the interplay of the processes involved in wave propagation, a mathematical model of this system has been developed. The kinetic description of Ca²⁺ signaling within a single cell accounts for inositol 1,4,5-trisphosphate (IP₃) generation, including its activation by cytoplasmic Ca²⁺, IP₃-induced Ca²⁺ liberation from intracellular stores and various other Ca²⁺transports, and cytoplasmic diffusion of IP₃ and Ca²⁺. When cells are coupled by gap junction channels in a two-dimensional array, IP₃ generation in one cell triggers Ca²⁺ waves propagating across some tens of cells. The spatial range of wave propagation is limited, yet depends sensitively on the Ca²⁺-mediated regeneration of the IP₃ signal. Accordingly, the term “limited regenerative signaling” is proposed. The gap-junctional permeability for IP₃ is the crucial permissive factor for wave propagation, and heterogeneity of gap-junctional coupling yields preferential pathways of wave propagation. Processes involved in both signal initiation (activation of IP₃ production caused by receptor agonist) and regeneration (activation of IP₃production by Ca²⁺, loading of the Ca²⁺ stores) are found to exert the main control on the wave range. The refractory period of signaling strongly depends on the refilling kinetics of the Ca²⁺ stores. Thus the model identifies multiple steps that may be involved in the regulation of this intercellular signaling pathway.

Ca²⁺signals provide a mechanism for the integration and transmission of information. In astrocytes, the most abundant glial cell type in the CNS, Ca²⁺ signals are observed in response to neurotransmitters (Verkhratsky et al., 1998). These can travel as intercellular Ca²⁺ waves (ICWs) over several hundred micrometers and may thus provide a basis for a long-range signaling pathway (Cornell-Bell et al., 1990). ICWs have been described in a great number of primary astrocyte cultures (Charles and Giaume, 2002), in organotypic cultures (Dani et al., 1992;Harris-White et al., 1998), and in intact retina (Newman and Zahs, 1997), as well as in many other tissues, including epithelial cells (Sanderson, 1995) and the liver (Robb-Gaspers and Thomas, 1995;Dupont et al., 2000b). Recently, Ca²⁺ increases have been observed to trigger the release of glutamate from astrocytes and thereby modulate synaptic transmission (Araque et al., 1999).

A mechanism for ICWs was deduced from experiments performed on airway epithelial cells (Sanderson et al., 1990) and formulated as a mathematical model (Sneyd et al., 1994, 1995). It is based on the diffusion of inositol 1,4,5-trisphosphate (IP₃) from a stimulated cell through gap junction channels into neighboring cells where it elicits Ca²⁺ release from internal stores. Accordingly, ICW properties are determined by the production of IP₃ in a single cell and its diffusion and degradation in downstream cells. By contrast, in the long-ranging periodic Ca²⁺ waves in the liver, a messenger diffusing through gap junction channels appears to be regenerated in each participating cell (Robb-Gaspers and Thomas, 1995), and mathematical models addressing the underlying mechanisms are being developed (Höfer, 1999; Dupont et al., 2000a).

In the present paper, a mathematical model is proposed for astrocytic ICWs and compared with the experimental data. In astrocytes, the propagation process is complex, because besides gap junction-mediated intercellular diffusion (Giaume and Venance, 1998), the release of ATP into the extracellular space provides an additional route contributing to ICWs (Hassinger et al., 1996; Cotrina et al., 1998; Guthrie et al., 1999). Either the gap-junctional or the extracellular pathway, or both, can be present, depending on the origin of the astrocytes and the trigger for ICWs (Scemes et al., 2000; Charles and Giaume, 2002). The present study is based on previous experimental work performed with astrocytes cultured from rat striatum, in which ICWs predominantly propagate through gap junctions (Venance et al., 1995, 1997, 1998;Giaume and Venance, 1998). A further important finding was the existence of a regenerative step in the propagation mechanism: IP₃ is not only produced in the cell directly stimulated with agonist, but can also be generated in downstream cells, probably through the activation of phospholipase C (PLC) by Ca²⁺. The theoretical analysis presented shows that the proposed mechanism including IP₃diffusion and regeneration is indeed compatible with the limited spatial range of ICWs seen in the experiments and can account for many of the observed features of wave propagation. The model is then used to elucidate several critical steps that control the properties of this long-range signaling pathway.

MATHEMATICAL MODEL

The calcium and IP₃ dynamics are modeled by describing the Ca²⁺ transport processes and IP₃ production and degradation in a single astrocyte. The interior of each cell is spatially resolved, such that the intracellular diffusion of Ca²⁺ and IP₃ is also accounted for. A two-dimensional network of cells is considered, reflecting the monolayer arrangement of an astrocyte culture. Neighboring cells in the network are coupled by gap junction channels.

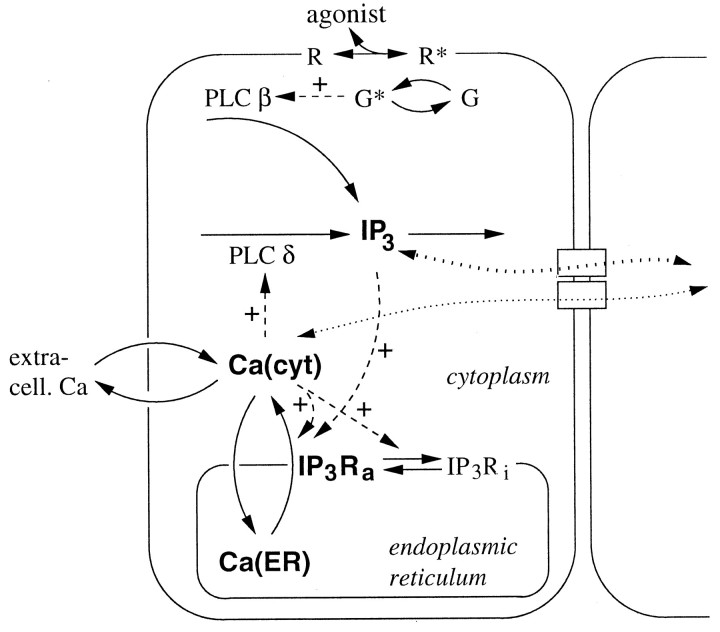
Based on the detailed pharmacological characterization of ICW propagation in rat striatal astrocytes by Venance et al. (1997), the scheme of Figure 1 is proposed for the intracellular dynamics. It includes the main Ca²⁺ transport processes known to be present in astrocytes: Ca²⁺ release from and uptake into IP₃-sensitive stores of the endoplasmic reticulum (ER) and Ca²⁺extrusion and entry across the plasma membrane. External agonists acting on G-protein-coupled receptors stimulate PLCβ. The resulting rise in IP₃ initiates Ca²⁺ discharge from the ER through IP₃ receptor channels (IP₃Rs). In the experiments, agonist was applied locally to a single cell, which will be termed “stimulated cell.” Others cells in the field, referred to as “downstream cells,” do not receive the agonist stimulus.

Fig. 1.

Scheme of the Ca²⁺ and IP₃ dynamics included in the model. Solid,dashed, and dotted arrows indicate reaction/transport steps, regulatory interactions, and molecular diffusion, respectively. The bold quantities indicate the model variables. R, Agonist receptor; G, G-protein (active forms are denoted by asterisks);IP₃R_i, inactive conformation of the IP₃ receptor. For further abbreviations and explanation see Mathematical Model.

Ca²⁺ elevation in astrocytes stimulates the production of IP₃ (Venance et al., 1997). This correlates with the finding that the PLCδ isoform is preferentially expressed in astrocytes within the CNS (Rebecchi and Pentyala, 2000). PLCδ is activated by Ca²⁺ signals in the physiological concentration range, and it may thus provide a molecular basis for the regeneration of IP₃ in nonstimulated cells. In the model we therefore include two distinct production terms for IP₃, one corresponding to PLCβ, which is activated through G-protein-coupled receptors exclusively in the stimulated cell, and the other to PLCδ, activated by Ca²⁺ elevation in the stimulated cell and in downstream cells.

The reaction scheme of Figure 1 is translated into a system of balance equations for the four variables: cytoplasmic Ca²⁺ concentration (C), ER store Ca²⁺ concentration (S), IP₃ concentration (I), and active fraction of IP₃R (R). It reads:

$$\partial C/\partial t=v_{\text{rel}}-v_{SERCA}+v_{\text{in}}-v_{\text{out}}+D_{\text{Ca}}({\partial }^{2}C/\partial x^2+{\partial }^{2}C/\partial y^2),$$ Equation 1

$$\partial S/\partial t=\beta (v_{SERCA}-v_{\text{rel}}),$$ Equation 2

$$\partial R/\partial t=v_{\text{rec}}-v_{\text{inact}},$$ Equation 3

$$\partial I/\partial t=v_{PLC\beta }+v_{PLC\delta }-v_{\text{deg}}+D_{IP3}({\partial }^{2}I/\partial x^2+{\partial }^{2}I/\partial y^2),$$ Equation 4

where v_PLCβ,v_PLCδ, v_deg,v_rel,v_SERCA,v_in, andv_out denote the rates of PLCβ, PLCδ, IP₃ degradation, Ca²⁺ release from the ER, Ca²⁺ pumping into the ER, Ca²⁺ influx across the plasma membrane, and Ca²⁺ extrusion. The last terms in the equations for cytoplasmic Ca²⁺ and IP₃ give the concentration changes caused by cytoplasmic diffusion, with the diffusion coefficientsD_Ca andD_IP3, respectively. In addition to the activation of the IP₃R by cytoplasmic Ca²⁺, we also account for a slower Ca²⁺-induced inactivation (Bezprozvanny et al., 1991; Tang et al., 1996), reflected by Equation 3. The rates of receptor inactivation and recovery are denoted by v_inact andv_rec, respectively. In Equations 1 and2, the effects of (fast) Ca²⁺ buffering in the cytoplasm and in the ER stores are accounted for by defining effective rate constants and an effective diffusion coefficientD_Ca (Wagner and Keizer, 1994;Höfer et al., 2001).

The cells are coupled through gap junction channels to their nearest neighbors (Finkbeiner, 1992; Venance et al., 1997). In primary cultures of astrocytes used for the Ca²⁺ imaging experiments, counting the cells surrounding a stimulated cell in concentric rows yielded 7 ± 1 (n = 7), 15.5 ± 2.5 (n = 11), and 22 ± 3 (n = 6) cells for the first, second, and third rows, respectively. Thus a regular array of square cells (with 8 × N cells in theN-th row) is used as a reasonable approximation in the model simulations. Cells are coupled by diffusive gap-junctional fluxes of IP₃ and Ca²⁺. Denote the spatial coordinates by x and y, and consider a cell–cell contact located at x = ξ. Assuming Fick's law, the intercellular flux conditions read:

$$-D_{\text{Ca}}\partial C/\partial x{\Vert }_{\text{x}=\xi }=P_{\text{Ca}}[C({\xi }^{-},y,t)-C({\xi }^{+},y,t)],$$ Equation 5a

$$-D_{IP3}\partial I/\partial x{\Vert }_{\text{x}=\xi }=P_{IP3}[I({\xi }^{-},y,t)-I({\xi }^{+},y,t)],$$ Equation 5b

where (ξ⁻, y) and (ξ⁺, y) denote the spatial positions immediately at the gap junctions in the left and right cells, respectively. Analogous conditions hold for cell–cell boundaries along the y-direction. The parametersP_Ca andP_IP3 are the gap-junctional permeabilities for Ca²⁺ and IP₃. They may differ because of intrinsic properties of gap junction channels (e.g., charge and size selectivity) and because of the effect of fast Ca²⁺buffering included in P_Ca(Höfer, 2001). In particular, in the following we assume that, because of calcium buffering, P_Ca ≪P_IP3.

The rate laws are chosen as follows. IP₃-induced and Ca²⁺-induced Ca²⁺ release is modeled according to the empirical fit in Bezprozvanny et al. (1991) as:

$$v_{\text{rel}}=[k_1+k_{2}R C^2{I}^2/(K_{\text{a}}^2+C^2)/(K_{IP3}^2+I^2)](S-C),$$ Equation 6

where the meanings of the various parameters in this and the following rate expressions are given in Table1. The release is a function of the IP₃R fraction in the active state R; the rates of receptor inactivation by Ca²⁺binding and recovery are taken as:

$$v_{\text{rec}}-v_{\text{inact}}=k_6[K_{\text{i}}^2/(K_{\text{i}}^2+C^2)-R],$$ Equation 7

(cf. Bezprozvanny et al., 1991; Atri et al., 1993).

Table 1.

Model parameters

Parameter	Symbol	Value
Rate constant of calcium leak from ER	k1	0.0004 sec−1
Rate constant of calcium release through IP3R	k2	0.08 sec−1
Rate constant of SERCA pump	k3	0.5 sec−1
Rate of calcium leak across the plasma membrane	v40	0.025 μm/sec−1
Maximal rate of activation-dependent calcium influx	v41	0.2 μm/sec−1
Rate constant of calcium extrusion	k5	0.5 sec−1
Rate constant of IP3R inactivation	k6	4 sec−1
Maximal rate of PLCδ	v7	0–0.05 μm/sec−1
Rate of PLCβ	v8	4 × 10−4 − 3 μm/sec−1
Rate constant of IP3 degradation	k9	0.08 sec−1
Half-saturation constant for IP3activation of IP3R	KIP3	0.3 μm
Half-saturation constant for calcium activation of IP3R	Ka	0.2 μm
Half-saturation constant for calcium inhibition of IP3R	Ki	0.2 μm
Half-saturation constant for calcium activation of PLCδ	KCa	0.3 μm
Half-saturation constant for agonist-dependent calcium entry	Kr	1 μm
Diffusion coefficient of IP3	DIP3	280 μm sec−2
Effective diffusion coefficient of calcium	DCa	20 μm sec−2
Gap-junctional permeability of IP3	PIP3	1–5 μm sec−1
Effective gap-junctional permeability of calcium	PCa	0.01PIP3
Ratio of the effective volumes for Ca2+ of cytoplasm and ER	β	20

The second component of the positive feedback between Ca²⁺ and IP₃, PLCδ activity, is modeled by:

$$v_{PLC\delta }=v_7{C}^2/(K_{\text{Ca}}^2+C^2),$$ Equation 8

giving a close fit to the data of Pawelczyk and Matecki (1997). The rate of PLCβ is controlled by the agonist; in the model we assign it a constant value for a fixed period of time. Assuming a simple collision scheme for the activation of PLCβ by G-protein, one obtains for its activity at saturating ligand concentrations:

$$v_{PLC\beta }=v_8[(1+{\kappa }_G)({\kappa }_G/(1+{\kappa }_G)+{\alpha }_0){]}^{-1}{\alpha }_0,$$ Equation 9

where κ_G and α₀denote, respectively, the ratio of the dissociation constant for G-protein binding to PLCβ to the total concentration of G-protein, and the ratio of the total concentration of agonist receptors to the dissociation constant for receptor binding to the G-protein. Ca²⁺ pumping and IP₃degradation are modeled by linear rate laws:

$$v_{SERCA}=k_3 C,v_{\text{out}}=k_5 C,v_{\text{deg}}=k_9 I.$$ Equation 10

The Ca²⁺ entry rate expression accounts for a small leak flux that is always present and an agonist-dependent influx (which can be receptor-operated or store-operated Ca²⁺ influx, or both). For simplicity, the latter is made a function of IP₃ concentration as a measure of agonist dose (cf. Dupont and Goldbeter, 1993):

$$v_{\text{in}}=v_{40}+v_{41}{I}^2/(K_{\text{r}}^2+I^2).$$ Equation 11

The rate constants for the Ca²⁺dynamics (k₁ throughk₅,v₄₀,v₄₁) and of PLCβ were estimated by fitting the model to resting values of cytosolic and stored Ca²⁺, and to agonist-evoked Ca²⁺ spikes and the store emptying kinetics measured by Venance et al. (1997) (T. Höfer, unpublished results). Other parameters (k₉,D_Ca,D_IP3,K_a,K_IP3,K_i,K_Ca) were taken from the experimental literature. No direct measurements exist in astrocytes for the maximal rate of PLCδ and the permeabilities of gap junction channelsP_IP3 andP_Ca, yet these parameters are expected to be crucial for the model behavior. Therefore, the model solutions are analyzed under systematic variation of these parameters. Estimates of gap-junctional permeability ranges are available for other cell types and permeating substances (Verselis et al., 1986; Eckert et al., 1999) and are used as guidance. The values of the model parameters are listed in Table 1.

Model solutions were obtained numerically by discretizing the system of Equations 1-4 on a regular square grid, using explicit Euler stepping for the kinetics combined with an alternating direction implicit (ADI) scheme for the diffusion terms (Morton and Mayers, 1993). The intercellular flux conditions (Eqs. 5a, 5b) are discretized by a scheme used previously (Sneyd et al., 1995; Höfer et al., 2001). To adjust numerical parameters, one-dimensional solutions were obtained with an implicit finite-difference scheme and compared with solutions computed with a method of lines/adaptive-stepsize Runge–Kutta scheme. Space and time steps chosen for the ADI scheme were 5 μm and 50 msec, respectively.

RESULTS

Single-cell responses to stimulation with receptor agonists of different potency

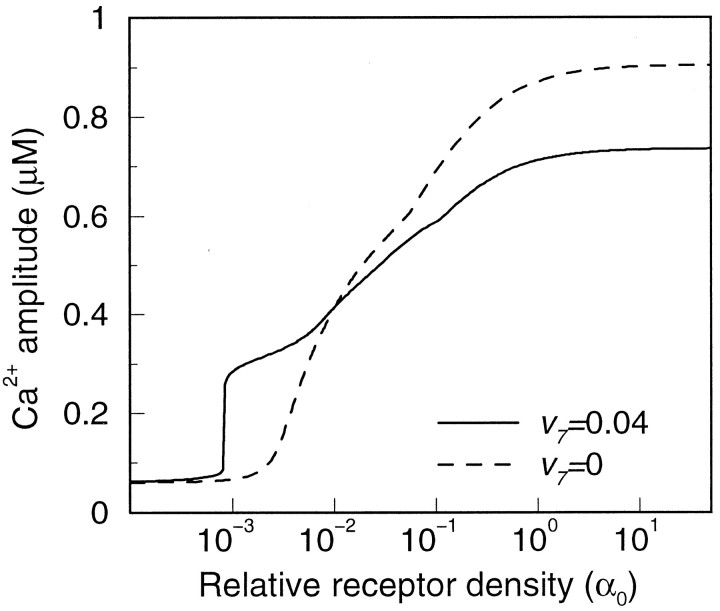
The experimental data show that saturating doses of different agonists evoke responses of different magnitude. The Ca²⁺ amplitudes increased in the following order: carbachol/methoxamine < glutamate (Glu) < endothelin-1 (ET-1) (Venance et al., 1997). A molecular basis for this behavior is indicated by the observation that α1-adrenergic (for methoxamine) and muscarinic (for carbachol) receptors are expressed at much lower overall densities (and are distributed more heterogeneously) than glutamate and endothelin receptors in astrocytes cultured from rat striata (Venance et al., 1998). In the single-cell model, the Ca²⁺ amplitudes computed for different relative receptor densities α₀ reproduce this behavior (Fig. 2). Agonist specificity of the response may be determined further by the G-protein used and by its coupling to PLC; cf. Equation 9.

Fig. 2.

Agonist response in the model of a single cell. Activation level was varied by changing the relative receptor density at saturating agonist dose. This translates into different activities of PLCβ (cf. Eq. 9). Shown are the Ca²⁺ responses in the presence (solid line) and absence (dashed line) of PLCδ. The duration of activation was 4 sec.

The presence of the kinetic term for Ca²⁺-activated PLCδ induces a sharp threshold in the dose–response curve for the calcium amplitude (Fig.2, solid line, at α₀ ∼ 10⁻³). The [Ca²⁺]_i amplitudes generated by the model are in the range of the experimentally observed values.

Agonist-evoked intercellular Ca²⁺ waves

In the experimental system, the focal administration of a sufficiently potent PLCβ-activating stimulus to a single astrocyte gave rise to an ICW (Venance et al., 1997). In the model, transient PLCβ activity in one cell initiates an ICW with the correct range of propagation (Fig. 3A). The pattern of [Ca²⁺]_i(cytoplasmic Ca²⁺ concentration) transients in the excited cells is in close agreement with the experimental data. The amplitude is largest in the stimulated cell and declines over a few cells to a plateau, at which it remains for a number of cells before failing abruptly (Fig. 3B). The speed of intercellular propagation is found to be determined primarily by the intercellular delays, as observed in the experiments. The average wave speed in the model for signal propagation through the first three rows of cells is in the same range as the speed computed from experimental data: 8–10 μm/sec and 15–20 μm/sec, respectively. In the model, the propagation speed between neighboring cells decreases as the distance from the stimulated cell increases. Interestingly, despite the good agreement of the overall time course and amplitude behavior between model and experiment, this speed decrease is at variance with at least some of the experimental data, showing a practically constant speed (Venance et al., 1997).

Fig. 3.

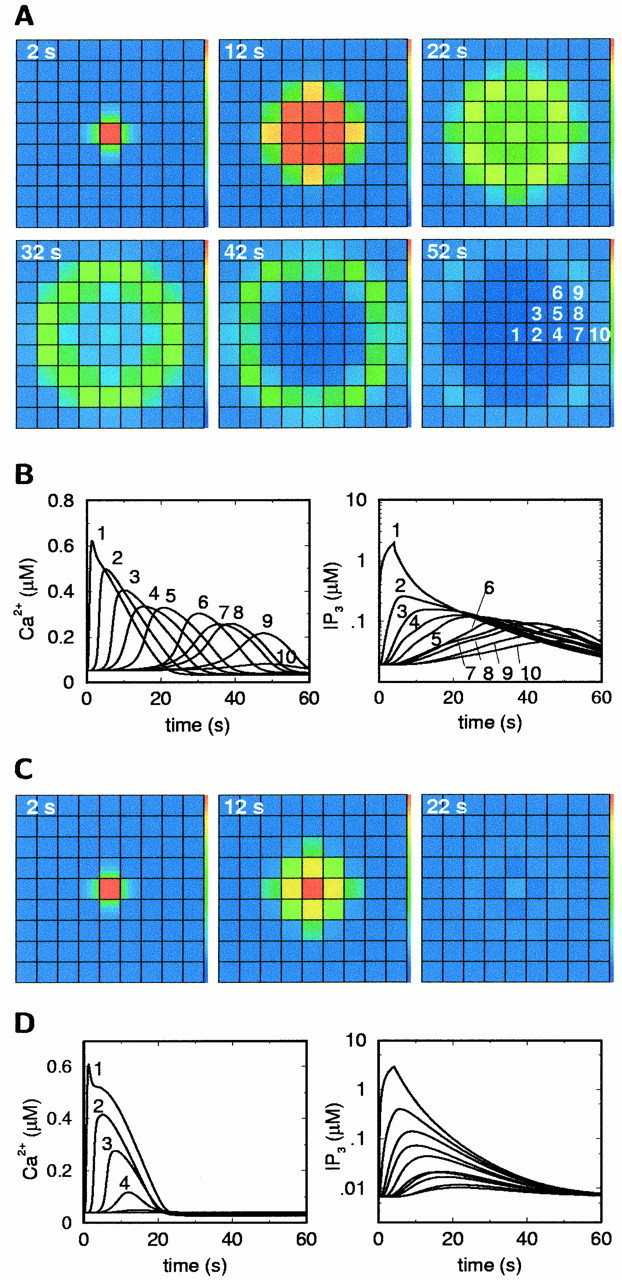
Intercellular Ca²⁺ waves in the model. A, [Ca²⁺] _isignal for the reference parameter set (Table 1). B, Time courses of [Ca²⁺]_i and IP₃ in the cells as labeled in the last frame ofA. C, [Ca²⁺]_i signal in the absence of Ca²⁺ activation of IP₃ production by PLCδ, under otherwise identical conditions. D, Time courses of [Ca²⁺]_i and IP₃corresponding to C. The central area of a simulated field of 19 × 19 cells is shown. The stimulus was an elevation of the PLCβ activity v₈ in the central cell to 1 μm/sec for 4 sec.

The model allows us to test hypotheses on the propagation mechanism. To discriminate between the roles of intercellular Ca²⁺ and IP₃diffusion, the gap-junctional permeability for Ca²⁺ was set to zero, and the IP₃ permeability was kept at its reference value. This modification has no significant effect on ICW propagation; the wave has practically the same appearance as shown in Figure3A. By contrast, zero IP3 permeability and reference Ca²⁺ permeability prevents ICW propagation (data not shown). Consequently, the intercellular propagation is based primarily on IP₃ diffusion.

A central question is whether the ICWs are mediated solely by IP₃ diffusion from the stimulated cell or whether the regeneration of IP₃ in downstream cells via PLCδ plays a role. If, under otherwise unchanged conditions, PLCδ activity is set to zero in every cell, the ICW range is greatly reduced: only the immediate neighbors of the stimulated cell respond with a significant [Ca²⁺]_i increase (Fig. 3C,D). Thus in the ICW depicted in Figure 3A, PLCδ acts as a signal amplifier in downstream cells. However, the regeneration of the signal is only partial, so that the ICWs fail after a finite distance, as is usually observed in Ca²⁺ imaging experiments (Giaume and Venance, 1998).

Regenerative versus diffusive intercellular Ca²⁺ signals

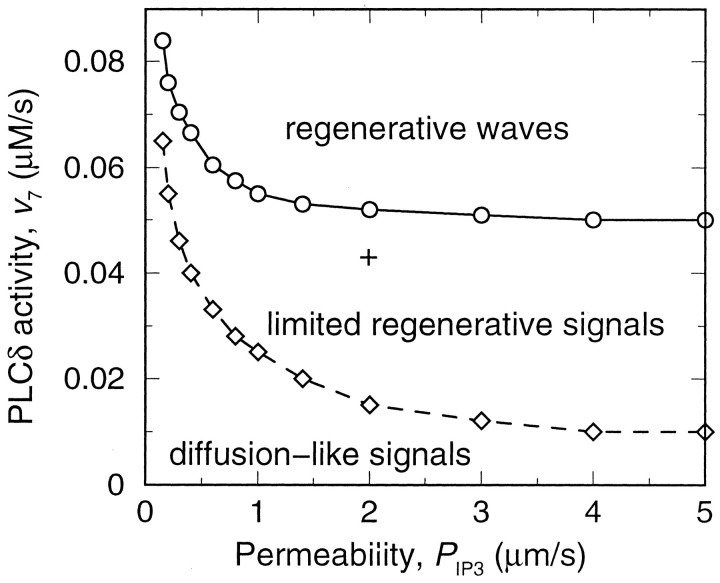
Such a partial regenerative behavior resulting in spatially limited waves may seem unexpected, given that regenerative phenomena (such as the spread of an action potential along an axon) do not normally exhibit an intrinsic spatial limit to propagation. To analyze this question, we studied the effects of variations in two crucial parameters: the PLCδ activity and the permeability of gap junctions, determining the signal regeneration and intercellular propagation, respectively. Three qualitatively different behaviors are obtained (Fig. 4). If PLCδ activity and gap-junctional coupling are sufficiently large, fully regenerative ICWs are observed. Such waves propagate with constant amplitude and speed over arbitrarily large distances (and correspond to traveling waves in the usual mathematical sense). Conversely, if PLCδ activity is set to very low levels, the intercellular Ca²⁺signals do not encompass more cells than when the signal is driven solely by IP₃ diffusion from the stimulated cell alone. Such signals are thus characterized as diffusion-like in the phase diagram. In between the parameter ranges giving rise to regenerative waves, on the one hand, and purely diffusive signals on the other, there is a region in the phase diagram in which signal regeneration by PLCδ noticeably increases ICW extent beyond the range observed in the diffusive mode, yet the overall range remains finite. The ICW of Figure 3A was calculated for parameters in this region, and we hypothesize that this limited regenerative mode of propagation is operating in cultured striatal astrocytes.

Fig. 4.

Types of intercellular signals in the model as a function of the gap junction permeability for IP₃ and the maximal activity of PLCδ. According to the spatial range of propagation, three qualitatively different behaviors are observed: diffusion-like signals, the range of which equals the range obtained by IP₃ diffusion from the stimulated cell alone; limited regenerative signals, for which the spatial range is increased by IP₃ regeneration yet remains finite; and regenerative waves without an intrinsic limit to their propagation. The + indicates the parameter values used for Figure 3, A andB. All parameters except P_IP3and v₇ are as in Figure 3. The upper boundary (solid line) is obtained by applying a small stimulus to one cell and evaluating whether it triggers a limited signal or develops into a wave with constant concentration profile. The lower boundary (dashed line) gives the parameter values at which the wave range is increased above the range achieved by pure IP₃ diffusion from the stimulated cell, for the same stimulus as in Figure 3.

A difference between the two boundary lines in Figure 4 must be noted. The location of the boundary between the regions of diffusion-like and limited regenerative ICWs (dashed line) depends somewhat on the strength of the initiating stimulus. The line shown is obtained for the stimulus strength used in the simulation of Figure 3. However, the lines for other stimulus strengths were found to lie very close to it. The upper boundary between limited regenerative and fully regenerative ICWs (Fig. 4, solid line) is independent of the stimulus strength (mathematically, it defines the parameters at which traveling wave solutions arise). The experimental data that are available agree with this latter observation to the extent that in cultures showing limited ICWs triggered by receptor agonist also the considerably more potent mechanical stimuli give rise to limited waves (Venance et al., 1997).

Differential control of the Ca²⁺ wave range by signal regeneration, propagation, and initiation

PLCδ activity

From Figure 4 it is clear that the parameters of signal regeneration and propagation have a decisive impact on the wave range. The wave range obtained on variation of PLCδ activity is shown in Figure 5A. The results were calculated for the same stimulus strength (i.e., PLCδ activity in the stimulated cell) as in Figure 3. Similar results are obtained for different stimulus strengths. The three regions of diffusion-like behavior (v₇ < 0.018 μm/sec), limited regenerative ICWs (0.018 μm/sec <v₇ < 0.055 μm/sec), and fully regenerative ICWs (v₇ > 0.055 μm/sec) are readily recognized.

Fig. 5.

Dependence of ICW range on the model parameters.A, Maximal activity of PLCδ; B, activity of SERCA pump; C, IP₃ permeability of the gap junctions; D, comparison of the effects of the three parameters. The reference conditions (0% parameter change) are as for Figure 3, A and B. All parameters that are not shown and the stimulation conditions are as in Figure 3.

Rate of Ca²⁺ release from the internal stores

Because in downstream cells Ca²⁺ and IP₃ are linked in a positive feedback loop during the upstroke of a Ca²⁺ signal, parameters influencing the IP₃-induced Ca²⁺ release can be expected to have a similar impact on ICW behavior as PLCδ activity does. This was tested for the Ca²⁺ load of the ER stores. Increasing the sarco/endoplasmic reticulum calcium ATPase (SERCA) activity k₃ results in a higher Ca²⁺ load of the ER in the rest state and, consequently, in a larger Ca²⁺discharge under otherwise unchanged activation conditions. This yields an increased range of ICWs (Fig. 5B). Again one observes regions of diffusion-like (k₃ < 0.25 sec⁻¹), limited regenerative (0.25 sec⁻¹ <k₃ < 0.65 sec⁻¹), and fully regenerative (k₃ > 0.65 sec⁻¹) ICW propagation.

Permeability of gap junctions

Increases in the gap-junctional permeability for IP₃ also yield increased wave ranges, but the qualitative dependence is different (Fig. 5C). For the reference parameters chosen, even large permeability increases result only in limited regenerative ICWs; a transition to fully regenerative behavior does not take place. The parameter diagram of Figure 4indicates that this is the typical situation, because the region of points for which an increase in the junctional permeability leads to a crossing of the boundary to regenerative waves is comparatively small (the solid border line runs almost parallel to the permeability axis for P_IP3 > 1 μm/sec). It is noteworthy that this model prediction agrees with recent experimental results by Rouach et al. (2000), comparing the extent of IWC propagation in astrocytes in the presence and absence of neurons. Significant increases in astrocytic gap junctional communication and in connexin 43 expression (∼50%) were observed in cocultures of astrocytes and neurons compared with pure astrocyte cultures. These were associated with a 30% increase in the number of cells excited by mechanically triggered ICWs.

Figure 5D provides a quantitative comparison of the effects of PLCδ activity, SERCA activity, and IP₃permeability on wave range. The reference point (0% parameter change) corresponds to the simulation of Figure 3A. This normalized plot shows that the wave range depends more strongly on the activities of the two enzymes than on the IP₃permeability.

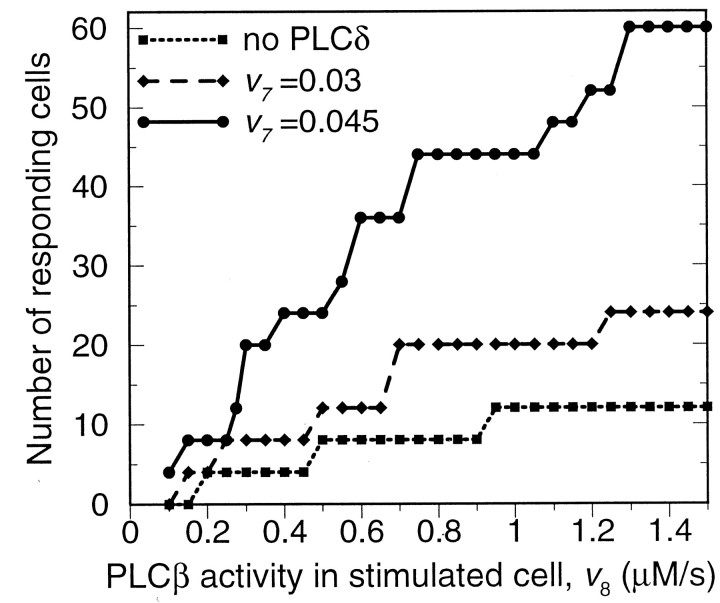
Strength of agonist stimulus

Within the regions of partially regenerative and diffusion-like ICWs, the stimulus strength is a crucial determinant of the spatial range of an ICW: larger stimuli yield larger ranges of propagation (Fig. 6). The sensitivity of the wave range toward the stimulus strength, as measured by the slope of curves in Figure 6, increases with PLCδ activity and thus with the partial regeneration of the signal. In the experiments, different stimulus strengths were naturally supplied by various receptor agonists (such as ET-1, Glu, carbachol, and methoxamine), giving rise to different calcium amplitudes in the stimulated cell. Indeed, the wave range was observed to correlate with the potency of the agonist (Venance et al., 1997). The ranges obtained in the model for limited regenerative ICWs (with PLCδ activities between 0.03 and 0.045 μm/sec) are in agreement with the experimental data.

Fig. 6.

Dependence of ICW range on the strength of the stimulus, as measured by the PLCβ rate in the stimulated cell.

Preferential pathways for ICWs

Although the model results agree well with salient experimental observations, they differ in a crucial respect of potential physiological relevance (see Discussion). Agonist-evoked ICWs in astrocyte cultures are considerably more irregular and follow preferential pathways (Finkbeiner, 1992; Venance et al., 1997; Giaume and Venance, 1998). Because of the symmetry of the model assumptions, such irregularity cannot be seen in the simulations. Thus we asked what kind of heterogeneity, if introduced in the model, results in preferential pathways for ICWs. Some irregularity of wave propagation must stem from the fact that cells do not form regular arrays. However, ICWs can appear as rather regular concentric waves, particularly if astrocytes are stimulated strongly by mechanical means (Venance et al., 1997; Giaume and Venance, 1998). This observation indicates that preferential pathways seen after focal agonist application are not governed solely by cell arrangement. In the following, we pursue the idea that variations in parameters between cells, i.e., in the expression levels of enzymes and/or connexins, may play a role. To elucidate the impact of such cellular heterogeneity, random variations of key parameters involved in the regeneration and propagation steps—the PLCδ activity, the SERCA activity, and the gap junctional permeability—are considered. To identify their individual effects, one parameter is distributed heterogeneously across the cells, whereas all others are kept at the same value in all cells.

For the distribution of PLCδ activity among the individual cells in astrocyte populations, no data are currently available. Simulations were performed with random variation of the PLCδ rate constant within the range resulting in limited regenerative ICWs (as given in Fig.5A) and log-normal distribution functions. For such variations, ICW propagation remained practically concentric. Similarly, random heterogeneity in the SERCA rate constant within the range yielding limited regenerative ICWs (Fig. 5B) did not yield substantial deviation from concentric wave shapes (data not shown).

By contrast, random variations of gap-junctional coupling gave rise to preferential pathways of ICW propagation (Fig.7). To obtain information on the distribution of the gap-junctional permeability in astrocyte cultures from rat striatum, gap-junctional conductance data obtained in a previous study were analyzed (Venance et al., 1995). The data show considerable heterogeneity of coupling (Fig. 7A), with a substantial portion of cell pairs being relatively poorly coupled (>40% of the cells have a conductance of <10% of the maximum value of 40 nS). A smooth cumulative distribution function fitted to these data was used to assign a random permeability value to each cell–cell interface in the model. The appearance of the ICWs in such a cell array is considerably closer to experimental observation, with a typical result depicted in Figure 7B. In this example, the wave propagates more readily in the vertical directions.

Fig. 7.

Effect of heterogeneous distribution of gap junction channels between cells on ICWs. A, Histogram of experimental data from double patch-clamp recordings of gap junction conductance in striatal astrocyte pairs (n = 24) [experiments as described in Venance et al. (1995)].B, ICW obtained for a random distribution of intercellular conductances drawn from the probability distribution obtained as a smooth fit to the data in A.

Thus the model exhibits different effects for random heterogeneity in propagation and regeneration steps. On the one hand, the ICWs obtained with heterogeneous intercellular coupling are consistent with the preferential pathways observed in cell culture. On the other hand, randomness in the parameters of regeneration steps does not have a comparable influence on ICW shape, presumably because differences in IP₃ regeneration are averaged to some degree between neighboring cells (provided that the cells are coupled sufficiently strongly). Thus far random heterogeneity was considered; however, the preferential distribution or activation of PLCδ along certain paths could strongly bias wave propagation along such paths in a controlled manner. In model simulations with such defined heterogeneous PLCδ distributions, we were able to obtain such effects (data not shown). Given the regulation of PLCδ activity by various external signals (cf. Rebecchi and Pentyala, 2000), such “regulated pathways” with a high degree of plasticity could be established by the molecular mechanisms considered in the model.

Refractory period

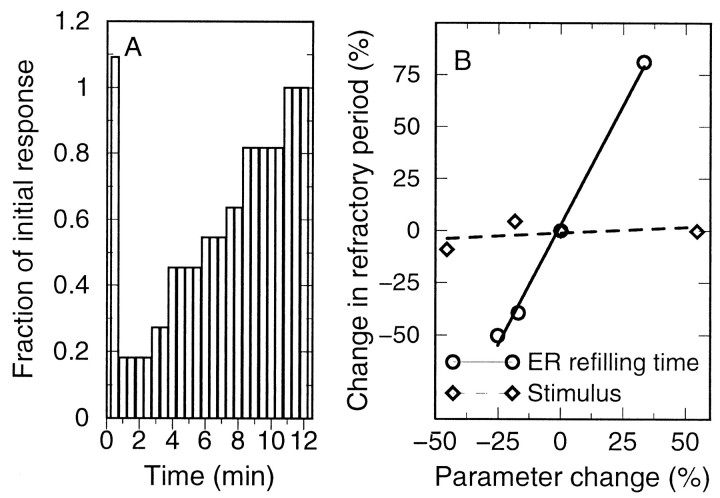
In vivo, astrocytes may be subjected to multiple neurotransmitter stimuli. The response characteristics under such conditions should be especially important in the context of astrocyte–astrocyte and astrocyte–neuron communication. To obtain some insight into this interaction process, double stimulation by agonist application to the same astrocyte was considered in the model. As a measure of the wave range, the number of cells responding to the second stimulus normalized by the number of initial responders is used. Simulations show a slight potentiation of the response when the second stimulus is given up to 30 sec after the first and thereafter show a marked refractory period on the time scale of several minutes (Fig.8A). When the second stimulus was applied to a neighbor of the initially stimulated cell, the refractory behavior was very similar (data not shown), demonstrating that it is caused by the dynamics of the entire field of cells.

Fig. 8.

Refractory period of the ICWs. A, For the parameters and stimulation conditions of Figure 3,A and B, a second stimulus of equal magnitude was applied to the same cell after the time indicated, and the fraction of the wave range compared with the range of the initial signal (44 responding cells) was measured. When the second stimulus was applied within 30 sec after the initial stimulus, a slight potentiation of the response is seen; for longer intervals, the system is refractory. B, Effect of Ca²⁺ store refilling time and stimulus strength on the refractory period. The reference conditions (0% parameter change) are as for Figure 3,A and B.

To obtain a quantitative measure, we define the refractory time τ_R by the expression:

$${\tau }_R=\underset{0}{\overset{\infty }{\int }}(1-N(t)/N_0)\text{dt},$$ Equation 12

where N₀ andN(t) denote the number of cells responding to the first stimulus and to a subsequent stimulus given at time tafter the first one, respectively. The definition (Eq. 12) is a convenient way of assigning a “half-life” to a monotonic transition process (Llorens et al., 1999), such as the recovery of full responsiveness of the astrocyte field. Using this formula, the refractory periods obtained under different conditions can be readily compared. In particular, we asked which processes control the value of τ_R. Inspecting the individual time courses of the model variables, one finds that only the Ca²⁺ concentration in the ER stores shows a pronounced slow transient on the time scale of several minutes, which is related to the refilling of the stores after the Ca²⁺ discharge. A store refilling time τ_S can be computed by an expression analogous to Equation 12 [when N(t) andN₀ are replaced by the Ca²⁺ concentration in the store at timet and at steady state, S(t) andS₀, respectively]. Assuming that there is no Ca²⁺ efflux from the ER other than the leak flux, which holds for most of the recovery phase, one obtains, after some algebra:

$${\tau }_{\text{s}}=\frac{k_1+k_3+k_5}{\beta k_1{k}_5}.$$ Equation 13

For the reference parameter set, there is a good agreement between store refilling time τ_S and refractory period τ_R of 4.17 and 4.95 min, respectively (note that identical numerical values are not to be expected because they require an unlikely linear relation between the wave range and the degree of ER store refilling). Moreover, by calculating the refractory period for different refilling times, under otherwise unchanged conditions, a strong positive correlation is obtained (Fig.8B, open circles). By contrast, the strength of the initiating stimulus itself has a comparatively minor influence on the refractory period (Fig. 8B,open diamonds).

DISCUSSION

Mechanistic studies of ICWs in astrocytes have shown that propagation can proceed through two pathways: gap junction channels and a diffusible extracellular signal (for review, see Charles and Giaume, 2002). We took advantage of the dominance of the gap-junctional pathway in rat striatal astrocytes and of the detailed experimental data available for this system to construct a mathematical model specifically for ICW propagation through gap junction channels. However, we will argue below that general conclusions derived from the model may also apply to the extracellular pathway. The model supports the hypothesis that, in astrocytes, IP₃ is the major component carrying the signal through gap junctions between cells. IP₃ is assumed to be produced in the cell stimulated directly with metabotropic receptor agonist through activation of PLCβ and by a Ca²⁺-activated mechanism in downstream cells, which do not experience the agonist. Ca²⁺-induced IP₃generation may be caused by PLCδ, which is activated by physiological Ca²⁺ concentrations. Its preferential expression within the CNS in astrocytes (cf. Rebecchi and Pentyala, 2000) could thus be linked to the role as a local signal enhancer in ICWs. Salient experimental findings are reproduced by the model: the typical amplitudes of the Ca²⁺ responses in successive cells, the overall magnitude of the wave speed, the control of the speed primarily by the intercellular delays, the spatial range of wave propagation, and the sensitive dependence of this range on the strength of the agonist stimulus. In the model, the distributions of gap junctions in the plasma membrane of a cell and of ER calcium stores were assumed to be spatially uniform. It would be an interesting extension to study the effect of subcellular spatial heterogeneities of these structures as reported e.g., by Paemeleire et al. (2000).

Any mechanism for ICWs based on signal regeneration must be compatible with the observed finite range of signaling in the astrocyte cultures studied so far. The prime example of a regenerative process in the nervous system, the propagation of an action potential along an axon, provides an appropriate point of reference. The hallmark of an action potential is the nondecremental behavior of speed and amplitude: at each node along the axon, the action potential triggers a depolarizing ionic flux sufficient to elicit an action potential at the following node. Therefore, the mechanism of propagation has no intrinsic range limit. In the model presented here, the mechanisms of signal regeneration can result, in a certain parameter region, in an analogous nondecremental, or fully regenerative, type of propagation for ICWs (see Fig. 4). Adjacent to it, there exists a parameter region in which regeneration of the signal occurs, yet the ICW range is limited. Accordingly, we propose the term “limited regenerative signaling” for this mode of ICW propagation. Interestingly, a limited regenerative propagation was also noted for action potentials in particular circumstances, especially when a neuron was stimulated before full recovery of excitability after an action potential (Katz, 1966). Limited regeneration in the model of ICWs can chiefly be understood as follows. The influx of IP₃ into a cell through gap junctions initiates a Ca²⁺ spike, inducing IP₃ production. However, IP₃ generation is of such a magnitude that the IP₃ efflux into the following cells is invariably smaller than the influx. There is thus a decline of IP₃ production from the stimulated cell outward, until the signal eventually fails. Interestingly, the model suggests that the gap-junctional IP₃ permeability is limiting to propagation only in a rather small region of parameter space [for P_IP3 < 1 μm/sec (Fig.4); cf. also analytical results on ICWs in discretely coupled cells (Höfer et al., 2001)] and that the main control over the wave range is exerted by the regenerative steps.

A previous model of ICW propagation from a focal stimulus postulates passive diffusion of IP₃ from the stimulated cells as the underlying process (Sneyd et al., 1994, 1995), and there is good experimental evidence that a point source of IP₃ can induce ICWs (Braet et al., 2001). This model is essentially obtained when PLCδ activity is set to zero in the present model (Fig. 3C,D). However, crucial properties of the astrocytic ICWs were found in the model only when IP₃ regeneration was included: (1) the reproduction of realistic wave ranges of up to 100 cells for realistic Ca²⁺ amplitudes in the stimulated cell; (2) the sensitivity of the wave range to the stimulus amplitude (again for realistic variations of the Ca²⁺amplitude as a measure of stimulus strength); and (3) the Ca²⁺ amplitude plateau and subsequent abrupt failure of propagation that has also been a prominent feature in the experimental data (Venance et al., 1997). These observations argue in favor of a regenerative component in the propagation mechanism.

Experimental findings indicate that regenerative mechanisms could be involved in ICWs also in other astroglial systems. Harris-White et al. (1998) have described self-sustained spiral ICWs in hippocampal slice cultures. Spiral waves are known to be a characteristic pattern of wave propagation in regenerative two-dimensional systems. Indeed, we could obtain spiral ICWs in preliminary simulations of the model when parameter values in the fully regenerative range were chosen (compare Fig. 4). In another study, incubation of astrocyte cultures with glucocorticoids was reported to increase the [Ca²⁺]_i baseline, which resulted in considerably larger ranges of ICWs (Simard et al., 1999). Our model indeed predicts for increased basal [Ca²⁺]_i that both the Ca²⁺ concentration in the stores and the basal activity of PLCδ rise, and, accordingly, a larger ICW range is obtained [in the experimental paper by Simard et al. (1999), involvement of ATP secretion is invoked, but this may follow a similar mechanism; see below].

These observations raise the question regarding to what extent the conclusions of our model can be generalized. It has been reported that calcium elevation alone does not generate ICWs in astrocytes, thus arguing against a calcium-activated component in IP₃ production (Leybaert et al., 1998). However, in the striatal system, ICWs can be evoked by focal stimulation of calcium influx through ionomycin, which per se increases the rate of IP₃ production (Venance et al., 1997). Thus the mechanism proposed in the model could be differentially expressed in various glial systems. ICW propagation via the extracellular pathway involves altogether different molecular mechanisms, including ATP release (Cotrina et al., 1998; Guthrie et al., 1999; Scemes et al., 2000) independent of calcium (Wang et al., 2000). Recent studies have also indicated regeneration of ATP during ICW propagation (Newman, 2001; Schipke et al., 2002). In this case, the principle of limited regenerative ICWs may apply to the extracellular pathway too. ATP in the extracellular pathway would then play a role analogous to IP₃ in the gap-junctional pathway. Because ATP acts on metabotropic receptors, its putative regeneration would be expected to include the regeneration of IP₃. This may provide a mechanism for the interaction of the gap-junctional and extracellular pathways.

In the context of the integration of astrocytic calcium signaling with other signaling processes in the CNS, besides its spatial properties its temporal characteristics are also relevant. Calcium spikes with a duration of seconds are considerably slower than action potentials. Moreover, the model predicts that a yet longer time scale, on the order of minutes, is introduced by the refractory period. Because the rate of ER Ca²⁺ store refilling turns out to be an important determinant of the refractory period, processes that act on store Ca²⁺ dynamics are potential modulators of the refractory period. These model predictions are open to experimental testing. Moreover, it can be hypothesized that differences from cell to cell in refractory behavior also contribute to the observed heterogeneity of cellular Ca²⁺ responses with respect to single spikes versus oscillations (Finkbeiner, 1992; Blomstrand et al., 1999).

The restricted range of ICWs could imply that information coded by Ca²⁺ changes in astrocytes has a specific field of interaction with neurons. In neuronal populations, selectivity of synaptic connections and synaptic efficacy are key elements in the drawing of neuronal networks. In astrocytic networks, the topographic patterns caused by gap junctional communication are less clear. Indeed, dye injection in various brain structures (cortex, hippocampus, striatum) indicates that passive diffusion occurs according to the concentric zone of coupling without any respect to frontiers of brain structures and compartmentalization (Konietzko and Muller, 1994;D'Ambrosio et al., 1998; Hamon et al., 1999). However, “geographic” properties and plasticity in astrocytic networks may not be determined by passive diffusion but could instead be caused by variations in other parameters affecting ICW propagation, most notably those involved in signal regeneration. In the model, the activities of PLCδ and SERCA are such determinants of signal regeneration. Thus the control of these processes may introduce selectivity in information processing by glial cells. Secondarily, astrocytic networks drawn by ICWs could also selectively affect neuronal networks, because close interaction occurs at synaptic contacts through the recently described tripartite synaptic constellation (Araque et al., 1999; Haydon, 2001).