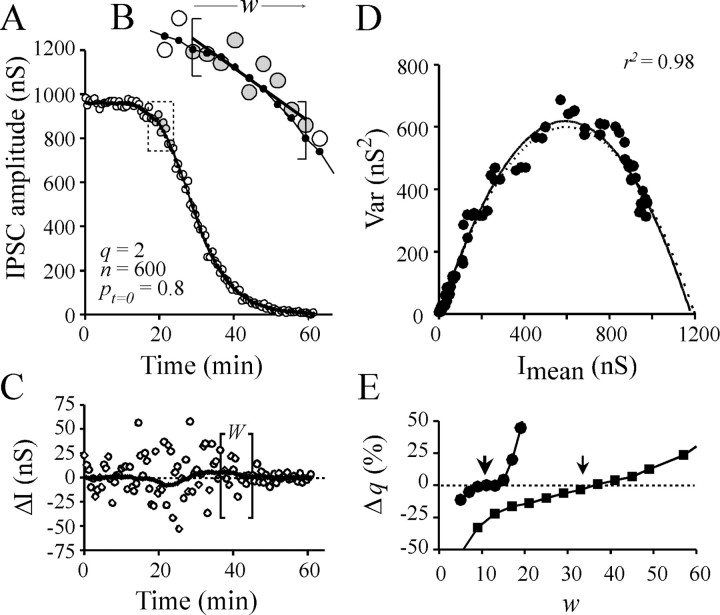
Fig. 1.

Determination of quantal parameters by nonstationary analysis as tested on a simulated experiment.A, IPSC amplitude =f(t) values (○) were calculated as the product binomial (n,p_t)*q in whichn = 600 sites and q = 2 nS. A sigmoid decrease of release probability p = p_o*p_A with time, t, was simulated using equationp_t = 0.8/[1 + exp(−(t−20)/−3.5)^0.5]. The solid line denotes the set of the I_meanvalues determined at each t (for details see Materials and Methods). B, Magnification of boxshown in A. The window width used for local linear fitting (w) is indicated withinbrackets (here w = 9). Linear fit is indicated by solid straight line. The mid-values of the local linear fits are the estimates of I_meanand are indicated by small dots on a solid line. C, Fluctuations in IPSC amplitude are approximated at each time t of the I= f(t) plot, by subtractingI_mean from corresponding Ivalue (○). The I_mean values determined by nonstationary analysis deviate from the trueI_mean. This difference was determined by subtracting the determined I_mean values from the predicted I_mean and is represented by asolid thick line. The brackets denote the window width W used for Var determination (hereW = 16). D, The corresponding Var = f(I_mean) plot. Solid line denotes the adjustment of the data by simple parabola (Eq. 4). The predicted parabola (dashed line) was calculated using Equations 1 and 2 and the above-mentioned quantal parameters. The difference between both parabolas generates errors in the determinations of qand n. The extent of this error can be minimized by optimizing the window width (w) used for local linear fitting of IPSC =f(t). Error in estimation ofq is shown in E[Δq(%)] as a function of w, for two “experimental” conditions: when simulated IPSC amplitude decreases rapidly (t_1/2 = 25 min) or slowly (t_1/2 = 75 min). These situations are denoted by ● and ▪, respectively. For these two conditions, optimalw values are indicated by arrows.