Fig. 5.

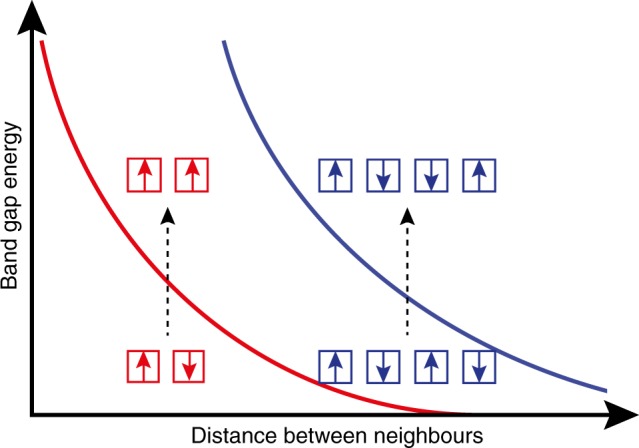
Relation between energy gap and spatial gap. The energy gap (solid lines) between magnonic eigenstates (modes) of coupled particles decreases with the particle distance and depends on the number of particles involved in the modes. The arrows indicate the phase of the oscillating magnetic moment in each particle (squares). The red curve shows the band gap between the antiparallel oscillation mode and the parallel oscillation mode, i.e., same phase versus opposite phase resonance. The analog in a continuous system would be the transition between a uniform mode and a mode where the wavelength is equal to the length of the system. The blue curve shows the band gap between an antisymmetric short-wavelength mode (lower blue squares) and a symmetric mode with twice the wavelength (upper blue squares). Closely spaced particles (which have stronger dipolar coupling) exhibit larger spectral gaps between such modes than distant particles do. The discontinuous nature of the particle chain discretizes the modes in k-space, such that these spectral gaps in the collective eigenmode spectrum are also band gaps