Fig. 1.

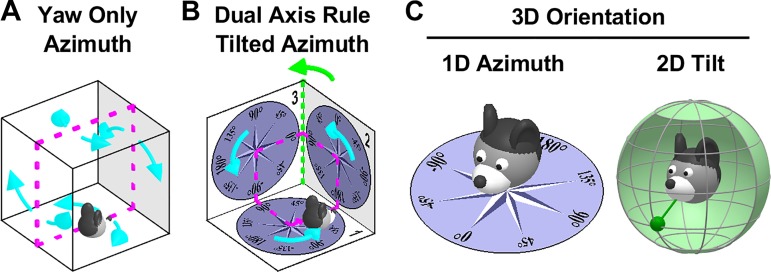
Fundamental differences between the Yaw-only (YO) and tilted azimuth (TA) models. A: the YO azimuth model (Calton and Taube 2005; Shinder and Taube 2019) assumes that vertical surfaces are treated as extension of the floor. Azimuth is computed by integrating yaw (i.e., left/right, cyan) rotations only, irrespective of the allocentric orientation of the locomotion surface. This model is sufficient to track head orientation when walking on the floor, ceiling, and opposite walls of a cage (magenta). B: the difference between the YO and TA (Laurens and Angelaki 2018)/dual-axis rule (Page et al. 2018) model arises when movement is not restricted to 2D. In this example, the animal completes a closed-loop trajectory (magenta) that includes three left-hand yaw turns (cyan). The YO model cannot maintain allocentric consistency, as it will only register a total azimuth rotation angle of 270°, in contradiction with the fact that the animal has returned to its initial orientation. The “missing” rotation not registered by the YO model occurs when the animal transitions from surface 2 to 3 (green). This is the 2nd axis of the dual-axis rule: Tracking 3D orientation correctly requires updating azimuth also when the locomotion surface (or the head-horizontal plane) crosses vertical surfaces, i.e., during rotations about an earth-vertical axis. The equivalent TA model (Laurens and Angelaki 2018; see Fig. 3A for definition) assumes that azimuth is measured in the compasses drawn on the three surfaces and yields a correct total rotation of 360°. Thus, the YO model of Shinder and Taube (2019) and the TA/dual-axis model of Page et al. (2018) and Laurens and Angelaki (2018) are consistent with each other only when movement is restricted to 2D (e.g., magenta trajectory in A). The YO model would fail to track azimuth during 3D movements (as shown in B; see also Laurens and Angelaki 2018). Thus, by supporting the YO model, Shinder and Taube (2019) imply that the HD system will fail during 3D movements on the surfaces of a cube, which is inconsistent with experimental results (Page et al. 2018). C: decomposition of 3D orientation into 1D tilted azimuth and 2D tilt, as proposed by Laurens et al. (2016) and Laurens and Angelaki (2018). Azimuth measures 1D orientation relative to allocentric horizontal landmarks and has a circular topology. Tilt measures 2D orientation of the head relative to gravity, or equivalently the egocentric orientation of the gravity vector (left: green pendulum) and has a spherical topology. This model generalizes Finkelstein's toroidal (Yaw-Pitch) model (Finkelstein et al. 2015) to 3D.