The Effects of Reverse Causality and Selective Attrition on the Relationship Between Body Mass Index and Mortality in Postmenopausal Women

Abstract

Concerns about reverse causality and selection bias complicate the interpretation of studies of body mass index (BMI, calculated as weight (kg)/height (m)²) and mortality in older adults. The objective of this study was to investigate methodological explanations for the apparent attenuation of obesity-related risks in older adults. We used data from 68,132 participants in the Women’s Health Initiative (WHI) clinical trial for this analysis. All of the participants were postmenopausal women aged 50–79 years at baseline (1993–1998). To examine reverse causality and selective attrition, we compared rate ratios from inverse probability of treatment– and censoring–weighted Poisson marginal structural models with results from an unweighted adjusted Poisson regression model. The estimated mortality rate ratios and 95% confidence intervals for BMIs of 30.0–34.9, 35.0–39.9 and ≥40.0 were 0.86 (95% confidence interval (CI): 0.77, 0.96), 0.85 (95% CI: 0.72, 0.99), and 0.88 (95% CI: 0.72, 1.07), respectively, in the unweighted model. The corresponding mortality rate ratios were 0.96 (95% CI: 0.86, 1.07), 1.12 (95% CI: 0.97, 1.29), and 1.31 95% CI: (1.08, 1.57), respectively, in the marginal structural model. Results from the inverse probability of treatment– and censoring–weighted marginal structural model were attenuated in low BMI categories and increased in high BMI categories. The results demonstrate the importance of accounting for reverse causality and selective attrition in studies of older adults.

The nature and shape of the relationship between body mass index (BMI) and mortality in older adults is a frequently debated topic in the epidemiologic and clinical literature. Several papers have demonstrated decreasing relative risks of high BMI in older adults, suggesting that the relationship between high BMI and mortality is either null or slightly protective (1–3). Numerous hypotheses have been suggested to explain the altered BMI-mortality relationship in older adults, including both physiological and methodological explanations (4, 5). Questions about the relationship between BMI and mortality are particularly salient in older women because the proportion of individuals with BMI over 30 (calculated as weight (kg) divided by height (m) squared) is higher in women than in men (40% vs. 35%) and life expectancy is greater for women than men (6, 7). We examined the influence of reverse causality and selection bias on the relationship between BMI and mortality, using data from a large cohort of postmenopausal women in the United States, the Women’s Health Initiative (WHI).

REVERSE CAUSALITY

Reverse causality is defined as a phenomenon in which the outcome precedes and causes the exposure (8–10). Technically, using a strict definition of reverse causality, it is not possible to have reverse causality in studies with all-cause mortality as the endpoint. Experiencing the outcome (mortality) prior to exposure measurement, or having mortality cause exposure, is impossible. However, in the context of obesity-mortality research, the term reverse causality is often used to refer to a situation in which disease status affects both exposure and outcome, because disease often causes weight loss and disease increases mortality risk. Despite being called reverse causality, this is actually a concept that fits the standard definition of confounding in epidemiology (see Figure 1A–C) (10, 11). This is why, in the context of obesity-mortality studies, the phrase reverse causality is often used interchangeably with the terms “confounding by preexisting disease” or “confounding by illness-related weight loss” (8, 10, 12). Throughout this discussion, we use the term reverse causality to refer to a concept that most epidemiologists would call confounding, but we are referring to it as reverse causality for consistency with the obesity literature.

Figure 1.

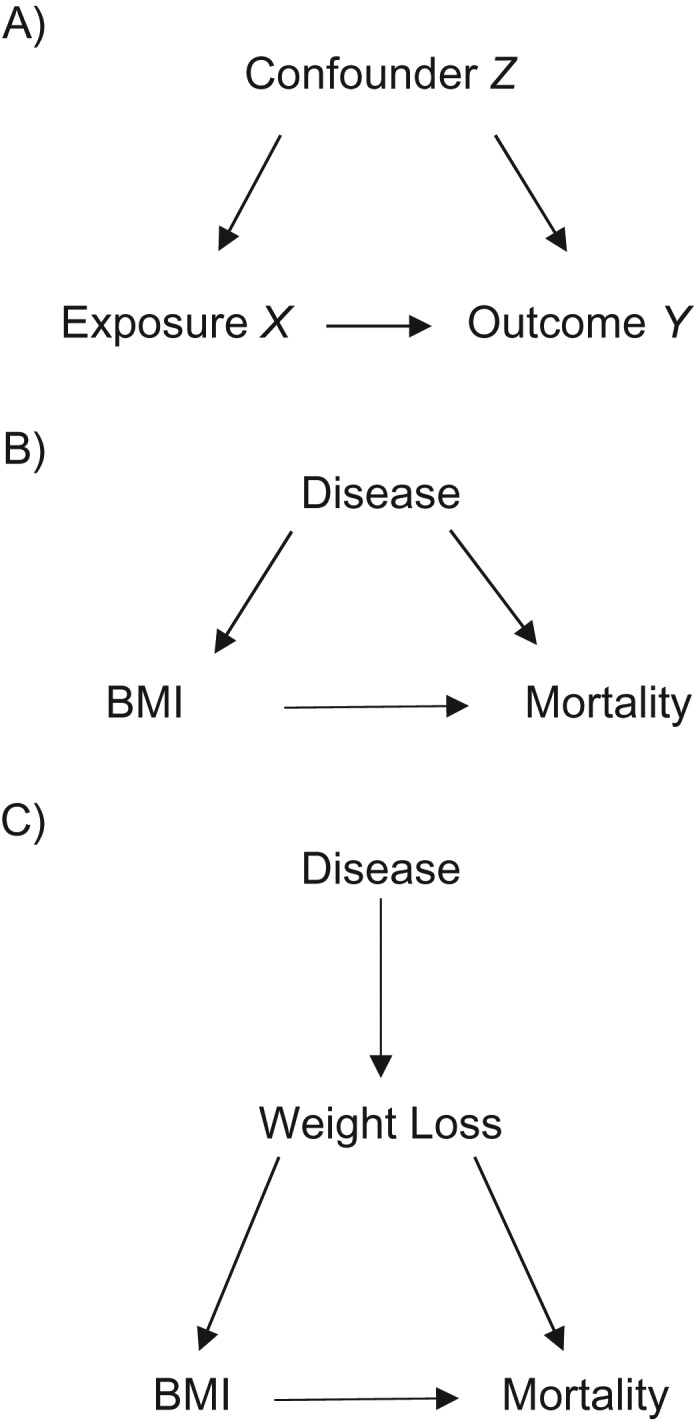
Causal diagrams depicting a generic confounding scenario (A), confounding due to preexisting disease (B), and confounding due to illness-related weight loss (C). In all these situations, the confounding variable is associated with the exposure and a risk factor for the outcome. BMI, body mass index.

There are 2 common techniques to assess the possible impact of reverse causation in obesity research: 1) excluding individuals with prevalent disease at baseline and 2) excluding deaths that occur early in the follow-up period. The rationale for the first technique comes from a long-standing tradition in observational epidemiology, that individuals must be free of disease at baseline. It is now recognized that such exclusions can, in certain cases, introduce bias (13–15). It is well-known that obesity leads to cardiovascular disease and many types of cancer; thus, excluding individuals with these prevalent conditions at baseline amounts to conditioning on a variable affected by exposure (16). Therefore, while some authors seek to use exclusions to explore reverse causality, it is likely inducing a different form of bias (17).

There is a slightly different rationale for the second type of exclusion, deleting deaths that occur early in the follow-up period. This type of exclusion is intended to mitigate the concern that subclinical illness leads to weight loss and then death early in follow-up. If subclinical and then clinical disease cause weight loss, lower BMI categories will be composed of a disproportionate number of individuals with disease at cohort entry (10). Excluding early deaths is an attempt to control for the influence of subclinical disease; because we cannot control for undiagnosed illness using statistical techniques, early deaths are used as a proxy measure (18). A number of studies have demonstrated that excluding early deaths fails to account for illness-related weight loss, or reverse causality (10, 18, 19). As Allison et al. concluded, “If excluding early deaths resulted in elimination of all diseased subjects, and no nondiseased subjects, the bias would be eliminated. However, this outcome seems quite unlikely to be achieved . . .” (18, p. 673). Excluding early deaths is unlikely to control for bias as intended and results in substantial reductions in sample size.

Instead of relying on restrictions or exclusions, statistical methods have been developed to control for time-varying confounding affected by prior exposure, such as marginal structural models (8, 20, 21). In this context, the time-varying confounder is disease status: Obesity is a cause of disease, being ill affects body weight, and both obesity and disease increase mortality risk (Figure 2) (22). Disease status is on the causal pathway from obesity to mortality; thus, using conventional adjustment techniques, such as regression adjustment or restriction, might bias the estimated effect of obesity on mortality (13, 23). It is not possible to estimate the obesity-mortality relationship using standard statistical approaches because failing to account for disease status will result in a biased effect estimate, but adjusting for disease status will also result in a biased estimate (13).

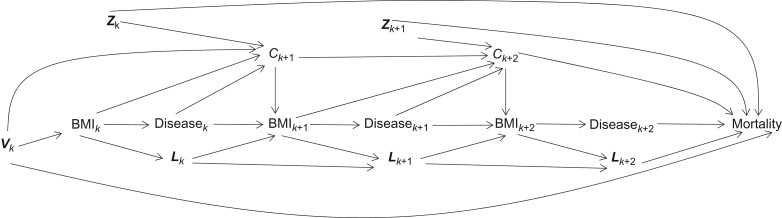
Figure 2.

Directed acyclic graph for the effect of body mass index (BMI) on mortality. V_k is a vector of baseline covariates and L_k is a vector of time-varying covariates of BMI and mortality. Subscript k represents the baseline the Women’s Health Initiative clinic visit, k + 1 represents visit 1, and k + 2 represents visit 2. C represents censoring and Z represents a vector of time-varying covariates that influence both censoring and mortality. This directed acyclic graph is a simplified representation of these relationship for 2 Women’s Health Initiative (United States, 1993–2005) clinic visits, but similar relationships exist for the entire range of follow-up visits.

SELECTIVE ATTRITION

Selective attrition, a form of selection bias, is a second hypothesized explanation for the attenuated relationship between obesity and mortality in older adults (13, 24). Selective attrition produces selection bias when the losses to follow-up are influenced by the exposure of interest and the outcome, or by determinants of the exposure and the outcome. This is a particular concern in studies of obesity in older adults because obesity predicts disease risk, which is strongly associated with attrition and mortality (24). This is depicted in Figure 2. To account for differential attrition, we use inverse probability of censoring weights (IPCW) (13, 20, 24). IPCW were developed to correct for selection bias using measured determinants of attrition and the outcome of interest (25). The goal of using IPCW is to recreate the study population that we would have observed had there been no censoring, upweighting existing observations to account for those who are missing.

Our objective was to understand the influence of reverse causality and selection bias on the relationship between BMI and mortality in postmenopausal women. We compared the results from an inverse probability–weighted marginal structural model with results from a conventionally adjusted model to add to our understanding of the magnitude and direction of these sources of bias in aging research.

METHODS

Study population

We used data from 68,132 participants in the Women’s Health Initiative (WHI) clinical trials in this analysis. The WHI is a cohort of postmenopausal women recruited between ages 50 and 79 years from 40 clinical centers across the United States (26–28). The WHI clinical trials (1993–2005) were focused on the effects of hormone therapy, dietary modification, and vitamin supplementation on health outcomes in postmenopausal women. Detailed information about recruitment has been published elsewhere (26, 27, 29). During the active trial phase, clinic visits were required semiannually and consisted of questionnaires and interviews focused on symptom reporting and management, compliance, and safety. Once per year, participants’ anthropometric measurements were recorded, including height and weight (26). We chose to study the participants in the WHI clinical trials, as opposed to the entire WHI cohort, which includes an additional 93,676 women in an observational study, because the annual anthropometric measures provide valuable information about weight change and disease status. Women in the WHI observational study did not have annual in-person follow-up visits. The study protocol was reviewed by institutional review boards at each clinical center as well as the WHI coordinating center (30).

Assessment of endpoints

The primary outcome of interest in this analysis is all-cause mortality up until the end of the core WHI study follow-up (March 31, 2005). Mortality was ascertained through annual mail and telephone contacts, searches of medical record and death certificates, and the National Death Index (30). Follow-up for primary clinical endpoints (cardiovascular events, cancer, fracture) occurred every 6 months during the WHI trials and were adjudicated by trained physicians (27). Diagnosis of cardiovascular disease included angina, coronary revascularization, coronary heart disease, carotid endarterectomy/angioplasty, stroke, transient ischemic attack, heart failure, and myocardial infarction. Diagnosed fracture included any adjudicated fracture of hip, leg (including knee), pelvis, foot/ankle, tailbone, spine, arm (including elbow), and shoulder. Diagnosed cancer included all cancer types except nonmelanoma skin cancer.

Assessment of exposure and covariates

BMI was measured annually during the active study phase for all WHI clinical trial participants. BMI is an index of weight for height, calculated as weight in kilograms (kg) divided by height in meters (m) squared. For this analysis, participants were categorized into standard BMI groups: ≤18.5, 18.5–24.9, 25.0–29.9, 30.0–34.9, 35.0–39.9, and ≥40.0. Information on relevant confounding variables was collected at baseline and annual study visits, either through questionnaires or in-clinic measurements. Baseline confounders of the BMI-mortality relationship include age, trial participation (hormone therapy, dietary modification), trial arm (intervention or not), race/ethnicity, education, marital status, income, health insurance, and smoking history (pack-years). Time-varying confounders were measured throughout the follow-up period. Time-varying confounders in this analysis include disease status (cardiovascular disease, cancer, fracture), hormone therapy use, smoking status, self-rated health status, physical activity level, alcohol intake, physical functioning, hypertension, and diabetes.

Statistical analysis

Our primary analysis focused on understanding the influence of reverse causality and selection bias on the BMI-mortality relationship. We first used generalized linear models with a log link and a Poisson distribution to obtain unweighted adjusted rate ratios for each BMI category compared with the reference category, BMI 25.0–29.9. BMI 25.0–29.9 was used as the reference group because it is the group associated with the lowest risk of mortality and less likely to be affected by illness-related weight loss than BMI 18.5–24.9 (31–33). BMI 25.0–29.9 is also the largest group, and using it as the reference provides the most stable results. The Poisson parameter is a collapsible effect estimate and thus can be compared with results from a marginal structural model (34). The number of days between WHI clinic visits was included as an offset term. All analyses were performed using Stata, version 14 (StataCorp LLC, College Station, Texas).

We then fit the parameters of a marginal structural model in a 2-step process: estimating inverse probability weights and then using the weights to approximate the parameters of a marginal structural model. Estimating inverse probability of treatment weights (IPTW) accounts for time-varying confounding by variables affected by prior exposure and estimating IPCW accounts for differential attrition. We estimated the weights using pooled logistic regression and used stabilized weights to improve statistical efficiency (20, 35, 36). Due to the large range of the IPTW for BMI, we truncated the weights at the 1st and 99th percentile. This decision was made understanding the bias-variance tradeoff associated with weight truncation (20). For each individual, IPTW are the inverse of the probability of being in each BMI category at each follow-up visit, conditional on observed time-fixed and time-varying variables:

$$S{W}_{ij}^X=\prod _{k=0}^{j}f\frac{f[x_{ik}|{\overline{\mathbf{x}}}_{\mathbf{i}\mathbf{k}-1},V_{i0},C_{ik}=0]}{f[x_{ik}|{\overline{\mathbf{x}}}_{\mathbf{i}\mathbf{k}-1},{\overline{\mathbf{L}}}_{\mathbf{i}\mathbf{k}-1},C_{ik}=0]}$$

X _ik represents individual i’s BMI category measured at visit k, with the start of follow-up at visit k = 0; ${\stackrel{}{X}}_{ik-1}$ represents individual i’s BMI measured at the previous cohort visit. Overbars represent covariate history up to and including visit k. ${\overline{\mathbf{L}}}_{\mathbf{i}\mathbf{k}-1}$ is a vector of baseline and time-varying covariates measured for individual i at visit k − 1. The variables included in L are age, cohort, smoking status, physical activity, alcohol consumption, physical functioning, cardiovascular disease, hypertension, diabetes, cancer, and any fracture. Values of time-varying covariates included in L were from the prior cohort visit. Implicit in this weighting model is the Markov assumption that the individual’s probability of exposure at visit k depends on their history of the time-varying covariates included in ${\overline{\mathbf{L}}}_{\mathbf{i}\mathbf{k}-1}$. Following the assumptions encoded in our directed acyclic graph, probability of exposure at visit k depends on the history of the time-varying covariates included in ${\overline{\mathbf{L}}}_{\mathbf{i}\mathbf{k}-1}$ only through the most recent value ${\mathbf{L}}_{\mathbf{ik}-1}$ (20, 24, 37). V_i0 is a subset of L_i, a vector of variables measured at baseline (visit k = 0), including trial participation and arm, race/ethnicity, education, marital status, health insurance status, self-rated health, pack-years smoked, and prior hormone therapy use. C_ik = 0 indicates that individual i was not censored by visit k (i.e., to be included in the IPTW model for visit k, individual i still had to be part of the study cohort). We explored numerous additional functional forms for the pooled logistic model used to estimate the IPTW, including product terms for interaction between BMI and disease status variables, restricted cubic splines for BMI and age with 4 knots, and a broader set of covariates (including the use of a continuous variable for systolic and diastolic blood pressure, number of years since menopause, age at menarche, age at menopause, hysterectomy status, specific fracture types, differing types of hormone use, and more detailed information about smoking history, such as pack-years). However, the alternative specifications did not appreciably alter study results.

IPCW are the inverse of the probability of remaining in the study cohort (i.e., uncensored) at each follow-up visit:

$$C{W}_{ij}^X=\prod _{k=0}^{j}f\frac{\mathrm{Pr}[C_{ik}=0|{\overline{\mathbf{C}}}_{\mathbf{i}\mathbf{k}-1}=0,X_{ik},V_{i0}]}{\mathrm{Pr}[C_{ik}=0|{\overline{\mathbf{C}}}_{\mathbf{i}\mathbf{k}-1}=0,X_{ik},{\overline{\mathbf{Z}}}_{\mathbf{i}\mathbf{k}-1}]}$$

Where the denominator is the probability that participant i is not censored by visit k, conditional on individual i not being censored at a previous clinic visit, BMI category at visit k, and a defined set of baseline and time-varying covariates that influence censoring and mortality (Z_ik−1). Accounting for selective attrition using IPCW requires that we identify a complete set of confounders of censoring and mortality (38). For individual i, the numerator of the IPCW is the conditional probability of remaining alive and uncensored up to visit k, given that they had not been censored between visits k − 1 and k, their exposure status at visit k (X_ik), and a vector of baseline covariates (V_i0) that are a subset of Z_ik.

Finally, using the product of the IPTW and IPCW as an analytical weight, we fit marginal structural models with a robust variance estimator to estimate the adjusted effects of BMI on mortality. Baseline confounders of the BMI-mortality relationship (V) were included in the final marginal structural model, given that they had been previously included in the numerator of the stabilized weight models (39). The final Poisson marginal structural model, including the offset term log T_i, was:

$$\log (\mathrm{E}\left(Y|X\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}X+B_{k}V+\log T_i$$

As a secondary analysis, we investigated the influence of baseline age on the relationship between BMI and mortality. In this analysis, we included a product term for interaction between baseline age cohort (A; 50–59 years, 60–69 years, or 70–79 years) and BMI (X) in the marginal structural model (40, 41):

$$\log (\mathrm{Pr}\left(\mathit{Y}|\mathit{X}\right)={\mathrm{\beta }}_0+{\mathrm{\beta }}_1\mathit{X}+{\mathrm{\beta }}_2\mathit{A}+{\mathrm{\beta }}_3\mathit{XA}+B_4\mathit{V}$$

The results from this supplemental analysis allowed us to calculate stratum-specific effects and examine whether the relationship between BMI and mortality differed among women who were younger versus older at cohort entry.

RESULTS

Demographic characteristics of the study population at baseline are presented in Table 1. There were 5,310 women in the estrogen-alone trial, 8,506 women in the estrogen-and progestin trial, and 19,541 women in the dietary-modification trial. Mean BMI was consistent across age strata, but there were interesting differences in the proportions of women in specific BMI categories according to age at baseline. The proportion of women in the lower 3 BMI groups (<18.5, 18.5–24.9, 25.0–29.9) increased across age strata, while the proportion of women in the higher 3 BMI groups (30.0–34.9, 35.0–39.9, ≥40.0) decreased across baseline age strata. Of the 68,132 women in the WHI clinical trials, there were 3,769 deaths (5.5%) up to the end of the core WHI trial follow-up in 2005, an average of 8.6 years of follow-up. As expected, a greater proportion of women who died were older at baseline: By the end of follow-up, 720 women (2.6%) who were aged 50–59 years had died, 1,750 women (5.8%) who were 60–69 years had died, and 1,299 women (12.3%) who were 70–79 years had died.

Table 1.

Baseline Demographic Characteristics of Participants in the Women’s Health Initiative Clinical Trials, United States, 1993–1998

Characteristic	Total Cohort, % (n = 68,132)	Age Group, years
		50–59 (n = 27,408), %	60–69 (n = 30,193), %	70–79 (n = 10,531), %
Age, yearsa	62.1 (7.0)	55.2 (3.0)	64.7 (2.8)	73.1 (2.3)
Race/ethnicity
Non-Hispanic white	81.7	76.9	83.8	87.8
Non-Hispanic black	10.3	12.7	9.2	6.9
Hispanic	4.2	6.1	3.4	1.7
Other	3.8	4.3	3.5	3.6
Education
Some high school	5.6	4.76	5.8	7.2
High-school diploma or equivalent	18.5	15.4	20.9	19.6
Postsecondary school	50.0	50.9	49.2	50.3
Postgraduate school	25.9	29.0	24.1	22.9
Smoking status
Current smoker	7.9	10.4	7.1	4.1
Former smoker	41.0	40.6	42.0	39.1
Never smoker	51.1	49.0	51.0	56.8
Marital status
Married	60.9	65.5	61.7	47.2
Widowed	17.1	6.9	18.8	38.5
Divorced	16.3	20.5	14.9	9.7
Had health insurance	93.8	89.7	95.6	99.5
Employed	39.4	65.0	27.4	10.4
History of CVD	19.0	13.6	20.6	28.6
BMI categoriesb
<18.5	0.43	0.36	0.42	0.62
18.5–24.9	26.9	27.2	25.6	30.2
25.0–29.9	35.7	33.7	36.5	38.6
30.0–34.9	22.3	22.2	22.9	21.3
35.0–39.9	9.9	10.8	10.1	7.2
≥40.0	4.7	5.8	4.5	2.1
BMIa,b	28.9 (5.9)	29.2 (6.2)	29.0 (5.8)	27.9 (5.2)
Years since menopausea	14.4 (9.0)	8.1 (6.4)	16.4 (7.3)	24.7 (7.0)

Abbreviations: BMI, body mass index; CVD, cardiovascular disease.

^a Values are expressed as mean (standard deviation).

^b Weight (kg)/height (m)².

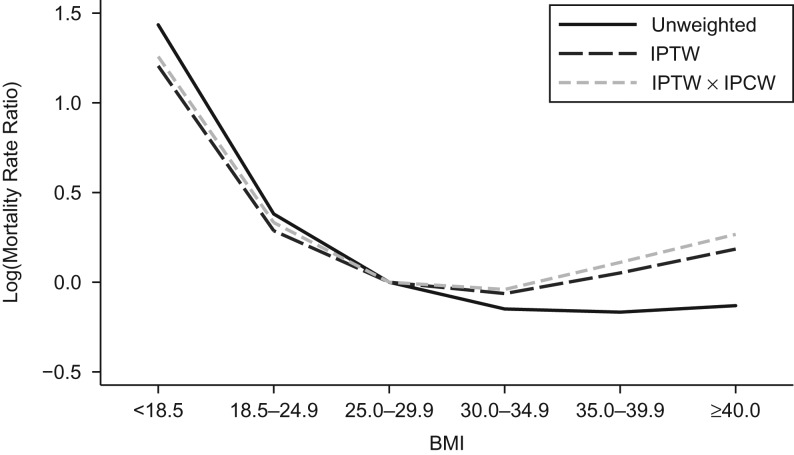
The primary study results are illustrated Figure 3, comparing results from an unweighted Poisson regression model and 2 marginal structural models, one weighted by IPTW and the second weighted by the product of the IPTW and IPCW. The mean of the weights was 0.99 (SD, 0.07) and ranged from 0.61 to 1.41. At low BMI levels (<18.5 and 18.5–24.9), IPTW and IPCW attenuated the mortality rate ratio compared with the unweighted regression results. Adding IPCW to the IPTW-weighted marginal structural model resulted in no change in estimates, indicating no influence of selective attrition at low BMI levels. At high BMI levels (30.0–34.9, 35.0–39.9, and ≥40.0), including IPTW and IPCW resulted in increased rate ratios. Resulting values from an IPTW-weighted marginal structural model were higher than from the unweighted model, and adding IPCW to the model further increased estimates.

Figure 3.

Graphical comparison of log mortality rate ratio results from unweighted, inverse probability of treatment–weighted (IPTW) and IPTW × inverse probability of censoring–weighted (IPCW) marginal structural model, Women’s Health Initiative cohort, United States, 1993–2005.

Numeric results comparing the mortality rate ratios and 95% confidence intervals from unweighted adjusted and marginal structural models are presented in Table 2. Compared with those for BMI 25.0–29.9, rate ratios from the multivariate adjusted unweighted model were 4.20 (95% confidence interval (CI): 3.22, 5.48) for BMI <18.5, 1.46 (95% CI: 1.32, 1.62) for BMI 18.5–24.9, 0.86 (95% CI: 0.77, 0.96) for BMI 30.0–34.9, 0.85 (95% CI: 0.72, 0.99) for BMI 35.0–39.9, and 0.88 (95% CI: 0.72, 1.07) for BMI ≥40.0. Corresponding estimates from the marginal structural model weighted by IPTW and IPCW were: 3.51 (95% CI: 2.57, 4.44) for BMI <18.5, 1.39 (95% CI: 1.26, 1.54) for BMI 18.5–24.9, 0.96 (95% CI: 0.86, 1.07) for BMI 30.0–34.9, 1.12 (95% CI: 0.97, 1.29) for BMI 35.0–39.9, and 1.31 (95% CI: 1.08, 1.57) for BMI ≥40.0.

Table 2.

Incidence Rate Ratios for the Effect of Body Mass Index on Mortality Among Postmenopausal Women in the Women’s Health Initiative Clinical Trials, United States, 1993–2005

BMIa	Adjusted, Unweighted Resultsb		IPTW-Weighted Marginal Structural Modelc		IPTW × IPCW Weighted Marginal Structural Modelc
	IRR	95% CI	IRR	95% CI	IRR	95% CI
<18.5	4.20	3.22, 5.48	3.34	2.61, 4.25	3.51	2.57, 4.44
18.5–24.9	1.46	1.32, 1.62	1.33	1.21, 1.46	1.39	1.26, 1.54
25.0–29.9	1.0	Referent	1.0	Referent	1.0	Referent
30.0–34.9	0.86	0.77, 0.96	0.94	0.85, 1.04	0.96	0.86, 1.07
35.0–39.9	0.85	0.72, 0.99	1.05	0.92, 1.20	1.12	0.97, 1.29
≥40.0	0.88	0.72, 1.07	1.20	1.01, 1.43	1.31	1.08, 1.57

Abbreviations: CI, confidence interval; BMI, body mass index; IPCW, inverse probability of censoring weights; IPTW, inverse probability of treatment weights; IRR, incidence rate ratio.

^a Weight (kg)/height (m)².

^b The unweighted model adjusted for baseline covariates plus time-varying confounders (age, trial arm, race/ethnicity, education, marital status, income, health insurance status, smoking status and history, disease status (cardiovascular disease, cancer, fracture), hormone therapy use, self-rated health, physical activity level, alcohol intake, physical functioning, hypertension, and diabetes).

^c Adjusted only for baseline covariates (age, trial participation and assignment arm, race/ethnicity, education, marital status, income, health insurance status, and smoking status and history).

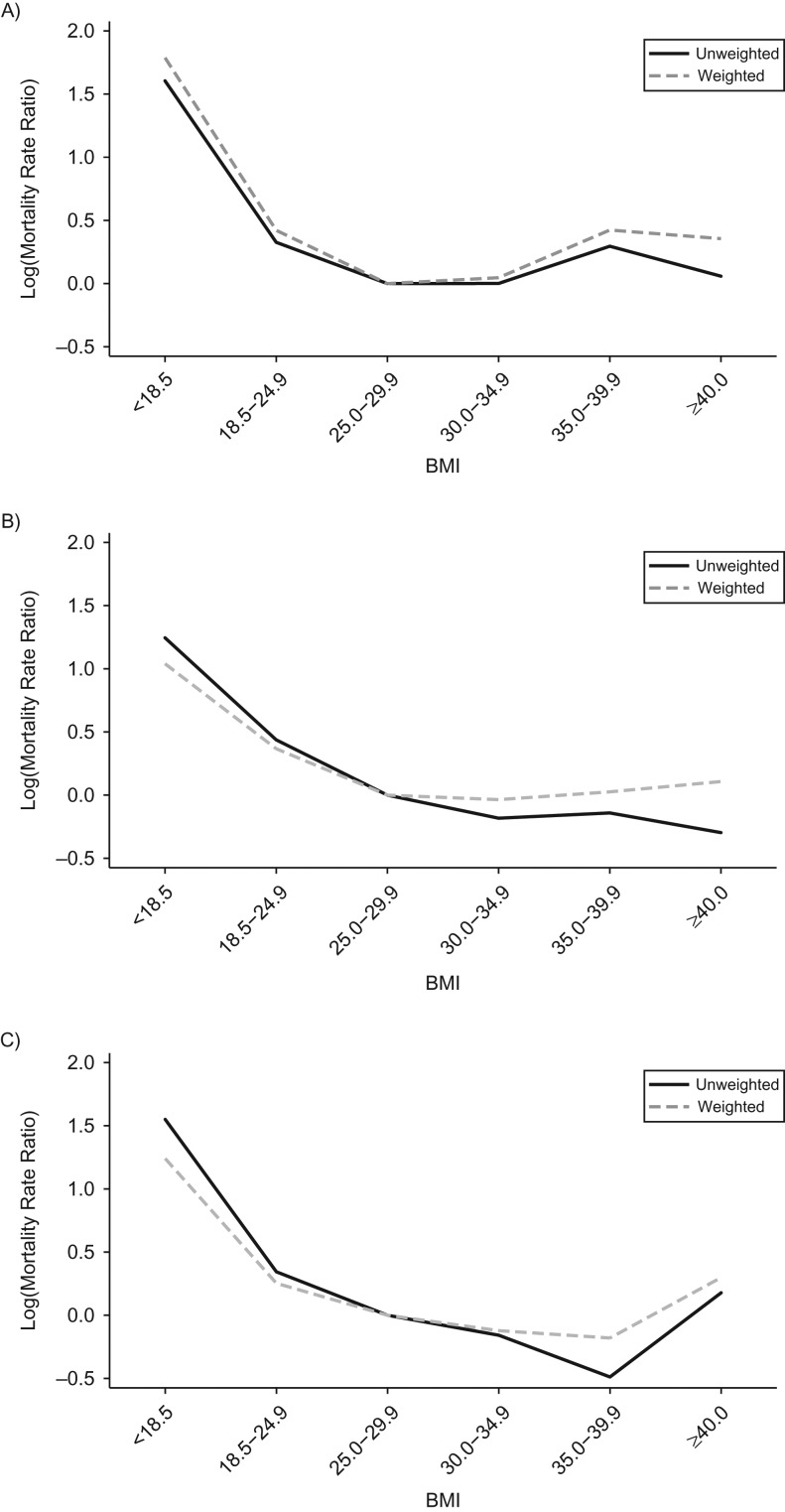
Results from secondary analyses stratified by baseline age cohort are presented in Table 3 and Figure 4, comparing mortality rate ratio estimates for an unweighted model and a marginal structural model with IPTW and IPCW. In women who were 50–59 years of age at baseline, results from the marginal structural model were greater than results from the unweighted adjusted model in all of the BMI categories. In the youngest age group, results from the marginal structural model indicated an elevated risk at low BMI (<18.5 and 18.5–24.9) and high BMI (35.0–39.9 and ≥40.0) compared with BMI 25.0–29.9. In the oldest age group, 70–79 years, comparing results from the unweighted adjusted and marginal structural model indicated differing effects in the low and high BMI categories. In the low BMI categories, the results from the marginal structural model were lower than the results from the unweighted adjusted model, but in the high BMI categories, results from the marginal structural model were higher than results from the unweighted adjusted models.

Table 3.

Incidence Rate Ratios, Stratified by Age Group at Baseline, for the Effect of Body Mass Index on Mortality in Postmenopausal Women in the Women’s Health Initiative Clinical Trials, United States, 1993–2005

Age Group and BMIa	Adjusted, Unweighted Resultsb		IPTW × IPCW Weighted Marginal Structural Modelc
	IRR	95% CI	IRR	95% CI
50–59 years
<18.5	5.17	2.07, 8.28	5.97	3.27, 10.91
18.5–24.9	1.44	1.08, 1.81	1.52	1.18, 1.97
25.0–29.9	1.0	Referent	1.0	Referent
30.0–34.9	0.96	0.71, 1.21	1.05	0.80, 1.37
35.0–39.9	1.17	0.84, 1.52	1.53	1.13, 2.06
≥40.0	0.91	0.59, 1.24	1.43	1.00, 2.05
60–69 years
<18.5	3.42	1.91, 4.93	2.83	1.80, 4.44
18.5–24.9	1.53	1.30, 1.76	1.44	1.24, 1.68
25.0–29.9	1.0	Referent	1.0	Referent
30.0–34.9	0.85	0.71, 0.99	0.96	0.82, 1.14
35.0–39.9	0.88	0.71, 1.07	1.03	0.83, 1.26
≥40.0	0.80	0.58, 1.02	1.11	0.85, 1.46
70–79 years
<18.5	4.80	2.92, 6.67	3.46	2.29, 5.22
18.5–24.9	1.41	1.17, 1.65	1.29	1.10, 1.51
25.0–29.9	1.0	Referent	1.0	Referent
30.0–34.9	0.83	0.66, 1.00	0.86	0.73, 1.07
35.0–39.9	0.59	0.40, 0.77	0.84	0.62, 1.12
≥40.0	1.27	0.78, 1.77	1.35	0.89, 2.05

Abbreviations: CI, confidence interval; BMI, body mass index; IPCW, inverse probability of censoring weights; IPTW, inverse probability of treatment weights; IRR, incidence rate ratio.

^a Weight (kg)/ height (m)².

^b The unweighted model adjusted for baseline covariates plus time-varying confounders (age, trial arm, race/ethnicity, education, marital status, income, health insurance status, smoking status and history, disease status (cardiovascular disease, cancer, fracture), hormone therapy use, self-rated health, physical activity level, alcohol intake, physical functioning, hypertension, and diabetes).

^c Adjusted only for baseline covariates (age, trial participation and assignment arm, race/ethnicity, education, marital status, income, health insurance status, and smoking status and history).

Figure 4.

Comparison of results from an unweighted model with adjustment and inverse probability of treatment–weighted (IPTW) and inverse probability of censoring–weighted (IPCW) marginal structural models for women who were 50–59 years old (A), 60–69 years old (B), and 70–79 years old (C) at baseline, Women’s Health Initiative cohort, United States, 1993–2005.

DISCUSSION

Using prospectively collected data from the WHI clinical trials, we fitted inverse probability–weighted marginal structural models to examine the influence of reverse causality and selective attrition on the BMI-mortality relationship in postmenopausal women. The final weighted model demonstrated the mortality risks associated with being either in the low (<18.5 and 18.5–24.9) or high (35.0–39.9 and ≥40.0) BMI categories compared with having a BMI of 25.0–29.9. There was no strong evidence of an increased mortality risk for women with BMI 30.0–34.9.

Results highlight that the influence of reverse causality and selection bias differs in low and high BMI categories. In the total cohort, in the low BMI categories, using an IPTW marginal structural model resulted in attenuated effect estimates, relative to an unweighted model with adjustment, and minimal change when IPCW were included in the model. These results support the hypothesis that the lower BMI categories are composed of individuals who have experienced disease-related weight loss. Accounting for the confounding by disease status using an IPTW marginal structural model resulted in a lower mortality rate than a standard model with adjustment. We did not find evidence that selective attrition influenced the BMI-mortality relationship in the low BMI categories.

In high BMI categories, using an IPTW marginal structural model resulted in greater effect estimates than in the unweighted model with adjustment, and adding IPCW to the model further increased the mortality rate. These findings support our 2 main hypotheses regarding the influence of reverse causality and selective attrition: Illness-related weight loss biases the relative risks downward in high BMI categories, because individuals who have experienced disease-related weight loss are less likely to be in the high BMI categories, thus leaving an artificially “healthy” group in the high BMI categories (10). Also, individuals with high BMI are more likely to drop out of a study, and also have a higher mortality risk, artificially attenuating effect estimates (42). After accounting for these 2 sources of downward bias, we saw the mortality rate ratio increase, which is consistent with prior research on reverse causality and selection bias (24, 25, 43, 44). It is important to note that the confidence intervals for the unweighted and weighted models were largely overlapping. This makes it difficult to draw a definitive conclusion about the potential influence of reverse causality in this analysis.

We also presented results from analyses stratified by baseline age cohort. The stratified results demonstrated notable differences in the BMI-mortality relationship in women who were older versus younger at cohort entry. The unweighted, stratified results are consistent with previous research in the WHI, demonstrating attenuated risks among women who were 70–79 years old at cohort entry compared with those who were 50–59 or 60–69 years old (1, 3). There are several plausible explanations for these findings, including selective survival, birth cohort effects, and effect measure modification, or, in all likelihood, a combination of these potential explanations. In research on older adults, there is a concern that obese individuals might experience premature mortality, dying prior to cohort entry and leaving a selected study sample of survivors to be enrolled into the analytical cohort. Survival up to cohort entry is recognized as an important form of selection bias known as selective survival (13, 45, 46). Selection bias due to selective survival is a challenging methodological concern when studying obesity in older adults (47).

Weuve et al. (48) report that this form of selective survival could be responsible for apparent “muting” of certain risk factors in older ages, whereby harmful risk factors appear less detrimental. Our results are consistent with this hypothesis but do not preclude other plausible explanations. This bias is structurally similar to the type of selection bias discussed by authors examining the relationship between cigarette smoking and dementia risk, a situation in which it is nearly impossible to claim any real benefit of exposure (24, 47). Unlike cigarette smoking, biological explanations for beneficial effects of BMI in old age might be plausible, but selection bias is also a reasonable explanation. Stratifying on age at cohort entry is one approach that can be used to understand and compare the obesity-related mortality risk among individuals who are different ages at cohort entry (baseline age). In this context, stratification does not eliminate the influence of selective survival, but could help us to understand it better. Simulation methods exist (44, 49) to quantify the magnitude of bias under scenarios that mimic the real-life survival experience of a cohort of older adults, and it is possible to use an estimand such as the “survivor average causal effect” that theoretically applies to individuals who would have survived to old age, regardless of exposure status (46). However, when seeking to understand the effect of obesity in a real-life cohort of older adults, neither approach fully answers the question of interest. It is difficult to provide a single explanation for why the BMI-mortality relationship differs across age strata because the reasons for these differences are complex and multifactorial, including both biological and methodological factors.

In addition to the use of marginal structural models, other methods have been suggested to control for reverse causality or confounding by disease status, including using weight histories, lifetime maximum BMI, instrumental variables, or Mendelian randomization studies (43, 50–54). Although the rationale and assumptions for each approach vary, the underlying theory is that these methods are techniques for understanding the effect of BMI on mortality in later life, unconfounded by illness related weight loss. For instance, in the case of instrumental variables, offspring BMI has been used as an instrument for an individual’s own BMI, because offspring BMI is highly correlated with parental BMI, and an illness (i.e., cancer) that might affect parental BMI would not simultaneously affect offspring BMI (51). Mendelian randomization is an extension of this concept, whereby genetic variants are used as an instrumental variable to estimate the effect of BMI on mortality because disease status would have no influence on an individual’s genetic makeup (53). Using lifetime maximum BMI is a different approach, where individuals are asked to recall their highest adult weight, and that is used as an exposure variable in analyses in place of current weight. This approach is appealing because it identifies an individual’s BMI status in adulthood prior to any illness-related weight loss (43). Finally, other approaches leveraging weight histories include studies with repeated measures of BMI starting in early adulthood, ostensibly capturing the direct influence of changes in BMI, and potentially illness-related weight loss, on mortality (54).

There are several assumptions required to estimate causal effects from observational data. We assumed the model was correctly specified, that there was no unmeasured confounding (exchangeability assumption), no measurement error, and that the positivity assumption was satisfied (20). A limitation of our results is a potential violation of the consistency assumption (55, 56). One of the key identifiability assumptions for causal inference requires that interventions be well-defined; BMI is not a well-defined intervention because there are numerous ways for an individual to be assigned to their actual BMI (57, 58). It is possible to imagine several interventions that could affect an individual’s BMI (e.g., a diet and/or exercise program, medication), and each of these interventions might be associated with a different counterfactual outcome (57, 59). Cole and Frangakis (56) expand on the standard version of consistency to allow for multiple routes for a particular treatment to be assigned, where consistency is defined as $Y_j^{obs}=Y_j\left(x,k\right)\mathrm{if}x=X_j$, no matter the value of k. This definition assumes that for any individual the exposure is only from the route observed for that individual (56). Other authors, such as VanderWeele and Hernán, have also discussed estimating causal effects when there are multiple versions of treatment (58, 60). An interesting direction for future work would be a simulation study and sensitivity analysis examining the effect of a series of different specifications for BMI as an exposure. If the results demonstrated that the effect of BMI on mortality is consistent across specifications, it would be evidence to support Cole and Frangakis’s definition of consistency (56).

The goal of this paper was to examine reverse causality and selection bias in the context of BMI-mortality studies in postmenopausal women. The strengths of the present work include a large, well-characterized cohort with detailed follow-up information and outcome ascertainment. Using methods from the causal inference literature, we avoided excluding individuals at baseline, deaths that occur early in the follow-up period, or making any unrealistic assumptions that censoring is ignorable. Given that the WHI cohort includes only women, further research is needed on this topic to explore differences by sex, as well as race or ethnicity (61). Another limitation is that the use of BMI to accurately characterize adiposity in postmenopausal women has been questioned (5, 62). BMI might be a less reliable indicator of adiposity in older women due to physical changes that occur after menopause and loss of lean muscle mass (63). This might have introduced some nondifferential exposure misclassification into our analysis (63). Despite these limitations, the conclusions from this study provide insight into common methodological concerns for researchers studying the effects of BMI in older adults. Our study highlights the mortality risk associated with having a very low or high BMI in postmenopausal women, which runs counter to the prevailing conclusion that BMI is a “less important” mortality risk factor in older adults.

Abbreviations

BMI

body mass index

IPCW

inverse probability of censoring weights

IPTW

inverse probability of treatment weights

WHI

Women’s Health Initiative