Abstract
Sparse representation-based brain functional network modeling often results in large inter-subject variability in the network structure. This could reduce the statistical power in group comparison, or even deteriorate the generalization capability of the individualized diagnosis of brain diseases. Although group sparse representation (GSR) can alleviate such a limitation by increasing network similarity across subjects, it could, in turn, fail in providing satisfactory separability between the subjects from different groups (e.g., patients vs. controls). In this study, we propose to integrate individual functional connectivity (FC) information into the GSR-based network construction framework to achieve higher between-group separability while maintaining the merit of within-group consistency. Our method was based on an observation that the subjects from the same group have generally more similar FC patterns than those from different groups. To this end, we propose our new method, namely “strength and similarity guided GSR (SSGSR)”, which exploits both BOLD signal temporal correlation-based “low-order” FC (LOFC) and inter-subject LOFC-profile similarity-based “high-order” FC (HOFC) as two priors to jointly guide the GSR-based network modeling. Extensive experimental comparisons are carried out, with the rs-fMRI data from mild cognitive impairment (MCI) subjects and healthy controls, between the proposed algorithm and other state-of-the-art brain network modeling approaches. Individualized MCI identification results show that our method could achieve a balance between the individually consistent brain functional network construction and the adequately maintained inter-group brain functional network distinctions, thus leading to a more accurate classification result. Our method also provides a promising and generalized solution for the future connectome-based individualized diagnosis of brain disease.
Keywords: Alzheimers disease, mild cognitive impairment, resting-state functional magnetic resonance imaging (rs-fMRI), functional connectivity, brain functional network, group sparse representation, diagnosis
1. Introduction
Alzheimer’s disease (AD) is an irreversible serious neurological disease in the elderly population, mainly characterized by progressive perceptive and cognitive deficits [1]. As a prodromal stage of AD, mild cognitive impairment (MCI) has attracted increasing attention since more than half of MCI subjects will progress to dementia in about five years [2]. Timely detection of MCI before converting to AD is fundamentally important and clinically valuable for effective intervention and possible treatment. Computer-aided individual diagnosis of brain diseases has been increasingly studied due to the progress in modern neuroimaging and computing techniques [3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. However, accurate MCI diagnosis is still considerably challenging because of subtle functional and anatomical changes in MCI subjects compared with normal aging people. A promising technique for sensitively capturing such subtle changes is constructing the whole-brain functional connectivity (FC) networks (or brain connectome) based on the resting-state functional magnetic resonance imaging (rs-fMRI) and extracting the connectome-based features for classification. To this end, the FC is typically calculated for each pair of brain regions by measuring the temporal synchronization of their blood oxygenation level-dependent (BOLD) signals [13, 14], resulting in a whole-brain FC network characterizing the intrinsic functional organization of the brain [15, 16, 17, 18]. With many successful applications for other brain diseases [19, 20, 21], the whole-brain FC network has been extensively demonstrated to be more sensitive than the anatomical metrics for early AD diagnosis [22, 23, 24, 25, 26, 27, 28].
While promising, most of the previous functional network studies have utilized simple FC metrics, e.g., Pearson’s correlation (PC)-based temporal synchronization between two brain regions [29, 30]. Despite of its simplicity and biological intuitiveness, PC bares a major drawback of modeling only the pairwise linear interactions, without accounting for more complex influences among multiple brain regions. To overcome this limitation, sparse representation (SR) [31, 32, 33] or similar methods such as graphical Lasso [34, 35], were adopted for constructing a sparse brain functional network by considering multiple regions’ effects. With SR, the BOLD signals of a brain region can be represented by a linear combination of the signals from a small number of other brain regions, and the estimated combination weights can be regarded as the FCs. However, due to data-driven nature in SR and other similar methods, a potential issue is that the constructed brain functional network in the individual level inevitably leads to the relatively large inter-subject variability in the topographical structure of the networks due to the unpredictable (but individually different) interferences of imaging noises and artifacts. This could lead to a consequence of poor generalization ability for the subsequently trained classifier due to the inhomogeneity or inconsistency across subjects, and more problematically, produce the unsatisfactory MCI diagnosis accuracy since the subtle FC changes in MCIs compared to the controls are likely to be overwhelmed by such large inter-subject variability [36].
By the enforcement of imposing a common sparsity structure across all subjects, the population-based prior-constrained graphical Lasso has been developed to reduce such inter-subject variability for constructing the group consistent individual brain functional networks [37]. Aiming to increase the inter-subject comparability, group sparse representation (GSR) has also been proposed by jointly estimating the FC (i.e., representation weights) for all subjects using a group Lasso constraint with l2,1-norm [36], which encourages the joint selection or deletion of certain connectivity links for all the subjects. GSR provides an effective way to alleviate the concern of the inter-subject variability; however, it also raises another concern in the opposite direction, i.e., it may sacrifice the between-group separability (e.g., separability between the patient and control groups) due to excessive enforcing of a similar network topographical structure for all the subjects, ignoring that fact subjects are from group. For MCI diagnosis, this will become a disadvantage since the unconditionally inter-subject similarity enforcement is likely to yield a suboptimal classification performance [38]. In other word, the MCI subjects are less separable from the healthy controls, based on the brain functional networks constructed using GSR. Thus, a new method that can account for both inter-subject consistency and inter-group separability is highly desired for connectome-based individual diagnosis.
So far, many previous studies about unsupervised clustering, classification or statistical difference analysis on the brain disease cohort [25, 37, 39, 40] have suggested that subjects from the same group often have larger FC similarity than those from different groups. Recently, a connectivity strength-weighted SR method was proposed for the individual brain network construction by integrating FC connectivity strength prior to better optimize brain functional network [41]. This pioneering study indicates that the network modeling with the guidance from individual FC strength could achieve more biological meaningful results and also yield improved disease classification accuracy. Inspired by these observations, we propose to explore individual FC information and introduce such a prior into the GSR-based network modeling with the goal of preserving systematical group difference without losing the merit of inter-subject consistency contributed by the group sparse learning. In particular, we first compute inter-regional pairwise FC by measuring temporal synchronization of the BOLD signals with PC for each individual, and then incorporate these PC-based FC strengths as a priori to guide the group-level brain network modeling in the GSR learning framework for both patient and healthy control groups. We hypothesize that the constructed brain functional networks can thus share similar topological structure (i.e., comparable) but still keep adequate subject-specific connectivity patterns (i.e., separable), which will thus increase disease classification accuracy. We can refer the PC-based connectivity to as low-order FC (LOFC) since it characterizes the simple pairwise temporal correlation of BOLD signals. In addition, we further propose to estimate a high-order FC (HOFC) by measuring the inter-subject LOFC-profile similarity (by comparing the LOFC pattern of each brain region between each pair of subjects) as another guidance for GSR-based network modeling. Such a guidance is introduced by constructing a graph Laplacian that penalizes those excessive “inter-subject connectivity differences” for the subjects from the same group, while retaining sufficient connectivity differences between subjects from different groups. Therefore, our method can seamlessly integrate both individual LOFC strength and inter-subject LOFC similarity (i.e., HOFC across subjects) into the same GSR-based network estimation framework, namely “Strength- and Similarity-Guided GSR (SS-GSR)”. Because the SSGSR can exploit and utilize both LOFC and HOFC priors, we expect this will provide more reliable and biologically meaningful brain functional networks that can facilitate individualized MCI diagnosis.
To validate the effectiveness of our proposed methods, we conduct an experimental study based on the rs-fMRI data from the ADNI-2 dataset. Extensive comparisons are carried out between our method and other state-of-the-art algorithms for MCI diagnosis, a challenging problem due to subtle pathological changes, compared with large inter-subject variability. Experimental results show that our methods can not only effectively detect group difference, but also significantly improve the brain functional connectomics-based MCI diagnosis.
2. Methods
2.1. General GSR-based Functional Network Construction
Suppose that contains the mean time series of a total of R regions-of-interest (ROIs) for the i-th subject, where P is the number of temporal points in each mean time series. Without loss of generality, let us assume that has been de-meaned and variance-standardized. With PC, the LOFC network of each subject i can be roughly estimated by calculating the full correlation , such that the r-th column in Ci characterizes the functional interactions between the r-th ROI and all other ROIs (i.e., one-to-all LOFC-pattern of the r-th ROI for the i-th subject). Different from PC, SR estimates such a one-to-all LOFC-pattern through linearly regressing BOLD signals from the r-th ROI by BOLD signals of all other regions using a l1-norm sparse regularization:
| (1) |
where λ is a regularization parameter controlling the sparsity of . Note that SR models a brain functional network for each subject separately, which may easily lead to relatively large inter-subject variability in . GSR-based brain functional network modeling can alleviate such a problem by jointly estimating non-zero connections across subjects via l2,1-norm regularization-based group lasso:
| (2) |
where consists of the one-to-all LOFC patterns of the r-th ROI for all N subjects, and λ controls the extent of group sparsity. The brain functional networks modeled by GSR will share similar topological structures (by enforcing similar nonzero or zero connectivities for all subjects) to reduce inter-subject variability. However, an inherent problem of GSR roots in the group Lasso constraint term, which could sacrifice the potentially important between-group differences that often benefit the disease diagnosis. Next, we describe our SSGSR model to resolve this problem.
2.2. Strength-Guided GSR (SGSR)
To improve brain disease diagnosis, we need to find out appropriate priors to guide the GSR model but will not sacrifice the important group difference in the constructed networks. We propose to incorporate the individual LOFC strength and inter-subject LOFC pattern similarity to the GSR-based network construction for providing better separability between different groups. The details of our proposed SSGSR algorithm are described below.
We first propose to incorporate the PC-based individual FC strengths into the GSR method to guide group-level brain functional network modeling. To this end, a weighting term is defined based on each subjects PC-based LOFC strength as to penalize the estimated link between the r-th and the k-th ROIs (where i denotes the i-th subject). Accordingly, a LOFC-strength-guided GSR (SGSR) model can be formulated as:
| (3) |
where is a weighting matrix with elements being , and denotes the element-wise product. That is, the link with larger LOFC strength (more likely to be the true connectivity) between these two ROIs will got less penalized while the link(s) with smaller LOFC strength (more noise-pruned) will get more penalized. In this way, these modeled brain functional networks hold the group-shared network topological structure and also reflect the subject-specific raw functional connectivity strength. In other words, this modeling method can not only ensure more biologically meaningful brain functional network construction, but also achieve improved network separability between subjects from different groups, under the hypothesis that the biologically meaningful functional networks indeed contain information for the group separation. We call this method as (PC-based FC) Strength-Guided GSR, shortly as SGSR.
2.3. Strength- and Similarity-Guided GSR (SSGSR)
It should be noted that the aforementioned SGSR model only considers the individual-level LOFCs as weights in the network construction. The major drawbacks of this method are 1) the LOFC used can only measure simple functional dependence between two brain regions, and 2) the LOFC-weighting is carried out for each individual separately, while the inter-subject similarity of LOFC is important for classification but has been ignored. To this end, we further propose to estimate a HOFC by measuring inter-subject LOFC profile similarity as an additional source of guidance for the SGSR model. In the following, we introduce the details on how the HOFC constraint can be integrated into the SGSR-based method towards better brain functional network construction.
Let and denote the regional LOFC-patterns (estimated by PC) of the r-th ROI (one-to-all LOFC) for the i-th and the j-th subjects, respectively. A graph Laplacian can be constructed with a similarity matrix with defining the pairwise similarity of subjects in terms of their LOFC patterns for the r-th ROI. Then, a similarity-preserving regularization term can be defined to incorporate inter-subject similarity/difference as follows:
| (4) |
where , and is a diagonal matrix with its diagonal elements defined as . By integrating the regularization term Ωr into (3), our newly proposed SSGSR model can be formulated as:
| (5) |
where λ1 and λ2 are the regularization parameters used to control group sparsity and inter-subject LOFC-pattern similarity, respectively. In the model formulated above, by further adding the second regularization term Ωr, we encourage inter-subject brain network resemblance if their PC-based regional LOFC patterns are similar. This will act with a power of suppressing the within-group FC differences while retaining the sufficient between-group differences, under a generally acceptable hypothesis that the overall LOFC similarity for subjects within a group is larger than subjects from different groups. In other words, the proposed new model will allow us to achieve good between-group separability without losing the merit of group sparsity. Under such situation, we can achieve the improved individual separability to further promote connectomics-based brain disease diagnosis. This enhanced separability also has its biological meaning, as suggested by numerous previous studies [25, 39] using unsupervised clustering or classification to group subjects from the same group. Therefore, we call our method as (PC-based FC) Strength- and (PC-based FC) Similarity-Guided GSR, shortly as SSGSR, which is an improved version of both GSR and SGSR. Of note, the SSGSR can be simply applied to multiple-group studies, or single-group studies that focus on inter-subject variability, because no group label is used during the functional network construction.
Fig. 1 illustrates the framework of the SSGSR algorithm for brain network modeling. Specifically, for the i-th subject, the constructed brain functional
Figure 1:
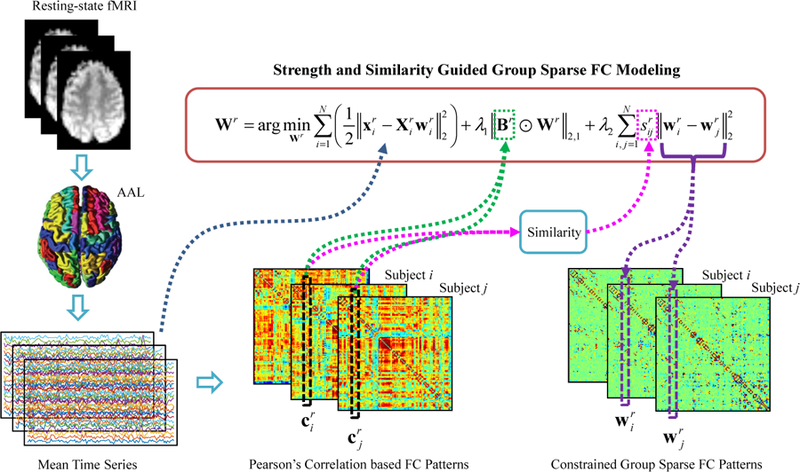
Framework of the proposed method for brain functional network construction.
network is formed as , where consists of the estimated FCs between the r-th ROI and all other ROIs. Since the network matrix Gi is typically asymmetric, a symmetry operation can be further carried out to achieve a symmetric network (although in classification study this assumption is not necessary). The optimization problems of the aforementioned network modeling methods can be solved based on the group sparse learning [42, 43]. Some other algorithms [44, 45, 46] about matrix factorization could also be adopted to solve these optimization problems.
3. Experiments
3.1. Data Acquisition and Pre-processing
In this study, we used the Alzheimers Disease Neuroimaging Initiative (ADNI) dataset (http://adni.loni.usc.edu/) for validation of our proposed functional network modeling algorithms. ADNI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and non-profit organizations. The original goal was to define biomarkers for use in clinical trials to determine the most appropriate way to measure treatment effects of AD. The current goal has been extended to discover more effective methods to early detect AD at its pre-dementia stage.
A total of 52 normal control (NC) subjects and 52 MCI patients with rs-fMRI data are selected from the ADNI-2 dataset in our experiments. Informed consent was obtained from all individual participants included in the study. Subjects from both classes are age- and gender-matched, and they were all scanned using 3.0T Philips scanners. The rs-fMRI data are preprocessed using SPM8 software (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) according to a well-accepted pipeline. Specifically, the first three volumes of each subject are discarded before preprocessing for magnetization equilibrium. Preceded by rigid-body registration for head motion correction, the rs-fMRI data are normalized to Montreal Neurological Institute (MNI) space and spatially smoothed using a Gaussian kernel with full-width-at-half-maximum (FWHM) of 6 × 6 × 6 mm3. Of note, scrubbing is not performed on the data with the frame-wise displacement (FD) larger than 0.5 mm to avoid introducing additional artifacts. However, during data screening, the subjects with more than 2.5-min rs-fMRI data and FD > 0.5 are excluded from further processing. With the Automated Anatomical Labeling (AAL) template, the rs-fMRI data are then parcellated into 116 ROIs. In each ROI, the mean BOLD time series is extracted and band-pass filtered between 0.015 and 0.15 Hz. Head motion parameters and the mean BOLD time series of both white matter and cerebrospinal fluid are regressed out for reducing the potential interference to the subsequent brain functional network construction.
3.2. Intuitive Comparison of Different Brain Functional Network Construction Methods
Fig. 2 visualizes the representative brain functional networks of four randomly selected subjects (i.e., two MCIs and two NCs) constructed using PC, SR, GSR, SGSR, and SSGSR, respectively. Compared with the other four sparse representation-based networks, PC-based networks contain much denser connections and have prominently larger individual variability. To further investigate the inter-subject variability, the standard deviation of each connection is calculated across subjects within each of MCI and NC groups, and further averaged for each of the constructed brain functional networks (see Fig. 3). We also evaluate the separability of the brain functional networks between the MCIs and the NCs by calculating the discriminability index, defined by squared pointwise biserial correlation coefficient (r2 value) [47] in Fig. 4, where the larger r2 value indicates higher separability. The number of connections with r2 > 0.05 is 122, 134, 152, 188, and 246 for PC, SR, GSR, SGSR, and SSGSR, respectively. As shown in Fig. 3, the networks derived from GSR, SGSR and SSGSR present relatively lower inter-subject variability, compared with the PC- and SR-based networks, indicating the effectiveness of the group sparsity constraint in reducing individual variability. Although the GSR achieves the best comparability, as indicated by Fig. 4, it fails to provide satisfactory separability between subjects from two different groups. Instead, by incorporating individual FC strength in the GSR, the SGSR-based brain functional networks provide an improved between-group separability. Furthermore, the SSGSR not only utilizes individual FC strength but also, more importantly, explicitly integrates the inter-subject FC pattern similarity into the GSR model, thus further improving between-group separability.
Figure 2:
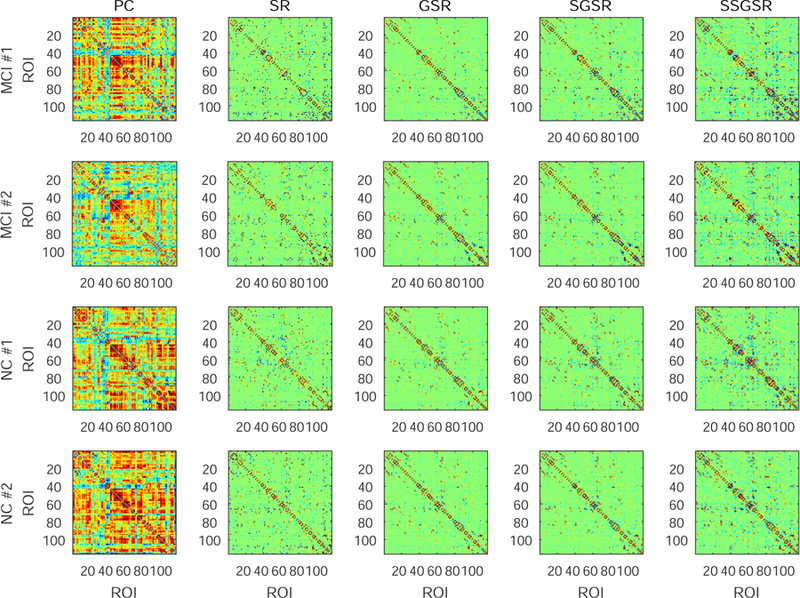
Comparison of brain functional networks of four subjects (two MCIs and two NCs), constructed by five different methods: Pearsons correlation (PC), sparse representation (SR), group sparse representation (GSR), strength guided group sparse representation (SGSR), and strength and similarity guided group sparse representation (SSGSR).
Figure 3:
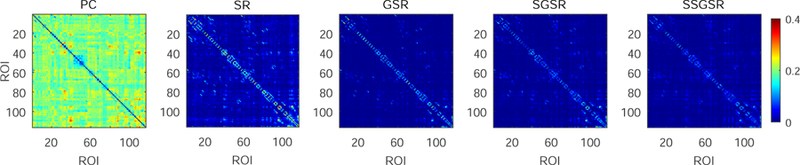
Within-group inter-subject variability of the brain functional networks constructed by PC, SR, GSR, SGSR and SSGSR, respectively. The standard deviation of each connection is calculated across subjects within each of MCI and NC groups, and then averaged to evaluate the inter-subject variability.
Figure 4:
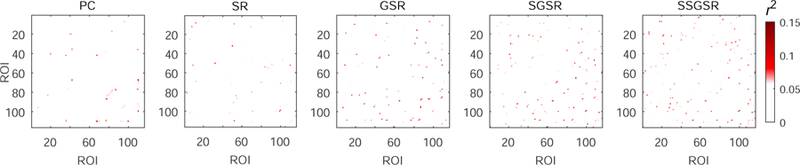
Separability of each connection in the brain functional networks constructed by PC, SR, GSR, SGSR and SSGSR, respectively. The separability is evaluated by computing the discriminability index r2 value.
3.3. MCI Classification and Performance Evaluation
For each network modeling method, a feature vector is formed by concatenating the upper triangular elements of the constructed network of each subject. That is, the dimensionality of the feature vector is 116 × (116 1)/2 = 6670. Two-sample t-tests with a significance level of p < 0.05 (uncorrected) are carried out to reduce the redundant features. Furthermore, least absolute shrinkage and selection operator (Lasso) [48, 49, 50] is adopted to select the feature subset with higher discriminability. Finally, a support vector machine (SVM) with a linear kernel is trained on the selected feature subset for MCI classification. The whole procedure is illustrated by Fig. 5.
Figure 5:
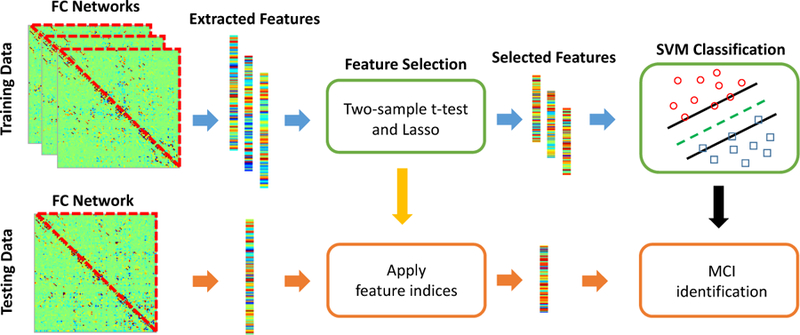
Brain functional network-based MCI classification procedure.
Classification performance is evaluated based on classification accuracy (ACC), area under ROC curve (AUC), sensitivity (SEN), and specificity (SPE). These statistical measures are defined as:
| (6) |
| (7) |
where TP, TN, FP and FN denote the true positive, true negative, false positive and false negative, respectively. Thus, ACC measures the proportion of subjects correctly classified among all subject, SEN and SPE correspond to the proportions of MCI patients and NC correctly classified, respectively. ROC curve is a graphical plot illustrating the diagnostic ability of a binary classifier system as its discrimination threshold is varied. AUC represents the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example.
To evaluate the effectiveness of our proposed framework, we have made extensive comparisons with the brain functional networks constructed by Pearson’s correlation (PC), sparse representation (SR), connectivity-weighted SR (WSR) [41], group sparse representation (GSR) [36], strength-guided GSR (SGSR), and both strength and similarity-guided (SSGSR), respectively, using the same dataset. The leave-one-out cross-validation (LOOCV) scheme is adopted for evaluation of diagnosis performance. In each fold of LOOCV procedure, an additional inner LOOCV is also carried out on the training data to determine the optimal hyper-parameters (i.e., λ for SR, WSR, GSR, and SGSR, and λ1, λ2 for SSGSR, as well as the soft-margin parameter C for SVM). The selection ranges of λ, λ1 and λ2 are [0.01, 0.02, …, 0.1], while C is selected from [0.05, 0.1, …, 1].
Fig. 6 shows the classification results derived by different brain functional network modeling methods. Compared with PC, all of other sparse representation-based methods improved the classification accuracy in the varying degrees. Among them, the proposed SSGSR method produced the highest accuracy of 88.5%, with improvements of 24.1%, 18.3%, 9.7%, 10.6% and 4.8% compared with PC, SR, WSR, GSR, and SGSR, respectively. Fig. 7 further depicts the ROC curves derived by the comparison methods. To investigate the significance of classification performance difference between different methods, we have carried out a non-parametric statistical analysis, namely DeLong’s test [51], for the comparison of each two ROC curves calculated on the dataset, with a confidence interval of 95%. The results indicate that SSGSR performs significantly better than PC, SR, WSR, GSR and SGSR with p values = 1.26 × 10−6, 3.34 × 10−6, 0.003, 0.001 and 0.028, respectively.
Figure 6:
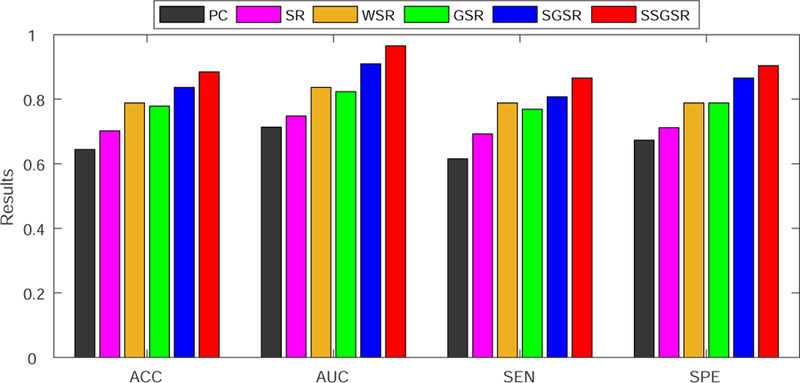
Classification performance comparison among different methods.
Figure 7:
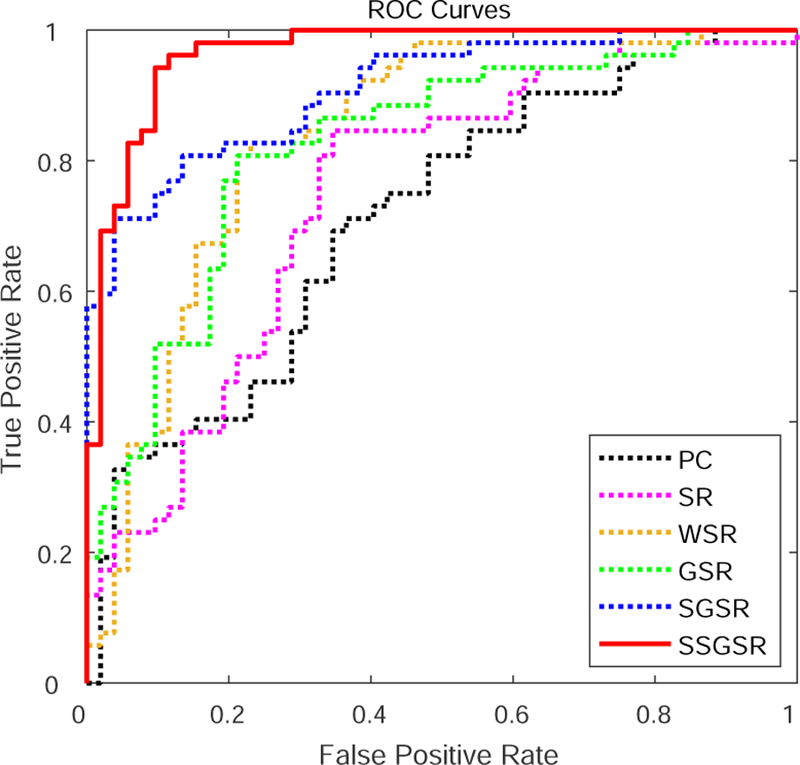
ROC curves derived by different methods for MCI classification.
4. Discussion
4.1. Performance Comparison with State-of-the-Art Results
In addition to the above-mentioned experimental analyses, we also compare the performance of our proposed SSGSR method with the performances of several recent state-of-the-art studies that also use rs-fMRI data for MCI vs. NC diagnosis (see Table 1). These state-of-the-arts are briefed as follows. Wee et al. [36] combined group Lasso model with multi-spectrum strategy to construct group-level brain networks for MCI diagnosis. Wang et al. [29] proposed to estimate the frequency-dependent brain networks using wavelet-based correlations of both high- and low-resolution parcellation units. Graph theoretical analyses were then implemented on these constructed brain networks for distinguishing MCI individuals from NC subjects. Challis et al. [52] introduced a Bayesian Gaussian process logistic regression model with covariance-based connectivity metric to MCI classification. Zhang et al. [53] constructed PC-based brain networks with two sample t-test for feature extraction, and designed an l2-regularized logistic regression classifier for MCI diagnosis. Among all these comparison methods, our approach achieved the best classification performance with higher ACC, AUC and SPE. Moreover, the experimental results derived from our study are based on the largest number of subjects among all other state-of-the-arts studies under comparison, thus providing further evidence for the reliability, generalization ability and efficacy of our proposed method.
Table 1:
Comparison with other existing studies using rs-fMRI data for MCI vs. NC classification.
It should be noted that feature selection and classification were separately implemented in our diagnosis framework. These two procedures could be integrated into one step using more advanced machine learning technologies, such as random forest [54] or deep learning [55], which may provide further improved diagnosis performance. This is worth our further investigation.
4.2. Parameter Sensitivity
The effectiveness of our proposed method is affected by the selection of hyperparameters, i.e., λ1 for strength-weighted group sparsity and λ2 for inter-subject LOFC pattern similarity. In our experiment, we implement a grid search to select the optimal parameter values on the training data using inner LOOCV. To investigate the parameter sensitivity of our network modeling method, we evaluate effects of varying values of these two hyperparameters on classification accuracy using LOOCV with all subjects. Fig. 8 depicts classification accuracies obtained using the brain networks constructed by our proposed SSGSR method with different settings for the aforementioned hyperparameters. The best accuracy of 91.4% is achieved by using λ1 = 0.04 for strength-weighted sparsity and λ2 = 0.05 for similarity constraint. It can be seen that the classification accuracy 88.5% yielded by our method with the hyperparameters estimated from the inner LOOCV is close to the best (up-limit) accuracy 91.4% that is achieved by using the specific parameters selected based on all subjects. Our future study will further validate performance of the proposed algorithm on a completely independent dataset.
Figure 8:
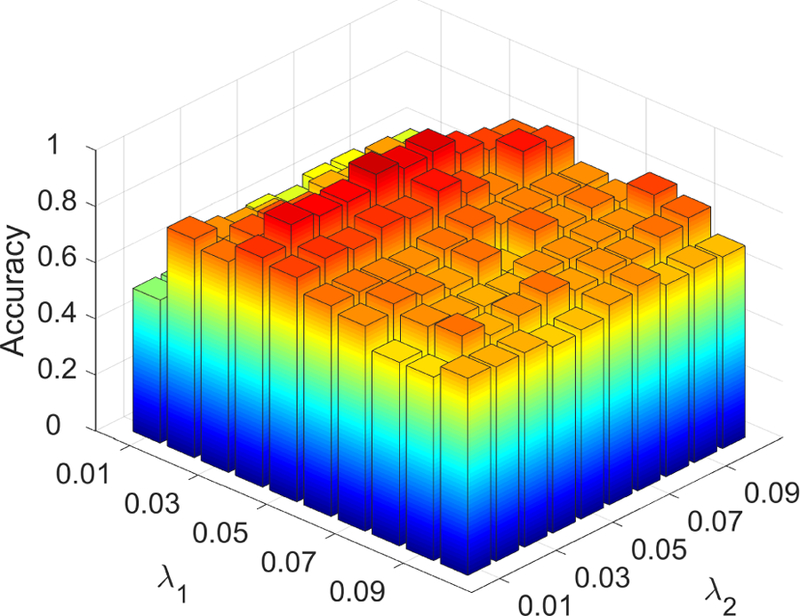
Classification accuracy derived based on the brain functional networks constructed by SSGSR with different values of the hyperparameters. The parameter range is [0.01, 0.02, … , 0.1]. The results are obtained using LOOCV on all subjects. The highest accuracy is 91.4% when λ1 = 0.04 and λ2 = 0.05.
4.3. Most Discriminative Connections and Brain Regions
To further validate our method, we investigate the connections with potential biological meaning (i.e., importance for MCI identification) based on the brain functional networks modeled by our proposed SSGSR method. These connections are regarded as potential imaging biomarkers for early AD diagnosis. Here, the values of the weighting coefficients of the trained SVM model reflect the importance of selected features for accurate MCI classification. We calculate the mean SVM-derived weighting coefficient of each feature across all the LOOCV folds during the training process, since the selected features vary in each LOOCV fold. Fig. 9 shows the top ten discriminative connections. Fig. 10 further presents the 19 brain regions involved in the top ten discriminative connections. A approach for 3D visualization of these connections and brain regions can be found in literature [56].
Figure 9:
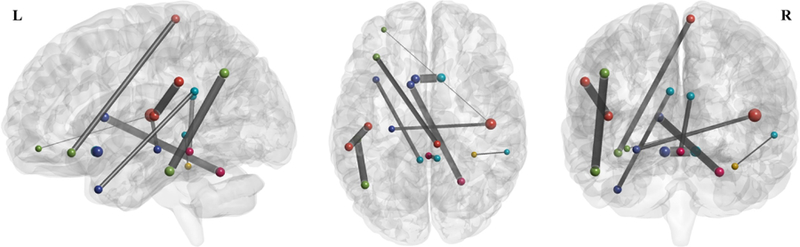
The top ten discriminative connections determined by the weighting coefficients of SVM based on the brain functional networks constructed using our proposed SSGSR method.
Figure 10:
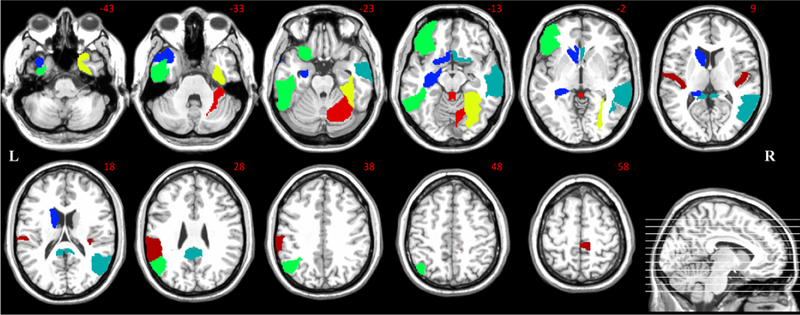
The discriminative brain regions corresponding to the top ten selected connections.
Most of these brain regions have been indicated to be closely related to AD pathology in previous studies. Specifically, many selected regions, including the hippocampus, posterior cingulate gyrus, middle temporal gyrus, angular gyrus, and supramarginal gyrus, are included or partially included in the default mode network (DMN). It is believed that the DMN plays an important role in high-level cognitive functions, including episodic memory [57], while the abnormality of the DMN functional connectivities can be observed across a range of neurological disorders, including AD and MCI [58]. Extensive researches have indicated that the hippocampus is sensitive to the pathology attack in the early stage of AD [59, 60]. Abnormal structural, functional, and metabolic changes were reported in the posterior cingulate gyrus of the MCI individuals [61, 62], which may be closely associated with the deficits in memory functions, object recognition, or evaluation of information [63]. Compared with stable MCI individuals, those who converted to AD had more atrophy on the left lateral temporal lobe, especially on the middle temporal gyrus [64], which has been reported as a significant imaging biomarker for distinguishing AD from NC subjects [65]. MCI individuals have been also found to show decreased centrality, compared with NC subjects, in the left angular gyrus [24]. In addition to being an important part of the DMN, the angular gyrus is also responsible for complex language functions, especially the language comprehension [66].
Beside the DMN, most of other selected brain regions have also shown their importance for early AD diagnosis. Both connectivity density reduction and network wiring efficiency decrease were also observed in the olfactory cortex of AD patients [67], which is associated with olfactory dysfunction, a sensitive and early behavioral marker for neurodegenerative diseases [68]. The inferior temporal gyrus have been confirmed to be affected in the prodromal stage of AD via pathological studies [69]; note that this region is a typical multimodal association area, closely related to advanced brain functions such as the verbal fluency [70]. The selected brain region at the left orbitofrontal cortex has been found to show the potential clinical correlations with the clinically well-described AD impairment such as the deteriorated motivation and value assignment [71]. In addition, both the right lobule VI of cerebellar hemisphere and the right lobule III of the vermis have also been shown to be affected in the early stage of AD [72]. The names and indices of these brain regions (corresponding to the most discriminative connections) are summarized in Table 2.
Table 2:
Brain regions corresponding to the most discriminative connections.
| ROI 1 |
ROI 2 |
||
|---|---|---|---|
| Index | Name | Index | Name |
| 9 | Left orbitofrontal cortex (middle) | 80 | Right transverse temporal gyrus |
| 21 | Left olfactory cortex | 22 | Right olfactory cortex |
| 15 | Left inferior frontal gyrus | 70 | Right paracentral lobule |
| 35 | Left posterior cingulate gyrus | 87 | Left middle temporal pole |
| 36 | Right posterior cingulate gyrus | 110 | Lobule III of vermis |
| 37 | Left hippocampus | 80 | Right transverse temporal gyrus |
| 56 | Right fusiform gyrus | 86 | Right middle temporal gyrus |
| 63 | Left supramarginal gyrus | 79 | Left transverse temporal gyrus |
| 65 | Left angular gyrus | 89 | Left inferior temporal gyrus |
| 71 | Left caudate nucleus | 100 | Right lobule VI of cerebellar hemisphere |
5. Conclusions
In this study, we propose a more accurate and biologically meaningful brain functional network modeling method, namely SSGSR, for better MCI individual identification. Our model seamlessly integrates both low- and high-level functional connectivity priors to guide the brain functional network construction, which effectively captures individual’s robust and strong connectivity strength and incorporates the advantage of inter-subject connectivity pattern (dis)similarity for better detection of group differences. Accordingly, more accurate brain functional network modeling is achieved by using our proposed SSGSR method, as shown by not only significant improvement of individualized MCI detection but also discovery of more biologically meaningful functional connectivity biomarkers. The effectiveness of our method has also been proven by comparing with multiple competing approaches on the same dataset and also with the results reported in other state-of-the-art literature. All these evidence suggest the promise of our proposed method for possible clinical studies, especially for biomarker detection and personalized brain connectomics-based disease diagnosis. Our future studies will optimize the selection strategy of model parameters in a more efficient way, and validate the performance of our method on additional independent datasets.
Acknowledgements
This study is partially supported by NIH grants (EB006733, EB008374, EB009634, MH107815, AG041721, and AG042599). Dr. S.-W. Lee was partially supported by Institute for Information & Communications Technology Promotion (IITP) grant funded by the Korea government (No. 2017–0-00451).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].A. Association, et al. , Alzheimer’s disease facts and figures, Alzheimers Dement. 9 (2) (2013) 208–245. [DOI] [PubMed] [Google Scholar]
- [2].Gauthier S., Reisberg B., Zaudig M., Petersen RC., Ritchie K., Broich K., Belleville S., Brodaty H., Bennett D., Chertkow H., et al. , Mild cognitive impairment, The Lancet 367 (9518) (2006) 1262–1270. [DOI] [PubMed] [Google Scholar]
- [3].Amlien I., Fjell A., Diffusion tensor imaging of white matter degeneration in Alzheimers disease and mild cognitive impairment, Neuroscience 276 (2014) 206–215. [DOI] [PubMed] [Google Scholar]
- [4].Cuingnet R., Gerardin E., Tessieras J., Auzias G., Lehéricy S., Habert M-O., Chupin M., Benali H., Colliot O., Initiative ADN., et al. , Automatic classification of patients with Alzheimer’s disease from structural MRI: a comparison of ten methods using the ADNI database, NeuroImage 56 (2) (2011) 766–781. [DOI] [PubMed] [Google Scholar]
- [5].Zhang D., Wang Y., Zhou L., Yuan H., Shen D., Multimodal classification of Alzheimer’s disease and mild cognitive impairment, NeuroImage 55 (3) (2011) 856–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Wang J., Wang Q., Peng J., Nie D., Zhao F., Kim M., Zhang H., Wee CY., Wang S., Shen D., Multi-task diagnosis for autism spectrum disorders using multi-modality features: A multi-center study, Hum. Brain Mapp. 38 (6) (2017) 3081–3097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zhu X., Suk H-I., Lee S-W., Shen D., Subspace regularized sparse multitask learning for multiclass neurodegenerative disease identification, IEEE Trans. Biomed. Eng. 63 (3) (2016) 607–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Liu X., Zhou L., Wang L., Zhang J., Yin J., Shen D., An efficient radius-incorporated MKL algorithm for alzheimer s disease prediction, Pattern Recogn. 48 (7) (2015) 2141–2150. [Google Scholar]
- [9].Zu C., Wang Z., Zhang D., Liang P., Shi Y., Shen D., Wu G., Robust multi-atlas label propagation by deep sparse representation, Pattern Recogn. 63 (2017) 511–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Zhu X., Suk H-I., Wang L., Lee S-W., Shen D., A novel relational regularization feature selection method for joint regression and classification in ad diagnosis, Med. Image Anal. 38 (2017) 205–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Cao P., Shan X., Zhao D., Huang M., Zaiane O., Sparse shared structure based multi-task learning for mri based cognitive performance prediction of Alzheimers disease, Pattern Recogn. 72 (2017) 219–235. [Google Scholar]
- [12].Tong T., Gray K., Gao Q., Chen L., Rueckert D., Initiative ADN., et al. , Multi-modal classification of Alzheimer’s disease using nonlinear graph fusion, Pattern Recogn. 63 (2017) 171–181. [Google Scholar]
- [13].Fox MD., Greicius M., Clinical applications of resting state functional connectivity, Front. Syst. Neurosci. 4 (2010) 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Smith SM., Beckmann CF., Andersson J., Auerbach EJ., Bijster-bosch J., Douaud G., Duff E., Feinberg DA., Griffanti L., Harms MP., et al. , Resting-state fMRI in the human connectome project, NeuroImage 80 (2013) 144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Bullmore E., Sporns O., Complex brain networks: graph theoretical analysis of structural and functional systems, Nat. Rev. Neurosci. 10 (3) (2009) 186–198. [DOI] [PubMed] [Google Scholar]
- [16].Sporns O., The human connectome: a complex network, Ann N Y Acad Sci. 1224 (1) (2011) 109–125. [DOI] [PubMed] [Google Scholar]
- [17].Rubinov M., Sporns O., Complex network measures of brain connectivity: uses and interpretations, NeuroImage 52 (3) (2010) 1059–1069. [DOI] [PubMed] [Google Scholar]
- [18].Stam C., Jones B., Nolte G., Breakspear M., Scheltens P., Small-world networks and functional connectivity in Alzheimer’s disease, Cereb. Cortex 17 (1) (2006) 92–99. [DOI] [PubMed] [Google Scholar]
- [19].Stam C., De Haan W., Daffertshofer A., Jones B., Manshanden I., Van Cappellen Van Walsum A., Montez T., Verbunt J., De Munck J., Van Dijk B., et al. , Graph theoretical analysis of magnetoencephalographic functional connectivity in alzheimer’s disease, Brain 132 (1) (2008) 213–224. [DOI] [PubMed] [Google Scholar]
- [20].Lynall M-E., Bassett DS., Kerwin R., McKenna PJ., Kitzbichler M., Muller U., Bullmore E., Functional connectivity and brain networks in schizophrenia, J. Neurosci. 30 (28) (2010) 9477–9487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Assaf M., Jagannathan K., Calhoun VD., Miller L., Stevens MC., Sahl R., O’boyle JG., Schultz RT., Pearlson GD., Abnormal functional connectivity of default mode sub-networks in autism spectrum disorder patients, NeuroImage 53 (1) (2010) 247–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Yao Z., Zhang Y., Lin L., Zhou Y., Xu C., Jiang T., Initiative ADN., et al. , Abnormal cortical networks in mild cognitive impairment and Alzheimer’s disease, PLoS Comput. Biol. 6 (11) (2010) e1001006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Sheline YI., Raichle ME., Resting state functional connectivity in preclinical Alzheimers disease, Biol. Psychiat. 74 (5) (2013) 340–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Liu Z., Zhang Y., Yan H., Bai L., Dai R., Wei W., Zhong C., Xue T., Wang H., Feng Y., et al. , Altered topological patterns of brain networks in mild cognitive impairment and Alzheimer’s disease: a resting-state fMRI study, Psychiat. Res. Neuroim. 202 (2) (2012) 118–125. [DOI] [PubMed] [Google Scholar]
- [25].Shen H., Wang L., Liu Y., Hu D., Discriminative analysis of resting-state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI, NeuroImage 49 (4) (2010) 3110–3121. [DOI] [PubMed] [Google Scholar]
- [26].Zhang Y., Zhang H., Chen X., Lee S-W., Shen D., Hybrid high-order functional connectivity networks using resting-state functional mri for mild cognitive impairment diagnosis, Sci. Rep. 7 (1) (2017) 6530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chen X., Zhang H., Gao Y., Wee C-Y., Li G., Shen D., High-order resting-state functional connectivity network for mci classification, Hum. Brain Mapp. 37 (9) (2016) 3282–3296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Sanz-Arigita EJ., Schoonheim MM., Damoiseaux JS., Rombouts SA., Maris E., Barkhof F., Scheltens P., Stam CJ., Loss of ‘small-world’networks in alzheimer’s disease: graph analysis of FMRI resting-state functional connectivity, PloS One 5 (11) (2010) e13788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Wang J., Zuo X., Dai Z., Xia M., Zhao Z., Zhao X., Jia J., Han Y., He Y., Disrupted functional brain connectome in individuals at risk for Alzheimer’s disease, Biol. Psychiat. 73 (5) (2013) 472–481. [DOI] [PubMed] [Google Scholar]
- [30].Brier MR., Thomas JB., Fagan AM., Hassenstab J., Holtzman DM., Benzinger TL., Morris JC., Ances BM., Functional connectivity and graph theory in preclinical Alzheimer’s disease, Neurobiol. Aging. 35 (4) (2014) 757–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Lee H., Lee DS., Kang H., Kim B-N., Chung MK., Sparse brain network recovery under compressed sensing, IEEE Trans. Med. Imag. 30 (5) (2011) 1154–1165. [DOI] [PubMed] [Google Scholar]
- [32].Zhang Y., Zhou G., Jin J., Zhao Q., Wang X., Cichocki A., Sparse Bayesian classification of eeg for brain–computer interface, IEEE Trans. Neural Networks Learn. Syst. 27 (11) (2016) 2256–2267. [DOI] [PubMed] [Google Scholar]
- [33].Jin Z., Zhou G., Gao D., Zhang Y., EEG classification using sparse bayesian extreme learning machine for brain–computer interface, Neural Comput. Appl. (2018) 1–9 10.1007/s00521-018-3735-3. [DOI]
- [34].Huang S., Li J., Sun L., Ye J., Fleisher A., Wu T., Chen K., Reiman E., Initiative ADN., et al. , Learning brain connectivity of Alzheimer’s disease by sparse inverse covariance estimation, NeuroImage 50 (3) (2010) 935–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Zhang J., Zhou L., Wang L., Subject-adaptive integration of multiple sice brain networks with different sparsity, Pattern Recogn. 63 (2017) 642–652. [Google Scholar]
- [36].Wee C-Y., Yap P-T., Zhang D., Wang L., Shen D., Group-constrained sparse fMRI connectivity modeling for mild cognitive impairment identification, Brain Struct. Funct. 219 (2) (2014) 641–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Varoquaux G., Gramfort A., Poline J-B., Thirion B., Brain covariance selection: better individual functional connectivity models using population prior, in: Advances in Neural Information Processing Systems, 2010, pp. 2334–2342.
- [38].Suk H-I., Wee C-Y., Lee S-W., Shen D., Supervised discriminative group sparse representation for mild cognitive impairment diagnosis, Neuroinformatics 13 (3) (2015) 277–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Zeng L-L., Shen H., Liu L., Hu D., Unsupervised classification of major depression using functional connectivity MRI, Hum. Brain Mapp. 35 (4) (2014) 1630–1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Koch W., Teipel S., Mueller S., Benninghoff J., Wagner M., Bokde AL., Hampel H., Coates U., Reiser M., Meindl T., Diagnostic power of default mode network resting state fMRI in the detection of Alzheimer’s disease, Neurobiol. Aging. 33 (3) (2012) 466–478. [DOI] [PubMed] [Google Scholar]
- [41].Yu R., Zhang H., An L., Chen X., Wei Z., Shen D., Connectivity strength-weighted sparse group representation-based brain network construction for MCI classification, Hum. Brain Mapp. 38 (5) (2017) 2370–2383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Liu J., Ji S., Ye J., Multi-task feature learning via efficient l2,1-norm minimization, in: In: Proceedings of the Twenty-fifth Conference on Uncertainty in Artificial Intelligence, AUAI Press, 2009, pp. 339–348. [Google Scholar]
- [43].Zhang Y., Nam CS., Zhou G., Jin J., Wang X., Cichocki A., Temporally constrained sparse group spatial patterns for motor imagery bci, IEEE Trans. Cybern. (99) (2018) 1–11. doi: 10.1109/TCYB.2018.2841847. [DOI] [PubMed] [Google Scholar]
- [44].Lee DD., Seung HS., Algorithms for non-negative matrix factorization, in: In: Advances In Neural Information Processing Systems (NIPS 2001), 2001, pp. 556–562. [Google Scholar]
- [45].Song D., Meyer DA., Min MR., Fast nonnegative matrix factorization with rank-one admm, in: In: NIPS 2014 Workshop on Optimization for Machine Learning (OPT2014), 2014. [Google Scholar]
- [46].Zhang Y., Zhou G., Zhao Q., Cichocki A., Wang X., Fast nonnegative tensor factorization based on accelerated proximal gradient and low-rank approximation, Neurocomputing 198 (2016) 148–154. [Google Scholar]
- [47].Zhang Y., Zhou G., Zhao Q., Jin J., Wang X., Cichocki A., Spatial-temporal discriminant analysis for ERP-based brain-computer interface, IEEE Trans. Neural Syst. Rehabil. Eng. 21 (2) (2013) 233–243. [DOI] [PubMed] [Google Scholar]
- [48].Tibshirani R., Regression shrinkage and selection via the lasso, J. R. Stat. Soc. Series B Stat. Methodol. (1996) 267–288.
- [49].Zhang Y., Zhou G., Jin J., Wang X., Cichocki A., Optimizing spatial patterns with sparse filter bands for motor-imagery based brain-computer interface, J. Neurosci. Meth. 255 (2015) 85–91. [DOI] [PubMed] [Google Scholar]
- [50].Zhang Y., Zhou G., Jin J., Zhao Q., Wang X., Cichocki A., Aggregation of sparse linear discriminant analyses for event-related potential classification in brain-computer interface, Int. J. Neural Syst. 24 (1) (2014) 1450003. [DOI] [PubMed] [Google Scholar]
- [51].DeLong ER., DeLong DM., Clarke-Pearson DL., Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach, Biometrics (1988) 837–845. [PubMed]
- [52].Challis E., Hurley P., Serra L., Bozzali M., Oliver S., Cercignani M., Gaussian process classification of alzheimer’s disease and mild cognitive impairment from resting-state fMRI, NeuroImage 112 (2015) 232–243. [DOI] [PubMed] [Google Scholar]
- [53].Zhang X., Hu B., Ma X., Xu L., Resting-state whole-brain functional connectivity networks for mci classification using l2-regularized logistic regression, IEEE Trans. Nanobiosci. 14 (2) (2015) 237–247. [DOI] [PubMed] [Google Scholar]
- [54].Ni D., Ji X., Wu M., Wang W., Deng X., Hu Z., Wang T., Shen D., Cheng J-Z., Wang H., Automatic cystocele severity grading in transperineal ultrasound by random forest regression, Pattern Recogn. 63 (2017) 551–560. [Google Scholar]
- [55].LeCun Y., Bengio Y., Hinton G., Deep learning, Nature 521 (7553) (2015) 436. [DOI] [PubMed] [Google Scholar]
- [56].Chen Y., McElvain L., Tolpygo A., Ferrante D., Karten H., Mitra P., Kleinfeld D., Freund Y., The active atlas: Combining 3d anatomical models with texture detectors, in: In: International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2017), Springer, 2017, pp. 3–11. [Google Scholar]
- [57].Mevel K., Chételat G., Eustache F., Desgranges B., The default mode network in healthy aging and Alzheimer’s disease, Int. J. Alzheimers Dis. 2011. [DOI] [PMC free article] [PubMed]
- [58].Buckner RL., Andrews-Hanna JR., Schacter DL., The brain’s default network, Ann. N. Y. Acad. Sci. 1124 (1) (2008) 1–38. [DOI] [PubMed] [Google Scholar]
- [59].Wang L., Zang Y., He Y., Liang M., Zhang X., Tian L., Wu T., Jiang T., Li K., Changes in hippocampal connectivity in the early stages of alzheimer’s disease: evidence from resting state fmri, NeuroImage 31 (2) (2006) 496–504. [DOI] [PubMed] [Google Scholar]
- [60].Rombouts SA., Barkhof F., Goekoop R., Stam CJ., Scheltens P., Altered resting state networks in mild cognitive impairment and mild alzheimer’s disease: an fmri study, Hum. Brain Mapp. 26 (4) (2005) 231–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Jacobs H., Van Boxtel M., Heinecke A., Gronenschild E., Backes W., Ramakers I., Jolles J., Verhey F., Functional integration of parietal lobe activity in early alzheimer disease, Neurology 78 (5) (2012) 352–360. [DOI] [PubMed] [Google Scholar]
- [62].Buckner RL., Snyder AZ., Shannon BJ., LaRossa G., Sachs R., Fotenos AF., Sheline YI., Klunk WE., Mathis CA., Morris JC., et al. , Molecular, structural, and functional characterization of alzheimer’s disease: evidence for a relationship between default activity, amyloid, and memory, J. Neurosci. 25 (34) (2005) 7709–7717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Ries ML., Schmitz TW., Kawahara TN., Torgerson BM., Trivedi MA., Johnson SC., Task-dependent posterior cingulate activation in mild cognitive impairment, NeuroImage 29 (2) (2006) 485–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Karas G., Sluimer J., Goekoop R., Van Der Flier W., Rombouts S., Vrenken H., Scheltens P., Fox N., Barkhof F., Amnestic mild cognitive impairment: structural mr imaging findings predictive of conversion to alzheimer disease, Am. J. Neuroradiol. 29 (5) (2008) 944–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Magnin B., Mesrob L., Kinkingnéhun S., Pélégrini-Issac M., Colliot O., Sarazin M., Dubois B., Lehéricy S., Benali H., Support vector machine-based classification of alzheimers disease from whole-brain anatomical mri, Neuroradiology 51 (2) (2009) 73–83. [DOI] [PubMed] [Google Scholar]
- [66].Ni H., Zhou L., Ning X., Wang L., Exploring multifractal-based features for mild Alzheimer’s disease classification, Magn. Reson. Imaging. 76 (1) (2016) 259–269. [DOI] [PubMed] [Google Scholar]
- [67].Li Y., Wang Y., Wu G., Shi F., Zhou L., Lin W., Shen D., Initiative ADN., et al. , Discriminant analysis of longitudinal cortical thickness changes in Alzheimer’s disease using dynamic and network features, Neurobiol. Aging. 33 (2) (2012) 427–e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Frisoni GB., Prestia A., Rasser PE., Bonetti M., Thompson PM., In vivo mapping of incremental cortical atrophy from incipient to overt Alzheimers disease, J. Neurol. 256 (6) (2009) 916. [DOI] [PubMed] [Google Scholar]
- [69].Braak H., Alafuzoff I., Arzberger T., Kretzschmar H., Del Tredici K., Staging of alzheimer disease-associated neurofibrillary pathology using paraffin sections and immunocytochemistry, Acta Neuropathol. 112 (4) (2006) 389–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Scheff SW., Price DA., Schmitt FA., Scheff MA., Mufson EJ., Synaptic loss in the inferior temporal gyrus in mild cognitive impairment and alzheimer’s disease, J. Alzheimers Dis. 24 (3) (2011) 547–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Filippini N., Rao A., Wetten S., Gibson RA., Borrie M., Guzman D., Kertesz A., Loy-English I., Williams J., Nichols T., et al. , Anatomically-distinct genetic associations of APOE 4 allele load with regional cortical atrophy in alzheimer’s disease, NeuroImage 44 (3) (2009) 724–728. [DOI] [PubMed] [Google Scholar]
- [72].Wee C-Y., Yang S., Yap P-T., Shen D., Initiative ADN., et al. , Sparse temporally dynamic resting-state functional connectivity networks for early MCI identification, Brain Imaging Behav. 10 (2) (2016) 342–356. [DOI] [PMC free article] [PubMed] [Google Scholar]


