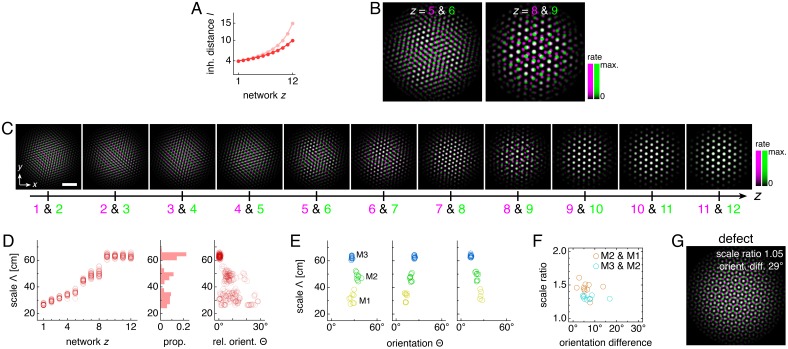
Figure 6. Discommensurate lattice relationships can produce realistic modules.

(A) We use a shallower inhibition distance profile l(z) (dark) compared to Figure 1C (light). (B) Large activity overlays from a representative simulation that emphasize discommensurate lattice relationships. (C) All activity overlays from the representative simulation in B between adjacent networks z in magenta and green, so white indicates activity in both networks. Scale bar, 50 neurons. (D–F) Data from 10 replicate simulations. (D) Left: spatial grid scales Λ(z). For each network, there are up to 30 red circles corresponding to three neurons recorded during each simulation. Middle: histogram for Λ collected across all networks. Right: spatial orientations Θ relative to the grid cell in the same simulation with largest scale. (E) Clustering of spatial scales and orientations for three representative simulations. Due to sixfold lattice symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules. (F) Spatial scale ratios and orientation differences between adjacent modules. (G) Representative activity overlay demonstrating defect with low activity overlap. Maximum inhibition distance l_max = 10, coupling spread d = 12. We use larger network size n × n = 230 × 230 to allow for discommensurate relationships whose periodicities span longer distances on the neural sheets. Other parameter values are in Table 1.

Figure 6—figure supplement 1. Representative network activities and single neuron rate maps; module clustering for all replicate simulations.

(A) Representative network activities and single neuron rate maps for the discommensurate system. Top row: network activities at the end of the simulation. Second row: activity overlays between adjacent networks depicted in the top row. In each panel, the network at smaller (larger) z is depicted in magenta (green), so white indicates regions of activity in both networks. Third row: spatial rate map of a single neuron for each z superimposed on the animal’s trajectory. Bottom row: spatial autocorrelations of the rate maps depicted in the third row. White scale bars, 50 neurons. Black scale bars, 50 cm. (B) Clustering of spatial scales and orientations for all replicate simulations. Due to sixfold lattice symmetry, orientation is a periodic variable modulo 60°. Different colors indicate separate modules.

Figure 6—figure supplement 2. Sample comparison of field-to-field firing rate variability between an experimental recording and our model.

(A) Sample experimentally recorded single neuron rate map adapted from Figure 1a of Dunn et al. (2017). (B) Sample single neuron rate map from a simulation with the same parameters as in Figure 6 that exhibits discommensurate lattice relationships. Note that firing rate decreases across fields from the bottom left to the top right of both A and B; the presence of firing rate modulation over long distances has been considered by Stemmler and Herz (2017). In B, the fields at the top right correspond to a discommensuration on the neural sheet and the fields at the bottom left correspond to a region in between discommensurations that exhibits activity overlap. A comprehensive test requires analysis with experiments using circular enclosures to eliminate confounding boundary effects (see Discussion).