Peripheral Nerve Stimulation Limits of a High Amplitude and Slew Rate Magnetic Field Gradient Coil for Neuroimaging

Abstract

Purpose:

To establish peripheral nerve stimulation (PNS) thresholds for an ultra-high performance magnetic field gradient sub-system (simultaneous 200 mT/m gradient amplitude and 500 T/m/s gradient slew rate; 1-MVA per-axis: referred to as MAGNUS) designed for neuroimaging with asymmetric transverse gradients and 42-cm inner diameter, and to determine PNS threshold dependencies on gender, age, patient positioning within the gradient sub-system, and anatomical landmarks.

Methods:

The MAGNUS head-gradient was installed in a whole-body 3.0T scanner with a custom 16-rung bird-cage transmit/receive radiofrequency coil compatible with phased-array receiver brain coils. Twenty adult subjects (10 male, mean±s.d. age=40.4±11.1 years) underwent the imaging and PNS study. The tests were repeated by displacing subject positions by 2–4 cm in the superior-inferior and anterior-posterior directions.

Results:

The X-axis (left-right) yielded mostly facial stimulation, with mean ΔG_min=111±6 mT/m, chronaxie=766±76 μsec. The Z-axis (superior-inferior) yielded mostly chest/shoulder stimulation (123±7 mT/m, 620±62 μsec). Y-axis (anterior-posterior) stimulation was negligible. X- and Z-axes thresholds tended to increase with age, and there was negligible dependency with gender. Translation in the inferior and posterior directions tended to increase X- and Z-axes thresholds, respectively. Electric field simulations showed good agreement with the PNS results. Imaging at MAGNUS gradient performance with increased PNS threshold provided a 35% reduction in noise-to-diffusion contrast as compared to whole-body performance (80 mT/m gradient amplitude, 200 T/m/sec gradient slew rate).

Conclusion:

The PNS threshold of MAGNUS is significantly higher than that for whole-body gradients, which allows for diffusion gradients with short rise-times (under 1 msec), important for interrogating brain microstructure length-scales.

INTRODUCTION

Throughout the history of MRI, generations of commercially-available and research MRI systems have strived for improvements in peak magnetic field gradient performance, specifically peak gradient amplitude (G_max) and peak slew rate (SR). The motivation for increasing SR was to shorten readout times, such as for echo planar imaging (EPI) (1) and spirals (2), which maximize waveform efficiencies and minimize time within which undesirable relaxation and susceptibility effects will accumulate. Higher G_max, on the other hand, was primarily motivated by applications requiring high amplitude gradient waveforms, such as diffusion imaging. In recent years, the demand for high gradient performance has been particularly urgent in brain MRI, especially in applications related to brain connectivity and microstructure imaging, where research MRI systems with G_max as high as 300 mT/m (3) or SR of 1200 T/m/sec (4) have been utilized for in vivo human brain imaging. However, both high SR and high G_max have not been simultaneously achieved, which benefit the fast switching EPI readouts of functional MRI and that of diffusion-weighted EPI used in measuring brain connectivity and microstructure imaging. In essence, faster SR translates to shorter echo spacings in EPI, which reduce image distortion and provide shorter echo times (5); shorter echo times lead to higher signal in short T₂ species. Higher G_max not only provides shorter diffusion waveforms that lead to reduced echo time, but also improves the image quality and sensitivity to shorter axonal length scales in microstructure imaging (6,7).

An effective way to provide both high amplitude and SR for brain imaging is to utilize head-sized gradient systems (1,4,6–9). As compared to whole-body gradients in commercially-available MRI systems, head-gradients have higher coil gain (gradient amplitude per unit current) and lower inductance (6), i.e. enabling higher G_max and SR for the same current and voltage respectively. Consequently, head-gradients may have reduced AC and DC resistances that result in less heating losses, and also improved thermal management. Head-gradients also have a smaller linear imaging field-of-view (FOV) (7), which provides the opportunity to reduce electric fields and to raise the peripheral nerve stimulation (PNS) threshold for in vivo human imaging (9,10). The higher PNS thresholds of head-gradients facilitates better gradient performance for improved human neuroimaging (5).

PNS in MRI results from rapidly-switching and high amplitude gradient waveforms (11), which cause temporally-varying magnetic gradient fields. The vector potential component of the magnetic fields cause electric fields that induce current flow in the human body (12,13). These induced electric currents in the nervous system result in perceived sensation of the stimulation. Painful or uncomfortable PNS is a well-recognized safety issue (14,15). At present, MRI gradients are generally recognized to not induce cardiac stimulation. The United States FDA guidelines recommend PNS studies with 11 or more subjects to be conducted when dB/dt exceeds 20 T/s, to establish thresholds for mild and painful stimuli (16). While these regulatory safety guidelines apply in general to all MRI gradient systems, the need for PNS studies is especially important for MRI systems capable of higher gradient amplitude and slew rates. More recently, attempts to include human body and nerve models have been utilized by electromagnetic field simulations to estimate PNS thresholds (17–19). When compared to PNS experiments, these simulations provided good agreement with the location, magnitude and orientation in whole-body and head-gradients (19), and can be a powerful way to validate PNS studies and to improve gradient designs. They also confirm higher electric field (E-field) amplitudes with whole-body gradients (primarily in the torso regions) than with head-gradients (in head and upper torso regions). However, it remains difficult to account for population variance in simulation, and it may be too computationally-expensive to perform simulations at very high spatial resolution (<1 mm) that are required for accurate depiction of nerve bundles.

In comparison to the compact 3T (C3T) head-gradient coil (9,20) that has a maximum gradient amplitude of 80 mT/m and 700 T/m/sec slew rate, the newly-designed Microstructure Anatomy Gradient for Neuroimaging with Ultrafast Scanning (MAGNUS) gradient coil can simultaneously achieve a 200 mT/m gradient amplitude and a 500 T/m/sec gradient slew rate with the same 1-MVA gradient driver (620 A and 1500 V), while maintaining a 42-cm inner diameter (ID). While MAGNUS was designed to have the same linearity (18% maximum uncorrected deviation from linearity) and 26-cm field-of-view as the C3T gradient coil, MAGNUS has a larger outer diameter of 89 cm. To first-order, the PNS characteristics of MAGNUS are expected to be similar to the C3T (9), which had significantly higher ΔG_min and SR_min than whole-body systems and were most sensitive in the X (left-right)-axis; it was also shown with a head-rotation experiment that the PNS sensitivity was dependent on anatomy rather than on the gradient coil. Another head-gradient of different design was also most sensitive in the X-axis (19). One rationale for this is the head in a supine position has a larger conductive area normal to the sagittal plane as compared to the coronal plane, that results in larger loops and increased induced E-field. This rationale and generalization of X-axis sensitivity may however not be valid, as another head-gradient design with a symmetric folded coil showed higher Y(anterior-posterior)-axis sensitivity than the X-axis instead (21). In addition, the PNS study of the C3T was amplitude-limited because the PNS threshold was either very close to (X-axis) or beyond (Y- and Z-axes) the peak hardware performance of the gradient. With a 2.5x-higher gradient amplitude, MAGNUS has both high G_max and SR that would result in even larger and more rapidly-switching waveforms. Such waveforms will be important for brain microstructure imaging, because the relevant diffusion times for axonal diameters in the brain are <1 msec. To date, axonal diameter mapping methods in human brain in vivo are limited by the gradient performance of whole-body MRI systems (<80–100 mT/m) and also by whole-body PNS (<200 T/m/sec) that produce long diffusion-encoding pulse widths (~10 msec), which consequently result in an over-estimation of axonal diameters (22).

The goal of this work is to establish PNS thresholds for the newly-designed MAGNUS head-gradient, that is able to provide very short rise-times (400 μsec) at peak amplitude (200 mT/m). In order to maximize the performance of MAGNUS it would be crucial to explore the demographic and positional dependencies of PNS, which could provide ways for optimizing stimulation thresholds. To determine PNS thresholds, in vivo human subject studies would be needed, and should be supported by E-field simulations. These PNS operating limits would be tested by high spatial resolution and high amplitude diffusion imaging on the MAGNUS system to demonstrate shorter echo times and EPI echo-spacings.

METHODS

MAGNUS gradient design and installation

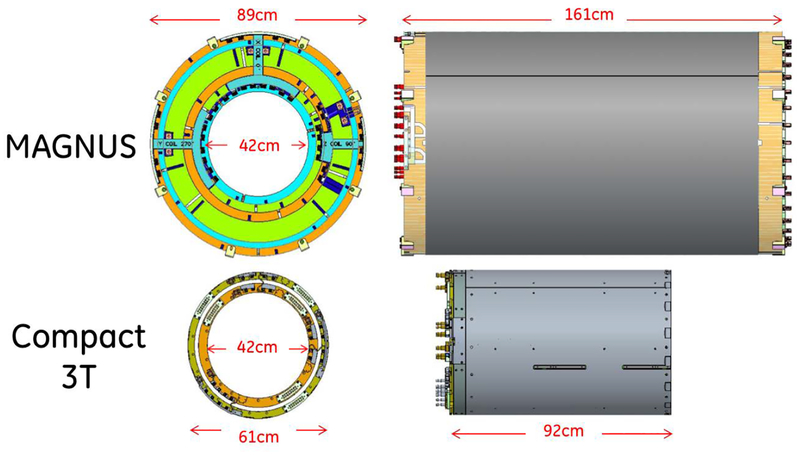
To increase its coil gain, the MAGNUS coil utilizes two design features that distinguish it from its C3T gradient coil predecessor (9). The first feature is an increased mean primary-shield coil radial separation of 18.6-cm, as compared to the 9.0-cm separation for the C3T. MAGNUS is designed for insertion in a conventional 90-cm warm bore whole-body 3T magnet, unlike that of the smaller 62-cm warm bore investigational low-cryogen C3T magnet. This increased primary-shield coil separation increases the efficiency and gain of the gradient coil (23) resulting in an approximately 30% increase in G_max for the same applied driver current. The second feature is a double-layer primary coil design, which allows the current density to be substantially increased while maintaining the physical turn density for the wire paths to within a manufacturable range. As shown in Fig.1, the gradient coil’s 42-cm ID maintains compatibility with RF coils and patient-handling similar to that of the C3T system. Like the C3T gradient coil, the MAGNUS head-gradient coil has asymmetric transverse X- and Y-gradients (24), and a symmetric Z-gradient that are of all-hollow conductor construction to allow dissipation of >50 kW of heat. It is also force- and torque-balanced (<0.30 kN and <0.26 kNm, respectively), and has low DC resistance (<0.075 Ω) and inductance (<0.92 mH).

Figure 1.

Drawings and dimensions of the MAGNUS gradient coil compared with the Compact 3T (C3T) gradient coil.

With the combined design features, the target G_max of 200 mT/m can be reached with a 620 A gradient driver. MAGNUS achieves a gradient coil gain of almost three times that of the C3T gradient (0.323 mT/m/A compared to 0.129 mT/m/A), and almost four times that of conventional whole-body MR scanners (0.05–0.08 mT/m/A). The main magnetic fields and free-space E-fields for all gradient axes are provided in Fig.S1.

Electric field modeling

PNS results from the electrical field (E-field) $\overrightarrow{E}$ induced from the rapidly changing magnetic fields of gradient coils (13), which in turn is determined by:

$$\overrightarrow{E}=-\frac{\partial \overrightarrow{A}}{\partial t}-\nabla \text{Φ}$$ (1)

where $\overrightarrow{A}$ is the vector potential caused by the current in the gradient coil and Φ is the scalar potential in the human body (17). $\overrightarrow{A}$ can be simply derived with Biot-Savart’s law for an assumed coil current I, wire geometry l, and position vector $\overrightarrow{r}$:

$$\overrightarrow{A}(\overrightarrow{r})=\frac{{\mu }_0}{2\pi }\underset{l}{\overset{}{\int }}\frac{I(\overrightarrow{r}\prime )}{\left|\overrightarrow{r}-\overrightarrow{r}\prime \right|}d\overrightarrow{l}\left({\overrightarrow{r}}^{\prime }\right).$$ (2)

Under quasi-static conditions for finite-element simulations (25,26) the scalar potential Φ, satisfies both $\nabla \cdot (\sigma \nabla \text{Φ})=-\nabla \cdot (\sigma \partial \overrightarrow{A}/\partial t)$ (due to the zero divergence condition, i.e. $\nabla \cdot \sigma \overrightarrow{E}=0$) and $\frac{d\text{Φ}}{dn}=-\widehat{n}\cdot \partial \overrightarrow{A}/\partial t$ (due to the zero normal current boundary condition, i.e. $\widehat{n}\cdot \sigma \overrightarrow{E}=0$), where σ is the electrical conductivity and $\widehat{n}$ is the unit vector perpendicular to the surface of conductive bodies.

The vector potential $\overrightarrow{A}$ map was first generated in Matlab (Mathworks, Natick, MA, USA) with a current corresponding to 10 mT/m gradient amplitude using the known wire pattern for two gradient coils – C3T (9,20) and MAGNUS. The vector potential maps were then imported into the simulation software (Sim4Life, Zurich Med Tech, Zurich, Switzerland) for computation of the E-field inside the human body (‘Duke’ human body model, IT’IS Foundation, Zurich, Switzerland). Calculations were performed using the software’s quasi-static solver at 1kHz, which corresponded to a slew rate of 62.8 T/m/sec; these were subsequently scaled to 100 T/m/sec. A mesh size of 1 mm-isotropic was used. The glabella of the human body model was first aligned to a position 2-cm inferior to the isocenter of the coil. For MAGNUS, simulations at positions 2–4 cm inferior to the initial position were also performed, corresponding to the experimental procedure. E-field maps for free space (proportional to $\overrightarrow{A}$), σ and the human-body model $\overrightarrow{E}$ are provided in Fig.S2.

Imaging and subject set-up

Twenty adult human subjects (10 males, mean age ± s.d., age = 40.8 ± 10.3 years; 10 females, age = 39.9 ± 11.3 years) were recruited in accordance with an approved institutional review board protocol for MRI and investigation of PNS thresholds. In addition to PNS tests (described below), each subject was imaged with MAGNUS inserted in an 3.0T MR Scanner (Signa MR750, GE Healthcare, Chicago, IL, USA) with its whole-body gradient and RF coil removed. No PNS tests were performed on the C3T system. A custom 37-cm ID RF transmit/receiver coil was used for transmit with an eight-channel phased-array brain coil receiver. Sagittal 3D T₁-weighted inversion recovery-prepared gradient recalled echo (TR/TE/TI=6.4/2.7/450 msec, FOV=28 cm, 2 mm-isotropic, receiver bandwidth=±31.25 kHz) was performed at the first “fixed” position and at each “displaced” position. 3D gradient linearity correction (gradwarp) was performed, utilizing 10^th-order spherical harmonics to provide the higher spatial accuracy needed in a head-gradient with smaller linear field-of-view (27).

Peripheral nerve stimulation (PNS) pulse sequence

Alternating trapezoidal bipolar gradient waveforms of 1-msec flat-top duration and varying rise-times (100, 200, 400, 600 and 1000 μsec) and amplitudes (at intervals of approximately 3% or 6% of peak amplitude of 200 mT/m per-axis) were used for the PNS test, similar to that used previously (9). A series of 128 waveform periods were played per second, and repeated for four times before stepping to the next higher amplitude. The test proceeded in order of increasing rise-times, with axes played in random order. Subjects were instructed to press a squeeze-ball when they were certain of any PNS sensation, at which time the test was paused and they would be surveyed to ascertain the anatomical location and subjective description of the sensation; these findings were confirmed at the conclusion of the entire PNS study.

Each subject first underwent the above PNS test at the “fixed” table position, which was defined as the furthest allowable position in the superior direction. Subsequently, the subject was displaced approximately 2 cm in the inferior direction for a shorter “displaced” table position test at rise-times (200, 400 μsec only). The “displaced” test was repeated at 4 cm inferior, and at 2 cm posterior and 4 cm posterior (0 cm inferior), yielding a total of four “displaced” tests. The data from both “fixed” and “displaced” positions were denoted as “all”.

Image Analysis

To more accurately determine the offset positions of each “displaced” position from the “fixed” position, image registration with Elastix (28) using rigid transformation and normalized mutual information cost function was performed between each pair of “fixed” vs. “displaced” T₁-weighted 3D image volumes. Each pair of image registration yielded three translation and three rotation parameters, which were used in subsequent regression analysis.

To provide a reference of the anatomy to the gradient system, anatomical landmarks were manually selected on the T₁-weighted sagittal images. These landmarks included the most superior extent of the brain (top of brain), the glabella, the most inferior extent or base of the cerebellum, and the C1/C2 interspace of the cervical spine. The superior/inferior (S/I, S is positive) and anterior/posterior (A/P, A is positive) positions were recorded. Visibility of the C2/C3 interspace was used as a visual indicator of the adequacy of linear brain coverage.

All twenty subjects completed the “fixed” position study, but only sixteen completed the “displaced” position study. Two subjects (31-year male and 55-year female) were not tested at the inferior “displaced” positions as the C2/C3 could not be visualized. One subject (53-year female) was tested in all but the furthest inferior position. One subject (38-year female) was tested in all but both posterior positions due to inadequate scan time.

PNS model

Logistic regression using the R statistical package version 3.5.2 (The R Foundation) was used for fitting PNS as a function of rise-times (τ), gradient amplitude (ΔG). The model for the binary output PNS, S may be defined as:

$$S=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{1\tau +}{\beta }_2\text{Δ}G\right)}}$$ (Eq. 3)

where ${\beta }_m,m\in \left\{0,1,2\right\}$ are the coefficients of the model. The minimum PNS-inducing zero-to-peak gradient amplitude, ΔG_min, chronaxie C, and minimum slew rate SR_min (slope of the ΔG-τ curve) are related by ΔG_min = SR_min × C, and their mean values in relation to the coeffcients are:

$$\overline{\mathrm{\Delta }{G}_{min}}=-\frac{{\beta }_0}{{\beta }_2},\overline{C}=\frac{{\beta }_0}{{\beta }_1}\text{ and }\overline{S{R}_{min}}=-\frac{{\beta }_1}{{\beta }_2}.$$ (Eq. 4)

To include an additional N fitting parameters ${\varphi }_n,n\in \left\{1,2,\dots ,N\right\}$, an additional 2N coefficients are added to S, which becomes:

$$S=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{1\tau }+{\beta }_2\text{Δ}G+{\sum }_{n=1}^N\left({\beta }_{1+2n}\varphi {\text{'}}_n+{\beta }_{2+2n}\varphi {\text{'}}_n\tau \right)\right)}},$$ (Eq. 5)

where ${\varphi }_n^{\prime }={\varphi }_n-{\overline{\varphi }}_n$, and ${\overline{\varphi }}_n$ is defined as the population mean of parameter n, with the exception of the image registration parameters where ${\overline{\varphi }}_n$ is set to zero. This centers ΔG_min, C, and SR_min about the population mean and at the “fixed” position. The parameters include age, gender or sex (+1 for male, −1 for female), translation parameters, and anatomical positions. These parameters were included in the model as linear and mixed effects of rise-time. The ΔG_min, C, and SR_min can then be defined as linear functions of these parameters as:

$$\mathrm{\Delta }{G}_{min}\left({\varphi }_n\right)=\overline{\mathrm{\Delta }{G}_{min}}+{\sum }_n^N{\alpha }_{\mathrm{\Delta }G,n}{\varphi }_n,C\left({\varphi }_n\right)=\overline{C}+{\sum }_n^N{\alpha }_{C,n}{\varphi }_n,\text{ and }S{R}_{min}\left({\varphi }_n\right)=\overline{S{R}_{min}}+{\sum }_n^N{\alpha }_{SR,n}{\varphi }_n,$$ (Eq. 6)

where the coefficients of these parameters are:

$${\alpha }_{\mathrm{\Delta }G,n}=-\frac{{\beta }_{1+2n}}{{\beta }_2},{\alpha }_{C,n}=\frac{{\beta }_{2+2n}}{{\beta }_1}\text{ and }{\alpha }_{SR,n}=-\frac{{\beta }_{2+2n}}{{\beta }_2}.$$ (Eq. 7)

Diffusion imaging

In two subjects (M, ages=40, 44 years), axial multi-shell diffusion imaging (b=0, 1000, 2000 sec/mm², 40-directions total) was performed only on the MAGNUS 3.0T system. Two scans were performed. The first was at “whole-body” performance level (derated to G_max=80 mT/m, SR=200 T/m/sec, and with the lower whole-body PNS limits) with parallel imaging acceleration factor R=2 (echo spacing=972 μsec, TE=67.2 msec, readout amplitude=23.4 mT/m). The second was at MAGNUS performance level (G_max=200 mT/m, SR=500 T/m/sec with MAGNUS PNS limits) with no parallel imaging (echo spacing=496 μsec, TE=37.4 msec, readout amplitude=45.2 mT/m), resulting in a similar extent of spatial distortion and readout SNR (within 2% difference). The other imaging parameters were kept constant (TR=4 sec, FOV=23.4 cm, 1.3-by-1.3 mm in-plane resolution, 3-mm slice-thickness). The same 8-channel head receiver coil was used. Gradient nonlinearity correction of diffusivity (29) was necessary due to the smaller linear FOV of head-gradients (30). Multi-shell, model-based denoising (31) was applied in generating diffusivity (mean, radial, parallel, and fractional anisotropy (FA)) and kurtosis maps (mean, radial, parallel, FA) (32). Fourteen small (29–202 mm²) white-matter ROIs were selected manually, twice per-image (to reduce bias), and on the colorized FA maps (left/right motor hand/feet, internal capsule, arcuate fasciculi, optic radiation, inferior longitudinal fasciculi, genu and splenium). As a measure of noise-to-contrast ratio, the mean-normalized standard deviation values for each diffusivity and kurtosis measurement were compared using two-sample t-test.

RESULTS

Electric field comparison

Fig.2 compares the E-field simulations inside the human body model in the coronal and sagittal planes. Across the whole body and in all gradient axes, the E-field for C3T (mean of 0.025–0.580 V/m) was slightly lower but not statistically different than that of MAGNUS (0.040–0.107 V/m), with the largest difference seen for the Z-axis. Across the head regions for the E-fields of C3T and MAGNUS were not significantly different (mean of 0.086–0.103 V/m in X-axis, 0.09–0.108 in Y-axis, 0.138–0.141V/m in Z-axis).

Figure 2.

Electric field (|E|) simulations generated from 100 T/m/sec slew rate waveforms for Compact 3T gradient and the MAGNUS gradient, in all three axes (top row=X, middle=Y, bottom=Z). Each figure panel shows the maximum intensity projection in the coronal and sagittal planes. Sections with bone (including vertebrae, skull, teeth, mandible), cartilage, cerebrospinal fluid were masked to better display the distribution in the musculature and other soft tissues.

Peripheral nerve stimulation – “fixed” position

Fig.3 shows a summary of the scatter plots of the onset of reported sensation recorded for each axis at the “fixed” position, along with the logistic regression fit and hardware limit of MAGNUS. The corresponding plots from the C3T are included for comparison (9). The MAGNUS X-axis fit (ΔG_min =111±6 mT/m, chronaxie, C=766±76 μsec, SR_min=145±7 T/m/sec) overlapped well with the C3T’s (ΔG_min =98.6±31.2 mT/m, C=611±448 μsec, SR_min=161±106 T/m/sec), and was also the most-sensitive axis. All but one subject registered at least one instance of PNS response for the X-axis. The MAGNUS Z-axis (ΔG_min =123±7 mT/m, C=620±62 μsec, SR_min=199±9 T/m/sec) was the second most-sensitive; all subjects registered at least one PNS response. Also, the MAGNUS Z-axis fit trended well to the scatter plots from the C3T Z-axis, for which there was inadequate data for fitting. The MAGNUS Y-axis was the least sensitive, with only 30% of subjects registering any PNS response, rendering the data inadequate for regression.

Figure 3.

Results of fixed position peripheral nerve stimulation study for (a) X-, (b) Y-, and (c) Z-axes for MAGNUS, with hardware specifications, and fitted PNS curves. Results are included results from that of the Compact 3T in Ref. (9). Zero-to-peak gradient amplitude are plotted against rise-times.

The anatomical locations of PNS sensation varied across all subjects for the same axis, if sensation was perceived (Table 1). X-axis stimuli were mostly facial (including forehead, nose, and lower facial regions), with the highest instances at the nose. Z-axis stimuli were mostly at the upper torso and neck (including shoulders, anterior and posterior chest regions), with the highest instances at the shoulders. The highest instances of subjective responses were “tingling” and “vibration”. Only in one subject (27-year female) was stimuli (X-axis, nose) described as “uncomfortable” and “painful”, but the subject voluntarily elected to continue the study and clarified that the “pain was mild”.

Table 1.

Summary of anatomical locations and subjective descriptions for instances of PNS (out of a maximum of N=20 subjects). The subjective senstations were collected across all axes. One or more anatomical locations and senstations per subject were recorded.

Position of PNS Instances/Axis	X-axis	Y-axis	Z-axis	Subjective Sensation	Instances
None	1	14	0	Tingling	9
Forehead	2	0	0	Pinching	1
Nose	12	0	0	Pressure	8
Between or near eyes	5	0	0	Vibration	9
Cheeks	4	0	1	Itching	1
Teeth/Gums	2	0	0	Throbbing	1
Face	1	0	0	Fluttering	1
Ears	3	1	0	Aching	2
Neck	0	2	2	Swelling	1
Shoulders	0	1	10	Uncomfortable	1
Back (Posterior)	0	2	2	Pain	1
Chest (Anterior)	0	1	9

In both X- and Z-axes stimulation, the amplitudes and locations of stimuli were fairly consistent, meaning that the amplitude vs. rise-time was approximately linear for the same subject. However, for the Y-axis even the stimuli recorded in Fig.1 and Table 1 were either inconsistent and nonlinear. For instance, in two subjects, stimuli registered responses only at ΔG=16.8 mT/m at τ=1000 μsec, but none at τ=600 μsec.

Peripheral nerve stimulation – “all” positions

Tables 2 and 3 summarize the ΔG_min and SR_min results for the X- and Z-axes respectively. The values were obtained with both “fixed” and “all” data, fitting with various permutations of the demographic and positional parameters. In all cases, mean ΔG_min and SR_min (and C) were statistically significant (p<0.001); the addition of demographic and positional parameters did not significantly alter these values (within 99% confidence interval (CI)). With age, X-axis ΔG_min increased by 1.4–1.8 mT/m/year while SR_min increased by 2.2–2.8 T/m/sec/year; Z-axis SR_min increased by 1.7–2.5 T/m/sec/year. The differences due to sex were statistically-significant only in SR_min and in most models (males higher by 30–42 T/m/sec in X-axis, 28–36 T/m/sec in Z-axis). Translation in the superior/inferior direction increased/reduced X-axis ΔG_min by 0.7–1.0 mT/m but reduced/increased X-axis SR_min by 3.0–3.1 T/m/sec, and reduced/increased Z-axis SR_min by 1.1 T/m/sec-per-mm. Translation in the anterior/posterior direction had smaller effects, reducing/increasing only Z-axis SR_min by 1.3–1.4 T/m/sec-per-mm.

Table 2.

Summary of X-axis (left-right) ΔG_min and SR_min fitting values for “fixed” position data, “all” positions data, and their linear coefficients (α) of demographic (gender, age) and positional parameters (image registration, top-of-brain, glabella, C1/C2 interspace, cerebellar base, S/I – superior (positive) - inferior (negative) direction, A/P – anterior (positive) - posterior (negative) direction), using logistic regression (P-values indicated if statistically significant). The Compact 3T (C3T) fitting values from Ref. (9) are included for comparison.

Data	Parameters, ϕ	$\overline{\mathrm{\Delta }{G}_{min}}$ (mT/m)	$\overline{S{R}_{min}}$ (T/m/s)	αΔG,Age (mT/m/yr)	αSR,Age (T/m/s/yr)	αΔG,Sex (mT/m)	αSR,Sex (T/m/s)	αΔG,S1 (mT/m/mm)	αSR,S1 (T/m/s/mm)	αΔG,AP (mT/m/mm)	αSR,AP (T/m/s/mm)
C3T	-	98.6 ±31	161±106	-	-	-	-	-	-	-	-
“Fixed”	-	111±6 (P<0.001)	145±7 (P<0.001)	-	-	-	-	-	-	-	-
“Fixed”	Sex, Age	104±6 (P<0.001)	155±7 (P<0.001)	+1.43±0.61 (P<0.05)	+2.46±0.70 (P<0.001)	−14.6±10.5	+34.6±12.6 (P<0.01)	-	-	-	-
“All”	Registration S/I and A/P	130±6 (P<0.001)	137±7 (P<0.001)	-	-	-	-	+0.98±0.40 (P<0.05)	−3.05±0.63 (P<0.001)	−0.59±0.47	+0.79±0.74
“All”	Sex, Age, Registration S/I, A/P	117±6 (P<0.001)	152±7 (P<0.001)	+1.37±0.46 (P<0.01)	+2.78±0.63 (P<0.001)	−5.32±8.60	+30.8±11.4 (P<0.01)	+0.73±0.29 (P<0.05)	−3.00±0.56 (P<0.001)	−0.24± 0.21	+0.42±0.67
“All”	Sex, Age, Top-of-Brain S/I, A/P	116±5 (P<0.001)	161±7 (P<0.001)	+1.59±0.52 (P<0.01)	+2.23±0.72 (P<0.01)	−2.80±9.50	+30.4±12.6 (P<0.05)	+0.04±0.23	−0.85±0.33 (P<0.01)	−2.06±0.25 (P<0.001)	+2.65±0.75 (P<0.001)
“All”	Sex, Age, Glabella S/I, A/P	119±5 (P<0.001)	161±7 (P<0.001)	+1.70±0.51 (P<0.001)	+2.35±0.69 (P<0.001)	−12.0±10.5	+42.2±14.2 (P<0.01)	+0.46±0.21 (P<0.05)	−1.24±0.31 (P<0.001)	−1.44±0.22 (P<0.01)	+2.64±0.64 (P<0.001)
“All”	Sex, Age, C1/C2 S/I, A/P	115±5 (P<0.001)	160±7 (P<0.001)	+1.84±0.54 (P<0.001)	+2.20±0.74 (P<0.01)	+2.6±10.0	+25.0±13.4	−0.16±0.23	−0.54±0.32	−1.10±0.19 (P<0.01)	+0.70±0.54
“All”	Sex, Age, Cerebellar S/I, A/P	113±5 (P<0.001)	161±7 (P<0.001)	+1.47±0.52 (P<0.01)	+2.30±0.72 (P<0.01)	−0.82±9.56	+29.6±12.8 (P<0.05)	−0.18±0.20	−0.58±0.28 (P<0.05)	−1.13±0.21 (P<0.01)	+0.34±0.61

Model: $\mathrm{\Delta }{G}_{min}\left({\varphi }_n\right)=\overline{\mathrm{\Delta }{G}_{min}}+{\sum }_n^N{\alpha }_{\mathrm{\Delta }G,n}{\varphi }_n$, and $S{R}_{min}\left({\varphi }_n\right)=\overline{S{R}_{min}}+{\sum }_n^N{\alpha }_{SR,n}{\varphi }_n$

Table 3.

Summary of Z-axis (left-right) ΔG_min and SR_min fitting values for “fixed” position data, “all” positions data, and their linear coefficients (α) of demographic (gender, age) and positional parameters (image registration, top-of-brain, glabella, C1/C2 interspace, cerebellar base, S/I – superior (positive) - inferior (negative) direction, A/P – anterior (positive) - posterior (negative) direction), using logistic regression (P-values indicated if statistically significant).

Data	Parameters, ϕ	$\overline{\mathrm{\Delta }{G}_{min}}$ (mT/m)	$\overline{S{R}_{min}}$ (T/m/s)	αΔG,Age (mT/m/yr)	αSR,Age (T/m/s/yr)	αΔG,Sex (mT/m)	αSR,Sex (T/m/s)	αΔG,S1 (mT/m/mm)	αSR,S1 (T/m/s/mm)	αΔG,AP (mT/m/mm)	αSR,AP (T/m/s/mm)
“Fixed”	-	123±7 (P<0.001)	199±9 (P<0.001)	-	-	-	-	-	-	-	-
“Fixed”	Sex, Age	117±7 (P<0.001)	207±9 (P<0.001)	−0.36±0.60	+2.46±0.80 (P <0.01)	−17.4±12.4	+36.8±16.4 (P <0.05)	-	-	-	-
“All”	Registration S/I and A/P	126±7 (P<0.001)	202±9 (P<0.001)	-	-	-	-	+0.30±0.31	−1.08±0.48 (P<0.05)	−0.61±0.36	−1.39±0.57 (P<0.05)
“All”	Sex, Age, Registration S/I, A/P	120±6 (P<0.001)	208±8 (P<0.001)	+0.14±0.42	+1.76±0.62 (P<0.01)	+4.00±8.58	+17.6±12.8	+0.23±0.29	−1.14±0.45 (P<0.05)	−0.51±0.17	−1.30±0.54 (P<0.05)
“All”	Sex, Age, Top-of-Brain S/I, A/P	123±5 (P<0.001)	214±7 (P<0.001)	+0.20±0.45	+1.70±0.68 (P<0.05)	−3.62±9.30	+28.2±13.8 (P<0.05)	+0.01±0.20	−0.10±0.31	+1.08±0.20 (P<0.01)	−2.05±0.64 (P<0.01)
“All”	Sex, Age, Glabella S/I, A/P	120±5 (P<0.001)	215±7 (P<0.001)	+0.05±0.44	+2.05±0.66 (P<0.01)	−1.2±10.1	+32.2±15.0 (P<0.05)	−0.07±0.19	−0.18±0.30	+0.70±0.20	−1.75±0.61 (P<0.01)
“All”	Sex, Age, C1/C2 S/I, A/P	121±5 (P<0.001)	214±7 (P<0.001)	+0.29±0.47	+1.92±0.71 (P<0.01)	+0.10±9.76	+31.2±14.6 (P<0.05)	+0.39±0.21	−0.61±0.32	+0.09±0.17	−1.14±0.52 (P<0.05)
“All”	Sex, Age, Cerebellar S/I, A/P	120±5 (P<0.001)	215±7 (P<0.001)	+0.27±0.46	+1.65±0.69 (P<0.05)	+0.16±9.28	+27.2±14.0	+0.21±0.18	−0.32± 0.28	+0.14±0.19	−1.27±0.59 (P<0.05)

Model: $\mathrm{\Delta }{G}_{min}\left({\varphi }_n\right)=\overline{\mathrm{\Delta }{G}_{min}}+{\sum }_n^N{\alpha }_{\mathrm{\Delta }G,n}{\varphi }_n$, and $S{R}_{min}\left({\varphi }_n\right)=\overline{S{R}_{min}}+{\sum }_n^N{\alpha }_{SR,n}{\varphi }_n$

The patterns for anatomical positions were similar to that of translation for the X-axis. The X-axis superior/inferior coefficients were smaller in magnitude (SR_min: from −0.6 to −1.2 T/m/sec-per-mm). The X-axis anterior/posterior coefficients were statistically significant but had opposing ΔG_min vs SR_min effects (ΔG_min: from −1.1 to −2.1 mT/m-per-mm, SR_min: from +0.3 to +2.7 T/m/sec-per-mm). In the Z-axis, the patterns for anatomical positions were similar to that of translation mostly only in SR_min. The Z-axis superior/inferior coefficients were not statistically significant. The Z-axis anterior/posterior dependencies also had opposing ΔG_min vs SR_min effects (ΔG_min: from +0.1 to +1.1 mT/m-per-mm, SR_min: from −1.1 to −2.1 T/m/sec-per-mm).

As shown in Table 4, S/I anatomical positions were highly correlated to the translation in S/I (r²=0.95–0.99), as were the A/P anatomical positions to the translation in A/P (r²=0.80–0.94). There was some cross-correlation between the AP/SI-anatomical positions to translations in AP/SI (r²=0.31–0.43), as well as to the rotation in the X-direction (R/L) (r²=0.09–0.39). Correlation against the other image registration parameters were weak (r²<0.03). The range of translation in S/I for “displacement in A/P” positions (95% CI=−5.6 to −0.6 mm), the range of translation in A/P for “displacement in S/I” positions (95% CI=−1.5 to −0.7 mm), and the range of rotation about the R/L-axis (95% CI =−0.9 to +1.1°) were fairly small. The range of rotation in A/P-axis (95% CI =+0.2 to +0.9°), S/I-axis (95% CI =−0.4 to +0.6°) and translation in R/L direction (95% CI=−1.1 to +0.3 mm) were even smaller. These results suggest that during the experiments, subject head positions were mostly confined to the sagittal plane. Fig.S3 and Fig. S4 respectively show examples of scatter plots of glabella SI- and AP-anatomical positions to the registration parameters.

Table 4.

Correlation (r²) values of anatomical landmarks’ S/I and A/P positions against the image registration parameters (rotations θ and translation in R/L, A/P and S/I).

Landmark / Parameter	θR/L	θA/P	θS/I	R/L	A/P	S/I
Top of Brain S/I	0.194	0.003	0.002	0.004	0.430	0.994
Top of Brain A/P	0.361	0.001	0.004	0.001	0.881	0.423
Glabella S/I	0.390	0.017	0.006	0.019	0.313	0.994
Glabella A/P	0.274	<0.001	0.004	0.002	0.937	0.427
C1/C2 S/I	0.178	0.002	0.043	0.019	0.411	0.959
C1/C2 A/P	0.09	0.002	0.002	0.002	0.806	0.338
Cerebellum S/I	0.338	0.010	<0.001	0.027	0.392	0.951
Cerebellum A/P	0.189	0.007	0.007	0.010	0.927	0.420

The coefficients from regression using “all” data with demographic and image registration parameters (see Tables 2–3 for PNS values) were used to predict PNS. The predicted effects from demographics are shown in Fig.4(a–b). Within the MAGNUS hardware operating region, PNS thresholds were slightly higher for males than females of the same age in both X- and Z-axes. For an assumed age difference of 30 years, the effect on rise-times at full-amplitude of 200 mT/m was larger in the X-axis (~600 μsec) than in the Z-axis (~200 μsec). The effects of positioning are shown in Fig.4(c–d). In X-axis PNS, an inferior shift by 20 mm reduces rise-time at full-amplitude by ~300 μsec. In the Z-axis, an inferior or posterior shift by 20 mm reduces rise-time by an order of magnitude smaller (~300 μsec).

Figure 4.

Effects of demographics (gender and age) on X-axis (a) and Z-axis (b) PNS, keeping constant mean inferior and posterior positions at zero, and effects of positioning in the inferior (I) or posterior (P) directions by 20 mm on X-axis (c) and Z-axis (d) PNS (mean age=40.4 years, mean of males and females).

Correlation between electric field simulation and experimental data

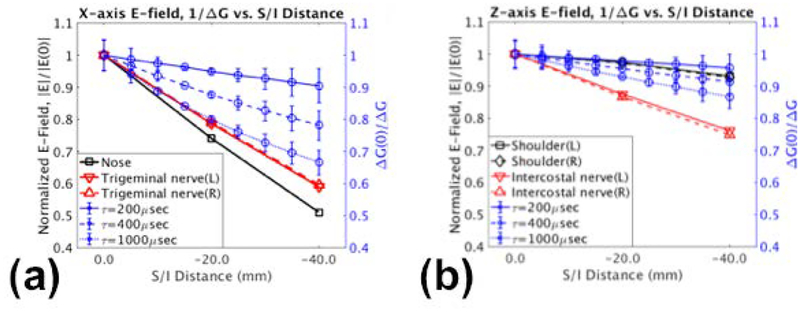
Fig.5 shows the effects of displacement in the inferior direction in the E-field simulations. Reduced E-field was observed with X-axis PNS (Fig.5a), and to a lesser extent in Z-axis PNS (Fig.5b), whereby the regions of interests were selected in the sagittal planes for the nose, trigeminal/maxillary nerves (facial stimulation), shoulders, and intercostal nerves at the T5-T6 vertebral interspace (anterior chest stimulation). These regions correspond approximately to the major stimulation anatomies from the PNS study (Table 1). For comparison, the inverse of the experimentally-found PNS thresholds obtained using the fitted registration parameters of Tables 2–3 were also plotted. The inverse of the thresholds is an analogue to the E-field obtained at various rise times typical to MRI pulse sequences (200–1000 μsec). While the E-field vs. distance plots did not overlap exactly with the inverse of the PNS, the trends of decreased X-axis E-fields with increased inferior-distance agreed well with the experimentally-found trend of increased stimulation thresholds; this was especially true at larger rise times. The effects in Z-axis were less pronounced than in the X-axis, but also agreed with the experimental results. Fig.S5 shows the E-field maps in both axes and the selected regions of interests.

Figure 5.

Effects of displacement in the superior/inferior (S/I) on the electric fields normalized to the 0.0 mm position (|E(0)|) at various anatomical regions are plotted against distance for the (a) X-axis and (b) Z-axis. The inverse of normalized stimulation levels (ΔG(0)/ΔG) obtained by fitting experimental data at various rise times (τ) are also plotted, showing good correlation with the electric field simulations.

Imaging results

In all measures of diffusivity and kurtosis, the mean-normalized standard deviation was lower in MAGNUS-performance than in whole-body performance in two-sample t-tests; these were statistically significant in mean diffusivity (by 34.7%, p<0.001), radial diffusivity (by 24.8%, p<0.001), parallel diffusivity (by 14.4%, p=0.004), mean kurtosis (by 26.9%, p<0.001), FA kurtosis (by 13.2%, p=0.026), radial kurtosis (by 22.0%, p<0.001), and parallel kurtosis (by 20.3%, p<0.001). The regions-of-interest (ROIs) were not statistically different (whole-body ROIs were smaller by 2.6 mm², paired t-test p=0.43). The diffusivity and kurtosis measures were not statistically different between MAGNUS and whole-body in two-sample tests; in paired t-test, there were small differences (−2.5% to +5.3%, p<0.005). The number of slices per TR in MAGNUS was higher than in whole-body by 29%.

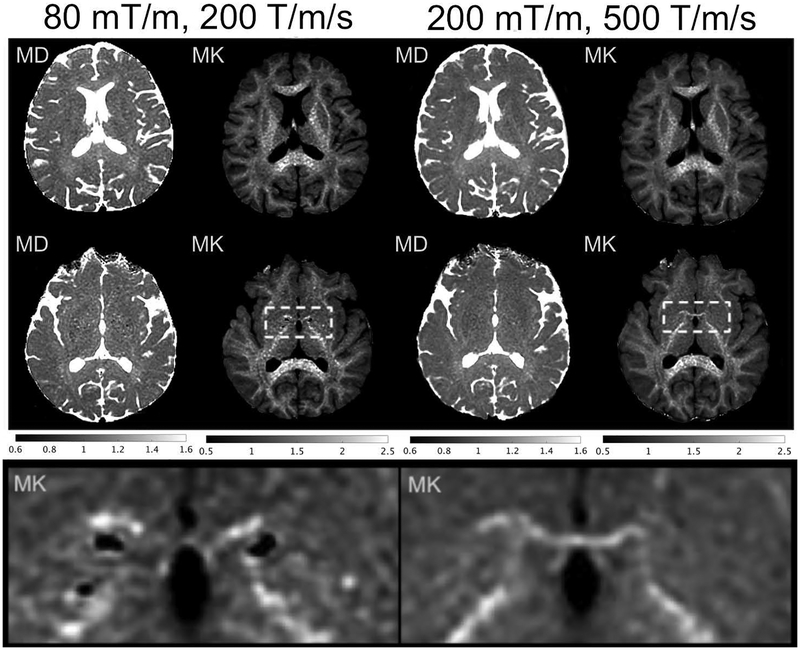
Fig.6 shows mean diffusivity and kurtosis from the two subjects, where the noise in the maps were visibly lower in MAGNUS than in the whole-body MRI scanner. Both subjects were imaged at approximately 2-cm inferior to the most superior positions. Neither subject experienced PNS.

Figure 6.

Mean diffusivity (MD) in μm²/msec and mean kurtosis (MK) maps obtained from multishell-diffusion from two subjects (top row: subject 1, middle row: subject 2, bottom row: subject 2 inset), with whole-body performance and PNS (80 mT/m, 200 T/m/sec, TE=67.2 msec), vs. MAGNUS performance and PNS (200 mT/m, 500 T/m/sec, TE=37.4 msec) on a b_max=2000 sec/mm² multishell sequence. Bottom row: close-up of rectangular ROI from subject 2, showing improved visualization of anterior commissure and reduced granularity of mean kurtosis maps.

DISCUSSION

In this work, the PNS thresholds of the high gradient amplitude (200 mT/m), high gradient slew rate (500 T/m/sec) MAGNUS head-gradient were investigated, demonstrating similar threshold levels to the Compact (C3T) head-gradient, which had previously been shown to be much higher than whole-body thresholds (5,9). Further, the effects of positioning in MAGNUS were also investigated and verified in comparison to E-field simulations, demonstrating increased PNS thresholds from reduced E-field primarily by displacement in the inferior direction. PNS thresholds increased significantly with age. At the MAGNUS gradient performance and PNS thresholds, the image quality of diffusivity maps was shown to be significantly better than that at whole-body performance. MAGNUS also had higher slice-efficiency, excluding gradient heating and power considerations, which would favor MAGNUS because of the smaller current needed for EPI readouts.

Statistical regression of the PNS thresholds could be performed for the X- and Z-axes on the MAGNUS, whereas that for only the X-axis could be done on the C3T (9,20). This was primarily due to the higher available gradient amplitude on MAGNUS as compared to the C3T. Like the C3T, X-axis PNS threshold was the lowest in MAGNUS gradient (i.e., most sensitive to PNS). Limited Y-axis stimulation was also observed on MAGNUS. This observation corresponded well with the visibly lower Y-axis E-field simulations as compared to the X-axis in the anterior facial regions. While the E-field maps suggest that MAGNUS thresholds could be slightly lower than that of the C3T’s, this was not determined experimentally. The MAGNUS PNS test also did not utilize the same subject pool as the C3T.

The hot spots on the MAGNUS E-field maps correlated well with the PNS study, namely facial stimulation for the X-axis, and shoulder/chest stimulation for the Z-axis. The effects of displacement in the superior/inferior direction also demonstrated good agreement between the E-field simulations and experimental PNS data. This suggests displacing the subject out of the magnet slightly could be a simple way to mitigate X-axis PNS. Displacements in the A/P direction did not alter PNS significantly. The anatomical landmarks in S/I and A/P, as well as R/L rotation correlated strongly with the displacements in S/I and A/P; the coefficients for fitting were however mostly smaller in the anatomical positions than for the displaced distances. This suggests that re-positioning by lowering and or tilting the head of the patient subject in the sagittal plane would not be as effective as moving the patient table for mitigating X- and Z-axes PNS.

In interpreting the correspondence between E-field and PNS, normalized values were used. This assumes that the E-field scaled proportionately with the slew rate, which was verified (simulation results not shown) for the range of frequencies (100–1000 Hz) typical to most MRI pulse sequences. In Fig.5(b–c), the effects of displacement were stronger at larger rise times. This implied that the fitted coefficients for SR_min were more important than that for ΔG_min in mitigating PNS by displacement in the inferior direction.

The simulations did not include a nerve model like that performed elsewhere (19), which potentially could have allowed for a linear integration along specific nerve bundles to provide better anatomical specificity. In this study, male PNS thresholds were slightly higher, contrary to another head-gradient study (19). However, in our study the differences were deemed to be small, especially in contrast to the effects due to age and positioning. Furthermore, there was a large diversity in the anatomical regions for PNS sensation, as well as in the subjective descriptions. This study also found strong correlations of PNS with age. It would be of interest to combine these together with a moiety of human body models and nerve aging models to better predict PNS across a diverse population. Furthermore, the availability of higher gradient performance in vivo raises further MRI safety-related questions about its impact on gradient-induced heating in implants (33), presence of implants on PNS, and risks of cardiac stimulation (12,34); these questions motivate the need for more research into accurate and sophisticated E-field and stimulation modeling.

The impact of higher gradient performance (G_max and SR) was evaluated with standard diffusion preparation (single spin-echo), whereby the primary effects for image quality improvement were reduction in echo time from higher gradient amplitude, and reduced EPI echo spacing. In addition to these benefits, the diffusion pulse width (δ) was reduced from 12.2 msec to 6.3 msec, which meant the MAGNUS acquisition was more sensitive to smaller microstructures; using an extra-axonal model (35), the correlation length $l_c~\sqrt{\delta }$, which means the sensitivity resolution of MAGNUS acquisition would be better by 40%. As compared to whole-body PNS, the shorter ramp times from the head-PNS of MAGNUS could have a significant contribution to reducing pulse widths; at 200 mT/m amplitude this translates to about 1.5 msec shorter per ramp. While standard single spin-echo uses only four ramps, other variations of diffusion-encoding such as twice-refocused spin-echo (36), double diffusion encoding (37,38), oscillating gradient spin-echo (39), and q-space imaging (40,41) utilize far more ramps and hence would benefit more from a higher head-PNS threshold.

In conclusion, the head-PNS thresholds of the MAGNUS head-gradient experimentally determined in this study were similar to that of the Compact head-gradient. The PNS threshold could be further increased by small displacements of the subjects in the inferior direction. The PNS thresholds provided by the MAGNUS gradient were in good agreement with E-field simulations. As compared to state-of-the-art whole-body MRI, the higher gradient performance and PNS threshold of MAGNUS provided higher contrast-to-noise ratio in diffusion MRI, and should provide increased sensitivity to smaller microstructure length scales.

Supplementary Material

Supp figS1-5

Figure S1. MAGNUS gradient main magnetic fields i.e. B_z (a-d) and electric field magnitude maps (e-h) at 10 mT/m gradient amplitude and 1 kHz, shown as contour plots in the coronal (top row, X- and Z-axes) and sagittal planes (bottom row, Y- and Z-axes). The plots show the fields in the patient-accessible space. The designed field-of-view of 26 cm is depicted by the dashed circle. The internal outline of the MAGNUS gradient is marked by the shaded area.

Figure S2. MAGNUS X-axis gradient coil free-space E-field (a) that is proportional to the A-field at 10 mT/m gradient amplitude and 1 kHz (slew rate of 62.8 T/m/s), conductivity (b) and the resulting E-field from the same coronal mid-plane (c), and the resulting maximum intensity projection (MIP) in the coronal plane (d).

Figure S3. Scatter plots and correlation (r²) values of the glabella anatomical landmarks’ S/I position against the image registration parameters (rotations θ and translation in R/L, A/P and S/I), with the lines indicating the linear fit and shaded regions indicating the standard error.

Figure S4. Scatter plots and correlation (r²) values of the glabella anatomical landmarks’ A/P position against the image registration parameters (rotations θ and translation in R/L, A/P and S/I), with the lines indicating the linear fit and shaded regions indicating the standard error.

Figure S5. Effects of displacement in the superior/inferior (S/I) on the electric fields (|E|). Maximum intensity projections of electric field simulations in coronal and sagittal orientations, for X-axis (top row) and Z-axis (bottom row) at 0, 20 and 40 mm displacements in the inferior direction (left to right). Sections with bone (including vertebrae, skull, teeth, mandible), cartilage, cerebrospinal fluid were masked to better display the distribution in the musculature and other soft tissues. Regions of interests (green) selected in nose, trigeminal/maxillary nerves, shoulders and intercostal nerves are shown.