A Nontrigonal Tricoordinate Phosphorus Ligand Exhibiting Reversible ‘Nonspectator’ L/X–Switching

Abstract

We report here a ‘nonspectator’ behavior for an unsupported L-function σ³–P ligand (i.e. P{N[o-NMe-C₆H₄]₂}, 1a) in complex with the cyclopentadienyliron dicarbonyl cation (Fp⁺). Treatment of 1a•Fp⁺ with [(Me₂N)₃S][Me₃SiF₂] results in fluoride addition to the P-center, giving the isolable crystalline fluorometallophosphorane 1a^F•Fp that allows a crystallographic assessment of the variance in the Fe–P bond as a function of P-coordination number. The nonspectator reactivity of 1a•Fp⁺ is rationalized on the basis of electronic structure arguments and by comparison to trigonal analogue (Me₂N)₃P•Fp⁺ (i.e. 1b•Fp⁺), which is inert to fluoride addition. These observations establish a nonspectator L/X-switching in (σ³–P)–M complexes by reversible access to higher-coordinate phosphorus ligand fragments.

Graphical Abstract

An L-function trivalent phosphorus ligand accepts fluoride ion by nucleophilic addition to generate a stable, isolable metallophosphorane; the reaction is reversible. Changes to the metal–phosphorus bonding as a function coordination number at P are analyzed crystallographically and computationally.

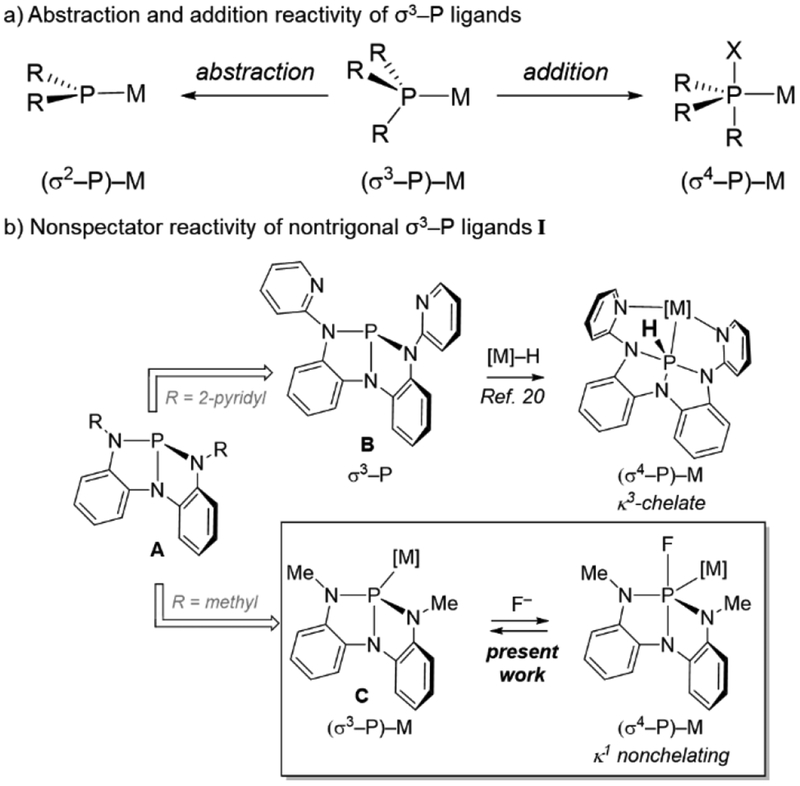
Tricoordinate phosphorus (σ³–P) compounds are archetypal donor ligands in coordination chemistry.^1,2,3 Within the Covalent Bond Classification,^4,5 σ³–P compounds are designated L-function ligands for transition metals (M) and are overwhelmingly construed as inert, ancillary, spectator ligands within (σ³–P)–M complexes. A rich ‘nonspectator’ reaction chemistry of metal-bound σ³–P compounds, however, belies this prevailing view. Abstraction of a P-substituent from (σ³–P)–M complexes accesses dicoordinate phosphorus ligands (Figure 1a; σ²–P^–, phosphide; σ²–P⁺, phosphenium),⁶ and the σ²–P^+/–/σ³–P interconversion has been the focus of extensive stoichiometric^{7,8,9,10,11,12,13} and catalytic¹⁴ investigation. By complement, addition of an exogenous nucleophile to phosphorus in an L-function (σ³–P)–M complex increases the P-coordination number, resulting in a ‘metallophosphorane’ complex with an X-function (σ⁴–P)–M formula.¹⁵ Literature concerning the addition of a P-substituent to (σ³–P)–M complexes to give higher-coordinate phosphorus congeners is comparatively sparse.¹⁶ Verkade has postulated that fluoride addition to Pd^II-(bis)phosphines induces Pd^II→Pd⁰ reduction via initial addition of F^– to P.¹⁷ Further, Nakazawa and Miyoshi have shown the possibility of nucleophilic substitution of P-substituents in cationic Fe^II-phosphite complexes, in some cases leading to persistent (σ⁴–P)–M products.^18,19

Figure 1.

Nonspectator modes of reactivity for (σ³–P)–M complexes.

Recently, a κ³-chelate containing a nontrigonal σ³–P center (Figure 1,B) was shown to access directly a (σ⁴–P)–M metallophosphorane by formal insertion to a Ru–H bond.²⁰ An interpretation of XANES data for B and related compounds A attributed the propensity of the phosphorus center to attain higher coordination to the presence of a low-energy P-based orbital made accessible by the nontrigonal local environment.²¹ The presence of the low-lying P-centered orbital in A and related compounds raised the prospect of accentuated intermolecular electrophilic reactivity of such nontrigonal σ³–P ligands. We report here the reversible addition of an exogenous nucleophile to the P-center of an unsupported (σ³–P)–M complex C that demonstrates a nonspectator behavior of ligands A. With this study, direct experimental evidence is provided that delineates: (1) the inherent electronic impact on metal-binding arising from nontrigonal distortion of σ³–P ligands without convolution from chelate effects, and (2) the direct crystallographic observation of a nonspectator phosphorus ligand in a higher-coordination state following exogenous nucleophile addition. The ability for nontrigonal σ³–P ligands to reversibly expand local coordination number while remaining σ-bound in the primary ligand sphere of a metal complex forecasts emerging opportunities for functional nonspectator ligands within (σ³–P)–M complexes.2²

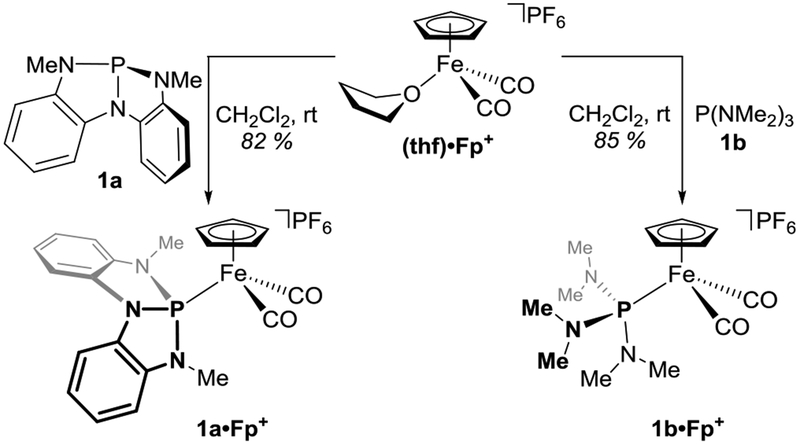
On the basis of precedent from Martin²³ and Nakazawa and Miyoshi,^18,19 the cyclopentadienyliron dicarbonyl cation (Fp⁺) was selected as a coordinatively saturated ‘ancillary metal’²⁴ fragment for study. Iron complexes 1a•Fp⁺ and 1b•Fp⁺ were prepared by ligand exchange of [thf•Fp][PF₆]²⁵ with P{N[o-NMe-C₆H₄]₂} (1a)^26,27 and (Me₂N)₃P (1b), respectively (Figure 2).

Figure 2.

Synthesis of [R₃P•Fp][PF₆] complexes, where R₃P = 1a or 1b.

According to IR spectroscopy, the CO stretching frequencies of 1a•Fp⁺ (ν_asym 2017 cm⁻¹, ν_sym 2061 cm⁻¹) are higher in energy than those of 1b•Fp⁺ (ν_asym 2000 cm⁻¹, ν_sym 2045 cm⁻¹). This trend tracks qualitatively with the J_Se-P coupling constants for phosphorus selenides 1a•Se (J_Se-P = 907 Hz) and 1b•Se (J_Se-P = 784 Hz), suggesting to a first approximation that 1a is a weaker σ-donor than 1b (see Table 1 for collected metrical data). The ⁵⁷Fe NMR chemical shifts (obtained indirectly by 2D Fe–P correlation solution NMR experiments due to the low receptivity of the ⁵⁷Fe nucleus²⁸) for 1a•Fp⁺ (δ 616 ppm) and 1b•Fp⁺ (δ 688 ppm) are consistent with this interpretation, based on trends established for related cyclopentadienyliron complexes.²⁹

Table 1.

Collected spectroscopic, structural, and computational data for compounds 1a, 1b, 1a•Fp⁺, 1b•Fp⁺, and 1a^F•Fp.

Metric	31P δ (ppm)a	1JP-Se (Hz)	57Fe δ (ppm)b	d(Fe1-P1) (Å)	ν(CO) (cm−1)	FIA (kcal/mol)c	EDA-NOCVd
							Etot	EPauli	Eestat	Esteric	Edisp	Eorb	σ(P→Fe)	π(P←Fe)
1a	160.4	907e	-	-	-	-	-	-	-	-	-	-	-	-
1b	122.4	784e	-	-	-	-	-	-	-	-	-	-	-	-
1a•Fp+	183.5	-	616	2.1809(4)	2017, 2061	59.3	−91.9	122.7	−105.0	17.7	−16.1	−93.6	−61.7	−18.1
1b•Fp+	141.4	-	688	2.2381(5)	2000, 2045	32.9	−99.8	130.0	−118.4	11.6	−18.4	−92.9	−65.8	−13.2
1aF•Fp	−3.0	-	1013	2.3047(9)	1952, 2007	-	-	-	-	-	-	-	-	-

^appm vs. 85% H₃PO₄.

^bppm vs. Fe(CO)₅.

^cComputed (BP86/def2-TZVP(CPCM=CH₂Cl₂) according to the method in Ref. 32.

^dEDA-NOCV computational results represent attractive and repulsive energies (kcal/mol) between the Fp⁺ fragment and phosphorus ligands at the fragment geometry of the complex. The direction of donation is defined to be from phosphorus to iron.

^eValues from Ref. 25.

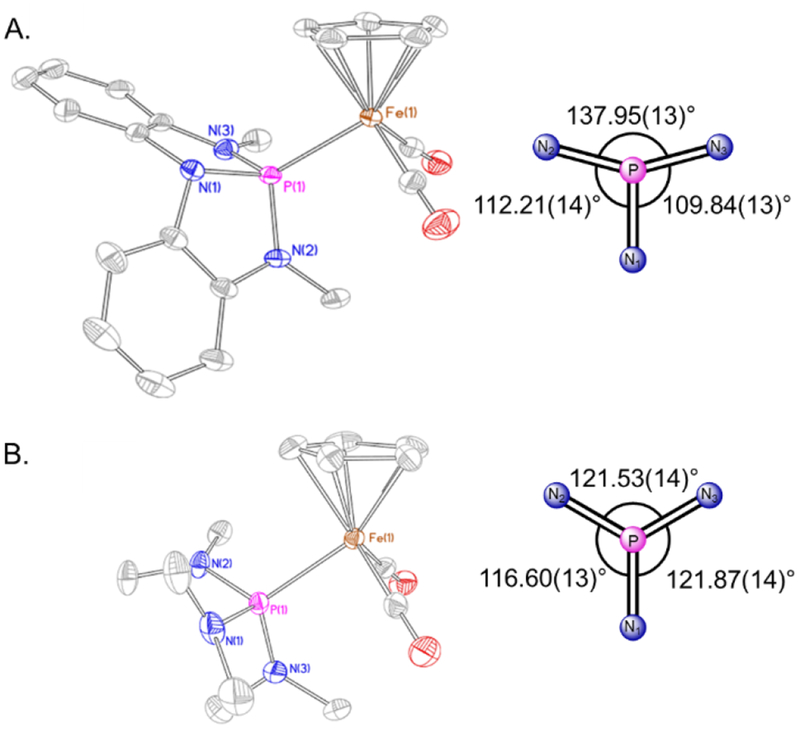
Further distinctions between 1a•Fp⁺ and 1b•Fp⁺ are manifest in structural analyses based on X-ray diffractometry data obtained with single-crystalline samples (Figure 3). Most evidently, compound 1a•Fp⁺ features a shorter Fe–P bond length (d_Fe–P = 2.1809(4) Å) as compared to compound 1b•Fp⁺ (d_Fe–P = 2.2381(5) Å). Also, consistent with the aforementioned vibrational data, the average Fe–C_CO bond length in 1a•Fp⁺ (d_Fe–C = 1.7886(17) Å) is slightly longer than in 1b•Fp⁺ (d_Fe–C = 1.7766(19) Å). A further feature of note concerns the dihedral angles φ(N-P-Fe-N); by projection down the P–Fe axis (Figure 3A, right), compound 1a•Fp⁺ shows a span of dihedral angles Ω(φ) = 28.11(26)°, with a maximum dihedral of φ(N₂-P-Fe-N₃) = 137.95(13)°. By contrast, compound 1b•Fp⁺ shows only a span of dihedral angles Ω(φ) = 5.3(3)° and a maximum dihedral of φ(N₁-P-Fe-N₃) = 121.87(14)°. These metrics illustrate the enhanced nontrigonal local geometry about phosphorus for 1a•Fp⁺ as compared to 1b•Fp⁺, consistent with the structural distinctions between the free ligands.²⁶ For reference, the N₂–P–N₃ bond angle of 1a•Fp⁺ (116.40(7)⁰) is almost unchanged from that of 1a (115.21(7)⁰), showing that complexation does not significantly perturb the phosphorus triamide framework.

Figure 3.

(A) Left: Thermal ellipsoid plot for 1a•Fp⁺ rendered at 50% probability level. Hydrogen atoms, noncoordinating PF₆^– counterion, and a THF solvent molecule are omitted for clarity. Selected metrical data for 1a•Fp⁺: d(Fe-P): 2.1809(4) Å, d(Fe-(CO)₁): 1.7879(17) Å, d(Fe-(CO)₂): 1.7893(16) Å, ∠(N₁-P-N₂): 93.42(6)⁰, ∠(N₁-P-N₃): 93.04(7)⁰, ∠(N₂-P-N₃): 116.39(7)⁰. Right: Schematic projection down the P–Fe axis for 1a•Fp⁺ illustrating dihedral angles φ(N-P-Fe-N). (B) Left: Thermal ellipsoid plot for 1b•Fp⁺ rendered at 50% probability level. Only one of two molecules in the asymmetric unit is depicted. Hydrogen atoms and a noncoordinating PF₆^– counterion are omitted for clarity. Selected metrical data for 1b•Fp⁺: d(Fe-P): 2.2381(5) Å, d(Fe-(CO)₁): 1.7739(19) Å, d(Fe-(CO)₂): 1.7792(18) Å, ∠(N₁-P-N₂): 101.59(8) ⁰, ∠(N₁-P-N₃): 105.03(9)⁰, ∠(N₂-P-N₃): 107.09(9)⁰. Right: Schematic projection down the P–Fe axis for 1b•Fp⁺ illustrating dihedral angles φ(N-P-Fe-N). See SI for full details.

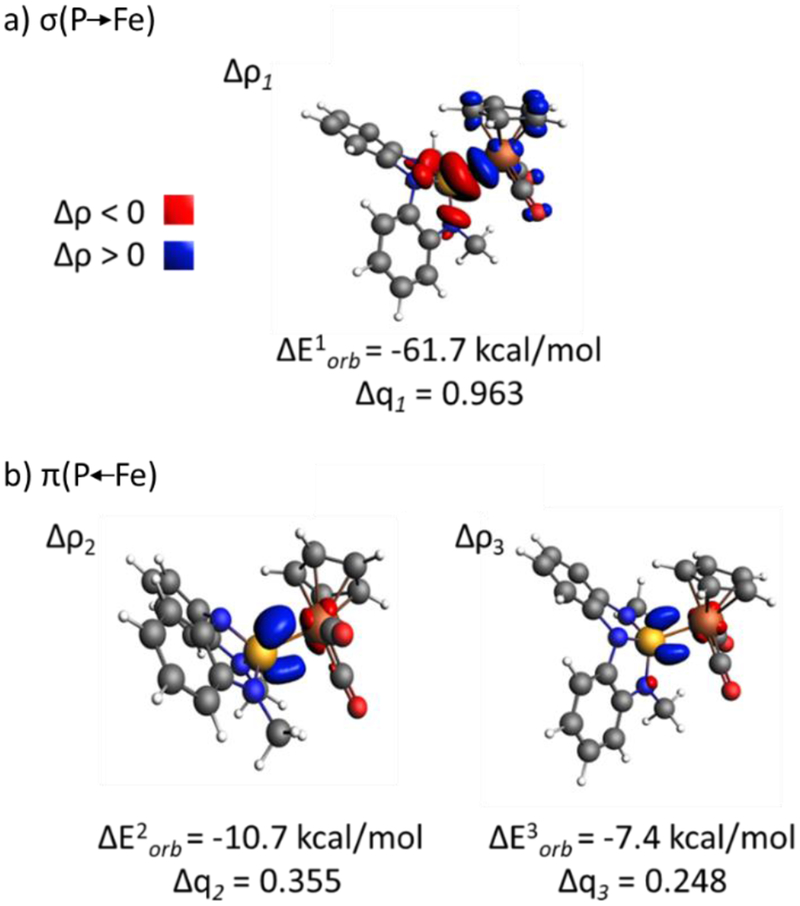
In an effort to parse the σ- and π- contributions to the Fe–P bonding interactions in 1a•Fp⁺ and 1b•Fp⁺, an energy partitioning into pairwise orbital interactions between σ³–P ligand (1a and 1b, respectively) and Fp⁺ fragments was undertaken with the Energy Decomposition Analysis – Natural Orbitals for Chemical Valence (EDA-NOCV) method³⁰ as implemented in the ADF modeling program³¹ at the BP86/def2-TZVP level of density functional theory (Table 1, see SI for full details). Along lines described by Michalak,³² deconvolution of the covalent bonding portion (E_orb) into σ- and π-symmetry components for 1a•Fp⁺ gives donation σ(P→Fe) = −61.7 kcal/mol (65.9% of E_orb) and back-donation π(P←Fe) = −18.1 kcal/mol (19.3% of E_orb). An illustration of the electron deformation densities for the three principal NOCV interactions of 1a•Fp⁺ is presented in Figure 4. NOCV deformation density channel Δρ₁ depicts depletion of electron density at P (red) and accrual of electron density at Fe (blue) as would be expected for an L-function σ-dative interaction. NOCV deformation density channels Δρ₂ and Δρ₃ correspond to the backflow of electron density from an Fe dπ orbital into P-based π-acceptor orbitals with two distinct interaction energies (ΔE²_orb = −10.7 kcal/mol, ΔE³_orb = −7.35 kcal/mol), consistent with the lifting of pπ degeneracy at nontrigonal 1a shown by previous XAS evidence.²¹ By way of comparison, EDA-NOCV partitioning of the Fe–P bond in 1b•Fp⁺ gives donation σ(P→Fe) = −65.8 kcal/mol (70.8% of E_orb) and back-donation π(P←Fe) = −13.2 kcal/mol (14.2% of E_orb). This analysis therefore quantifies the relatively weaker σ-donating ability of nontrigonal σ³–P compound 1a as compared to a compositionally related phosphorous triamide 1b evident from spectroscopy (vide supra). Further, a combined consideration of the spectroscopic, structural, and theoretical data suggests a relatively stronger π-accepting ability of 1a vs. 1b.

Figure 4.

Contours of electron deformation density channels Δρ₁, Δρ₂, and Δρ₃ describing the bonding between 1a and the Fp⁺ metal fragments with corresponding energies and charge estimations obtained from EDA-NOCV method.

To quantify the relative electrophilicity of P-based acceptor orbitals for 1a•Fp⁺ vs. 1b•Fp⁺, solvation-corrected fluoride ion affinities (FIAs) were computed at the M06L/def2-TZVP(CPCM:CH₂Cl₂) level of theory by isodesmic reaction enthalpies according to Christe’s method.³³ The FIA for 1a•Fp⁺ is computed to be significantly larger (–ΔH = 59.3 kcal/mol) than that for 1b•Fp⁺ (–ΔH = 32.9 kcal/mol). The low absolute values for the FIAs are indicative a modest overall fluoride affinity,³⁴ but the difference Δ(FIA) = 26.4 kcal/mol conforms to the interpretation that P-based electrophilic reactivity should be favored at the nontrigonal complex 1a•Fp⁺.

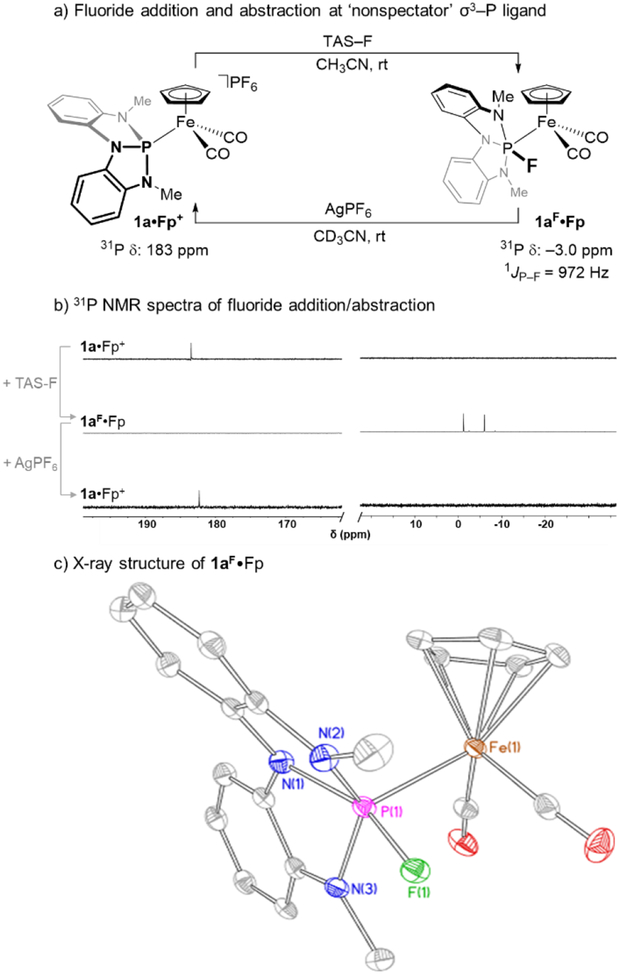
The reactivity of 1a•Fp⁺ and 1b•Fp⁺ toward fluoride addition was probed experimentally. Treatment of compound 1a•Fp⁺ with tris(dimethylamino)sulfonium trimethyldifluorosilicate (TASF) in acetonitrile resulted in an immediate change in color from yellow to deep orange (Figure 5a). The formation of a single new phosphorus-containing species was evident by ³¹P NMR spectroscopy, as indicated by the doublet resonance at δ −3.0 ppm, which displayed large scalar coupling (J = 971 Hz) consistent with the presence of a single fluorine bound to phosphorus via a direct P–F bond. The large upfield shift in ³¹P NMR chemical shift is consistent with an increased coordination number at phosphorus by fluoride addition, and this inference is confirmed by observation of the complementary coupling in the lone ¹⁹F NMR resonance (δ 27.4 ppm, J = 971 Hz, Figure 5b). The product was thus assigned to be fluorometallophosphorane 1a^F•Fp, in which a fluoride has been added to the phosphorus of 1a•Fp⁺ to generate a neutral complex. In solution, compound 1a^F•Fp exhibits time-averaged molecular C_s-symmetry with a persistent P–Fe bond;¹³C NMR spectra demonstrate an equivalence of the CO ligands (one resonance at δ 211 ppm) with well-resolved ²J_C–P = 49 Hz and ³J_C–F = 5.7 Hz coupling constants. Treatment of 1b•Fp⁺ to identical fluorinating conditions (TASF, MeCN, rt) does not result in fluorination but instead returns starting materials alongside some decomposition of 1b•Fp⁺. It is evident that fluoride addition to a higher coordinate phosphorus ligand is enabled by the enhanced electrophilicity of 1a•Fp⁺ as compared to 1b•Fp⁺.

Figure 5.

A) Reversible fluorination of 1a•Fp⁺ and the resulting fluorometallophosphorane 1a^F•Fp. B) Solution ³¹P NMR spectra in CD₃CN: (top) spectrum of 1a•Fp⁺; (middle) spectrum of 1a^F•Fp from addition of TASF to 1a•Fp⁺; (bottom) spectrum of 1a•Fp⁺ following treatment of 1a^F•Fp with AgPF₆ and removal of precipitate (AgF). C) Thermal ellipsoid plot rendered at 50% probability level for 1a^F•Fp. Hydrogen atoms are removed for clarity. Relevant metrical data for 1a^F•Fp: d(Fe-P): 2.3047(9) Å, d(P-F): 1.6687(18) Å, ∠(N₁-P-F): 158.11(12)⁰, ∠(N₂-P-N₃): 134.91(13)⁰, ɸ(C₂-Fe-P-F) = 2.63⁰, ɸ(C₁-Fe-P-N₃) = 8.12⁰. See SI for full details.

The air and moisture sensitive orange 1a^F•Fp can be crystallized by slow evaporation of a saturated CH₂Cl₂ solution at −35° C (Figure 5c). X-ray diffractometry confirms the structural assignment of 1a^F•Fp as a metallophosphorane resulting from addition of an exogenous fluoride to σ³–P ligand 1a without further substitution. With respect to the Fe bonding environment, compound 1a^F•Fp features an increased Fe–P bond length (d_Fe–P = 2.3047(9) Å) as compared to 1a•Fp⁺, as well as a shorter average Fe–C_CO bond length (d_Fe–C = 1.764(3) Å) that coincides with a bathochromic shift of the carbonyl stretching frequencies (ν_asym 1952 cm⁻¹, ν_sym 2007 cm⁻¹). With respect to the P bonding environment, metrical parameters give a geometry index of τ = 0.35, indicating a geometry closer to that of a square pyramid than a trigonal bipyramid.³⁵ The addition of fluoride results in an increase in all of the P–N bond lengths by 0.05 Å < Δd_P–N < 0.09 Å as is common for higher-coordinate main group compounds that compensate for their formal ‘hypervalent’ character by distribution of electron density toward the substituents.³⁶ The P–F bond length is quite long (d_P–F = 1.6687(18) Å), but falls within the range (1.64(11) Å < d_P–F < 1.69(1) Å) observed for the only prior example of a structurally characterized fluorometallophosphorane (i.e. Ir(CO)Cl₂(PEt₃)₂(PF₄)) from Holloway.³⁷

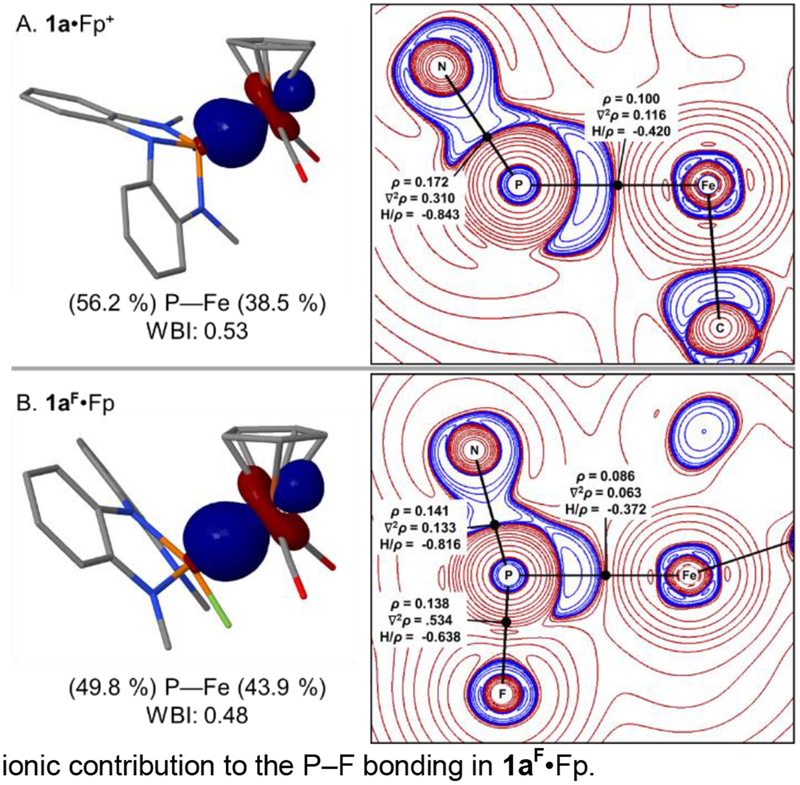
Bonding analysis in 1a•Fp⁺ and 1a^F•Fp reveals changes to the nature of the Fe–P σ-interactions as a function of fluoride binding. NBO analysis reports a dative covalent P→Fe σ-interaction for 1a•Fp⁺ described by an NLMO comprising modest polarization toward the phosphorus (P 56.2%/Fe 38.5%; Figure 6a, left) and involving a P donor NBO with sp^1.10 hybridization. The NLMO corresponding to the P–Fe bonding interaction in 1a^F•Fp indicates an increased distribution across Fe–P (P 49.8%/Fe 43.9%; Figure 6b, left) with similar phosphorus parentage (sp^1.16). Moving from 1a•Fp⁺ to 1a^F•Fp, the Wiberg bond indices decrease (1a•Fp⁺: WBI = 0.53; 1a^F•Fp: WBI = 0.48), in line with the observed increase in bond length from crystallography (Δd_P–Fe = +0.12 Å). For comparison, similar qualitative trends are reported by Gabbai for addition of fluoride to antimony in Pt-Sb bimetallics.³⁸ Here, we invoke a decreased importance of π-backbonding effects in 1a^F•Fp to account for this observation; the P-based acceptor orbital is saturated by addition of exogenous fluoride and unavailable for metal bonding.

Figure 6.

Bonding analysis for 1a•Fp⁺ and 1a^F•Fp. (A) Left: NLMO representing P–Fe bond for 1a•Fp⁺. Right: Contour plot of the Laplacian of the electron-density topology1a•Fp⁺ in the plane containing the Fe, P, and N atoms. Areas of charge depletion are depicted in red and areas of charge concentration are depicted in blue. Black dots indicate bond critical points. Metrics represent relevant properties at the bond critical points (ρ in e/ų, ∇²ρ in e/Å⁵, H/ρ in atomic units). (B) Left: NLMO representing P–Fe bond for 1a^F•Fp. Right: Contour plot of the Laplacian of the electron-density topology 1a^F•Fp in the plane containing the Fe, P, and F atoms.

Topological analysis of the computed electron density within the Quantum Theory of Atoms in Molecules (QTAIM) framework³⁹ returns bond paths defined by (3, −1) critical points for P–Fe in 1a•Fp⁺ (Figure 6a, right), and both P–Fe and P–F in 1a^F•Fp (Figure 6b, right). No bond paths were located for any F…Fe or N…Fe trajectory, conforming to an η¹-formulation of metallophosphorane 1a^F•Fp. Qualitatively, P-based valence shell charge concentrations are evident in the Laplacian of the electron density for both 1a•Fp⁺ and 1a^F•Fp along the P–Fe bond path, in line with an L- and X-function ligand classification, respectively. By contrast, the Laplacian distribution for the P–F bond is indicative of a ‘closed-shell interaction’ and a dominant ionic contribution to the P–F bonding in 1a^F•Fp.

Consistent with the ionic character of the P–F bonding interaction, treatment of 1a^F•Fp with fluoride abstracting reagents leads to removal of the F^– ligand and regeneration of 1a•Fp⁺. Specifically, the addition of 1 equiv of AgPF₆ to a CD₃CN solution of 1a^F•Fp induces the orange solution to become yellow with immediate formation of precipitate. Following filtration, ³¹P NMR spectroscopy (Figure 5b) confirms full consumption of 1a^F•Fp and clean return of compound 1a•Fp⁺. Evidently, both the nontrigonal phosphorus framework and the P–Fe bond are sufficiently robust as to be retained during the course of the nonspectator L→X→L-switching cycle.

The data reported herein define the spectroscopic, structural, and electronic changes that accrue to phosphorus ligand 1a as it undergoes increase in coordination number upon exogenous fluoride addition. The conversion from L- to X- function roles results in little change to the donor capacity of the phosphorus ligand, but the acceptor capacity is diminished. Further, the reversible nonspectator behavior of tricoordinate phosphorus ligand 1a calls to mind recent developments for higher valent states of Sb ligands from Gabbaï.²² Given this periodic relationship within group 15, the broader implications of nonspectator L/X switching for phosphorus-based ligands in catalysis and sensing warrant further investigation.