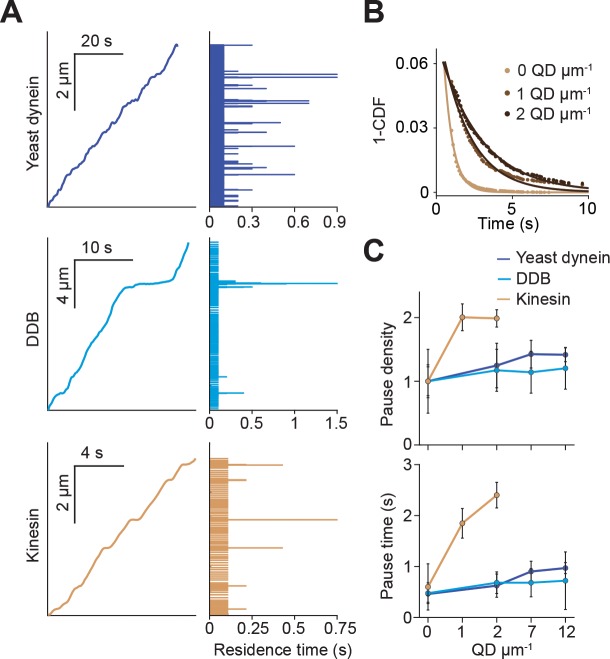
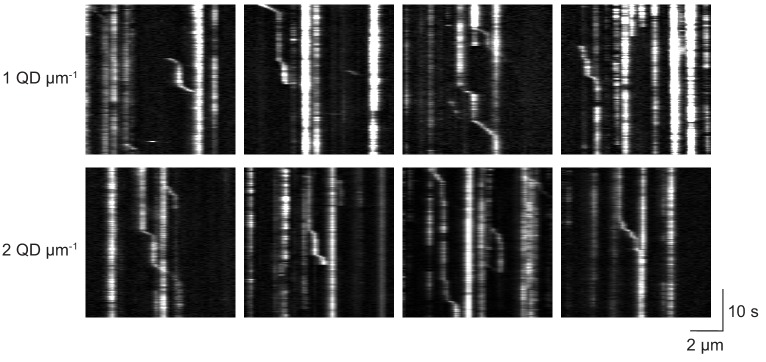
Figure 2. Kinesin pauses more frequently than dynein when encountering QD obstacles.

(A) (Left) Representative traces of yeast dynein, DDB, and kinesin in the absence of QD obstacles on surface-immobilized MTs. (Right) Residence times of the motors in each section of the traces. (B) The inverse cumulative distribution (1-CDF) of kinesin residence times at different obstacle concentrations were fit to a single exponential decay. The residuals of that fit (shown here) are fit to a single exponential decay (solid line) to calculate the density and duration of kinesin pausing. (C) Density and duration of the pauses of the three motors. Pause densities (pauses/µm) are normalized to the 0 QDs µm⁻¹ condition. Kinesin pausing behavior at 7 and 12 QDs µm⁻¹ could not be determined because the motor was nearly immobile under these conditions. From left to right, n = 535, 520, 158, 29 for yeast dynein, 511, 449, 391, 276 for DDB, and 570, 127, 112 for kinesin. Error bars represent SEM calculated from single exponential fit to residence times.

Figure 2—figure supplement 1. Kinesin pauses in the presence of QD obstacles.

Representative kymographs reveal frequent pauses in kinesin motility in the presence of 1 QD µm⁻¹ (top row) or 2 QD µm⁻¹ (bottom row). Most pauses were permanent throughout recording. Processive traces interspersed with transient pauses were used in pause analysis in Figure 2.

Figure 2—figure supplement 2. Simulations for the pause analysis.

(A) An example trajectory simulated with a pause density of 0.8 µm⁻¹ in the absence of tracking noise (see Materials and methods for the parameters used to generate these trajectories). (B) An example trajectory simulated with 100 nm root mean squared (RMS) noise. (C) Localization error calculated for 1000 simulated traces closely agrees with 100 nm noise added to the traces. (D) Localization error calculated for 500 experimental traces of the three motors. (E) Optimization of the bin size and sliding window size for the pause analysis. Noisy traces were simulated using 0.8 µm⁻¹ pause density, down-sampled with given window size (the number of data points) and residence time was calculated for a given bin size (distance traveled by motor). The analysis revealed that pause density was slightly underestimated even under optimal conditions. The combination of bin size and window size that resulted in the highest pause density was used to analyze experimental traces. (F) Traces were simulated with a pause density of 0.3 µm⁻¹. Calculated pause density from simulations was insensitive to the 0–100 nm added tracking noise. The density of detected pauses decreases at higher noise. (G) The inverse cumulative distribution of pause density and duration were determined from residence time histograms through a two-step process. (Left) All non-zero residence times were fit to a single exponential distribution. (Right) Zoomed view of the blue rectangle on the left. The residuals of this fit (plotted in Figure 2B) were fit to a single exponential decay to determine pause time and density. (H) The pause density analysis of single motors on surface-immobilized MTs without normalization. From left to right, n = 535, 520, 158, 29 for yeast dynein, 511, 449, 391, 276 for DDB, and 570, 127, 112 for kinesin. Error bars represent SE calculated from single exponential fit to residence time histograms.