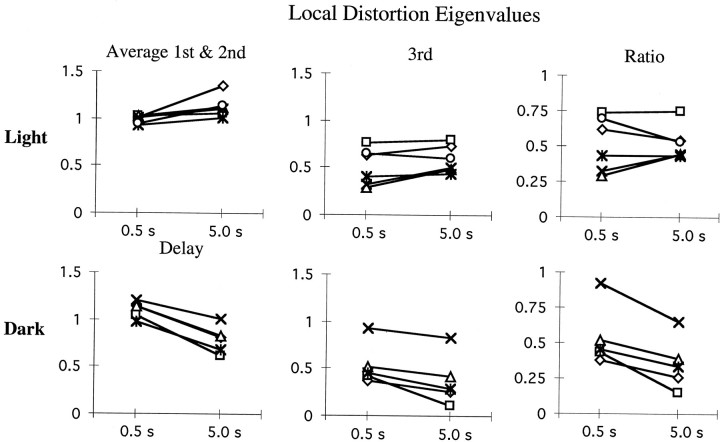
Fig. 7.

Eigenvalues of the local transformation estimate. Eigenvalues are unitless gains indicating spatial expansion or contraction in 3D target-to-endpoint mappings. Eigenvalues >1 indicate magnification of the local space along the corresponding eigenvector, whereas eigenvalues <1 indicate spatial contraction. First and second eigenvalues are averaged (left column) and compared with the third eigenvalue (center column) representing the amount of maximal contraction along the corresponding eigenvector. The right column shows the ratio of the third eigenvalue over the average of the first and second, indicating the amount of distortion introduced in the visuomotor transformation. Contraction is relatively constant in the light, whereas contraction increases with memory delay duration in the dark.