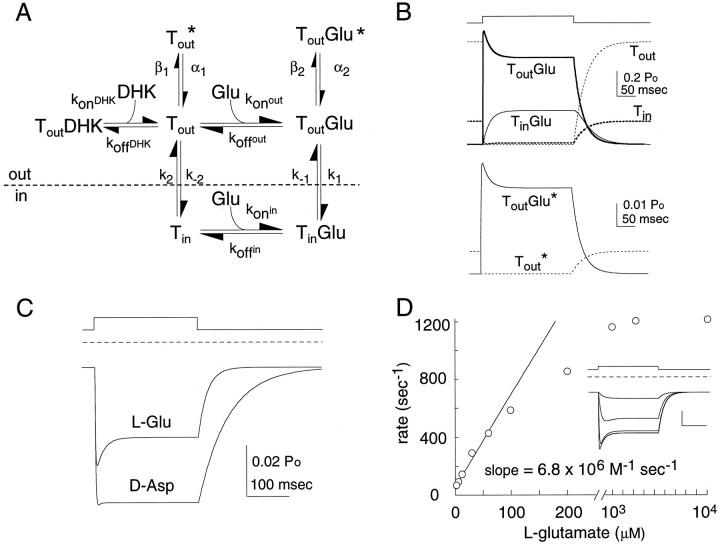
Fig. 8.

Computer simulation. A, Kinetic model of l-glutamate and d-aspartate transport and anion conductance. Model parameters were obtained by least squares fitting of data and fit an average pulse of l-glutamate ofd-aspartate. The microscopic rates were as follows:k_on^out = 6.8 × 10⁶m⁻¹sec⁻¹,k_off^out = 30.6 sec⁻¹; k₁ = 16.0 sec⁻¹; k₋₁ = 2.9 sec⁻¹;k_onⁱⁿ = 6.8 × 10⁶m⁻¹sec⁻¹;k_offⁱⁿ = 37.2 sec⁻¹; k₂ = 885 sec⁻¹; k₋₂ = 200 sec⁻¹; α₁ = 8094 sec⁻¹; β₁ = 100 sec⁻¹; α₂ = 1260 sec⁻¹; β₂ = 70 sec⁻¹. d-Aspartate data were fit with identical rates for agonist independent states andk_off^out = 7.6 sec⁻¹; k₁ = 7.3 sec⁻¹; k₋₁ = 1.0 sec⁻¹;k_offⁱⁿ = 165 sec⁻¹; α₂ = 978 sec⁻¹, and β₂ = 70 sec⁻¹. DHK binding was assigned as 6.8 × 10⁶m⁻¹sec⁻¹, whereas DHK unbinding (kdhk_out) = 97 sec⁻¹.B, Probability of occupancy for each state in the kinetic scheme shown in A during a 250 msec pulse of 10 mml-glutamate. The top traces show the nonconducting states: the unliganded states are represented bydashed lines (T_out andT_in; bold), whereas the liganded states are represented by a solid line(T_outGlu; bold andT_inGlu). The bottom traces show the occupancy of the anion conducting states. Note the different scale bars. C, Simulation of a 250 msec pulse of 10 mml-glutamate or d-aspartate (A). The channel’s steady-state open probability was determined from nonstationary noise analysis (Fig. 4) and the DHK-blocked currents (Fig. 6). The fraction of transporters in either conducting state TGlu_open orT_open are plotted as a function of time.D, Concentration dependence of the time constant for activation of l-glutamate currents for the kinetic scheme shown in A. The time constants for the activation and deactivation were calculated by fitting the current records to a single exponential. The limiting slope for the activation rate equals 6.8 × 10⁶m⁻¹sec⁻¹. Inset,l-Glutamate concentration dependence of the open probability (1 μm, 10 μm, 100 μm, and 1 mm). The model’s apparent affinity at steady state is 7 μm.