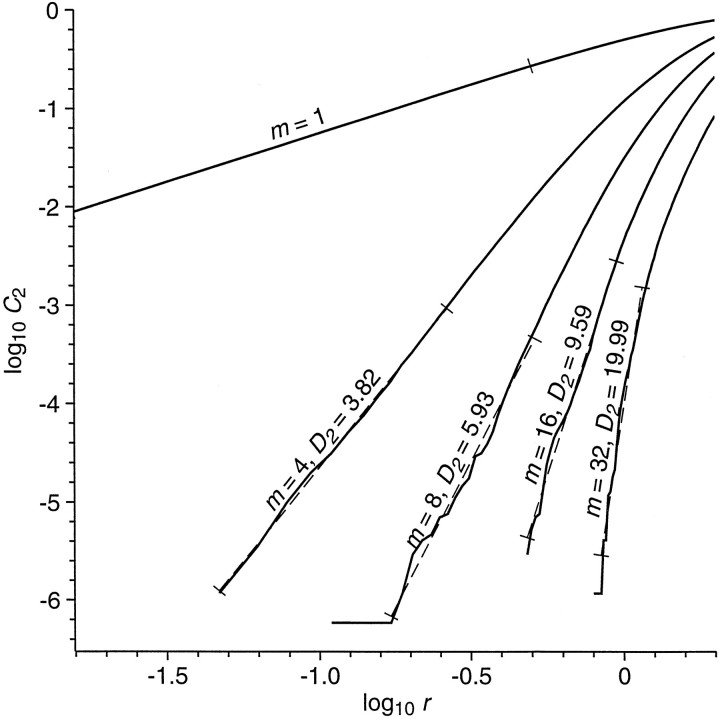
Fig. 3.
Log of correlation integralC2 as a function of log of radiusr, for various values of embedding dimensionm. The value of the correlation integral at radiusr is the average fraction of all points of the trajectory lying within an m-dimensional cube of radiusr, with the cube centered on a point on the trajectory. For ideal noise-free stationary low-dimensional systems, the log correlation integral should decrease linearly with decreasing log of radius at small radius; the slope of this scaling region is the correlation dimension, estimated here by the slope of the dashed straight lines fit to the curves. For curves at embedding dimension sufficiently greater than the correlation dimension, the slopes should saturate at a constant estimate of correlation dimension. The curves shown here, for a single 8 sec segment of EEG, are representative of many that show little evidence of a low-dimensional attractor but that nevertheless have slopes less than those for surrogates of the EEG.