Fig. 1.

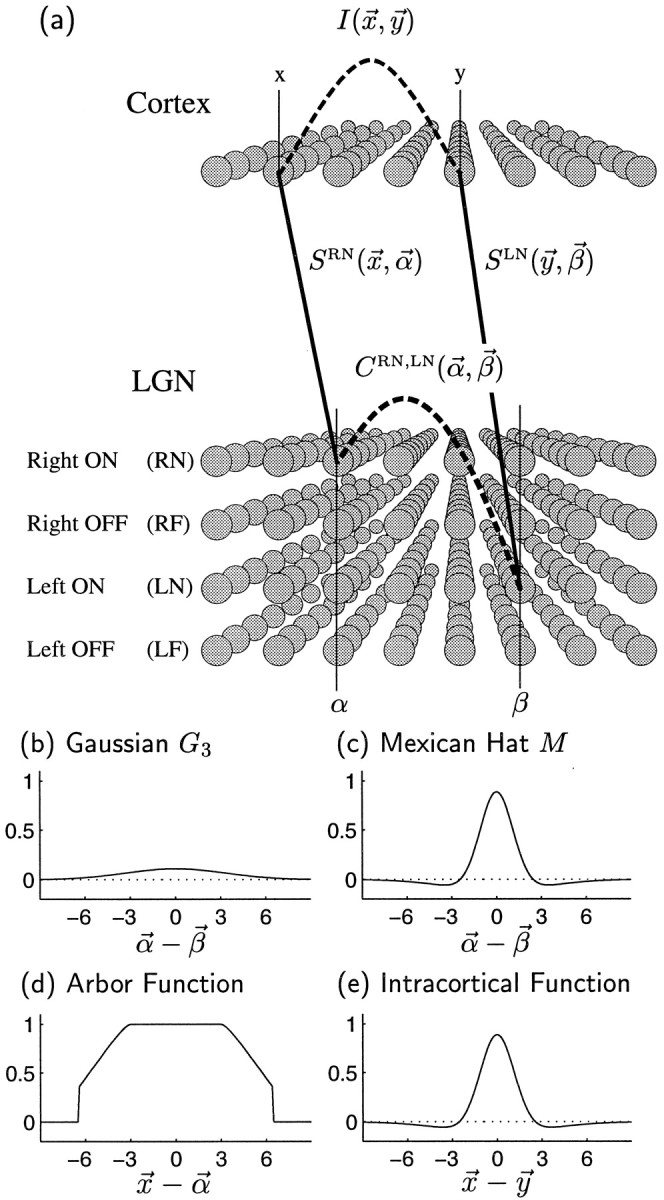
a, Sketch of the model. The synaptic weight variable S^RN(x⃗,α⃗) represents the total weight to cortical positionx⃗ from LGN cells at α⃗ representing eye R (right eye) of center type N (ON-center). Similarly, S^LN(y⃗, β⃗) represents the total left-eye, ON-center weight from β⃗ toy⃗. More generally, synaptic weights from α⃗ tox⃗ are written S^EC(x⃗,α⃗), where E represents eye, E ∈ {R, L} (right eye, left eye), and C represents center type, C ∈ {N, F} (ON center, OFF center). The correlation function C^RN,LN(α⃗, β⃗) measures the degree of correlation between the spiking activities of LGN neurons of type RN at position α⃗ and those of type LN at positionβ⃗. More generally, activity correlations between LGN neurons of type E, C at position α⃗, and those of type E′, C′ at position β⃗, are written C^EC,E′C′(α⃗, β⃗). The intracortical interaction function I(x⃗, y⃗) describes how activity at cortical location x⃗encourages or discourages the development of correlated synaptic connections at a nearby location y⃗. b, c, The correlation functions C^EC,E′C′(α⃗,β⃗) are defined in terms of two functions. b, A Gaussian function G₃(α⃗ − β⃗) (see Eq. 3) represents correlations that are purely positive and taper with distance; c, an oscillating or Mexican-hat function M(α⃗ − β⃗) (Eq. 4) represents correlations that change sign with distance. d, e, Arbor function A(x⃗ − α⃗) and the intracortical interaction function I(x⃗ − y⃗) used throughout this article. The horizontal axes are in units of grid intervals; 1 grid interval can be taken to be ∼100 μm (Miller, 1994). The vertical axes are in arbitrary units (changes in the size of A , I or C are equivalent to change in the size of the learning rate η (Eq. 2); hence the absolute size of these functions is arbitrary).