Figure 2.

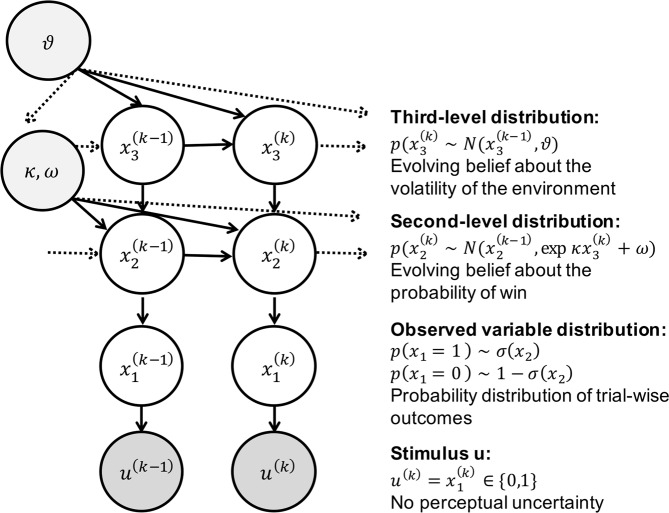
The Hierarchical Gaussian Filter (HGF): u^(k) represents binary observations (true wins = 1, and losses = 0, in the case of the slot machine). Binary inputs are represented on the first level, $x_1^{\left(k\right)}$ via a Bernoulli distribution, around the probability of win or loss, $x_2^{\left(k\right)}$. In turn, $x_2^{\left(k\right)}$ is modelled as a Gaussian random walk, whose step-size is governed by a combination of $x_3^{\left(k\right)}$, via coupling parameter κ, and a tonic volatility parameter ω. $x_3^{\left(k\right)}$ also evolves as a Gaussian random walk over trials, with step size ϑ (meta-volatility). In this investigation, after observing trial-wise outcomes (win or lose), the gambler updates her belief about the probability of win on a given trial k $(x_2^{\left(k\right)})$, as well as how swiftly that slot machine is moving between being ‘hot’ (high probability of win) or ‘cold’ (low probability of win) $x_3^{\left(k\right)}$. On any trial, the ensuing beliefs then provide a basis for the gambler’s response, which may be to increase the bet size, ‘double up’ after a win, switch to a new slot machine or leave the casino.