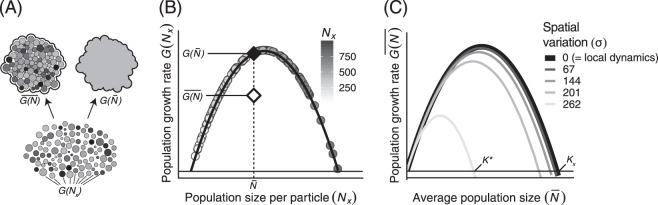
Fig. 3.

a Illustration of the concept of scaling-up local microbial community dynamics to quantify the behavior of an aggregate sample. Degree of shading denotes an OTU’s population sizes across a heterogeneous collection of particles governed by the shared, nonlinear dynamics, G(N_x), from Eq. 2. Note the conceptual differences between aggregating these data by averaging over the local nonlinear dynamics, $\overline{G\left(N\right)}$, and by fitting our small-scale dynamical model to the average population density, $G\left(\overline{N}\right)$. b The differences in these aggregation procedures result in differing estimates for scaled-up population dynamics. The black curve shows the logistic governing dynamics, G(N_x), of populations on individual particles (shaded circles). Note the difference in growth rates between the correctly spatially averaged growth function (white diamond) and growth function fit to the spatial average population density (black diamond). c Increasing the spatial variation of local populations results in vastly different spatially averaged population dynamics. Here again, the black line denotes the local dynamics, G(N_x), which equals the spatially averaged dynamics when there is no variation among subpopulations. For this concave-down function, increasing the spatial variation causes the scaled-up carrying capacity, K^*, to be smaller than the local carrying capacity, K_x