Abstract
Wall modelling in large-eddy simulation (LES) is necessary to overcome the prohibitive near-wall resolution requirements in high-Reynolds-number turbulent flows. Most existing wall models rely on assumptions about the state of the boundary layer and require a priori prescription of tunable coefficients. They also impose the predicted wall stress by replacing the no-slip boundary condition at the wall with a Neumann boundary condition in the wall-parallel directions while maintaining the no-transpiration condition in the wall-normal direction. In the present study, we first motivate and analyse the Robin (slip) boundary condition with transpiration (non-zero wall-normal velocity) in the context of wall-modelled LES. The effect of the slip boundary condition on the one-point statistics of the flow is investigated in LES of turbulent channel flow and a flat-plate turbulent boundary layer. It is shown that the slip condition provides a framework to compensate for the deficit or excess of mean momentum at the wall. Moreover, the resulting non-zero stress at the wall alleviates the well-known problem of the wall-stress under-estimation by current subgrid-scale (SGS) models (Jiménez & Moser, AIAA J., vol. 38 (4), 2000, pp. 605–612). Second, we discuss the requirements for the slip condition to be used in conjunction with wall models and derive the equation that connects the slip boundary condition with the stress at the wall. Finally, a dynamic procedure for the slip coefficients is formulated, providing a dynamic slip wall model free of a priori specified coefficients. The performance of the proposed dynamic wall model is tested in a series of LES of turbulent channel flow at varying Reynolds numbers, non-equilibrium three-dimensional transient channel flow and a zero-pressure-gradient flat-plate turbulent boundary layer. The results show that the dynamic wall model is able to accurately predict one-point turbulence statistics for various flow configurations, Reynolds numbers and grid resolutions.
Keywords: turbulence modelling, turbulent boundary layers, turbulent flows
1. Introduction
The near-wall resolution requirement to accurately resolve the boundary layer in wall-bounded flows remains a pacing item in large-eddy simulation (LES) for high-Reynolds-number engineering applications. Choi & Moin (2012) estimated that the number of grid points necessary for a wall-resolved LES scales as Re13/7, where Re is the characteristic Reynolds number of the problem. The computational cost is still excessive for many practical problems, especially for external aerodynamics, despite the favourable comparison with the Re37/14 scaling required for direct numerical simulation (DNS), where all the relevant scales of motion are resolved.
By modelling the near-wall flow such that only the large-scale motions in the outer region of the boundary layer are resolved, the grid-point requirement for wall-modelled LES scales at most linearly with increasing Reynolds number. Therefore, wall-modelling stands as the most feasible approach compared with wall-resolved LES or DNS. Several strategies for modelling the near-wall region have been explored in the past, and most of them are effectively applied by replacing the no-slip boundary condition in the wall-parallel directions by a Neumann condition. This fact is motivated by the observation that, with the no-slip condition, most subgrid-scale (SGS) models do not provide the correct stress at the wall when the near-wall layer is not resolved by the grid (Jiménez & Moser 2000).
Examples of the most popular and well-known wall models are the traditional wall-stress models (or approximate boundary conditions), and detached-eddy simulation (DES) and its variants. Approximate boundary condition models compute the wall stress using either the law of the wall (Deardorff 1970; Schumann 1975; Piomelli et al. 1989; Yang et al. 2015) or the Reynolds-averaged Navier-Stokes (RANS) equations (Balaras, Benocci & Piomelli 1996; Wang & Moin 2002; Chung & Pullin 2009; Kawai & Larsson 2013; Park & Moin 2014). DES (Spalart et al. 1997) combines RANS equations close to the wall and LES in the outer layer, with the interface between RANS and LES domains enforced implicitly through the change in the turbulence model. The reader is referred to Cabot & Moin (2000), Piomelli & Balaras (2002), Larsson et al. (2016) and Bose & Park (2018) for a more comprehensive review of wall-stress models and to Spalart (2009) for a review of DES.
One of the most important limitations of the models above is that they depend on pre-computed parameters and/or assume explicitly or implicitly a particular law for the mean velocity profile close to the wall. Recently this has been challenged by Bose & Moin (2014) with a dynamic slip wall model that is free of any a priori specified coefficients. In addition, the no-transpiration condition used in most wall models was replaced by a Robin boundary condition in the wall-normal direction. The present study extends the work by Bose & Moin (2014) and is divided in two parts. In the first part, we investigate the use of the slip boundary condition at the wall for the three velocity components in the context of wall-modelled LES. The motivation for the use of this boundary condition is corroborated both theoretically and through detailed a priori tests of filtered velocity fields. We then assess whether this condition is physically advantageous compared with other boundary conditions when the LES grid resolution is insufficient to accurately resolve the near-wall region. In addition, sensitivities of the slip boundary condition with respect to Reynolds number, grid resolution and SGS model in actual LES are explored. In the second part of the paper, we discuss the requirements for constructing wall models based on the slip condition and propose a dynamic procedure independent of any a priori tunable parameters, consistent with the slip boundary condition and based on the invariance of wall stress under test filtering.
The paper is organised as follows. In § 2, we present and motivate the suitability of the slip boundary condition for LES by considering the behaviour of the filtered velocities at the wall. A priori testing is performed on filtered DNS data to test the validity of the analysis. In § 3, we perform a set of turbulent channel LES with the slip boundary condition and study the effect of the slip parameters, choice of SGS model, grid resolution and Reynolds number on the one-point statistics such as the mean and root-mean-squared (r.m.s.) velocity profiles. A dynamic procedure is presented in § 4, and its performance is evaluated in § 5 for LES of two-dimensional and non-equilibrium three-dimensional transient turbulent channel flows and a zero-pressure-gradient flat-plate turbulent boundary layer. Finally, conclusions are offered in § 6.
2. Slip boundary condition with transpiration
We define the slip boundary condition with transpiration as
| (2.1) |
where repeated indices do not imply summation. The indices i = 1, 2, 3 denote the streamwise, wall-normal and spanwise spatial directions represented by x1, x2 and x3, respectively, ui are the flow velocities, is the resolved LES field (or filter operation), n is the wall-normal direction and (·)|w indicates quantities evaluated at the wall. The grid or filter size will be denoted as Δi for the respective directions. We define li to be the slip lengths and vi the slip velocities. In general, both the slip lengths and velocities are functions of space and time. A sketch of the slip boundary condition for a flat wall is given in figure 1. In this section, we provide theoretical motivation for the slip boundary condition in the context of filtered velocity components and inspect the validity of (2.1) using a priori testing of filtered DNS data. The physical implications of the slip lengths are also investigated in terms of the mean velocity profile and r.m.s. velocity fluctuations. Some preliminary results of this section can be found in Bae, Lozano-Durán & Moin (2016).
Figure 1.
Sketch of the slip boundary condition with transpiration for a flat wall.
2.1. Theoretical motivation
Let us consider a wall-bounded flow. For the Navier–Stokes equations, the velocity at the wall is given by the no-slip boundary condition (Stokes et al. 1901)
| (2.2) |
If we interpret LES as the solution of the filtered Navier–Stokes equations (Leonard 1975), the filtering operation in the wall-normal direction will result, in general, in non-zero velocities at the wall. For wall-resolved LES, where the effective filter size near the wall is small, can still be approximated by the no-slip boundary condition (Ghosal & Moin 1995). However, when the filter size is large or the near-wall resolution is coarse, such as in wall-modelled LES, a modified wall boundary condition different from the usual no-slip is required for the three velocity components. Consider a one-dimensional symmetric filter kernel with non-zero filter size defined by its second moment
| (2.3) |
Then, far from the wall , where x2 = 0 is the location of the wall, the filtered velocity field can be computed as
| (2.4) |
where x = (x1, x2, x3) and . However, in the near-wall region, the filter kernel in the wall-normal direction has a functional dependence on the wall-normal distance, which becomes prevalent for x2 → 0, as depicted in figure 2. The new filter operator restricted by the wall then becomes
| (2.5) |
where
| (2.6) |
is the effective (rescaled) kernel at a wall-normal distance x2.
Figure 2.
(Colour online) Sketch of the change in effective kernel approaching the wall.
Assuming a no-slip boundary condition for the unfiltered velocity and approximating the velocity profile near the wall as a Taylor expansion , the filtered velocity can be expressed as
| (2.7) |
where is the mth moment of , the effective filter at the wall. From (2.7), it can be shown that
| (2.8) |
Since and , we can use (2.7) and (2.8) to obtain a second-order approximation of the boundary condition of the form
| (2.9) |
where .
This boundary condition is exact for a linear velocity profile but is expected to deteriorate as the linear approximation is no longer valid for . In this case, the second- and higher-order terms excluded in (2.9) may result in different slip lengths and extra terms for each velocity component as in (2.1) to achieve an accurate representation of the flow at the wall. The particular expressions for li and vi depend formally on the filter shape, size and instantaneous configuration of the filtered velocity vector at the wall.
Equation (2.9) motivates the use of the slip boundary condition for wall-modelled LES. Nevertheless, it is important to highlight a few remarks regarding the derivation and the consistency of the slip condition. The first observation is that in the case of explicitly filtered LES (Lund & Kaltenbach 1995; Lund 2003; Bose 2012; Bae & Lozano-Durán 2017) with a well-defined filter operator, the filter size is a given function of the wall-normal distance, and the slip lengths and velocities can be computed explicitly. However, in the present study, we focus on traditional implicitly filtered LES, where the filter operator is not distinctly defined and, consequently, neither is the filter size, typically assumed to be proportional to the grid size. This supposed relation between the filter and grid sizes is not always valid (Lund 2003; Silvis et al. 2016) and worsens close to the wall. Therefore, in the near-wall region, it is reasonable to assume that the effective filter size is an unknown function of the wall-normal distance, and the slip lengths and velocities must be modelled as they cannot be computed explicitly. As a final remark, note that commutation of the filter and derivative operators is necessary to formally derive the LES equations, which, in turn, entails a constant-in-space filter size or a filter operator that is constructed to be commutative (Marsden, Vasilyev & Moin 2002). This condition is not met by (2.1), but given that the filter size for implicitly filtered LES is an unknown function of space, we also neglect terms arising from commutation errors.
2.2. A priori evaluation
A priori testing of the slip boundary condition is conducted to assess the validity of (2.1) in filtered DNS data of turbulent channel flow from Del Álamo et al. (2004), Hoyas & Jiménez (2006) and Lozano-Durán & Jiménez (2014a) at friction Reynolds numbers of Reτ ≈ 950, 2000 and 4200, respectively.
In the following, uτ is the friction velocity, v is the kinematic viscosity and the channel half-height is denoted by δ. Wall units are defined in terms of v and uτ and denoted by the superscript + and outer units in terms of δ and uτ. In each case, DNS velocity vector is filtered in the three spatial directions with a box-filter with filter size equal to Δ1 × Δ2 × Δ3. The resulting filtered data contain and , which can be used to test the accuracy of (2.1) by computing their joint probability density function (PDF).
The joint PDF for Reτ ≈ 950 with Δ1 = Δ2 = Δ3 are plotted in figure 3(a–c). The results show, on average, a linear correlation between and , which supports the suitability of the slip boundary condition given in (2.1) with vi = 0. However, the spread of the joint PDFs increases with increasing filter size. A trend similar to that of figure 3(a–c) appears when increasing the Reynolds number for a constant filter size Δi/δ (not shown), which implies that the second-order approximation deteriorates as the filter size increases in wall units. However, despite this scaling, a linear relationship between and is still satisfied on average, and it will be shown in § 3 that this is enough to obtain accurate predictions of the mean velocity profile in actual LES.
Figure 3.
(Colour online) Joint PDF of (a) and , (b) and and (c) and for box-filtered DNS with Δi = 0.01δ (○), 0.02δ (∇) and 0.03δ (◇) at Reτ ≈ 950. For each probability distribution the contours are 50 % and 95 %. The straight-dashed lines are obtained by the least-squares fitting to the joint PDF. (d) The l1 dependence on Reτ with Δ2 = 0.05δ (black, bottom) and Δ2 = 0.1δ (blue, top) calculated from box-filtered DNS channel flow data (○), and estimation from box-filtered logarithmic layer approximation l1/δ = Δ2/(2δ)[log(ReτΔ2/(2δ)) − 1] + κBΔ2/(2δ) with κ = 0.41 and B = 5.3 (dashed line).
Finally, figure 3(d) shows the streamwise slip length l1 as a function of Reynolds number for a constant Δi/δ. The slip length was computed as the average ratio of and . The plot shows that the dependence of the streamwise slip length on Reynolds number is stronger for smaller Reτ. This behaviour can be explained by the relative thickness of the filter size and the buffer layer. When the ratio is of O(1), the filtered velocity at the wall takes into account contributions from the buffer layer, and l1 is expected to be sensitive to changes in Reynolds number. However, when the buffer layer is a small fraction of the filter size, most of the contribution to l1 comes from the logarithmic layer, which has a universal behaviour with Reτ. Neglecting the effect of the buffer layer, the approximate functional dependence of the slip length on Reynolds number can be estimated from the logarithmic velocity profile,
| (2.10) |
where 〈·〉 denotes ensemble average in the homogeneous directions and time, k is the von Kármán constant and B is the intercept constant. In the limit of high Reynolds numbers, the box-filtered streamwise velocity and its wall-normal derivative can be estimated by assuming a logarithmic law in the entire near-wall region and integrating (2.10). This gives an approximation for the average streamwise slip length:
| (2.11) |
(dashed lines in figure 3d), which predicts a weak Reτ dependence for large Reynolds numbers. It is important to remark that l1 from the figure is only an estimation from a priori testing and the particular values are not expected to work in an actual LES, although we expect the trends to be relevant.
2.3. Consistency constraints on the slip parameters
In an actual LES implementation, the choice of li and vi must comply with the symmetries of the flow. Moreover, it is also necessary to satisfy on average the impermeability constraint of the wall to preserve the physics of the flow (more details are offered in § 3.6). Therefore, the slip boundary condition for a plane channel flow should fulfil
| (2.12) |
Equation (2.12) can be further simplified by assuming li and vi to be constant in the homogeneous directions. Since and for i = 2, 3, 〈v2〉 and 〈v3〉 must be set to zero. We can also set 〈v1〉 = 0 without loss of generality, since its average effect can be absorbed by moving the frame of reference at constant uniform velocity. Then, the slip boundary condition consistent with the symmetries of the channel is of the form
| (2.13) |
When the flow is no longer homogeneous in x1, as in a spatially developing flat-plate boundary layer, the above arguments based on the symmetry of the channel do not hold. Then, the slip velocity vi can be used to impose zero mean mass flow through the walls and ensure that the boundary behaves, on average, as a non-permeable wall. Since the mass flow through a flat wall is only affected by v2, we can still set v1 and v3 to zero for simplicity.
3. Effect of the slip boundary condition on one-point statistics
It was argued in § 2 that the most general form of the Robin boundary condition, given by (2.1), should replace the no-slip condition in wall-modelled LES. In this section, we investigate the effects of li and vi on the one-point statistics of LES of plane turbulent channel flow and a flat-plate boundary layer. Our conclusions will be numerically corroborated by considering li and vi as free parameters in an LES with slip boundary condition at the wall. A dynamic procedure to compute these parameters is given in § 4.
3.1. Numerical experiments
We perform a set of plane turbulent channel LES listed in table 1. The simulations are computed with a staggered second-order finite difference (Orlandi 2000) and a fractional-step method (Kim & Moin 1985) with a third-order Runge-Kutta time-advancing scheme (Wray 1990). The code has been validated in previous studies in turbulent channel flows (Lozano-Durán & Bae 2016; Bae et al. 2018) and flat-plate boundary layers (Lozano-Durán, Hack & Moin 2018). The size of the channel is 2πδ × 2δ × πδ in the streamwise, wall-normal and spanwise directions, respectively. It has been shown that this domain size is sufficient to accurately predict one-point statistics for Reτ up to 4200 (Lozano-Durán & Jiménez 2014a). Periodic boundary conditions are imposed in the streamwise and spanwise directions. The eddy viscosity vt is computed at the cell centres and the values at the wall are obtained by assuming Neumann boundary conditions for the discretised vt, which is motivated by the fact that for coarse grid resolutions the SGS contribution at the wall must be non-zero. The channel flow is driven by imposing a constant mean pressure gradient, and all simulations were run for at least 100 eddy turnover times, defined as δ/uτ, after transients.
Table 1.
List of cases. The numerical experiments are labelled following the convention [SGS model]-[Reτ](-[other cases]). SGS models used are the dynamic Smagorinsky model (DSM), constant coefficient Smagorinsky model (SM), anisotropic minimum-dissipation model (AMD) and no model (NM). Grid resolutions different from the baseline case are denoted by c1 and c2. Three additional cases with different slip length than the baseline case are labelled s1, s2 and s3. See the text for details.
| Case | SGS model | Reτ | Δi/δ | l1/δ | l2/δ | |
|---|---|---|---|---|---|---|
| DSM-2000 | DSM | 2003 | 100 | 0.050 | 0.008 | 0.008 |
| DSM-2000-s1 | DSM | 2003 | 100 | 0.050 | 0.008 | 0.004 |
| DSM-2000-s2 | DSM | 2003 | 100 | 0.050 | 0.004 | 0.008 |
| DSM-2000-s3 | DSM | 2003 | 100 | 0.050 | 0.097 | 0.045 |
| DSM-2000-c1 | DSM | 2003 | 154 | 0.077 | 0.008 | 0.008 |
| DSM-2000-c2 | DSM | 2003 | 200 | 0.100 | 0.008 | 0.008 |
| DSM-950 | DSM | 934 | 46 | 0.050 | 0.008 | 0.008 |
| DSM-4200 | DSM | 4179 | 210 | 0.050 | 0.008 | 0.008 |
| AMD-2000 | AMD | 2003 | 100 | 0.050 | 0.008 | 0.008 |
| SM-2000 | SM | 2003 | 100 | 0.050 | 0.008 | 0.008 |
| NM-2000 | NM | 2003 | 100 | 0.050 | 0.008 | 0.008 |
The slip boundary condition from (2.13) is used on the top and bottom walls. We have tested the variability of li in time by oscillating li(t) with different amplitudes and frequencies around a given mean. The frequency of the oscillation considered were 0.5, 1 and 2 times the natural frequency given by the size of the grid and uτ, and the amplitudes imposed were up to 0.5 times the value of the mean. The different cases resulted in almost identical one-point statistics as those obtained with a constant li of the same mean with the relative difference in the resulting wall stress less than 0.5 % for all cases. Thus, li will be fixed to a constant value in both homogeneous directions and time for the remainder of the section.
We take as a baseline case the friction Reynolds number Reτ ≈ 2000 with a uniform grid resolution of 128 × 40 × 64 in the x1, x2 and x3 directions, respectively. The grid size in outer units is 0.050δ in the three directions, and follows the recommendations by Chapman (1979) for resolving the large eddies in the outer portion of the boundary layer. The baseline SGS model used is the dynamic Smagorinsky model (DSM) (see Germano et al. 1991; Lilly 1992). The baseline slip lengths are li = 0.008δ, i = 1, 2, 3 for reasons given in § 3.2. Three additional cases with different slip lengths, which are given in the first group of table 1, are used to study the effect of li on the one-point statistics.
To study the effects of slip boundary condition on grid resolution, we define two meshes with 82 × 26 × 42 and 64 × 20 × 32 grid points distributed uniformly in each direction, which correspond to a uniform grid size of 0.077δ and 0.100δ, respectively as listed in the second group of table 1. The resolutions were chosen such that the first interior point lies in the logarithmic region and is far from the inner-wall peak of the streamwise r.m.s. velocity. The intention is to avoid capturing (even partially) the dynamic cycle in the buffer layer, since the wall-normal lengths of the near-wall vortices and streaks scale in viscous units, and that scaling is incompatible with the computational efficiency pursued in wall-modelled LES. The range of grid resolutions is limited due to the fact that the outer layer still needs to be resolved by the LES. However, it will be shown in § 3.5 that the selected range of grid resolutions is sufficient to show the sensitivity of the slip lengths to the grid resolution.
To investigate the effect of the Reynolds number, we consider three cases DSM-950, DSM-2000 and DSM-4200, which constitute the third group of table 1. The sensitivity to the SGS model will be assessed by comparing results from DSM, constant-coefficient Smagorinsky model (SM) (see Smagorinsky 1963) without a damping function at the wall, the anisotropic minimum-dissipation model (AMD) (see Rozema et al. 2015) and cases without an SGS model (NM), given in the fourth group of table 1. Finally, LES results will be compared with DNS data from Del Alamo et al. (2004), Hoyas & Jiménez (2006) and Lozano-Durán & Jiménez (2014a).
3.2. Control of the wall stress and optimal slip lengths
In an LES of channel flow with the slip boundary condition (2.13), the wall stress is given by
| (3.1) |
where τw is the stress at the wall, is the tangential SGS stress tensor and is the result of the non-zero velocity provided by the slip condition. The slip lengths can be explicitly introduced by substituting from (2.13) such that
| (3.2) |
where may also depend on the slip lengths. Therefore, the wall stress (and hence the mass flow) can be controlled by the proper choice of slip lengths. This is an important property of the slip boundary condition, and it is illustrated in figure 4. For coarse LES with no-slip boundary conditions, the near-wall region cannot be accurately computed owing to the inadequacy of the current SGS models and large numerical errors in the near-wall region, even if the resolution is sufficient to resolve the outer layer eddies. This mainly results in under- or over-predictions of the wall stress, among other effects, and the shift of mean velocity with respect to DNS. Figure 4 shows the mean streamwise velocity profile for cases DSM-2000 and DSM-2000-s[1–3]. The results reveal that increasing l1 (at constant l2) moves up the mean velocity profile by 8%, while increasing l2 (at constant l1) have the opposite effect and decreases the mean by 15 %. Although not shown, it was tested that varying l3 has a second-order effect on the mean velocity profile when compared to changes of the same order in l1 and l2. For instance, the change in mean velocity profile is 1.2% when l3 is changed from 0.008δ to 0.004δ for case DSM-2000. The result is not totally unexpected since and are active components of the mean streamwise momentum balance in a channel flow (see (3.2)), while enters only indirectly. All calculations in the present study have been performed with l3 equal to l1.
Figure 4.
Mean streamwise velocity profile as a function of (a) outer units and (b) wall units for DSM-2000 (l1, l2) = (0.008δ,0.008δ), ○; DSM-2000-s1 (l1, l2) = (0.008δ, 0.004δ), ∇; DSM-2000-s2 (l1, l2) = (0.004δ, 0.008δ), □; DSM-2000-s3 (l1, l2) = (0.097δ, 0.045δ), ×; and DNS (dashed line).
The observations in figure 4 may be explained in terms of the mean streamwise momentum balance at the wall and non-zero streamwise slip. With respect to the former, increasing l2 enhances the contribution at the wall, which is translated into a lower mean velocity profile due to the higher momentum drain at the boundaries. The same argument applies when increasing l1. However, higher l1 also implies larger slip in x1, which overcomes the previous momentum drain, and the resulting net effect is an increase of the mean mass flow. For the laminar Poiseuille flow with the slip boundary condition, the shift in the mean velocity profile can be computed analytically and is shown to be proportional to l1.
The duality between the streamwise and wall-normal slip lengths makes it possible to always achieve the correct wall stress by an appropriate selection of (l1, l2), which we define as optimal slip lengths. The optimal slip lengths are effectively computed by running an LES with slip boundary condition using (3.2) with as a constraint, and then averaging in time the values obtained for l1 and l2. Note that we have the freedom to impose the ratio l1/l2, and the optimal slip lengths are not unique. Two examples are shown in figure 4. It is also important to remark that the control of the mean velocity profile is not possible in general without wall-normal transpiration. In particular, if an LES with l1/δ = l2/δ = 0 (no-slip) already over-predicts the mean velocity profile with respect to DNS, the only possible outcome of increasing l1/δ while maintaining l2/δ = 0 is a positive shift of the mean velocity profile. Since our experience shows that negative values of l1 will result in an unstable solution, the conclusion is that the correct mean velocity profile cannot be achieved in this case unless l2 ≠ 0, making the wall-normal slip length indispensable.
3.3. Prediction of the logarithmic layer
A second observation from figure 4 is that the shape of the mean velocity profile remains roughly constant for different slip lengths, and changes in l1 and l2 are mainly responsible for a shift along the mean velocity axis. We would like to connect the previous observation with the classic logarithmic profile for the mean streamwise velocity given in (2.10). Assuming that the filter operation does not alter the logarithmic shape of for the typical filter sizes (or grid resolutions), (2.10) should also hold for LES. However, it is not clear whether this would be the case for an actual LES. For example, Millikan’s asymptotic matching argument (Millikan 1938) requires a scale separation that tends to infinity as the Reynolds number increases, which is not the case in wall-modelled LES as the length scales are fixed in outer units. Other arguments, such as the Prandtl’s mixing length hypothesis (Prandtl 1925) would suggest that the correct wall-normal mixing of the flow should be obtained in order to recover the logarithmic profile. Alternatively, from the point of view of Townsend’s attached eddy hypothesis (Townsend 1980), the flow from the LES should be populated by a self-similar hierarchy of eddies with sizes proportional to the wall distance and the proper number of eddies per unit area. In all cases, the SGS model plays a non-negligible role in fulfilling these conditions, especially at high Reynolds numbers and coarse grids. As a consequence, not all SGS models are expected to recover the correct shape of the mean velocity profile, and this is further discussed in § 3.5.
The prominent role of the SGS model in the correct representation of the logarithmic layer can be seen from the integrated mean streamwise momentum balance for filtered velocities
| (3.3) |
By comparing the structure of (2.10) and (3.3), it is reasonable to hypothesise that the slip boundary condition mainly influences the intercept B, which is independent of x2, while the SGS model controls the x2-dependent slope 1/κ, related to the wall-normal mixing of the flow by the attached eddies. Note that this is not strictly the case, and some coupling is expected between all terms in (3.3). For example, the value of the integrand at the wall will depend on the slip lengths.
3.4. Turbulence intensities and Reynolds stress contribution
The sensitivity of to the choice of slip lengths is examined in figure 5(a). Three cases DSM-2000, DSM-2000-s1 and DSM-2000-s3 are considered, two of them supplying the correct mean velocity profile. The r.m.s. velocities are insensitive, especially away from the wall, even when the slip lengths are such that the mean velocity profile does not match that of DNS. The most noticeable difference is observed at the wall, where larger l1 results in smaller r.m.s. values. The consequence is that even if the mean velocity profile matches that of DNS for an optimal (l1, l2), some pairs are preferred in order to avoid the near-wall under- and over-shoot in the r.m.s. velocity fluctuations. A more comprehensive study of the near-wall turbulent intensities with the slip boundary condition can be found in Bae et al. (2018).
Figure 5.
(a) Streamwise, spanwise and wall-normal r.m.s. velocity fluctuations (from top to bottom), and (b) mean Reynolds stress contribution for DSM-2000 (l1, l2) = (0.008δ, 0.008δ), ○; DSM-2000-s1 (l1, l2) = (0.008δ, 0.004δ), ∇; DSM-2000-s3 (l1, l2) = (0.097δ, 0.045δ), ×; and DNS (dashed line).
Figure 5(b) stresses another important property of the slip condition. As was the case for r.m.s. velocities, the changes in the mean tangential Reynolds stresses are negligible to varying values of l1 and l2, except at the walls. For the case with larger l1, the wall-stress contribution from the is roughly 50%, and the remaining stress is then carried by the SGS and viscous terms. This can be considered an advantage compared to the classic no-transpiration condition since the SGS model, usually known to under-predict the wall stress (Jiménez & Moser 2000), is not constrained to account for the resolved non-zero at the wall.
Finally, the structure of the streamwise velocity at the wall for filtered DNS and wall-modelled LES is shown in figure 6. The filtered DNS data was obtained by box-filtering the streamwise velocity with filter size Δi = 0.050δ, i = 1, 2, 3, that coincides with the LES grid resolution. Although our analysis is qualitative, the figures show that despite the comparable intensities, the filtered DNS is organised into more elongated streaks. Also note that for a constant l1, the slip boundary condition forces the velocity and its wall-normal derivative to have the same structure close to the wall that is inconsistent with box-filtered DNS. This suggests that an accurate representation of the flow structure at the wall is neither expected nor necessary in order to obtain accurate predictions of the low-order flow statistics far from the wall. This is consistent with previous studies indicating that the outer layer dynamics are relatively independent of the near-wall cycle (Del Álamo et al. 2006; Flores & Jiménez 2006; Jiménez 2013; Mizuno & Jiménez 2013; Lozano-Durán & Jiménez 2014b; Dong et al. 2017).
Figure 6.
(Colour online) Instantaneous snapshot of the streamwise velocity at the wall for (a) box-filtered DNS (Reτ ≈ 2000), and (b) wall-modelled LES (DSM-2000) of channel flow for the x1 − x3 plane. For both cases, the filter or grid size is Δi/δ = 0.050, i = 1, 2, 3. Colours indicates velocity in wall units.
3.5. Sensitivity to SGS model, Reynolds number and grid resolution
In this section, we study the effect of the SGS model, Reynolds number and grid resolution on the mean velocity profile for the slip boundary condition. The discussion is necessary for understanding the most relevant sensitivities of wall models based on the slip boundary condition.
Figure 7 shows the sensitivity of the mean velocity to different SGS models for DSM-2000, SM-2000, AMD-2000 and NM-2000. In all of the cases, the slip lengths are fixed and equal to 0.008δ such that the velocity profile at the centre of the channel for DSM-2000 matches the DNS data. Note that this particular choice is arbitrary, and that alternative values of slip lengths could be selected to find the best match between SM-2000, AMD-2000 or NM-2000 and DNS. However, the results below are independent of this choice, since the relative shift between cases is barely affected. The results in figure 7 reveal that not only the shape but also the mean mass flow, and thus the optimal slip lengths for each SGS model, are impacted by the SGS model at grid resolutions typical of wall-modelled LES. Regarding the shape of (figure 7b), for low-dissipation SGS models (e.g. NM), the flow becomes more turbulent, causing the mean velocity profile to flatten due to the enhanced mixing. On the other hand, for highly dissipative SGS models (e.g. SM), the shape approaches a parabolic profile, that is closer to the laminar solution.
Figure 7.
(a) Effect of SGS models on the mean velocity profile for li = 0.008δ. (b) The mean velocity profiles have been shifted to compare the shapes of the mean velocity profile, where the shift is given by . Dynamic Smagorinsky model (○), constant coefficient Smagorinsky model (□), anisotropic minimum-dissipation model (◇) and no model (∇) are given for the turbulent channel with Reτ ≈ 2000. DNS (dashed line).
The effect of each SGS model on the mass flow rate in wall units can be understood by considering the definition of the friction velocity,
| (3.4) |
For a channel flow driven by a constant mass flow rate, the last term in (3.4) is zero for LES without an SGS model, which results in lower uτ and therefore a positive shift of the mean velocity profile scaled in wall units. For non-zero eddy viscosity, the mean SGS stress at the wall will contribute to increase uτ, creating a negative shift in the mean velocity profile in wall units. The actual impact of the SGS model on uτ is more intricate owing to the coupling between vt and the flow velocities. However, the qualitative behaviour of uτ described above still holds.
Conversely, the effects on the mean velocity profile can also be explained for a channel flow driven by a constant pressure gradient. In this case, the left-hand side of (3.4) is fixed. Hence, variations in the SGS stress at the wall must be compensated by variations in the Reynolds and viscous stress terms. We have observed that these changes are balanced by the viscous stress, , rather than by the Reynolds stress term. The variation in the mass flow can then be understood through the slip boundary condition, where larger implies a larger slip at the wall and, hence, higher mass flow.
Figure 8(a) shows the eddy viscosity as a function of wall-normal height for various SGS models. In particular, the eddy viscosity of DSM and AMD model are comparable far from the wall, consistent with the shape of the mean velocity profile in the outer region shown in figure 7(b). However, vt differs notably for DSM and AMD model in the first two grid points off the wall, leading to the differences in mean velocity profile observed in figure 7(a). Hence, the results above are indicative of the fact that different SGS models demand different optimal slip lengths.
Figure 8.
Eddy viscosity, vt, as a function of wall-normal height with li = 0.008δ for: (a) DSM-2000 (○) and AMD-2000 (∇); and (b) DSM-2000 (○), DSM-4200 (∇) and DMS-2000-c2 (□).
The grid resolution and Reynolds number sensitivity are studied in figure 9, again maintaining constant slip lengths. Regarding the resolution, coarsening the grid increases the mass flow. This phenomenon is also observed in LES with no-slip boundary condition and, in the present case, is probably related to an inconsistency between the choice of slip lengths and the wall-normal momentum flux provided by the SGS model. Figure 9(b) shows a weak dependence of the mean velocity profile on the Reynolds number. The most notable observation is the under-estimation of the mass flow for the lowest Reynolds number, but overall the optimal slip lengths are quite insensitive to Reτ, consistent with our analysis in § 2.2 regarding the effect of Reτ. Finally, increasing the Reynolds number or coarsening the grid resolution augments the eddy viscosity for DSM (figure 8b), which is consistent with the expected behaviour from SGS models.
Figure 9.
Effect of (a) the grid resolution and (b) Reynolds number on the mean velocity profile for li = 0.008δ: (a) Δi/δ = 0.050 (○), 0.077 (∇), and 0.100 (□); (b) Reτ ≈ 950 (∇), Reτ ≈ 2000 (○), Reτ ≈ 4200, (□). DNS (dashed line).
3.6. The role of slip velocity in imposing zero mean mass flow through the walls
As discussed in § 2.3, we require the slip velocities to guarantee no net mass flow through the walls for flows that are inhomogeneous in the wall-parallel direction. The requirement is demonstrated here in an LES of a zero-pressure-gradient flat-plate turbulent boundary layer.
The numerical method is similar to that of the channel flow presented in § 3.1 with the exception of the boundary conditions and the Poisson solver, which was modified to take into account the non-periodic boundary conditions in the streamwise direction. The simulation ranges from Reθ ≈ 1000 to 10000, where Reθ is the Reynolds number based on the momentum thickness. This range is comparable to the boundary layer simulation by Sillero, Jimenez & Moser (2013) that will be used for comparisons.
The slip boundary condition from (2.1) is used at the wall, located at x2 = 0. In the top plane, we impose u1 = U∞ (free-stream velocity), u3 = 0 and u2 estimated from the known experimental growth of the displacement thickness for the corresponding range of Reynolds numbers as in Jiménez et al. (2010). This controls the average streamwise pressure gradient, whose nominal value is set to zero. The turbulent inflow is generated by the recycling scheme of Lund, Wu & Squires (1998), in which the velocities from a reference downstream plane, xref, are used to synthesise the incoming turbulence. The reference plane is located well beyond the end of the inflow region to avoid spurious feedback (Nikitin 2007; Simens et al. 2009). In our case, xref/θ0 = 890, where θ0 is the momentum thickness at the inlet. A convective boundary condition is applied at the outlet with convective velocity U∞ (Pauley, Moin & Reynolds 1990) and small corrections to enforce global mass conservation (Simens et al. 2009). The spanwise direction is periodic. The length, height and width of the simulated box are Lx = 1060θavg, Ly = 18θavg and Lz = 35θavg, where θavg ≈ 2.12θ0 denotes the momentum thickness averaged along the streamwise coordinate. This domain size is similar to those used in previous studies (Jiménez et al. 2010; Schlatter & Örlü 2010; Sillero et al. 2013). The streamwise and spanwise resolutions are Δ1/δ = 0.05 and Δ3/δ = 0.04 at Reθ ≈ 6500. The number of wall-normal grid points per boundary layer thickness is chosen to be ~20 at the inlet, which is in line with the channel flow simulations in the previous sections. The grid is slightly stretched in the wall-normal direction with minimum Δ2/δ = 0.01 . All computations were run with CFL = 0.5 and for 50 washouts after transients.
The slip lengths are computed to match the empirical friction coefficient, Cf, from White & Corfield (2006). The connection between the slip parameters and the friction coefficient is
| (3.5) |
which is equivalent to (3.1) with the slip boundary condition applied to the u1u2 term. The slip lengths are now a function of the streamwise coordinate to take into account the inhomogeneity of the flow in x1. To ensure numerical stability, exponential filtering in time with filter size 0.2δ/uτ was applied to the slip lengths in addition to averaging in the homogeneous direction. Equation (3.5) is key to guaranteeing the correct wall stress, but we have the freedom to impose two more conditions to fully determine l1, l2 and l3. For simplicity, we set l1 = l2 = l3 = l, and compute l from (3.5) with the correct Cf prescribed. The value of v2 is computed at each time step to ensure global zero mean mass flow through the wall such that
| (3.6) |
where Δt is the time step and 〈·〉w denotes average over the entire wall. The average v2 obtained is of the order of 10−3U∞. The slip velocities v1 and v3 in (2.1) are set to zero.
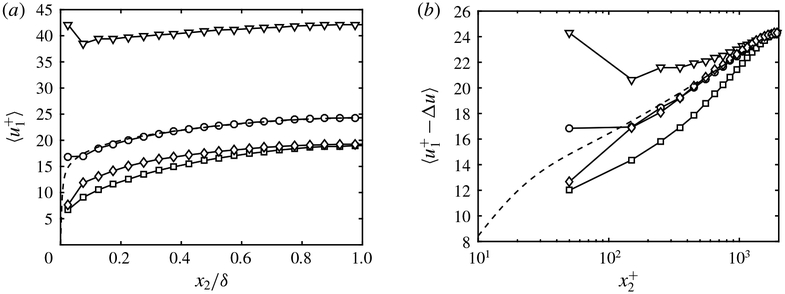
Figure 10(a) shows the resulting mean slip lengths computed to produce the target Cf, which is successfully achieved as shown in figure 10(b). It is important to stress again that one of the main differences of the boundary layer case with respect to the channel flow is the necessity of a non-zero v2 term from (2.1) to guarantee that the wall behaves as a no-transpiration boundary on average. We have implemented a global condition (constant-in-space v2, equation (3.6)) that does not prevent instantaneous local mass flow at a particular streamwise location as seen in figure 10(c). However, the mean mass flow remains locally close to zero for all streamwise locations.
Figure 10.
(Colour online) (a) Mean slip lengths l normalised by θavg, the average momentum thickness, (b) the friction coefficient from the LES with slip boundary condition (black —) and the empirical friction coefficient from White & Corfield (2006) (red ○), and (c) the instantaneous (black solid line) and time-averaged (red dashed line) wall-normal velocities at the wall as a function of Reθ.
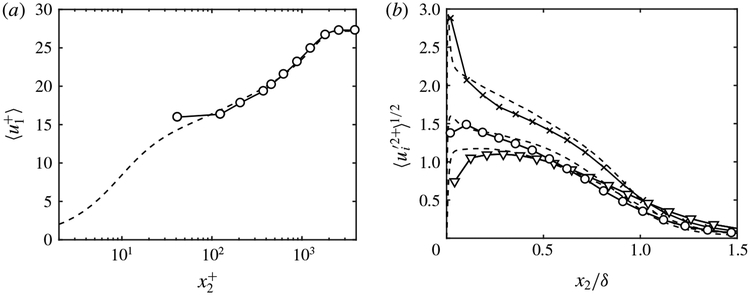
The mean streamwise velocity and the three r.m.s. velocity fluctuations at Reθ ≈ 6500 (Reτ ≈ 1989.5) are shown in figure 11 and compared with Sillero et al. (2013). As expected, the mean DNS and LES velocities match in the wake region, as the correct Cf in the LES is imposed. The shape of the profile is also well predicted. The r.m.s. velocities are reasonably well reproduced at this Reynolds number, with no over-prediction of the streamwise r.m.s. velocity and under-prediction of the other two components close to the wall, consistent with the analysis in § 3.4. Overall, these results along with those from LES of channel flow in the previous sections show that the slip boundary condition successfully reproduces the one-point statistics of the flow as long as the slip lengths accurately reflect the correct mean wall stress.
Figure 11.
(a) Mean streamwise velocity profile and (b) r.m.s. streamwise (×), spanwise (○) and wall-normal (∇) fluctuation profiles at Reτ ≈ 6500. Symbols are for LES. DNS from Sillero et al. (2013) (dashed line).
Two more cases (not shown) were run to test the effect of the slip boundary condition on the net mass flow through the wall. In the first case, a slip boundary condition was imposed such that the net mass flow through the wall is positive (incoming flow through the wall) such that . In this case, the boundary layer thickness grew five times faster than the reference DNS. In contrast, when the simulation was run with net negative mass flow through the walls ., the flow remained laminar. The results are consistent with observations in previous studies on blowing and suction of boundary layers (Simpson, Moffat & Kays 1969; Antonia et al. 1988; Chung & Sung 2001; Yoshioka & Alfredsson 2006) and highlight the relevance of imposing a correct zero net mass flow through the walls to faithfully predict the boundary layer growth.
4. Dynamic wall models for the slip boundary condition
It is pertinent to discuss first the expected role of wall models in LES. From § 3.3 and previous analysis in the literature (Lee, Cho & Choi 2013), the most important requirement for a wall model is to supply accurate mean tangential stress at the wall. This requirement must be accompanied by an effective SGS model responsible for generating correct turbulence statistics in the outer region, where the wall model plays a secondary role. The first requirement is necessary for obtaining the correct bulk velocity, whereas the last point is crucial to predict the shape of the mean velocity profile and r.m.s. velocity fluctuations far from the wall (see §§ 3.2 and 3.4).
The wall models reviewed in the introduction are capable of meeting the first requirement by assuming a specific state of the boundary layer and relying on empirical parameters consistent with such state. In this regard, most traditional wall models assume quasi-equilibrium turbulence in the vicinity of the wall and encode explicitly or implicitly information about the law of the wall, which cannot be derived from first principles but can only be extracted from DNS or wind tunnel experiments, such as the values of κ and B. Despite the equilibrium-turbulence assumption, current wall-modelling approaches have been successful in predicting numerous flow configurations up to date, although their performance in some regimes such as transitional or separated flows as well as non-equilibrium turbulence is still open to debate.
The main purpose of a dynamic wall model is similar to that of traditional wall models, i.e. the estimation of accurate wall stress τw. However, the objective is to achieve this goal without prior assumptions regarding the state of the boundary layer or embedded empirical parameters. Instead, dynamic wall models aim to use only the current (local) state of the LES velocity field and universal modelling assumptions valid across different flow scenarios. Note that the task outlined above is an outstanding challenge, since without any empirical coefficients there is no explicit reference to how the near-wall flow should behave in different situations. Moreover, the instantaneous velocity field is intertwined with the effects of the LES grid resolution, Reynolds number and SGS model choice as documented in previous sections. In addition, numerical errors are amplified at the wall, and discretisation schemes are expected to play an important role as well. Dynamic models must encompass these factors to be of practical use, and whether this can be accomplished for arbitrary flow configurations remains to be demonstrated.
Despite the aforementioned difficulties, we provide below a dynamic slip wall model that shows the ability to adapt to different grid resolutions and Reynolds numbers as well as flow configurations, provided an SGS model. For a slip boundary condition of the form (2.1), the problem of estimating τw can be reformulated as finding the value of slip parameters that provides the correct mean wall stress. The relationship between l and τw was shown in §§ 3.2 and 3.6 for channels and boundary layers. Moreover, for the slip boundary condition to be used as a predictive tool in wall-modelled LES, the computed li and vi should comply with the observations discussed in the previous sections.
4.1. Previous dynamic models
Bose & Moin (2014) introduced a dynamic wall model based on the slip boundary condition free of any a priori parameters. The slip length, assumed to be equal for the three spatial directions, is computed via a modified form of the Germano’s identity (Germano et al. 1991),
| (4.1) |
where l is the slip length, is the test filter, ΔR is the filter size ratio between the test and grid filters, and represent the grid and test filter SGS tensors, respectively. Equation (4.1) is then solved for l by using least squares.
In Bose & Moin (2014), the model was tested for a series of LES of turbulent channel flow and NACA 4412 airfoil. However, our attempts to reproduce the channel flow results did not perform as expected with our current implementation, which uses a different SGS model and numerical discretisation. The discrepancies motivated a deeper study of the slip boundary condition and investigation of alternative dynamic wall models as that presented in the next section.
4.2. Wall-stress invariant dynamic wall model
We present a dynamic wall model formulated for the slip boundary condition based on the invariance of wall stress under test filtering. We will refer to this new model as the wall-stress invariant model (WSIM). We will assume a single slip length l1 = l2 = l3 = l and neglect any potential contribution from the terms vi. The goal is to define a dynamic procedure to obtain l at each time step such that the mean wall stress obtained from (3.1) is an accurate representation of the stress resulting from solving the Navier–Stokes equations with DNS resolution.
Let us consider the wall-stress operator given by
| (4.2) |
where terms Rij, , Sij and pδij are the Reynolds stress, subgrid stress, strain-rate and pressure tensors, respectively, computed from the specified velocity field u. In our formulation of the wall is assumed to be smooth, but the wall stress can be extended to encode information about the type of wall (smooth, rough, hydrophobic, etc.) by adding the appropriate drag terms into the right-hand side of (4.2).
The modelling choice for the dynamic wall model is
| (4.3) |
| (4.4) |
where the different wall stresses, , are obtained by either computing the stress of the filtered velocity field or by filtering the total stress. Condition (4.3) enforces the invariance of wall stress under test filtering and allows the wall model to predict the same wall stress regardless of the grid resolution (or filter). A similar approach was also adopted by Anderson & Meneveau (2011) for rough walls. Condition (4.4) is analogous to the Germano’s identity for the total stress of the filtered velocity and can be interpreted as a consistency condition between the wall stress and filter operator. The proposed model is given by combining (4.3) and (4.4) such that
| (4.5) |
The rationale for this particular combination of (4.3) and (4.4) is given by considering , the dominant shear stress component in a boundary layer. This term can be simplified by test filtering only in the wall-normal direction with a box filter with filter size at . Assuming that the subgrid stress tensor is given by an eddy viscosity, i.e. and that vt is constant in the near-wall region, the first-order approximation of can be shown to be
| (4.6) |
Hence, implicitly enforces the well-established constant stress layer across the wall-normal direction. Note that (4.3) and (4.4) may be combined differently to produce alternative versions of (4.5), but not all these groupings lead to a first-order approximation consistent with the form reported in (4.6). For example, enforcing only (4.3) would not be consistent with (4.6). Nevertheless, wall models using different variants of (4.5) may be constructed based on similar principles; a broader family of dynamic models postulated on stress-invariant principles was investigated in Lozano-Durán et al. (2017).
Next we introduce an explicit dependence on the slip length condition in (4.5). We will assume that the slip boundary condition also applies for the test-filtered velocity field,
| (4.7) |
where is the slip length at the test filter level. We further suppose that a linear functional dependence of the slip length with the filter size of the form holds. This assumption will be shown to be reasonably well satisfied in figure 13(c), which contains a posteriori values for the optimal slip length (3.2) as a function of grid resolution. Introducing the slip boundary condition at grid- and test-filter levels for the Reynolds stress terms in and , such that
| (4.8a,b) |
the WSIM becomes
| (4.9) |
which can be rewritten as
| (4.10) |
with
| (4.11a,b) |
The system (4.10) is over-determined and l is computed via least squares as
| (4.12) |
where repeated indices imply summation and the compact notation and is used. For incompressible flows, the isotropic part of is usually not defined by the SGS models and, since the system is already over-determined, we exclude the i = j components of (4.12).
Figure 13.
Error in the streamwise mean velocity profile, , as a function of (a) grid size (for Reτ ≈ 4200) and (b) Reynolds number (for grid G1). WSIM (○) and EQWM (◇). The predicted slip lengths l/δ for WSIM (solid lines) and optimal slip lengths (dashed lines) as a function of (c) grid resolution for Reτ ≈ 4200 and (d) Reynolds number for grid G1.
Note that the first part of the right-hand-side of (4.9), , is the result of applying the boundary condition at the grid and test filter levels. The remaining terms, , then act as an effective control such that the slip length increases if the current wall stress is under-predicted, and decreases if the wall stress is over-predicted. This self-regulating mechanism can be examined by analysing the terms , and for three test cases of a channel flow at Reτ ≈ 4200 with DSM and grid Δ1 = Δ2 = Δ3 = 0.05δ. The first case is computed by imposing the optimal slip length, l = lopt = 0.009δ. The second and third cases are analogous to the first case but with l = 1.70lopt and l = 0.35lopt, respectively. The terms , and were evaluated after the cases were run with their corresponding slip lengths fixed in time until the statistically steady state was reached. Note that can be interpreted as the model prior to applying the control mechanism, and this allows us to define two slip lengths, namely, and .
The terms , and evaluated from the three test cases are plotted in figure 12(a), and the corresponding slip lengths and are presented in figure 12(b). The results show that application of WSIM recovers the optimal slip length, and thus the correct wall stress, through the control mechanism . The analysis provided here is performed a priori, that is, the wall model was used to predict l at time t + Δt for a given flow field at time t, but without an actual dynamic coupling between WSIM and LES. The remainder of the paper is devoted to testing the WSIM in LES under different test scenarios.
Figure 12.
(Colour online) (a) Plots of , and computed from LES of channel flow using the slip boundary condition with fixed l equal to l = 0.35lopt = 0.003δ, l = lopt = 0.009δ, and l = 1.70lopt = 0.015δ. (b) The slip lengths , normalised by the optimal slip length. Here ΔR was assigned to be 1.6 (see § 5.1). The vertical dotted lines are l = lopt. Red arrows highlight the improvement achieved by including the control term . See the text for further details.
5. Performance of the WSIM
5.1. Numerical experiments
To test the performance of the WSIM, three flow configurations are considered: a statistically steady plane turbulent channel (2-D channel), a non-equilibrium three-dimensional transient channel (3-D channel) and a zero-pressure-gradient flat-plate turbulent boundary layer. The numerical methods of the simulations are the same as those given in §§ 3.1 and 3.6. The 2-D channel flow and the turbulent boundary layer were discussed in § 3. The three-dimensional transient channel flow is a temporally developing turbulent boundary layer in a planar channel subjected to a sudden spanwise forcing as in Moin et al. (1990).
The size of the 2-D and 3-D channel domain is 8πδ × 2δ × 3πδ in the streamwise, wall-normal and spanwise directions, respectively. For both 2-D and 3-D channel flows, periodic boundary conditions are applied in the streamwise and spanwise directions. For the top and bottom walls, we impose either the no-slip (NS), slip boundary condition for WSIM, or Neumann boundary condition for cases with the equilibrium wall model (EQWM). The formulation for the EQWM follows Kawai & Larsson (2013) with a matching location at the third grid cell for the streamwise velocity, although recent studies have shown that the first grid cell may be used for the EQWM when the velocities are filtered using a spatial or temporal filter (Yang, Park & Moin 2017) following the methodology first introduced for algebraic wall models (Bou-Zeid, Meneveau & Parlange 2004).
For the 2-D channel, the flow is driven by imposing a constant mean pressure gradient and the simulations are started from a random initial condition run for at least 100δ/uτ after transients. In the case of the 3-D channel, the calculations were started from a 2-D fully developed plane channel flow driven by a streamwise mean pressure gradient. The subsequent calculations were performed with a transverse (spanwise) mean pressure gradient of ∂P/∂x3 = 10τw0/δ, where τw0 is the mean wall shear stress of the unperturbed channel. The 3-D channel simulations were run for 10uτ0/δ and averaged over seven realisations, where uτ0 is the friction velocity of the 2-D initial condition.
For the boundary layer, the set-up is identical to that in § 3.6. The range of Reθ is from 1000 to 10000. The length, height and width of the simulated box are Lx =1060θavg, Ly = 18θavg and Lz = 35θavg with the streamwise and spanwise resolutions of Δ1/δ = 0.05 and Δ3/δ = 0.04 at Reθ ≈ 6500. The grid is slightly stretched in the wall-normal direction with minimum Δ2/δ = 0.01 . The inlet, outlet and top boundary conditions are as in § 3.6 with xref/θ0 = 890. For the wall, we impose the slip boundary condition for the WSIM.
It is important to note the details of the filter operation, as dynamic wall models are particularly sensitive to this choice (see Appendix). Test filtering a variable f in a given spatial direction at point i is computed as 1/6f (i − 1) + 2/3f (i) + 1/6f (i + 1) (Simpson’s rule). The operation is repeated for all three directions away from the wall. This corresponds to a discrete fourth-order quadrature over a cell of size 2Δ1 × 2Δ2 × 2Δ3 for a uniform grid. At the wall, the same filtering operation is used in the horizontal directions while the wall-normal filter is one-sided and given by 2/3f(1) + 1/3f(2), with f(1) and f(2) denoting values at the first and second wall-normal grid points. This is an integration over a cell of size 2Δ1 × Δ2 × 2Δ3. In addition, the definition of the filter operation fixes the value of ΔR, which is the ratio between the grid and test filter sizes at the wall. In this case, the ΔR based on the cell volume is given by .
The cases for the 2-D and 3-D channel are labelled following the convention ([Channel type]-[Wall model]-[Reynolds number]-[Grid]), where the grid labels G0, G1, and G2 given in table 2 correspond to 320 × 25 × 120 (Δ1 = Δ2 = Δ3 = 0.080δ), 512 × 40 × 192 (Δ1 = Δ2 = Δ3 = 0.050δ), and 1024 × 80 × 384 (Δ1 = Δ2 = Δ3 = 0.025δ), respectively. The wall models applied are labelled NS, EQWM or WSIM. Additional cases with anisotropic grids, different values of ΔR, test-filtering operations or SGS models were run to study the sensitivity of the model to these choices. They are discussed in the Appendix but not included in the table.
Table 2.
Grid resolutions in outer units. The first column contains the label used to name LES cases for the 2-D and 3-D channel flow simulations computed with different grids. The second, third and fourth columns are the streamwise, wall-normal and spanwise grid resolutions, respectively.
| Grid label | Δ1/δ | Δ2/δ | Δ3/δ |
|---|---|---|---|
| G0 | 0.080 | 0.080 | 0.080 |
| G1 | 0.050 | 0.050 | 0.050 |
| G2 | 0.025 | 0.025 | 0.025 |
The 2-D channel results are compared with DNS data from Hoyas & Jimenez (2006) and Lozano-Durán & Jiménez (2014a) for Reτ ≈ 2000 and 4200, Yamamoto & Tsuji (2018) for Reτ ≈ 8000 and with the law-of-the wall for Reτ > 8000. For the boundary layer, the resulting friction coefficient is compared with the empirical Cf from White & Corfield (2006), and the mean velocity profiles are compared with the DNS data from Sillero et al. (2013) at Reθ ≈ 6500 and the experimental data from Österlund (1999) at Reθ ≈ 8000.
The performance of the WSIM in laminar flows has not been studied. However, in the limit of fine grids, the dynamic procedure of WSIM should produce zero slip lengths and revert to the no-slip boundary condition. Thus, for laminar cases with enough grid resolution to resolve the near-wall structures, we expect the dynamic wall model to naturally switch off.
5.2. Statistically steady two-dimensional channel flow
We assess the performance of the WSIM compared with EQWM and NS. The results are discussed in terms of the error in the streamwise mean velocity profile across the logarithmic region. This choice was necessary to include higher-Reynolds-number cases where the corresponding DNS was not available and the law of the wall is used instead. Restricting the error to be evaluated only in the logarithmic layer is justified as wall models mainly impact the solution by vertically shifting the mean velocity profile and do not alter its shape for the range of grid resolutions tested as shown in § 3.3. In particular, the error is measured as the normalised L2 error of the streamwise mean velocity between the second grid point and 0.2δ,
| (5.1) |
In the case where the corresponding DNS does not exist, is replaced by the law of the wall,
| (5.2) |
with κ = 0.392 and B = 4.48 (Luchini 2017).
Figure 13(a,b) show as a function of grid resolution and Reynolds number. At moderate Reynolds numbers (Reτ < 8000) and all grid resolutions, the error for WSIM is similar to that of the EQWM . With increasing Reynolds number, the performance degrades , while the EQWM does not. The accurate results for EQWM are not surprising as its modelling assumptions are well satisfied for channel flow settings. The reason for the declining performance of WSIM at very high Reynolds number can be found in §§2.1 and 2.2, where it was argued that the underlying assumptions for the slip condition are invalidated for large filter sizes. However, it is worth mentioning that the errors for an LES with no wall model are an order of magnitude larger than the errors of WSIM for all cases. The mean velocity profiles and streamwise r.m.s. velocity fluctuations for WSIM for various cases are shown in figure 14. Additional sensitivities to anisotropic grids, different values of ΔR, test-filtering operations or SGS model are discussed in the Appendix.
Figure 14.
(a) Mean velocity profiles and (b) streamwise r.m.s. velocity fluctuations for WSIM at Reτ ≈ 4200 for grid G0 (∇), G1 (○) and G2 (□). DNS for Reτ ≈ 4200 (dashed line). (c) Mean velocity profiles and (d) streamwise r.m.s. velocity fluctuations for WSIM at Reτ ≈ 2000 (□), 4200 (○), 8000 (∇) and 20000 (◇) for grid G1. DNS for Reτ ≈ 4200 (dashed line).
The slip lengths predicted by the WSIM are shown in figure 13(c,d) as a function of grid resolution and Reynolds number and compared to the optimal slip lengths (3.2). It is remarkable that the WSIM captures the overall behaviour of the optimal slip lengths, that is, a strong dependence on grid resolution and a weak variation with Reynolds number.
5.3. Three-dimensional transient channel flow
The performance of WSIM in non-equilibrium scenarios is assessed in a three-dimensional transient channel flow (Moin et al. 1990). Note that in general wall models cannot be assumed to be effective at transferring information from the inner to the outer layer in non-equilibrium flows. Hence, the current flow set up, characterised by a spanwise boundary layer growing from the wall owing to viscous effects, is expected to be problematic for wall-modelled LES. A plane channel flow was modified to incorporate a lateral (transverse) pressure gradient 10 times that of the streamwise pressure gradient. The details of the simulations were given in § 5.1.
The wall models explored are the WSIM and EQWM. A case with the no-slip boundary condition is used for control, and the figure of merit is the evolution of the streamwise and spanwise wall stress as a function of time (figure 15). Note that the temporal increment of the wall stress magnitude involves an increase of the Reynolds number from Reτ ≈ 932 at t = 0 to Reτ ≈ 2600 at t = 10δ/uτ0. The results show that the performance of the WSIM is similar to the EQWM despite its parameter-free nature. The streamwise and spanwise mean velocity profiles at various time instances are given in figure 16, which also shows that both the WSIM and EQWM predict similar time evolutions. Although there is no reference DNS available for the full time span of our simulations, in the limited time range from t = 0 to 1δ/uτ0, Giometto et al. (2017) showed that the EQWM predicts the evolution of the wall stresses with less than 10 % deviation in the spanwise wall-stress prediction from DNS, and thus the results from the WSIM are also expected to exhibit a similar error. Both the EQWM and WSIM entail a quantitative correction to the prediction provide by the no-slip boundary condition. Consequently, the computational simplicity and absence of a secondary mesh makes the WSIM an appealing approach at the cost of a moderate attenuation of the predictive capabilities compared with more sophisticated wall models.
Figure 15.
Wall stress in (a) streamwise and (b) spanwise directions as a function of time for the WSIM (○), EQWM (◇) and NS (×).
Figure 16.
Mean (a) streamwise and (b) spanwise velocity profiles as a function of x2/δ at tu tuτ0/δ = 0 (solid lines), 4.5 (dashed lines) and 9 (dotted lines) for the WSIM (○) and EQWM (◇).
5.4. Zero-pressure-gradient flat-plate turbulent boundary layer
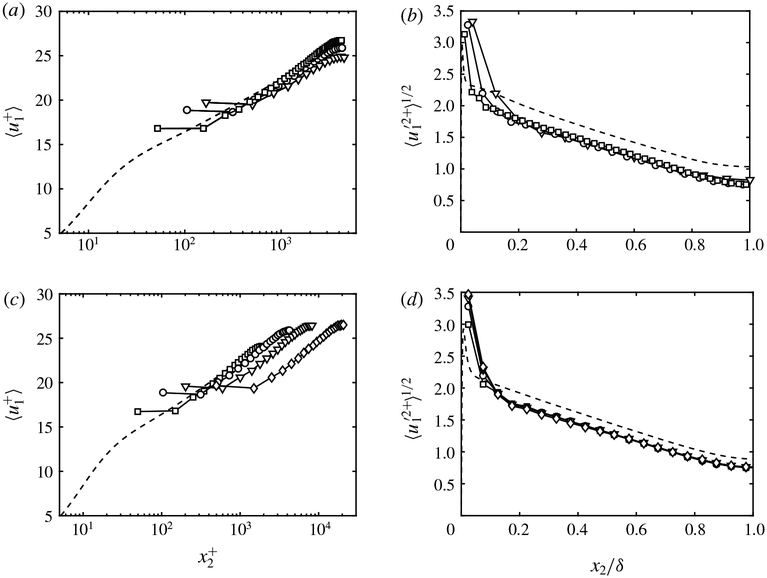
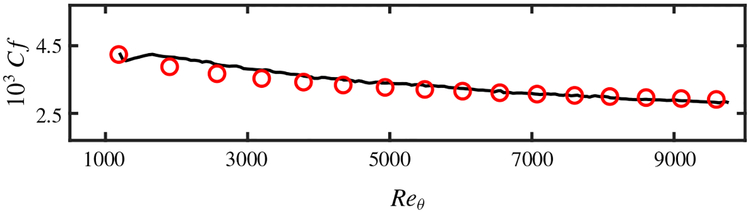
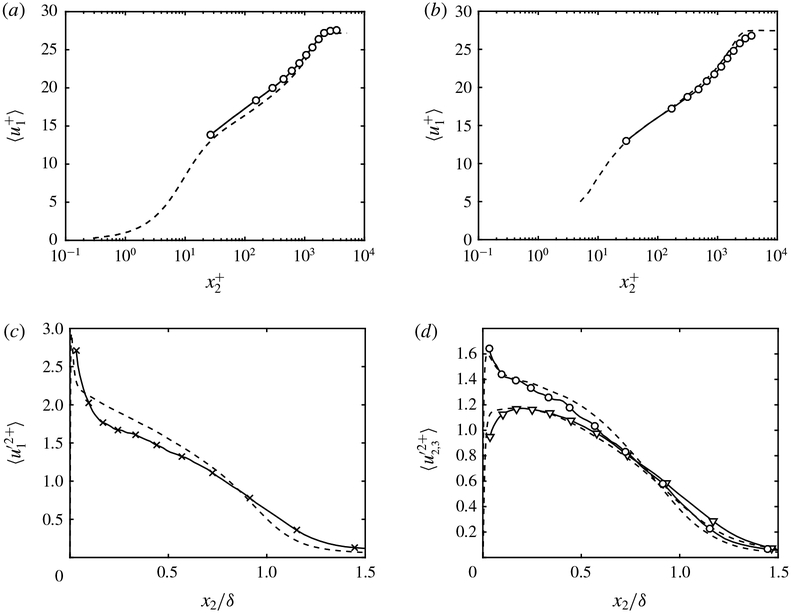
Finally, the performance of WSIM is assessed in a flat-plate turbulent boundary layer. The details of the numerical set-up were discussed in § 5.1. The friction coefficient is shown in figure 17 from Reθ ≈ 1000 to 10000. Note that the recycling scheme of Lund et al. (1998) imposes an artificial boundary condition at the inlet, requiring an initial development region for the flow to fully adapt to the slip boundary condition, which is the reason for the discrepancy in Cf near the inlet. Consistent with previous test cases, the results show that WSIM predicts the friction coefficient well within 4 % error for Reθ > 6000. The mean streamwise velocity profile at Reθ ≈ 6500 and 8000 and the r.m.s. velocity fluctuations at Reθ ≈ 6500 are also well predicted as reported in figure 18.
Figure 17.
(Colour online) Empirical friction coefficient from White & Corfield (2006) (red ○) and the friction coefficient from WSIM (black ——).
Figure 18.
Mean streamwise velocity profile for (a) Reθ ≈ 6500 and (b) Reθ ≈ 8000, and the r.m.s. (c) streamwise (×), (d) spanwise (○) and wall-normal (∇) fluctuation profiles at Reθ ≈ 6500. WSIM (symbols) and DNS (Sillero et al. 2013) or experiment (Österlund 1999) (dashed line).
6. Conclusions
Owing to the scaling of grid resolution requirements in DNS and wall-resolved LES, wall-modelled LES stands as the most viable approach for most engineering applications. In most existing wall models, the Dirichlet no-slip boundary condition at the wall is replaced by a Neumann and no-transpiration conditions in the wall-parallel and wall-normal directions, respectively. In this study, we have investigated the efficacy of the Robin (slip) boundary condition, where the velocities at the wall are characterised by the slip lengths and slip velocities. One novel aspect of this boundary condition is the non-zero instantaneous wall-normal velocity at the wall, i.e. transpiration, that opens a new avenue to model near-wall turbulence in LES. We have also presented a new dynamic slip wall model, WSIM, that is free from a priori tunable RANS parameters, which most traditional wall models for LES rely on. The model is based on the invariance of the wall stress under test filtering and is effectively applied through the slip boundary condition.
We have provided theoretical support for the use of the slip condition in wall-modelled LES instead of the widely applied Neumann boundary condition with no-transpiration. A priori testing was performed to assess the validity of the slip condition in the context of filtered DNS data.
The slip boundary condition was implemented in LES of channel flow to gain a better insight into its capabilities and shortcomings. One of the key properties, made possible by transpiration, is that the correct wall stress can always be achieved by an appropriate combination of slip lengths. This property is crucial when the grid resolution in the near-wall region does not capture the buffer and logarithmic layer dynamics, which may result in an under- or over-prediction of the wall stress. We have derived the consistency conditions for coupling the wall stress with the slip boundary condition in channel flows and flat-plate boundary layers, and showed that such constraints are sufficient to guarantee the correct wall stress. Another advantage emanates from the non-zero Reynolds stress at the wall. This is not only consistent with the filtered velocity fields, but also alleviates the well-known problem of wall-stress under-estimation by commonly used SGS models. We have also assessed the sensitivities of one-point statistics to grid refinements, changes in Reτ and different SGS models. The role of imposing zero mean mass flow through the wall by proper calculation of the slip parameters has also been shown to be a key component of the model.
Finally, we have tested the performance of a dynamic slip wall model, WSIM, in an LES of a plane turbulent channel flow at various Reynolds numbers and grid resolutions. The model was able to correctly capture the overall behaviour of the optimal slip length for a wide range of grid resolutions and Reynolds numbers. The results have been compared with those from the EQWM and the no-slip boundary condition. In all cases, WSIM performed substantially better than the no-slip, and the predictive error in the mean velocity profile was found to be less than 10 % for Reτ < 10000 and all grid resolutions investigated. The model was also tested for a LES of three-dimensional transient channel flow, where the performance was similar to that of the EQWM, and a zero-pressure-gradient flat-plate turbulent boundary layer at Reθ up to 10000, where the error in the friction coefficient was less than 4%.
The present work has established the foundations and underlying principles for using the slip boundary condition for dynamic wall-modelled LES, free of a priori tunable parameters. Based on the principles laid out in this paper, new formulations of the wall-stress-invariant condition can be explored to account for the dependency on SGS models and numerical filtering operations documented in the Appendix.
Acknowledgements
This work was supported by NASA under the Transformative Aeronautics Concepts Program, grant no. NNX15AU93A. We are grateful to K. P. Griffin for his helpful comments on the manuscript.
Appendix. Wall-stress invariant model: additional sensitivity analysis
Four additional cases were computed to analyse the sensitivity of the WSIM to ΔR, grid anisotropy, shape of the test filter and choice of SGS model. The effect of ΔR turned out to be negligible for the plausible range of values ΔR = [1.4, 1.8], and the measured difference in was less than 1 %. Regarding grid anisotropy, coarsening case 2D-WSIM-4200-G1 by a factor of two in the streamwise and spanwise directions had a negligible effect on . While coarsening in both the streamwise and spanwise directions simultaneously by a factor of two had a larger effect with increasing to ≈8 %. The error trend for anisotropic grids also follows the results shown in figure 13(a) when scaled with grid size based on cell volume, Δ = (Δ1Δ2Δ3)1/3. This shows that the wall model is robust to mild grid anisotropies.
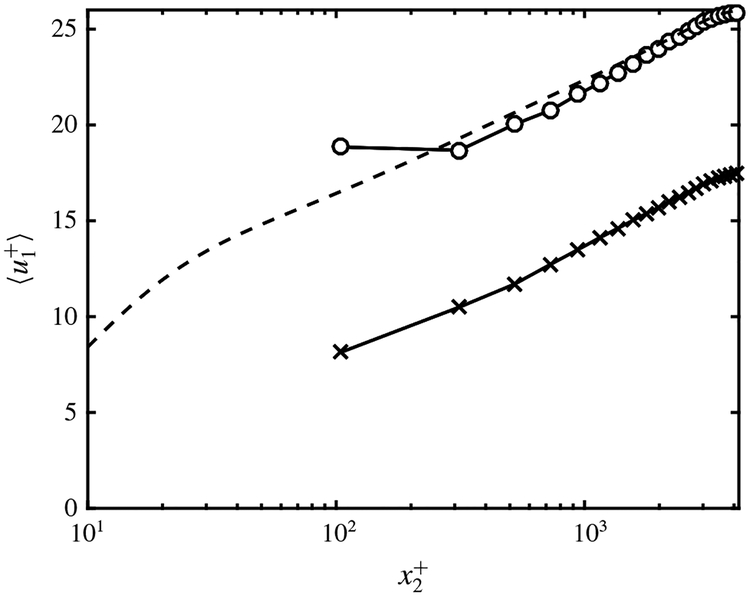
In contrast, the test filter shape and SGS model highly impacted the prediction of the mean flow. Case 2D-WSIM-4200-G1 was repeated using test filter based on the trapezoidal rule, and the error increased from 2.5% to 32% (figure 19). When 2D-WSlM-4200-G1 was run using the AMD model (Rozema et al. 2015), the stress provided by the SGS model was larger than , and the slip length prediction by WSIM was clipped to zero due to the excess of wall stress, reverting the boundary condition to no-slip. Although this is consistent with the fact that (see figure 8a), it also implies that the correct stress at the wall can never be obtained through the slip boundary condition with a single slip length in this case. It was shown in § 3 that the slip lengths in the wall-normal direction must be larger than those in the wall-parallel direction to drain the excess of stress supplied by the SGS model. This suggests that WSIM should be generalised to a formulation with a different slip length in each spatial direction to overcome this limitation. It also remains to study the near-wall behaviour of various SGS models in the wall-modelled grid limits in more detail.
Figure 19.
Mean streamwise velocity profile for the WSIM for a filter using Simpson’s rule (○) and trapezoidal rule (×). DNS (dashed line). See § 5.1 for details regarding the test filter operators.
REFERENCES
- Anderson W & Meneveau C 2011. Dynamic roughness model for large-eddy simulation of turbulent flow over multiscale, fractal-like rough surfaces. J. Fluid Mech. 679, 288–314. [Google Scholar]
- Antonia RA, Fulachier L, Krishnamoorthy LV, Benabid T & Anselmet F 1988. Influence of wall suction on the organized motion in a turbulent boundary layer. J. Fluid Mech. 190, 217–240. [Google Scholar]
- Bae HJ & Lozano-Durán A 2017. Towards exact subgrid-scale models for explicitly filtered large-eddy simulation of wall-bounded flows CTR Annu. Res. Briefs, pp. 207–214. Center for Turbulence Research. [PMC free article] [PubMed] [Google Scholar]
- Bae HJ, Lozano-Durán A, BOSE ST & MOIN P 2018. Turbulence intensities in large-eddy simulation of wall-bounded flows. Phys. Rev. Fluids 3, 014610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bae HJ, Lozano-Durán A & MOIN P 2016. Investigation of the slip boundary condition in wall-modeled LES CTR Annu. Res. Briefs, pp. 75–86. Center for Turbulence Research. [PMC free article] [PubMed] [Google Scholar]
- Balaras E, Benocci C & Piomelli U 1996. Two-layer approximate boundary conditions for large-eddy simulations. AIAA J. 34 (6), 1111–1119. [Google Scholar]
- Bose ST 2012. Explicitly filtered large-eddy simulation: with application to grid adaptation and wall modeling. PhD thesis, Stanford University. [Google Scholar]
- Bose ST & Moin P 2014. A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 26 (1), 015104. [Google Scholar]
- Bose ST & Park GI 2018. Wall-modeled LES for complex turbulent flows. Annu. Rev. Fluid Mech. 50 (1), 535–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bou-Zeid E, Meneveau C & Parlange MB 2004. Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res 40 (2), 216–227. [Google Scholar]
- Cabot WH & Moin P 2000. Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow Turbul. Combust 63, 269–291. [Google Scholar]
- Chapman DR 1979. Computational aerodynamics development and outlook. AIAA J. 17 (12), 1293–1313. [Google Scholar]
- Choi H & Moin P 2012. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24 (1), 011702. [Google Scholar]
- Chung D & Pullin DI 2009. Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631, 281–309. [Google Scholar]
- Chung YM & Sung HJ 2001. Initial relaxation of spatially evolving turbulent channel flow with blowing and suction. AIAA J. 39 (11), 2091–2099. [Google Scholar]
- Deardorff J 1970. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41 (1970), 453–480. [Google Scholar]
- Del Álamo JC, Jiménez J, Zandonade P & Moser RD 2004. Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144. [Google Scholar]
- Del Álamo JC, Jiménez J, Zandonade P & Moser RD 2006. Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358. [Google Scholar]
- Dong S, Lozano-Durán A, Sekimoto A & Jiménez J 2017. Coherent structures in homogeneous shear turbulence compared with those in channels. J. Fluid Mech. 816, 167–208. [Google Scholar]
- Flores O & Jiménez J 2006. Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376. [Google Scholar]
- Germano M, Piomelli U, Moin P & Cabot WH 1991. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760–1765. [Google Scholar]
- Ghosal S & Moin P 1995. The basic equations for the large eddy simulation of turbulent flows in complex geometry. J. Comput. Phys 118 (1), 24–37. [Google Scholar]
- Giometto BMG, Lozano-Durán A, Park GI & Moin P 2017. Three-dimensional transient channel flow at moderate Reynolds numbers: analysis and wall modeling CTR Annu. Res. Briefs, pp. 193–205. Center for Turbulence Research. [Google Scholar]
- Hoyas S & Jiménez J 2006. Scaling of the velocity fluctuations in turbulent channels up to Reτ = 2003. Phys. Fluids 18 (1), 011702. [Google Scholar]
- Jiménez J 2013. Near-wall turbulence. Phys. Fluids 25 (10), 101302. [Google Scholar]
- Jiménez J, Hoyas S, Simens MP & Mizuno Y 2010. Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360. [Google Scholar]
- Jiménez J & Moser RD 2000. Large-eddy simulations: where are we and what can we expect? AIAA J. 38 (4), 605–612. [Google Scholar]
- Kawai S & Larsson J 2013. Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers. Phys. Fluids 25 (1), 015105. [Google Scholar]
- Kim J & Moin P 1985. Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys 59, 308–323. [Google Scholar]
- Larsson J, Kawai S, Bodart J & Bermejo-Moreno I 2016. Large eddy simulation with modeled wall-stress: recent progress and future directions. Mech. Engng Rev. 3 (1), 1–23. [Google Scholar]
- Lee J, Cho M & Choi H 2013. Large eddy simulations of turbulent channel and boundary layer flows at high Reynolds number with mean wall shear stress boundary condition. Phys. Fluids 25 (11), 110808. [Google Scholar]
- Leonard A 1975. Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. Geophys 18, 237–248. [Google Scholar]
- Lilly DK 1992. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4 (3), 633–635. [Google Scholar]
- Lozano-Durán A & Bae HJ 2016. Turbulent channel with slip boundaries as a benchmark for subgrid-scale models in LES CTR Annu. Res. Briefs, pp. 97–103. Center for Turbulence Research. [PMC free article] [PubMed] [Google Scholar]
- Lozano-Durán A, BAE HJ, BOSE ST & MOIN P 2017. Dynamic wall models for the slip boundary condition CTR Annu. Res. Briefs, pp. 229–242. Center for Turbulence Research. [PMC free article] [PubMed] [Google Scholar]
- Lozano-Durán A, Hack MJP & Moin P 2018. Modeling boundary-layer transition in direct and large-eddy simulations using parabolized stability equations. Phys. Rev. Fluids 3, 023901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozano-Durán A & Jiménez J 2014a. Effect of the computational domain on direct simulations of turbulent channels up to Reτ = 4200. Phys. Fluids 26 (1), 011702. [Google Scholar]
- Lozano-Durán A & Jiménez J 2014b. Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471. [Google Scholar]
- Luchini P 2017. Universality of the turbulent velocity profile. Phys. Rev. Lett 118, 224501. [DOI] [PubMed] [Google Scholar]
- Lund TS 2003. The use of explicit filters in large eddy simulation. Comput. Math. Appl 46 (4), 603–616. [Google Scholar]
- Lund TS & Kaltenbach HJ 1995. Experiments with explicit filtering for les using a finite-difference method CTR Annu. Res. Briefs, pp. 91–105. Center for Turbulence Research. [Google Scholar]
- Lund TS, Wu X & Squires KD 1998. Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys 140 (2), 233–258. [Google Scholar]
- Marsden AL, Vasilyev OV & Moin P 2002. Construction of commutative filters for LES on unstructured meshes. J. Comput. Phys 175 (2), 584–603. [Google Scholar]
- Millikan CM 1938. A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mathematics, Harvard and MIT. [Google Scholar]
- Mizuno Y & Jiménez J 2013. Wall turbulence without walls. J. Fluid Mech. 723, 429–455. [Google Scholar]
- Moin P, Shih TH, Driver D & Mansour NN 1990. Direct numerical simulation of a three dimensional turbulent boundary layer. Phys. Fluids A 2 (10), 1846–1853. [Google Scholar]
- Nikitin N 2007. Spatial periodicity of spatially evolving turbulent flow caused by inflow boundary condition. Phys. Fluids 19 (9), 091703. [Google Scholar]
- Orlandi P 2000. Fluid Flow Phenomena: A Numerical Toolkit. Fluid Flow Phenomena: A Numerical Toolkit 1. Springer. [Google Scholar]
- Österlund JM 1999. Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, Mekanik. [Google Scholar]
- Park GI & Moin P 2014. An improved dynamic non-equilibrium wall-model for large eddy simulation. Phys. Fluids 26 (1), 015108. [Google Scholar]
- Pauley LL, Moin P & Reynolds WC 1990. The structure of two-dimensional separation. J. Fluid Mech. 220, 397–411. [Google Scholar]
- Piomelli U & Balaras E 2002. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374. [Google Scholar]
- Piomelli U, Ferziger J, Moin P & Kim J 1989. New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids A 1 (6), 1061–1068. [Google Scholar]
- Prandtl L 1925. Bericht über Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech 5, 136–139. [Google Scholar]
- Rozema W, Bae HJ, Moin P & Verstappen R 2015. Minimum-dissipation models for large-eddy simulation. Phys. Fluids 27 (8), 085107. [Google Scholar]
- Schlatter P & Örlü R 2010. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126. [Google Scholar]
- Schumann U 1975. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys 18, 376–404. [Google Scholar]
- Sillero JA, Jiménez J & Moser RD 2013. One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to δ+≈ 2000. Phys. Fluids 25 (10), 105102. [Google Scholar]
- Silvis MH, Trias FX, Abkar M, Bae HJ, Lozano-Durán A & VERSTAPPEN R 2016. Exploring nonlinear subgrid-scale models and new characteristic length scales for large-eddy simulation CTR Annu. Res. Briefs, pp. 265–274. Center for Turbulence Research. [Google Scholar]
- Simens MP, Jiménez J, Hoyas S & Mizuno Y 2009. A high-resolution code for turbulent boundary layers. J. Comput. Phys 228 (11), 4218–4231. [Google Scholar]
- Simpson RL, Moffat RJ & Kays WM 1969. The turbulent boundary layer on a porous plate: experimental skin friction with variable injection and suction. Intl J.Heat Mass Transfer 12 (7), 771–789. [Google Scholar]
- Smagorinsky J 1963. General circulation experiments with the primitive equations. Mon. Weath. Rev 91 (3), 99–164. [Google Scholar]
- Spalart PR 2009. Detached-eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202. [Google Scholar]
- Spalart PR, Jou WH, Strelets M & Allmaras SR 1997. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. Adv. DNS/LES 1, 4–8. [Google Scholar]
- Stokes GG 1901. Mathematical and Physical Papers. Cambridge University Press. [Google Scholar]
- Townsend AA 1980. The Structure of Turbulent Shear Flow. Cambridge University Press. [Google Scholar]
- Wang M & Moin P 2002. Dynamic wall modeling for large-eddy simulation of complex turbulent flows. Phys. Fluids 14 (7), 2043–2051. [Google Scholar]
- White FM & Corfield I 2006. Viscous Fluid Flow, vol. 3 McGraw-Hill. [Google Scholar]
- Wray AA 1990. Minimal-storage time advancement schemes for spectral methods Tech. Rep NASA Ames Research Center. [Google Scholar]
- Yamamoto Y & Tsuji Y 2018. Numerical evidence of logarithmic regions in channel flow at Reτ = 8000. Phys. Rev. Fluids 3, 012602. [Google Scholar]
- Yang XIA, Park GI & Moin P 2017. Log-layer mismatch and modeling of the fluctuating wall stress in wall-modeled large-eddy simulations. Phys. Rev. Fluids 2, 104601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang XIA, Sadique J, Mittal R & Meneveau C 2015. Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 27 (2), 025112. [Google Scholar]
- Yoshioka S & Alfredsson PH 2006. Control of Turbulent Boundary Layers by Uniform Wall Suction and Blowing. pp. 437–442. Springer. [Google Scholar]