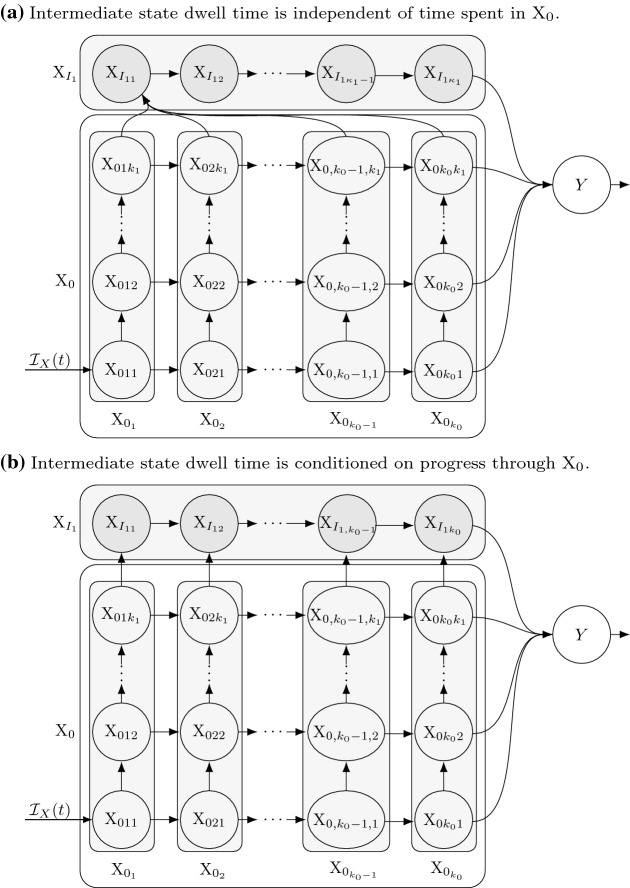
Fig. 8.

When modeling sub-state transitions, e.g., from a base state X${}_0$ to intermediate state X${}_{I_1}$ (state X$=$X${}_0\cup$X${}_{I_1}$), the intermediate sub-state dwell-time can be (a) independent of time already spent in X${}_0$ (Sect. 3.6.1, Theorem 8), or (b) conditioned on that time so that the dwell time in state X is unaffected by the sub-state transition (Sect. 3.6.2, Theorem 9). In both cases, the dwell time distribution for X${}_0$ is the minimum of independent Erlang distributions, and sub-states within X${}_0$ are as discussed in Sect. 3.5.4. Panel (a): The dwell time in X${}_{I_1}$ is Erlang(${\varrho }_1,{\kappa }_1$) and independent of time spent in X${}_0$. Thus, the sub-state transition alters the overall dwell time in state X. For the more general case, see Sect. 3.6.1 and Theorem 8. Panel (b): The overall X dwell time distribution $T_0\sim$Erlang($r_0,k_0$) is preserved by conditioning the dwell time in the intermediate state on the prior progress through sub-states of X${}_0$, as detailed in Sect. 3.6.2. Compare the transitions from X${}_0$ to X${}_{I_1}$ in these two cases, and recall Fig. 6 and the weak memoryless property of Poisson process first event times from Sect. 3.1.2