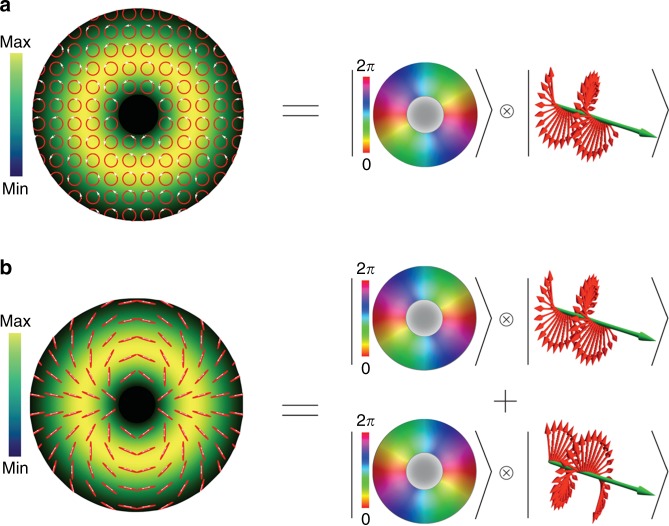
Fig. 4. Formation of vector beam with space-polarization nonseparability.
a Circularly polarized OV with an azimuthally varying phase distribution. Such a state is considered separable, as it can be represented as the product of a spatially varying vortex phase and a polarization state vector. b Spider-like vector vortex represented as the superposition of the state of a with another state with the opposite phase variation and the opposite circular polarization. From ref. 71. Reprinted with permission from AAAS