Fig. 1. Schematic of the broadband achromatic integral imaging principle and the dispersion properties of a dispersive geometrical lens, a dispersive metalens and an achromatic metalens.

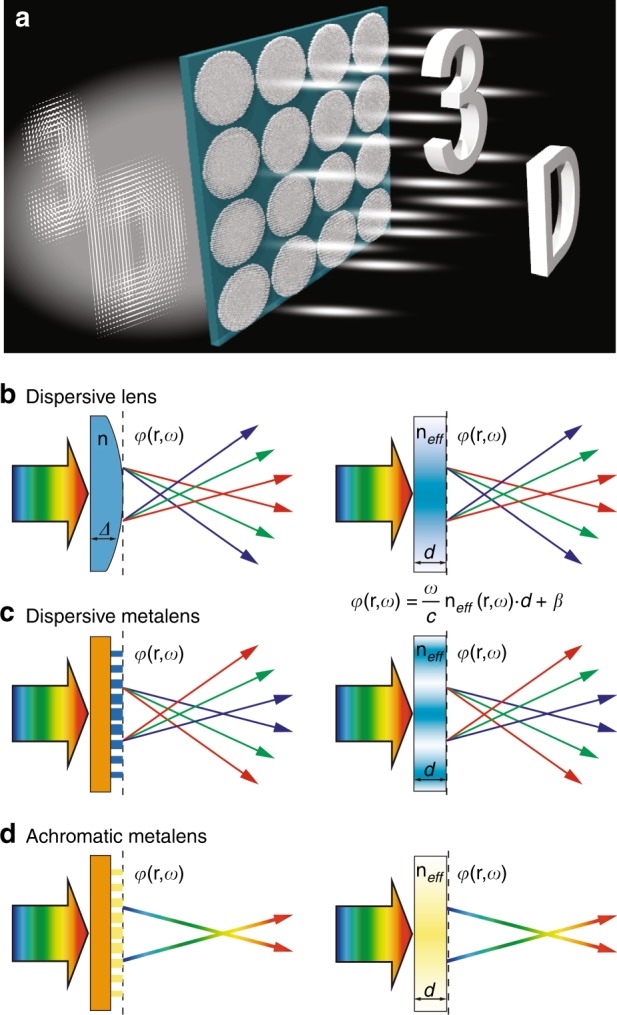
a Schematic of the broadband achromatic metalens array showing the principle of white-light achromatic integral imaging. b Dispersive geometrical lens (left) with normal dispersion in which red light is focused at longer distances than blue light. Its effective slab (right) is shown with an effective refractive index distribution n_eff(r, ω) and a given thickness d. The relationship between the exit phase φ(r, ω) and n_eff(r, ω) is φ = ω/c·n_eff·d + β, where c is the velocity of light and β is a constant. c Dispersive metalens (left) and its effective slab (right), which has a longer focal length for blue light than for red light due to the abnormal dispersion. d Broadband achromatic metalens (left) and its effective slab (right). Using the effective refractive index method, the n_eff(r, ω) distribution can be deduced by using the known φ(r, ω) of a broadband achromatic metalens