Integrative analysis of genetical genomics data incorporating network structures

Abstract

In a living organism, tens of thousands of genes are expressed and interact with each other to achieve necessary cellular functions. Gene regulatory networks contain information on regulatory mechanisms and the functions of gene expressions. Thus, incorporating network structures, discerned either through biological experiments or statistical estimations, could potentially increase the selection and estimation accuracy of genes associated with a phenotype of interest. Here, we considered a gene selection problem using gene expression data and the graphical structures found in gene networks. Because gene expression measurements are intermediate phenotypes between a trait and its associated genes, we adopted an instrumental variable regression approach. We treated genetic variants as instrumental variables to address the endogeneity issue. We proposed a two-step estimation procedure. In the first step, we applied the LASSO algorithm to estimate the effects of genetic variants on gene expression measurements. In the second step, the projected expression measurements obtained from the first step were treated as input variables. A graph-constrained regularization method was adopted to improve the efficiency of gene selection and estimation. We theoretically showed the selection consistency of the estimation method and derived the L_∞ bound of the estimates. Simulation and real data analyses were conducted to demonstrate the effectiveness of our method and to compare it with its counterparts.

1 |. INTRODUCTION

The last few decades have witnessed a rapid growth of biotechnology, which generates enormous amounts of genetic and genomics data aimed at improving our knowledge of complex traits. In quantitative trait loci (QTL) mapping studies, genotypic and phenotypic data are combined to infer the genetic architecture of a complex trait (Lander and Botstein, 1989). In expression QTL (eQTL) mapping studies, gene expression measurements and genotypes are combined, with gene expression measurements treated as quantitative traits, to understand the genetic basis of gene expression (Jansen and Nap, 2001). By unifying the two frameworks, integrative genetical genomics analysis combines phenotype, genotype, and gene expression data to obtain novel knowledge regarding the genetic basis of gene expression measurements and to provide novel insights into gene functions (Schadt et al., 2005). In addition, it is a powerful tool to dissect different gene actions such as causal, independent, and reactive gene action modes (Schadt et al. 2005). Recent developments in Gaussian graphical models (GGM) have further facilitated the discovery of gene regulatory networks using gene expression data (Meinsharsen and Bühlmann, 2006; Friedman et al., 2008). Built upon the GGM framework, covariate-adjusted GGM have been developed to combine genotypes and gene expression measurements to improve gene network inferences (Yin and Li, 2011; 2013; Cai et al., 2013). Recently, integrative modeling and testing methods combining phenotypes, genotypes, and gene expression measurements were proposed to improve the power of statistical testing (eg, Huang et al., 2014; Zhao et al., 2014). As more genomic data become available, integrative analyses of multisource genomic data could provide more comprehensive pictures of biological systems, offering opportunities for personalized medications and treatments.

Regression models have been the standard means to model the relationships between phenotypes and gene expression measurements. Because of the high costs of obtaining expression data from large numbers of samples, the sample size is typically smaller than the number of gene expression measurements. To address this issue, various regularization methods have been developed to achieve variable selection and estimation. From the biological perspective, the phenotypic response of interest and gene expression measurements are often influenced by common external confounders. These confounders are usually unobservable and cannot be explicitly modeled. Hence, their effects on the responses are usually placed in the error term. As such, the exogeneity condition in which the predictors and the error are uncorrelated, is violated when building a regression model. Consequently, the estimators obtained by the ordinary least squares method are not consistent. To overcome the endogeneity issue (ie, the predictors and errors are correlated) in a high-dimensional regression, Lin et al. (2015) developed a penalized instrumental variable (IV) regression model. Genetic variants are used as IVs because they are independent of external confounders, and they affect the phenotypic traits through gene expression measurements. The difficulties associated with the high dimensionality of genotypes and gene expression measurements are handled by regularization methods, such as the LASSO-type regressions.

Using genetic variants as IVs for causal inference, termed Mendelian randomization, has been extensively studied in the literature; see Lawlor et al. (2008) for a review. IV regression has been a popular tool in econometric studies. The classical two-stage least squares estimation method works only for low-dimensional instruments, in the sense of consistency (Chao and Swanson, 2005). Recent advancements in high-dimensional penalized regression open a door for high-dimensional IV regression in which the number of instruments can be larger than the sample size while assuming sparsity in the regression coefficients, to name a few, such as the penalized generalized method of moments (Caner, 2009; Fan and Liao, 2014) and the Dantzig selector-type penalized regression (Gautier and Tsybakov, 2011), as well as the recent method proposed by Lin et al. (2015) dealing with high dimensionality for both covariates and instruments simultaneously.

In fact, the model by Lin et al. (2015) assumes a causal model as proposed by Schadt et al. (2005). By projecting gene expression measurements into the genetic space, the projected expressions carry the effects of relevant genetic variants. Thus, the selected genes have meaningful biological interpretations compared with those selected without the projection. However, genes tend to function in complicated networks to accomplish their joint tasks (Davidson and Levin, 2005). Thus, gene expression measurements belonging to the same network (eg, a pathway) tend to be correlated. When gene expression measurements are considered in a regression model, such correlation information should be used when selecting important genes. Although the problem of variable selection in a high-dimensional regression setup has been intensively studied, many methods fail for correlated variables. Several methods have been developed to solve LASSO’s problem of tending to select only one variable from a group of highly correlated ones. Zou and Hastie (2005) proposed the elastic net method to achieve a grouping effect, which states “the coefficients of a group of highly correlated variables tend to be equal (up to a change of sign if negatively correlated).” According to Lemma 2 and Theorem 2 in their paper, if a strictly convex penalty is applied, then the higher the correlation of two variables, the smaller the upper bound of the distance of the estimated coefficients of the two variables. If the correlation is almost zero, then the two estimated coefficients are almost the same (except a minus sign if negatively correlated).

Li and Li (2008) later proposed a network-constrained method that takes advantage of the correlation information, namely network information, when performing variable selection. They introduced a Laplacian matrix and L₂ penalty to address issues introduced by correlations among variables. They applied L₂ norm to the pairwise differences of the coefficients of the correlated variables to achieve a grouping effect, and obtained theoretical results similar to those of Zou and Hastie (2005). Simulation results showed that their method works better than elastic net in cases where prior knowledge on graphical structures is available. Li and Li (2010) proposed a modified penalty function that takes into account the sign differences to encourage the absolute values of the coefficients of the connected variables to shrink toward the same value. Huang et al. (2011) proposed a sparse Laplacian shrinkage method and proved its oracle property.

Motivated by Li and Li (2008), in this paper we propose a two-step procedure to achieve variable selection and estimation under an IV regression framework by incorporating gene regulatory network structures. By adopting graphical structures as prior knowledge, we aim to address the problem of high correlations between genes in a pathway to achieve better variable selection and estimation results. Our proposed method involves a multivariate multiresponse linear model to project gene expression measurements into the genetic space. Under the assumption that each gene is only controlled by a few genetic variants, we apply the LASSO algorithm to estimate the coefficient matrix. Since genetic variables are independent of the error terms, the projected expression values are not correlated with the error terms. The projected values are then used in the second-stage estimation in which gene network structures are incorporated. We propose a graph-constrained regularization method to achieve variable selection and estimation. Assuming that certain graphical structures on gene expression measurements can be obtained either by biological experiments or by statistical estimation, two penalties (LASSO and graph-constrained penalties) are applied. The graph-constrained penalty is used to encourage the shrinking coefficients of a pair of connected variables in a network toward the same value, thus achieving a grouping effect. We theoretically evaluate the selection consistency, assuming the “graphical irrepresentable condition” and establish the upper bound of the estimates. Extensive simulation studies are conducted to evaluate the selection performance under different conditions. The utility of the method is further demonstrated by a case study.

This paper is organized as follows. In Section 1, we introduce the IV model and the two-step estimation method. Theoretical results are presented in Section 2. Simulations and real data analyses are given in Section 3 and 4, respectively, followed by a discussion in Section 5. All of the technical proofs, additional simulations and real data analyses are provided in three Supporting Information files.

2 |. STATISTICAL METHODS AND ESTIMATION

2.1 |. Motivation and the model

Let Y= (Y₁,…,Yn)^T,X = (X₁,…,X_n)^T, and G=(G₁,…,G_n)^T denote n independent and identically distributed phenotypes, gene expression measurements, and genotypes, respectively, where Y_i is a scalar, X_i = (X_i1,…, X_ip)^T is a p-dimensional vector of gene expression measurements, and Gi = (G_i1,…,G_iq)^T is a q-dimensional vector of genetic variants. In this work, we assume that both p and q could be large, and we are interested in selecting important genes (X) that could explain the variation in Y. Thus, a natural model is the following linear model:

$$\mathit{Y}=\mathit{X}\beta +\eta ,$$ (1)

where β = (β₁,…,β_p)^T is a coefficient vector and η = (η₁,…,η_n)^T is an error vector with η_i ~ N (0, σ₂₂).

Model (1) is a valid model only when X and η are independent, as defined by classical linear model theory. In practice, there are often unobservable external confounders that can affect both Y and X simultaneously. For example, living conditions or diet can affect both gene expression measurements and phenotypic traits, and their effects are typically difficult to quantify. Such unobservable factors are termed as latent variables (denoted by E). Because E are typically unobservable in practice, their effects are rendered into the error term in model (1). As such, the least squares estimates of β will not be consistent. To illustrate the concept, let us consider a simple regression model Y = βX + η(X) assuming that E affects both Y and X. Because the error term η depends on X, Dy/dX = β + dη(X)/dX, which indicates that using the ordinary least squares regression will not give consistent estimates for β unless d η(X)/ dX = 0, that is, η(X) is independent of X.

To obtain consistent estimators for β Wright (1928) introduced the IV model. As argued in Lin et al. (2015), the genetic variableG is a natural choice for the IV, because it affects Y only through X (by the central dogma) and is independent of E (by the nature of meiosis). To address the endogeneity issue and achieve selection consistency for β, Lin et al. (2015) introduced a high-dimensional IV regression model. In addition to model (1), the following second-stage model is assumed:

$$X=G\mathbf{\Gamma }+ϵ,$$ (2)

where Γ = (Γ₁,…,Γ_p) is a q × p coefficient matrix, and ϵ = (ϵ₁,…,ϵ_n)^T is an error matrix such that${\left({\in }_i^T,{\eta }_i\right)}^T$ are i.i.d. p +1 dimensional random variables following a multivariate normal distribution N(0, Σ). We write $\Sigma =\left(\begin{array}{ll}{\Sigma }_{11}\hfill & {\Sigma }_{12}\hfill \\ {\Sigma }_{21}\hfill & {\sigma }_{22}\hfill \end{array}\right)$, where Σ₁₁ represents the covarince matrix of ϵ_i,and ${\Sigma }_{12}={\Sigma }_{21}^T$ represents the covariance between ϵ_i and ηi

Assuming that G affects Y only through X (the causal model defined in Schadt et al., 2005) and that E affects both X and Y, the relationship among genotype, gene expression, and phenotype, as described in Equations (1) and (2) is presented in Figure 1. Lin et al. (2015) proposed a penalized IV regression variable selection framework to achieve selection consistency for β.

FIGURE 1.

Illustration of the instrumental variable regression model in genetical genomics analysis

Because genes function in networks to accomplish joint tasks, thus, ignoring the correlated gene network structures could lead to inconsistent selection results and the potential to miss important genes. To improve the selection performance and take advantage of the correlation among predictors to obtain better estimators, we propose a network-constrained regularization method under the high-dimensional IV regression framework.

2.2 |. Estimation of genetic effects

Under the assumption that only a few genetic variants influence gene expression measurements, the coefficient matrix Γ is assumed to be sparse. Under model (2), we apply the LASSO algorithm for each gene expression to estimate the genetic effects. The estimation issue can be formulated as the following p optimization problem:

$${\widehat{\Gamma }}_j=\underset{{\Gamma }_j}{\text{arg min}}\left[\frac{1}{2n}{\left(X^j-\mathit{G}{\Gamma }_j\right)}^T\left(X^j-\mathit{G}{\Gamma }_j\right)+{\lambda }_j\Vert {\Gamma }_j{\Vert }_1\right],$$ (3)

where λ_j, j = 1,…,p are tuning parameters,∥·∥₁ refers to the L₁,…, norm, and X^j = (X_1j,…, X_nj)^T, j =1,…,p. The estimate of Γ is denoted as $\widehat{\mathbf{\Gamma }}=\left({\widehat{\Gamma }}_1,\dots ,{\widehat{\Gamma }}_p\right)$. Similar to Friedman et al. (2007) and Friedman et al. (2010), we applied cross-validation to select λ_j, j = 1,…,p, using the default method in the R package glmnet.

2.3 |. Network-constrained regularization

Once we obtain an estimate of the coefficient matrix Γ, we determine the fitted values of X using $\widehat{X}=G\widehat{\Gamma }$, which can also be viewed as the projected values of X in the Gr space. We then substituted in the $\widehat{X}$ second X step to select important X variables that carry the effects of G on the response Y.

To adjust for the effects of correlations among gene expression measurements in a network on gene selection, we consider the following optimization problem under a network-constrained penalized regression framework (Li and Li, 2008):

$$\widehat{\mathit{\beta }}=\underset{\beta }{\text{arg min}}\left\{\frac{1}{2n}\sum _{i=1}^n{\left(Y_i-\sum _{j=1}^p{\widehat{X}}_{ij}{\beta }_j\right)}^2+p_{\lambda ,\alpha }(\beta )\right\},$$ (4)

$$p_{\lambda ,\alpha }(\beta )=\lambda \left[\alpha \sum _{j=1}^p\left|{\beta }_j\right|+\frac{1-\alpha }{2}\sum _{k~t}\left|r_{kt}\right|{\left({\beta }_k-s_{kt}{\beta }_t\right)}^2\right],$$ (5)

where r_kt represents the weight of the correlation strength between two variables, s_kt = sign(r_kt),λ>0 and α ∈ [0, 1] are tuning parameters, and k~t indicates that the rth and tth nodes are correlated, that is, r_kt ≠0.function in Equation (5) includes two penalties that are used to select variables and to handle the problems of correlations, while encouraging the coefficients of two correlated variables to shrink to the same value, achieving grouping effect.

We apply the coordinate descent algorithm to solve the optimization problem. We first center the response variable Y and standardize ${\widehat{X}}_j,j=1,\dots ,p$. Taking the first derivative with respect to β_h, h ∈ {1,…,p}:

$$\frac{\partial }{\partial {\beta }_h}\left\{\frac{1}{2n}\sum _{i=1}^n{\left(Y_i-\sum _{j=1}^p{\widehat{X}}_{ij}{\beta }_j\right)}^2+p_{\lambda ,\alpha }(\mathit{\beta })\right\}=-\frac{1}{n}\sum _{i=1}^n\left(Y_i-\sum _{j\ne h}{\widehat{X}}_{ij}{\beta }_j\right)-\lambda (1-\alpha )\sum _{h\sim j}{r}_{hj}{\beta }_j+\left(1+\lambda (1-\alpha )\sum _{h\sim j}\left|r_{hj}\right|\right){\beta }_h+\lambda \alpha \frac{{\beta }_h}{\left|{\beta }_h\right|}.$$

Setting

$$\frac{\partial }{\partial {\beta }_h}\left\{\frac{1}{2n}{\sum _{i=1}^n\left(Y_i-\sum _{j=1}^p{\widehat{X}}_{ij}{\beta }_j\right)}^2+P_{\lambda ,\alpha }\left(\beta \right)\right\}=0,$$

we obtain the solution as

$$S((1/n){\sum }_{i=1}^n\left(Y_i-{\sum }_{j\ne h}{\widehat{X}}_{ij}{\beta }_j\right){\widehat{\beta }}_h=\frac{+\lambda (1-\alpha ){\sum }_{h\sim j}{r}_{hj}{\beta }_j,\lambda \alpha )}{1+\lambda (1-\alpha ){\sum }_{h\sim j}\left|r_{hj}\right|}.$$ (6)

Similar to Friedman et al. (2007) and Friedman et al. (2010), we set ${\lambda }_{\text{max}}={\text{max}}_j\left|\langle {\widehat{X}}_j,Y\rangle \right|/n\alpha$ and λ_min = θλ_max, where θ = 0.001, and construct a sequence of K values of λ, decreasing from λ_max to λ_min on the log scale, to run a grid search to find the optimal λ. We use cross-validation to choose the tuning parameters λ and α.

Based on the theorem in the next section, we can calculate the maximum λ such that all the β coefficients are shrunk to zeros. This provides an upper bound of the search space for the tuning parameter and reduces the search space of λ In practice, we choose λ by cross-validation (CV) or Bayesian information criterion (BIC) method for preset values of λ. Since the λ goes to 0, we can set λ denser for smaller values than large ones, for example using the log-space function in R. As we adopted the coordinate decent (CD) algorithm, we can calculate the solution path from large to small λ’s. The CD algorithm warms up for the first several λ’s which can speed up the calculation.

2.4 |. Theoretical results

The selection consistency for the on-step network-constrained penalization method has been studied (Li and Li, 2008; 2010). However, the consistency property for the proposed two-stage estimation has not been established. In fact, given the estimation error from the first step, the establishment of selection consistency is not trivial. Here, we present the theoretical results on the variable selection and estimation for the proposed high-dimensional IV regression model. We adopt the notations used in Lin et al. (2015). For a matrix $A,\Vert A{\Vert }_1={\text{max}}_j{\sum }_t\left|a_{ij}\right|$ and $\Vert A{\Vert }_{\infty }={\text{max}}_t{\sum }_j\left|a_{ij}\right|$ For a vector α, a matrix A, and index sets I and J, α_I and A_IJ denote the subvector and the submatrix. J^c denotes the complement of J and |J| denotes the number of elements in J. We define the restricted eigenvalue for the matrix A_n×m and 1≤s≤m by

$$\kappa (\mathit{A},s)=\underset{\left|J\right|\le s}{\text{min}}\underset{\underset{{\Vert {\delta }_{J}C\Vert }_1\le 3{\Vert {\delta }_J\Vert }_1}{\delta \ne 0}}{\text{min}}\left\{\Vert \mathit{A}\delta {\Vert }_2/\left(\sqrt{n}{\Vert {\delta }_J\Vert }_2\right)\right\}.$$

Let $r={\text{max}}_{1\le j\le p}\left|supp\left({\Gamma }_j\right)\right|$ ,s=supp(β), s = |S| and ${\sigma }_{\text{max}}={\text{max}}_{1\le j\le p}{\sigma }_j$ ,where supp(.) is the supportive set. We assume $\Vert \mathbf{\Gamma }{\Vert }_1\le M_1$ and $\Vert \beta {\Vert }_1\le M_2$ for some positive constants M₁ and M₂ We write the penalty function in (5) as $p_{\lambda ,\alpha }(\beta )=\lambda \left[\alpha \sum _{j=1}^p\left|{\beta }_j\right|+(1-\alpha ){\beta }^T\mathit{L}\beta /2\right]$, where

$$={\mu }_1{\sum }_{j=1}^p\left|{\beta }_j\right|+{\mu }_2{\beta }^T\mathit{L}\beta$$

μ₁ = λα and μ₂ = λ (1 − α)/2. L represents a nonnegative definite matrix equipped with the graphical information. We assume ||Lβ||_∞ <C_L, for some constant C_L and define $C={(G\Gamma )}^{T}G\Gamma /n$, $\varphi ={\Vert {\left(C_{SS}+2{\mu }_2{L}_{SS}\right)}^{-1}\Vert }_{\infty }$ and $b_0={\text{min}}_{J\in S}\left|{\beta }_j\right|$. To control the estimation errors in the first and second steps, the following conditions are imposed:

• (C1) $\kappa (G,r)\ge \kappa \text{ for some }\kappa >0.$

• (C2) $\Vert \left(C_{S^{c}S}+2{\mu }_2{L}_{S^{c}S}\right){\left(C_{SS}+2{\mu }_2{L}_{SS}\right)}^{-1}{\Vert }_{\infty }<1-\alpha ,\text{ where }\alpha \text{ is a constant and }0<\alpha <1.$

Remark 1. We allow p,q,r,s, and κ to depend on the sample size n. Part of our derivation is based on the theorem of the estimation and prediction loss of $\widehat{\Gamma }$ established in Lin et al. (2015). To obtain the selection consistency and the L_∞ bound, we impose an assumption on GΓ which is similar to the irrepresentable condition in Zhao and Yu (2006).

Remark 2. (C1) is used to ensure that we can obtain a good estimate at the first stage. (C2) requires that the predictors correlated with the response and those that do not relate to the response are not highly correlated. This is the graphical irrepresentable condition for group lasso. Like the argument in Zhao and Yu (2006), (C2) requires the “regression coefficients” of the irrelevant covariates on the relevant covariates be less than 1. In Lemma 1 of the Supporting Information File, we prove that condition (C2) holds for the sample covariance matrix of $\widehat{X}$ with a smaller α. Using these, we establish the following theorem on the selection consistency of $\widehat{\beta }$

Theorem 1. If the regularization parameters in the first step are selected as ${\lambda }_j=C{\sigma }_j\times \sqrt{(\text{log }p+\text{log }q)/n}$ and satisfy $16\varphi rs{\lambda }_{\text{max}}\left(2M_1+{\lambda }_{\text{max}}\right)/{\kappa }^2\le 0.5\alpha /(4-\alpha )$ where $C>2\sqrt{2}$ and ${\lambda }_{\text{max}}={\text{max}}_{1\le j\le p}{\lambda }_j$ the regularization

parameters in the second step are selected as ${\mu }_1=C_0/\kappa \times \sqrt{r(\text{log }p+\text{log }q)/n}$ and ${\mu }_2{C}_L\le (\alpha (16-3\alpha )/4(4-\alpha )(8-3\alpha )){\mu }_1$,where $C_0=c_0{M}_1\text{max}\left({\sigma }_{p+1},M_2{\sigma }_{\text{max}}\right)$ with c₀,> 0,b₀ has a lower bound

$$b_0>\frac{2(4-\alpha )}{8-3\alpha }\varphi \left[\frac{8-\alpha }{2(4-\alpha )}{\mu }_1+2{\mu }_2{C}_L\right],$$

and further assume that (C1) and (C2) hold, then with a probability of at least1− c₁ (pq)^−c2, where c₁, c₂ > 0, $\widehat{\beta }$ obtained from (6) satisfies

$$\text{sign} (\widehat{\beta })= \text{sign} (\beta ),{\Vert {\widehat{\beta }}_S-{\beta }_S\Vert }_{\infty }\le \frac{16(4-\alpha )\varphi C_0}{{(8-3\alpha )}^2\kappa }\sqrt{\frac{r(\text{log }p+\text{log }q)}{n}}.$$

The proof of the theorem is given in the Supporting Information Appendices.

3 |. SIMULATION

We conducted extensive simulation studies to evaluate the finite sample performance of the proposed method. Here, we closely followed the simulation setup proposed in Lin et al. (2015), but imposed certain correlation structures on genes to show the impact of network structures on variable selection and estimation. We simulated a total of p variables of gene expression and considered three group structures on β with five variables in each group. Within each group, the variables are correlated. The strength of the correlation was controlled by the number of effective SNPs they had in common. Two groups of variables had nonzero coefficients and the third group had zero coefficients. The rest of the p − 15 variables had zero coefficients and had no graph structure, that is, $\beta ={\left({\beta }_1,\underset{}{\underbrace{\dots }},{\beta }_{5_5},{\beta }_6,\underset{}{\underbrace{\dots }},{\beta }_{{10}_5},0,\underset{}{\underbrace{\dots }},0_5,0,\underset{}{\underbrace{\dots }},0_{p-15}\right)}^T.$ Simulating a structured group with zero coefficients was done for comparison purposes. Two simulation scenarios were considered. In scenario 1, we set all of the nonzero coefficients to 0.5 (ie,βk = 0.5 for k = 1,…, 10), while in scenario 2,βk ~ U (0.5, 1) for k = 1,…,10. Again, the two scenarios were for the purpose to compare the robustness of the method.

For the covariance matrix $\text{cov}\left(\in ,\eta \right)=\Sigma =\left(\begin{array}{ll}{\Sigma }_{11}\hfill & {\Sigma }_{12}\hfill \\ {\Sigma }_{21}\hfill & {\sigma }_{22}\hfill \end{array}\right)$ the ith row and jth column entry in Σ₁₁ was set to be ${(0.2)}^{|i-j|}$ for i,j = 1,…,p, and σ₂₂=1. To correlate η and the 15 X variables with a graph structure, we set the 15 entries in the last columns of Σ₁₂ as 0.23 and the rest as 0. Then we simulated (ϵ, η) ~ N_p+1(0, Σ). For simplicity,G was generated by sampling from a Bernoulli distribution with success probability 0.5, even though a multinomial distribution with three genotypic categories for an additive genetic model can be assumed.

To simulate X, we generated the coefficient matrix Γ first. As mentioned earlier, the graph structure in X was controlled by the number of commonly shared G variables. The more they had in common, the stronger the correlation between them. We assumed the number of common SNPs to be 3, 4, or 5 to achieve different correlation strengths. The corresponding coefficients in Γ were set to be independent realizations from U (0.75, 1). Here each column of Γ was a coefficient vector corresponding to an expression variable. For the rest of the columns of Γ corresponding to the X variables without a structure, five nonzero entries from each column were randomly selected and their values were independently sampled from U ([−1, −0.75] ∪ [0.75, 1]). Then we generated X and Y using X = ΓG +ϵ and Y= β^TX +η.

We considered both low- and high-dimensional situations in our simulation. In the low-dimensional case, we set p = 100, q = 100 and varied n from 200 to 1400 when both p and q were fixed. In the high-dimensional case, we set p = 600, q = 600, and n = 300. We compared our method, IV regression with graph-constrained regularization (denoted as IVGC), with the method proposed by Lin et al. (2015), which was an IV regression only model (denoted as IV). The measurements we used to evaluate and compare different methods and setups were the numbers of correctly estimated nonzero coefficients (true positive), $\Vert \widehat{\beta }-\beta {\Vert }_2$ (estimation loss), $n^{-1/2}\Vert X(\widehat{\beta }-\beta ){\Vert }_2$ (model error), and Matthews correlation coefficient $(MCC=(TP\times TN-FP\times FN)/\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)})$ where TP = true positive, TN = true negative, FP = false positive, and FN = false negative. TN was defined as the number of correctly estimated zero coefficients; FP was defined as the number of incorrectly estimated nonzero coefficients; and FN was defined as the number of incorrectly estimated zero coefficients. The greater the MCC value, the better the variable selection performance. The reason that we chose model error instead of prediction error is explained in Lin et al. (2015). We used cross-validation to choose the penalty tuning parameters. For each case, we ran 200 replications, and reported the sample means and standard errors.

Table 1 shows the results for the low-dimensional situation with n = 600. As introduced in the simulation setup, the greater the number of shared SNPs (numSNP in the table), the stronger the correlation between the expression variables. IVGC had smaller estimation and model errors in the two scenarios at different β values. For TP, both IVGC and IV performed similarly when numSNP was 3 or 4 (weak correlation compared to with numSNP = 5). When numSNP increased to 5, IVGC had a higher TP rate than IV. IV implemented a LASSO penalty that only randomly picks one among the correlated variables. Introducing a graph-constrained penalty achieved the selection consistency when graphical structures are present. For MCC, IVGC and IV had quite similar performances, although IVGC had a slightly larger MCC. In general, IVGC performed better compared with IV in both variable selection and estimation.

TABLE 1.

Simulation results for p = 100, q = 100, n = 600

Method	numSNP	Estimation loss	Model error	True positive	False positive	MCC
IVGC		βk = 0.5, k = 1,…,10
	3	0.65 (0.31)	0.33 (0.12)	10 (0)	4.67 (3.72)	0.82 (0.11)
	4	0.65 (0.30)	0.35 (0.12)	9.99 (0.07)	4.05 (3.51)	0.84 (0.11)
	5	1.19 (1.22)	0.55 (0.41)	9.72 (0.96)	3.35 (3.22)	0.85 (0.11)
		βk ~ U (0.5, 1), k = 1,…,10
	3	1.24 (0.35)	0.57 (0.13)	9.99 (0.07)	4.5 (3.49)	0.83 (0.11)
	4	1.48 (0.40)	0.69 (0.15)	9.99 (0.07)	4.00 (3.70)	0.84 (0.11)
	5	1.98 (1.64)	0.90 (0.53)	9.76 (0.87)	2.96 (3.05)	0.86 (0.12)
IV		βk = 0.5, k = 1,…,10
	3	1.51 (0.4)	0.64 (0.13)	10 (0)	5.09 (3.75)	0.81 (0.11)
	4	1.86 (0.47)	0.77 (0.16)	9.96 (0.18)	4.26 (3.57)	0.83 (0.11)
	5	4.36 (0.78)	1.59 (0.29)	7.61 (1.01)	3.68 (3.29)	0.70 (0.13)
		βk ~ U (0.5, 1), k = 1,…,10
	3	1.99 (0.60)	0.85 (0.19)	9.97 (0.16)	5.30 (3.91)	0.80 (0.11)
	4	2.71 (0.71)	1.12 (0.24)	9.95 (0.23)	4.75 (3.73)	0.82 (0.11)
	5	5.89 (1.29)	2.22 (0.46)	7.99 (1.01)	2.92 (2.65)	0.75 (0.12)

Abbreviation: IV, instrumental variable; IVGC, IV regression with graph-constrained regularization.

The numbers in the parentheses are the empirical SE.

We also varied the sample size n but fixed p and q. The results are shown in Figure 2. Both methods performed better as the sample size increased. IVGC completely dominated IV in terms of estimation loss and model error. In addition, IVGC had a slightly larger MCC value compared with that of IV. Both methods performed quite similarly in terms of TP, especially when n was large. A detailed comparison can be found in Table 2, along with the standard errors given in the parentheses.

FIGURE 2.

Results for fixed p(=100) and q(=100) but varying n (200~1400). IV, instrumental variable; IVGC, IV regression with graph-constrained regularization [Color figure can be viewed at wileyonlinelibrary.com]

TABLE 2.

Simulation results for p = 100,q= 100, n = 200~1400 and numSNP = 4

n	Method	Estimation loss	Model error	True positive	MCC
200	IVGC	1.29 (0.77)	0.72 (0.28)	9.93 (0.41)	0.83 (0.11)
	IV	3.20 (0.78)	1.32 (0.27)	9.30 (0.76)	0.79 (0.12)
400	IVGC	0.86 (0.43)	0.47 (0.15)	9.98 (0.20)	0.83 (0.11)
	IV	2.34 (0.63)	0.95 (0.20)	9.77 (0.47)	0.80 (0.11)
600	IVGC	0.62 (0.34)	0.35 (0.12)	10.00 (0.00)	0.86 (0.11)
	IV	1.82 (0.49)	0.75 (0.15)	9.96 (0.20)	0.83 (0.11)
800	IVGC	0.55 (0.25)	0.29 (0.09)	10.00 (0.00)	0.83 (0.11)
	IV	1.70 (0.42)	0.68 (0.14)	9.99 (0.10)	0.82 (0.11)
1000	IVGC	0.49 (0.22)	0.26 (0.09)	10.00 (0.00)	0.83 (0.11)
	IV	1.47 (0.38)	0.60 (0.12)	10.00 (0.00)	0.80 (0.11)
1200	IVGC	0.45 (0.18)	0.24 (0.08)	10.00 (0.00)	0.85 (0.11)
	IV	1.29 (0.33)	0.53 (0.11)	10.00 (0.00)	0.83 (0.10)
1400	IVGC	0.43 (0.19)	0.23 (0.07)	10.00 (0.00)	0.83 (0.11)
	IV	1.25 (0.33)	0.50 (0.10)	10.00 (0.00)	0.83 (0.12)

Abbreviation: IV, instrumental variable; IVGC, IV regression with graph-constrained regularization.

The numbers in the parentheses are the empirical SE.

Table 3 shows the results in the high-dimensional situations. The observed patterns were similar to those found in the low-dimensional cases. In general, IVGC performed as well as, or better, than IV.

TABLE 3.

Simulation results for p = 600,q= 600, and n = 300

Method	numSNP	Estimation loss	Model error	True positive	MCC
IVGC	βk = 0.5, k = 1,…,10
	3	1.65 (1.08)	0.73 (0.27)	10.00 (0.00)	0.74 (0.14)
	4	1.68 (0.91)	0.84 (0.25)	9.98 (0.14)	0.78 (0.15)
	5	2.93 (1.76)	1.25 (0.51)	9.13 (1.38)	0.75 (0.15)
	βk ~ U(0.5, 1), k = 1,…,10
	3	2.59 (0.94)	1.22 (0.27)	9.99 (0.10)	0.74 (0.12)
	4	2.62 (1.04)	1.37 (0.36)	9.91 (0.45)	0.78 (0.13)
	5	4.36 (2.64)	1.93 (0.70)	9.15 (1.42)	0.75 (0.18)
IV	βk = 0.5, k = 1,…,10
	3	2.95 (1.21)	1.13 (0.25)	9.84 (0.39)	0.70 (0.14)
	4	3.28 (1.21)	1.31 (0.28)	9.63 (0.56)	0.73 (0.15)
	5	4.86 (1.23)	1.77 (0.35)	7.71 (1.03)	0.64 (0.15)
	βk ~ U(0.5, 1), k = 1,…,10
	3	3.86 (1.48)	1.61 (0.35)	9.90 (0.30)	0.71 (0.13)
	4	4.45 (1.10)	1.86 (0.35)	9.66 (0.59)	0.72 (0.12)
	5	6.91 (1.69)	2.64 (0.44)	7.87 (1.08)	0.65 (0.16)

Abbreviation: IV, instrumental variable; IVGC, IV regression with graph-constrained regularization.

The numbers in the parentheses are the empirical SE.

We also did additional simulations as suggested by the reviewers. Due to space limit, we rendered those additional simulations into Supporting Information File 1. Specifically, we did additional simulations to check the robustness of the method by reducing the regression effect size, compared the performance of IVGC with on-stage LASSO, and with IV by mimicking real situations, evaluated the impact of ignoring IVs and the impact on false positive control by imposing a network structure on null genes. We also simulated data assuming a high correlation (ρ= 0.8) between the X variables and checked the impact of the correlation on the second-stage estimation and selection. The results were reported in Table S6. Compared to Table 2 results (ρ= 0.2), no large difference was observed, indicating that the first-stage LASSO algorithm is generally safe to apply even though there are strong correlations among the X variables. After regressing each X variable against the G variables, the correlations among the fitted values $\widehat{X}$ are largely determined by the G variables they share in common.

4 |. REAL DATA APPLICATIONS

We applied our method to a human liver cohort data set to show the utility of the method. The data contain genotypes, gene expression measurements, and pheno types of enzyme activities and can be downloaded from the Sage Bionetworks’ synapse platform using Synapse ID syn4499. For details of the data set, please refer to Schadt et al. (2008) and Yang et al. (2010). The phenotypes are enzyme activity measurements of Cytochrome P450.

There are 170 individuals measured for 18 556 gene transcripts, 449 699 SNPs, and some covariates such as gender and age. There are a total nine enzyme activity measures and we focused on CYP2E1 in our analysis. It was the only measure to pass the Shapiro-Wilk normality test (P > 0.1) after a log-transformation. We regressed the log-transformed CYP2E1 over the covariates gender and age, and used the covariate-adjusted responses for the following analysis.

SNPs with a genotyping call rate of less than 90% or a minor allele frequency of less than 5% were removed from the data set, leaving 312 082 SNPs. Here, we focused on the KEGG pathway “Metabolism of Xenobiotics by Cytochrome P450” (hsa00980) to select important genes associated with CYP2E1 activity. There were 76 genes in this pathway (see the Supporting Information File for a full list) and 70 were mapped to our data set. We fit a linear regression model for each gene transcript to select the top 1000 SNPs according to their marginal P values. Then, we fit a multiple regression model with the 1000 SNPs and estimated their coefficients using the LASSO algorithm. The fitted values for the 70 gene transcripts were obtained and the IVGC method was applied to select important genes. We obtained the graph structure of the 70 genes in this pathway from the KEGG pathway database using the R package KEGGgraph. The weight function was set as 1 if the two genes were connected in the pathway. Otherwise, it was set as zero. When the true graph structure or the network connectivity information can be accurately inferred from the data, we can adopt the actual correlation as the weight information. However, estimating the graph structure or the network information can be less reliable due to small sample size or gene expression measurement errors. Thus, using the edge information as 1 or 0 inferred from known biological pathways can be an alternative choice. Chang et al. (2018) suggested to use 1 or 0 as the edge weight information due to the uncertainty of estimating the weight. Stability selection (Meinsharsen and Bühlmann, 2010; Shah and Samworh, 2013) was applied to obtain a stable variable selection result. Each time we randomly selected 80% of the data to run our algorithm and the selection was repeated 100 times. Then, the percentage of selection for each gene was calculated as the selection rate. The higher the selection rate, the more important the gene’s effect on CYP2E1 activity. In addition to report the result by the stability selection, we also reported the prediction accuracy of the proposed method compared with the IV, the regular one-step LASSO estimation (1LASSO) and a two-stage elastic net algorithm without incorporating the graph information (EN). We did a leave-one-out cross-validation, by using the n −1 data to train the model and then calculating the squared prediction error by ${\left(Y_{-i}-{\widehat{Y}}_{-i}\right)}^2$, where $Y_{-i}$ and ${\widehat{Y}}_{-i}$ are the original and the predicted response for the ith testing data, respectively. We repeated for all the n = 170 observations and calculated the mean-squared prediction error (MSPE) by MSPE =∑ⁿ_i=1(Y_−i −Ŷ_−i)2/n. The MSPE for IVGC, IV,EN, and 1LASSO were 0.4909, 0.4974, 0.5212, and 0.5015, respectively, indicating good prediction accuracy of the method incorporating the network information, although the difference is not very large.

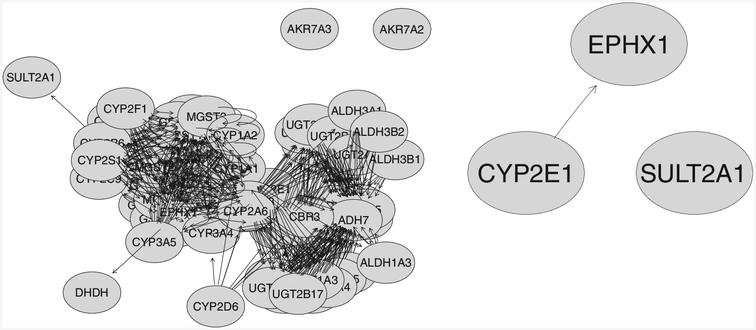
Table 4 shows the top three genes selected using the IVGC, IV, and EN methods with a selection threshold π_thr = 0.6, a suggested lower bound in the stability selection paper by Meinsharsen and Bühlmann (2010). The three methods select the three genes with quite similar selection rate. Among the listed genes, gene CYP2E1 was selected in 100% of the runs using the IVGC method compared with 99% for the IV and EN method. We expected that the gene would be selected every time because the response was a measure of the gene’s activity. The high selection rate indicated the robustness of our method when network information was incorporated. The three selected genes are functionally related to xenobiotic and human liver function. The CYP2E1 gene encodes an enzyme involved in the metabolism of drugs, hormones, and xenobiotic toxins (Wang et al., 2009). The EPHX1 (microsomal epoxide hydrolase) gene is a bifunctional protein showing in two distinct topologic orientations. The type 1 form plays a central role in hepatic metabolism of xenobiotics (Peng et al., 2015). The SULT2A1 gene encodes dehydroepiandrosterone sulfotransferase, which catalyzes the 3ʹ-phosphoadenosine 5ʹ-phosphosulfate-dependent sulfation of a large variety of steroids in human liver and adrenal tissue and is responsible for sulfation of bile acids in human liver (Comer et al., 1993). However, further biological validation is needed to discern the real relationships of these genes with the enzyme’s activity. A complete list of the genes in the pathway is given in Supporting Information 1. Figure 3 shows the full KEGG connectivity information of the 70 genes in this pathway and the extracted connectivity information for the top three genes shown in Table 4. The selected SNPs (eQTL) associated with each one of the three genes can be found in Table S0 in Supporting Information File 1, along with their chromosome location, genomic position, dbSNP_rsID, and gene symbol. We did not observe strong cis-acting effect.

TABLE 4.

List of the top genes with a stability selection rate >60% by using any one of the three methods (IVGC, IV and EN) for pathway hsa00980

Gene symbol	IVGC	IV	EN
CYP2E1	1.00	0.99	0.99
EPHX1	0.99	0.98	0.99
SULT2A1	0.89	0.84	0.92

Abbreviation: IV, instrumental variable; IVGC, IV regression with graph constrained regularization.

FIGURE 3.

The network structure of the 70 genes (left figure) and the top three selected genes listed in Table 4 (right figure) from KEGG “Metabolism of Xenobiotics by Cytochrome P450” pathway, extracted using the R package KEGGgraph

We also picked another pathway in the KEGG database, the “Drug metabolism-cytochrome P450” pathway (hsa00982). This pathway contains a total of 72 genes (see https://www.genome.jp/dbget-bin/www_bget?hsa00982 for a full list of the genes). Sixty-six genes were found in this dataset. We applied the proposed IVGC method and the IV and EN methods without network penalty. Table 5 shows the stability selection results. We listed the top 12 genes with a selection rate> 0.6 by using any one of the methods. Again, IVGC has the highest select rate for gene CYP2E1.

TABLE 5.

List of the top genes with a stability selection rate >60% by using any one of the three methods (IVGC, IV and EN) for pathway hsa00982

Gene symbol	IVGC	IV	EN
CYP2E1	1	0.98	0.99
AOX1	0.96	0.88	0.94
CYP2D6	0.89	0.48	0.7
UGT1A1	0.89	0.46	0.65
UGT1A9	0.86	0.33	0.48
MAOB	0.83	0.3	0.55
CYP3A4	0.79	0.06	0.14
CYP2C19	0.75	0.16	0.38
GSTO2	0.71	0.28	0.47
GSTM3	0.7	0.22	0.48
UGT1A5	0.67	0.01	0.17
FMO2	0.66	0.17	0.41

Abbreviation: IV, instrumental variable; IVGC, IV regression with graph-constrained regularization.

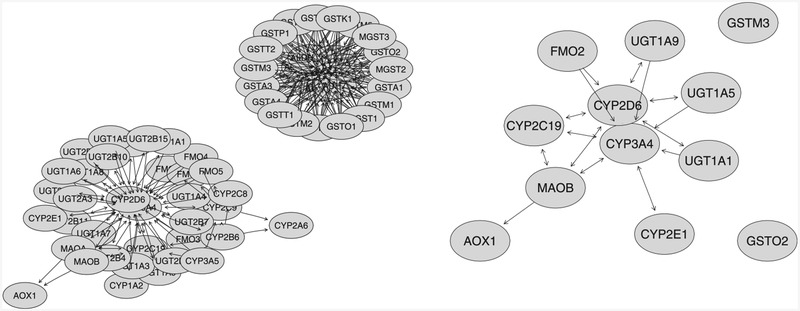
Overall, IVGC has higher selection rate than IV and EN without considering the graph information. The network plot of the 66 genes as well as the top 12 genes is shown in Figure 4 using the R package KEGGgraph. From the right figure in Figure 4, genes CYP2D6 and CYP3A4 show relatively more connections than any other genes. By incorporating the graph information, the proposed two-stage IVGC method can robustly select these genes with high stability selection rates, while IV or EN did not. Similar pattern was observed for gene UGT1A5. This again demonstrates the advantage of incorporating the graph information in gene selection. Noted that the network structure for this pathway is very different from the “Metabolism of Xenobiotics by Cytochrome P450” pathway (hsa00980) analyzed before. All the top genes have been shown to have predominant expressions in adult human liver. The leave-one-out cross-validation prediction errors are 0.5057, 0.5089, and 0.5110 corresponding to IVGC, IV, and EN, respectively. IVGC has the smallest prediction error among the three. The SNPs (eQTL) of each gene listed in Table 5 were reported in Supporting Information File 3. Again, we did not observe strong cis-acting eQTL. It is interesting to note that three genes located on chromosome 2, namely, UGT1A1, UGT1A5, and UGT1A19, share a large number of eQTL.

FIGURE 4.

The network structure of the 66 genes (left figure) and the top 12 selected genes listed in Table 5 (right figure) from KEGG “Drug metabolism-cytochrome P450” pathway, extracted using the R package KEGGgraph

We also analyzed additional 65 pathways randomly picked from different categories in the KEGG pathway database following the same procedure described in the paper. Due to space limit, we rendered the results to Supporting Information File 2. Among the 65 pathways analyzed, four pathways have zero genes passed the 0.6 selection rate threshold, implying a less important role of these pathways on CYP2E1 activity. Among the rest 61 pathways, IVGC has smaller prediction errors than IV and EN in 26 pathways. In many cases, the prediction errors of the three methods are quite similar. The results indicate that IVGC may not always perform the best in terms of prediction error. It also depends on the underlying pathway connectivity structure and the nature of the gene functional mechanism in a relationship to the activity of CYP2E1 enzyme. In most cases, when gene connectivity is relatively sparse, the gene stability selection rates of IVGC and IV are quite close. When gene connectivity is relatively dense, the gene stability selection rates of IVGC and EN are quite similar. This demonstrates the relative robustness of the IVGC method.

5 |. DISCUSSION

Gene selection using computational tools is a cost and tim-efficient way to identify important genes for further biological validation. Thus, developing robust selection methods has been a central task to achieve this goal. Lin et al. (2015) proposed an IV regression framework to address the endogeneity issue in genetical genomic data analyses. Because genes function in networks to achieve their joint tasks, we have proposed a graph-constrained selection and estimation method under an IV regression framework. Our model is an extension of the work by Lin et al. (2015) while incorporating prior knowledge of the graph structures of genes that belong to a network (eg, pathway). We established the selection consistency under the proposed two-step estimation procedure and showed the L_∞ bound that provides theoretical insights into the properties of our method.

Intensive simulations were conducted to evaluate the model’s performance while comparing it with the IV regression method (Lin et al., 2015). Because the authors have demonstrated the advantage of the IV regression over a naive regression without considering IVs (Lin et al., 2015), we did not include a comparison of our method with the naive method in this work. We applied our method to a human liver cohort data set to demonstrate the effectiveness of our method. The stability evaluation results indicated the robustness of our method compared with the IV method without considering the real biological regulatory relationship.

In our work, the first-stage estimation is done with the LASSO algorithm. At the second stage, a graph penalty is applied to encourage genes with edges to be selected together. Our first-stage estimation does not consider correlations among the X variables. This strategy, however, is safe to apply in general. After regressing each X variable against all G variables, the correlation between two fitted values is mainly determined by the number of G variables they share in common. That is, after projecting the X variables to the column space spanned by G variables, the correlation of the projected values is mainly determined by how many G variables they share in common. The original correlation has little impact on the correlations among the fitted values, hence on the graph penalty and the selection results. Thus, the proposed LASSO estimation at the first stage is safe to apply. As we demonstrated in our simulation studies (see Table 2 and Table S6), the correlation has little impact on the selection and estimation performance. The other option is to employ the “MRCE” method proposed by Rothman et al. (2010) in which the regression coefficients and covariance matrix can be simultaneously estimated in a sparse multivariate multiple regression setup. However, this method may have computational issues when the data dimensions (both p and q) are high.

In general, LASSO does not have the oracle property. It is possible that the estimation errors of the coefficients cannot be reduced to zero even under large samples. SCAD and MCP are natural alternatives that enjoy the oracle property (Fan and Li, 2001; Zhang, 2010). Both penalties can be applied in our procedure to replace the lasso penalty. We will consider these penalties in our future work, although substantial modifications may be needed for the proof of the selection consistency.

When applying the graph-constrained penalization method, the graphical structure needs to be available before the penalized estimation is applied. The network structure is very important to the success of the estimation procedure. One has to be careful in borrowing the network information. Chang et al. (2018) has discussed the similar issue via simulation studies. Their results show that imposing wrong network structure can increase both false positive and false negatives and lower the prediction performance. Statistically speaking, one can estimate the network information using methods such as the graphical model estimation methods in the literature. However, the accuracy of the estimated network is subject to sample size and various other issues. Thus, in practice, one should try to borrow network information from reliable resources such as using the KEGG pathway information, unless one can get a quite robust estimation in network structures with large sample sizes. The consequence of imposing different network structure on selection performance is further revealed by the two pathways analyzed in this work. Thus, our practical suggestion is to borrow available network information from well-known databases, especially when the sample size is small. In our real data analysis, we used the KEGG pathway information as prior knowledge to establish the graph structure. However, when such knowledge is not available, some statistical methods, such as the thresholding methods of Bickel and Levina (2008a; 2008b), Rothman et al. (2009), and Lam and Fan (2009), can be applied to estimate the network structure before applying our method. In addition, our current model was developed for continuous response. In human genetics, many disease responses are shown as binary variables. We plan to adapt our method to a generalized linear model framework in the future.