Augmentation of CBCT Reconstructed from Under-sampled Projections using Deep Learning

Abstract

Edges tend to be over-smoothed in total variation (TV) regularized under-sampled images. In this study, symmetric residual convolutional neural network (SR-CNN), a deep learning based model, was proposed to enhance the sharpness of edges and detailed anatomical structures in under-sampled CBCT. For training, CBCT images were reconstructed using TV based method from limited projections simulated from the ground truth CT, and were fed into SR-CNN, which was trained to learn a restoring pattern from under-sampled images to the ground truth. For testing, under-sampled CBCT was reconstructed using TV regularization and was then augmented by SR-CNN. Performance of SR-CNN was evaluated using phantom and patient images of various disease sites acquired at different institutions both qualitatively and quantitatively using structure similarity (SSIM) and Peak Signal-to-Noise Ratio (PSNR). SR-CNN substantially enhanced image details in the TV based CBCT across all experiments. In the patient study using real projections, SR-CNN augmented CBCT images reconstructed from as low as 120 half-fan projections to image quality comparable to the reference fully-sampled FDK reconstruction using 900 projections. In the tumor localization study, improvements in the tumor localization accuracy were made by the SR-CNN augmented images compared to the conventional FDK and TV based images. SR-CNN demonstrated robustness against noise levels and projection number reductions and generalization for various disease sites and datasets from different institutions. Overall, the SR-CNN based image augmentation technique was efficient and effective in considerably enhancing edges and anatomical structures in under-sampled 3D/4D-CBCT, which can be very valuable for image guided radiotherapy.

I. INTRODUCTION

According to the 2018 figures of American Cancer Society [1], lung and bronchus were estimated as the leading sites of new cancer deaths in the United States. Stereotactic body radiation therapy (SBRT) has emerged as an effective treatment technique of inoperable non-small cell early stage lung cancer [2–5]. SBRT uses high fractional dose and tight planning target volume (PTV) margin. Therefore, target localization accuracy is especially crucial for SBRT to achieve optimal local tumor control while minimizing radiation to surrounding healthy tissues. Due to the respiratory motion of the tumor in the lung, conventional three dimensional (3D-) cone-beam computed tomography (CBCT) is limited in localizing the moving target. Four dimensional (4D-) CBCT has been developed as a powerful tool to provide on-board 4D volumetric imaging for moving targets localization [6–8]. However, in 4D-CBCT, projection sampling for each respiratory phase is intrinsically sparse due to the scanning time and imaging dose constraint in clinical practice. From the under-sampled projections, the 4D-CBCT images reconstructed using the conventional Feldkamp–Davis–Kress (FDK) [9] method suffer from prominent noise and streak artifacts, adversely affecting the target localization accuracy. As a result, improving the quality of CBCT images reconstructed from under-sampled projections is essential for ensuring the precision of the radiation therapy delivery.

Different methods have been developed to improve the image quality of 4D-CBCT. Motion compensation and prior knowledge based estimation [10–14] were proposed to map 4D-CBCT at different phases onto a single phase through deformable registration during the iterations to compensate for the projection under sampling. Although image quality was improved, the deformable registration used in the reconstruction was time-consuming and prone to errors especially in the low contrast regions, leading to motion blurriness in the 4D-CBCT. Previously we have also developed a method to estimate 4D-CBCT based on prior images, deformation models and on-board limited projections [15–19]. The method effectively reconstructed high-quality 4D-CBCT images using limited projections acquired over a full or limited scan angle. However, as prior images and deformable registration were used in the method, the reconstruction was time-consuming and its accuracy was limited in the low contrast regions or anatomical regions that have large change from prior to on-board images.

Another category of methods includes iterative reconstruction (IR) algorithms based on the compressed sensing (CS) theory. Lp-norm (p ≈ 1.1) minimization based method developed by Li et al. [20] was successfully applied in blood vessel image reconstruction with 15 projections. Since the method was inherently utilizing the underlying image voxel sparsity in angiography, its applications in reconstructing more complex images were limited. Total variation (TV) and its variants [21–24] were then used as a regulation term to smooth out noise and streak artifacts. A TV based under-sampled image reconstruction algorithm, adaptive-steepest-descent (ASD)-projection-onto-convex-sets (POCS), was introduced by Sidky et al. [25] to improve the robustness against cone-beam artifacts. However, since the proposed approach utilized the globally-uniform TV penalization, anatomical edges were inevitably over-smoothed, adversely affecting the accuracy of tumor localization in image-guided radiation therapy. To alleviate over-smoothing, various edge-preserving methods have been developed. Edge guided TV minimization (EGTVM) was developed by Cai et al. [26] to address under-sampled computed tomography (CT) reconstruction. The proposed method introduced an iterative edge detection strategy to adjust the weights of TV regularization. Tian et al. [27] proposed edge-preserving TV (EPTV) for highly under-sampled CT reconstruction, where lower penalty weights were applied to the identified edges during iterations. Adaptive-weighted TV (AwTV)-POCS model presented by Liu et al. [28] took the anisotropic edge property into consideration and achieved better performance in preserving edge details. Lohvithee et al. [29] proposed the adaptive-weighted projection-controlled steepest descent (AwPCSD) method, which used AwTV in the steepest descent step and the results showed improvements in edge preserving. In these adaptive weighted TV methods, edge identification relies on applying specific manually designed edge detection strategies on the intermediate images reconstructed during the iterations. As a result, augmentation of the edges reconstructed from under-sampled projections is limited by the quality of the intermediate images, which is often blurred with losses of the edge information. Recently, we developed a prior contour based TV (PCTV) method to derive edge map from high-quality prior planning CT for edge enhancement in TV reconstructed images [30]. Specifically, prior CT was registered to the on-board CBCT through rigid or deformable registration. Based on the registration, edge information in the CT images were mapped to the CBCT to generate on-board edges, which were then used for edge enhancement in the reconstruction process. Results indicated the effectiveness of PCTV in edge preserving compared with EPTV. However, its performance was still limited by the accuracy and efficiency of the rigid or deformable registration between CT and CBCT.

In recent years, deep learning based methods have gained overwhelming attention in many image related tasks [31], ranging from high-level applications like segmentation [32, 33], classification [34] and detection [35] to low-level applications such as super resolution [36], image restoration [37], etc. Convolutional neural network (CNN) has been widely used in image reconstruction. Schlemper et al. [38, 39] introduced a deep cascading CNN based framework for under-sampled magnetic resonance imaging (MRI) reconstruction, which considerably accelerated the data acquisition of cardiac MRI. Han et al. [40] presented a deep U-Net architecture with residual learning for CS based CT reconstruction. Chen et al. [41] proposed a residual encoder-decoder convolutional neural network (RED-CNN) for low dose CT reconstruction. The presented method combined autoencoder, deconvolution network and shortcut connection, achieving a better performance than state-of-the-art methods. Kang et al. [42] developed a low dose CT denoising algorithm in wavelet domain based on CNN. Recently, Chen et al. [43] presented a deep learning based algorithm for statistical iterative CBCT reconstruction from fully-sampled projections. In their work, CNN was used to learn a potential regularization term from data, showing preferable image quality compared with TV and FDK. However, no studies on under-sampled CBCT reconstruction were performed in their work.

Considering the advantages of deep learning in image processing, we aim to explore the feasibility of using CNN to augment TV based under-sampled CBCT image quality in this study. The CNN proposed in our study consists of symmetrically stacked fully-connected convolutional layers, deconvolutional layers and residual connection, where the convolutional layers are for prominent feature extraction and deconvolutional layers are for the restoration of edge information and detailed anatomical structures. To the best of our knowledge, this is the first attempt to use deep learning to enhance edge information in TV regularized under-sampled CBCT images. The proposed method was evaluated using both an anthropomorphic digital phantom and real patient data. Results were evaluated both qualitatively and quantitatively demonstrating the effectiveness of the method in augmenting under-sampled CBCT image quality.

II. METHODS AND MATERIALS

A. Problem Formulation

Let x ∈ R^M×N represent the real-valued CBCT image composed of M×N pixels reconstructed from sparsely sampled projections, and y ∈ R^M×N represent the corresponding ground truth images which can be either CT or fully-sampled CBCT images. Then our problem can be described as finding a relationship between x and y so that

$$\text{arg}\underset{f}{\text{min}}\Vert f(x)-y{\Vert }_2^2$$ (1)

where f denotes the sophisticated image restoration process which can be estimated by CNN.

B. Overall workflow of CNN-based CBCT image quality augmentation

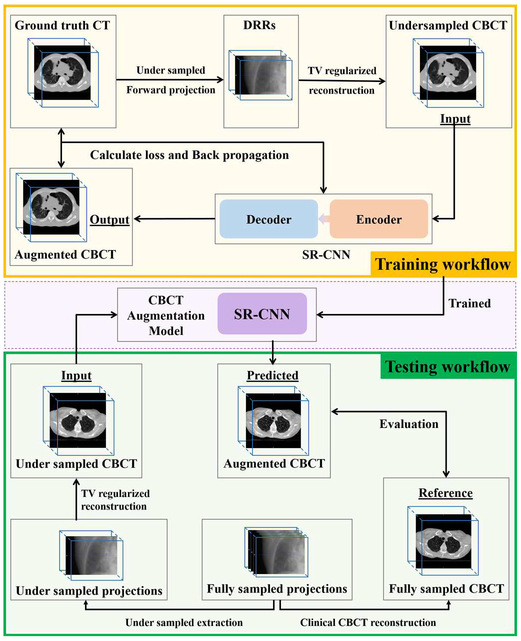
A deep learning based method proposed in our study aims to enhance the edge information in the TV-minimized CBCT images. CNN is applied to find a relationship between under-sampled CBCT and fully-sampled CBCT or CT images. The general workflow is shown in Fig. 1. In the training workflow, patient CT images were used as the ground truth images. Under-sampled projections were simulated from the ground truth volume based on the cone-beam half-fan geometry with a uniform distribution over a 360° scan angle. CBCT was then reconstructed from under-sampled projections using the ASD-POCS TV algorithm proposed by Sidky and Pan’s method [25]. 40 iterations were used in the reconstruction with parameters of line-search, alpha and epsilon empirically-tuned. All TV based reconstruction is implemented and performed in Matlab 2018a. The reconstructed under-sampled CBCT was used as input to the proposed symmetric residual convolution neural network (SR-CNN), which was trained to generate augmented CBCT images to match with the ground truth images. The details of the SR-CNN are described in Section C.1.

Fig. 1.

General workflow of symmetric residual convolution neural network (SR-CNN). Yellow box indicates network training workflow. Green box indicates network testing workflow.

Once weights in the network are determined, various data are used in the testing workflow to evaluate the network’s performance to augment under-sampled CBCT image quality. In brief, under-sampled projections were retrospectively extracted from patients’ fully-sampled projection data, and were used to reconstruct under-sampled CBCT using the ASD-POCS TV based iterative method. SR-CNN was then used to predict augmented CBCT image based on the under-sampled CBCT. The fully-sampled CBCT was used as a reference to evaluate the augmented under-sampled CBCT.

C. Symmetric Residual Convolution Neural Network (SR-CNN)

1). Network Architecture

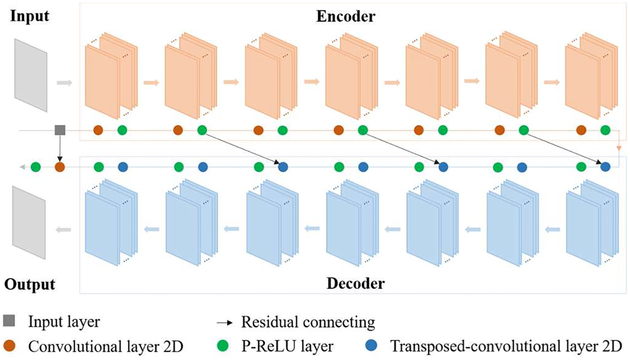
In this study, chained fully-connected convolutional layers are applied to extract feature patterns from input images, and symmetrically stacked fully-connected deconvolutional layers are used to restore images from activation maps. Here by symmetric, we mean not only the same number of layers in encoder and decoder, but also the same filter number, filter size, stride and zero-padding policy of mirrored layers. Parametric rectified linear unit (P-ReLU) layer comes after each convolutional or deconvolutional layer to introduce nonlinearity to the network. Neither pooling nor up-pooling layer is applied in our network for detail reservation which is essential for our task. The image processing is constrained to the image domain.

An overall architecture of our network is illustrated in Fig. 2. It contains symmetric convolutional and deconvolutional layers in encoder and decoder with residual addition connection, and one convolutional layer following the decoder for the output. Image restoration is a low-level task which is supposed to require a relatively shallow network for detail preservation. However, compared with deeper network, expressing capability of shallower network is limited to describe complicated relationship between the input and output. Deep residual learning was first proposed to avoid the degradation problem when network grew deeper [44]. As a result, residual connections are introduced to our network to achieve a better balance between network depth and performance. The network can be formulated as follows:

• for encoder:

  $$\begin{gathered} C_i=\text{ PReLU }\left(W_{ij}\otimes C_{i-1}+b_{ij}\right) \\ i=1,2,\dots ,L,\text{ and }j=1,2,\dots ,F \end{gathered}$$ (2)
• for decoder:

  $$\begin{gathered} T{C}_m=\{\begin{array}{ll}\text{PReLU}\left(W_{m,n}{\otimes }^T\left(T{C}_{m-1}+C_{L-m+1}\right)+b_{m,n}\right),\hfill & \hfill ifresidualconnecting\\ \text{PReLU}\left(W_{m,n}{\otimes }^{T}T{C}_{m-1}+b_{m,n}\right)\hfill & \hfill else\end{array} \\ m=1,2,\dots ,L,\text{ and }n=1,2,\dots ,F \end{gathered}$$ (3)
• for output:

  $$O=\text{PReLU}\left(W_o*T{C}_L+b_o\right)$$ (4)

  and

  $$PReLU(x)=\{\begin{array}{l}x,\text{ if }x>0\hfill \\ p*x,else\hfill \end{array}$$ (5)

  where C_i is the output of the convolution unit (including a convolutional layer followed by a P-ReLU layer) except that C₀ is the network input, TC_m is the output of deconvolution unit (including a deconvolutional layer followed by a P-ReLU layer) except that TC₀ equals to C_L which is the output of the encoder, ⊗ represents the convolution operator, ⊗^T represents the deconvolution operator, W is the weights of each filter in every layer, b is the bias associated with each corresponding filter, L is the number of convolution or deconvolution units, F is the filter number in each convolutional or deconvolutional layer, and p is a learnable parameter for each input pixel of P-ReLU layer.

Fig. 2.

Overall architecture of symmetric residual convolution neural network (SR-CNN).

Three major modifications are made compared with the network proposed by Chen et al [41]. First, the encoder has a symmetric architecture with the decoder. An additional convolutional layer followed the decoder is used to keep the output dimension same as the ground truth. Second, P-ReLU layer is applied in the network instead of ReLU to avoid dead ReLU problem in some extreme situations as well as to pose less positivity constraint to feature maps to potentially improve the image contrast. Third, difference of structural similarity index matrix (SSIM) is used as loss function instead of mean squared error (MSE). Pixel-wise MSE tends to over-smooth edge information [45, 46] and is poorly correlated with human perception of visual system. Images with same MSE may have various distortions or noise. In contrast, SSIM has been demonstrated to show more information about structure similarities [47].

2). Patch Extraction

Large training dataset is usually required for deep learning. Insufficient training samples tend to overfit the network, meaning that the network can well predict training data while poorly predict data that is not in the training dataset. However, for CT image, it’s challenging to accumulate the large number of slices required for sufficient sampling. To resolve this, the strategy of extracting overlapped patches from CT images was used in this study to increase the training samples. This patch based approach has been proven to be efficient and effective in previous studies [36, 37, 41]. The patch size was set to 50 by 50 with a stride of 5, resulting in 1.3×10⁶ training patch pairs. No data augmentation technologies, such as translation, rotation, flipping or scaling, were applied in this study.

3). Network Compilation and Fitting

The network proposed in our study is an end-to-end mapping from the patches of the under-sampled CBCT image to those of the corresponding fully-sampled CBCT. Parameters in the convolutional and deconvolutional filters as well as the P-ReLUs are estimated by minimizing the loss function. Given training sample set of paired patches P = {(x₁, y₁), (x₂, y₂), …, (x_N, y_N)} where x_i and y_i are the corresponding patches of under-sampled and fully-sampled CBCT images respectively and N is the number of training samples, the loss function of structural dissimilarity in each forward-backpropagation is defined as

$$L(D;\Theta )=\frac{1}{M}{\sum }_{i=1}^M\frac{1}{2}\left(1-SSI{M}_i\right)$$ (6)

$$SSIM=\frac{\left(2{\mu }_x{\mu }_y+C1\right)\left(2{\sigma }_{xy}+C2\right)}{\left({\mu }_x^2+{\mu }_y^2+C1\right)\left({\sigma }_x^2+{\sigma }_y^2+c2\right)}$$ (7)

where D is the training data, Θ is the network weights, M is the batch size of the network for loss backpropagation, μ_x and μ_y are the average of the patch pair (x, y), σ_x and σ_y are the variance, and C1 and C2 are hyper-parameters. In our study, M is 10, SSIM is calculated on window sizes of 3 by 3, C1 equals to (0.01×2000)² and C2 equals to (0.03×2000)² where 2000 is the maximum intensity of our ground truth. Loss function L(D; Θ) is optimized by stochastic gradient descent (SGD). Learning rate is 0.01, and learning decay is 0.

D. Experiment Design

1). Model Training and Validation Data

4D CTs of 11 patients with lung cancers were randomly chosen from the AAPM “Sparse-view Reconstruction Challenge for Four-dimensional Cone-beam CT (4D CBCT)” (SPARE Challenge) in our study for model training. One phase of the 4D-CT of each patient was selected for the study. Breath hold CT volumes from 5 lung cancer patients acquired at our institution were used as the validation data, which helped tuning the SR-CNN hyper-parameters including the filter number and filter size in each layer, and the number of layer in the encoder/decoder.

CT volumes served as the ground truth. Under-sampled CBCT images were reconstructed with the ASD-POCS TV method from 72 uniformly distributed noise-free cone-beam half-fan digitally reconstructed radiographs (DRRs) that were simulated from the ground truth CT volume data. Projection matrix size was 512×384 with pixel size of 0.776mm×0.776mm, matching with the typical size and resolution of projections used for clinical CBCT reconstruction. Source-to-ioscenter distance was 100cm, and source-to-detector distance was 150cm. The detector was shifted 14.8cm for half-fan projection acquisition.

In order to balance between image resolution and computing resource, all CT and CBCT image data were set to have a volume of 300×300×150 voxels with voxel size of 1.5mm×1.5mm×1.5mm.

2). Model Hyper-parameter Configuration

In this study, we conducted experiments on different hyper-parameter combinations to study the relationship between the network’s hyper-parameters and its performance.

Filter number was set to 16, 32, 64 and 96, and filter size was set to 3 and 5 to study the relationship between the filter dimension and the model performance. Using the optimized filter number and size, number of layers in the encoder and decoder was set to 3, 5, 7 and 9 to investigate how the network depth influenced the performance.

Besides the hyper-parameters mentioned above, filter number of the output convolutional layer was set to 1 to keep the output image dimension same as the ground truth. Filters were initialized with random Gaussian distribution with 0 mean and 0.05 standard deviation. Convolution and deconvolution stride was set to 1 with zero padding.

Models of different hyper-parameters were evaluated using the validation data. As mentioned in Section D.1., the validation data were collected under an IRB approved protocol from 5 breath hold lung CT volumes containing 400 slices scanned at our institution. The body region covering the full body was used to evaluate the overall model augmentation while excluding the couch and background noise.

Model-enhanced image quality was evaluated in a quantitative way using Peak Signal-to-Noise Ratio (PSNR) and SSIM. SSIM is defined in (7) and PSNR is formulated as follows:

$$\text{MSE}=\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2$$ (8)

$$\text{PSNR}=10\times lo{g}_{10}\left(\frac{MA{X}_y^2}{MSE}\right)$$ (9)

where n is number of pixels, y_i and ${\widehat{y}}_i$ are intensities of pixel i in the ground truth and augmented CBCT image, respectively, and MAX_y is the maximum value of the ground truth image.

Model of the hyper-parameters presenting the best performance was used for the following evaluation studies.

3). Model Evaluation

Once the model hyper-parameters were determined and the weights were settled, performance of the trained model was evaluated using phantom, simulated DRRs and real clinical projection data. No re-training for the model was conducted when the model addressed different reconstruction conditions and disease sites.

a). Phantom Data Study

The extended cardiac-torso (XCAT) phantom includes detailed and realistic anatomical structures. Onboard ground truth images and CBCT projections were simulated with XCAT. To validate the robustness of the network against noise, different levels of noise with Poisson and normal distribution were incorporated in the simulated DRRs following the equation [17]

$$Noise(i,j)=-\text{ln}\left(\frac{Poisson\left(I_0{e}^{-P(i,j)}\right)+Normal\left(0,{\sigma }^2\right)}{I_0}\right)$$ (10)

Noise was added to DRRs in a pixel-wise method. I and j denote the index of pixel in projection. I₀ was set to 10⁵, indicating the intensity of incident photons. σ² is the variation level of normal distribution, and was set to 0, 10, 50 and 100 to simulate different noise levels.

b). Patient Study using Simulated Projections

Breath hold CT volumes of five lung patients and four liver patients acquired at our institution were included in this study to evaluate the model performance in CBCT augmentation as well as the model robustness against different disease sites. Note that the five lung patients in this study were not included in the validation dataset. In addition, 4D CT volumes of another five lung patients from the TCIA 4D-Lung dataset [48, 49] were also included in this study to evaluate the model robustness against various input image qualities from different institutions. One phase of the 4D CT of each patient was selected for the study.

The under-sampled CBCT images were reconstructed from 72 half-fan simulated projections using the ASD-POCS TV method. Parameters for DRR simulation are the same as described in Section II.D.1. The corresponding CT volumes were used as the ground truth.

In this study, two ROIs were used to evaluate the result. One is the body region, and the other is the planning target volume (PTV). PTV for breath hold lung and liver volumes were drawn by physicians at our institution, and PTV for 4D lung volumes were provided by the TCIA 4D-Lung dataset.

c). Patient Study using Real Cone-beam Projections

A set of 4D CBCT projections from the SPARE Varian dataset was randomly selected in this study to show the ability of the network in handling respiratory motion. The CBCT projections were acquired from a Varian Clinac for research purpose. In this dataset, 145 respiratory cycles appeared in the 4D CBCT scanning, and one projection of phase 6 was extracted from each respiratory cycle. As a result, a subset containing 145 half-fan projections was used for the under-sampled image reconstruction. The FDK images reconstructed from all the 224 projections of phase 6 using ramp filter were used as the reference.

The projections in each phase of the 4D CBCT is intrinsically sparse, thus the reference FDK images reconstructed from 224 projections still suffer from severe streaks and noise. Therefore, there is no high quality ground truth images available to quantitatively evaluate the augmented images. To address this, we used another set of breath-hold CBCT projections from a lung cancer patient scanned in our institution to quantitatively evaluate the performance of the network in enhancing edge details for clinical cases. The CBCT projections were acquired by the TrueBeam (Varian Medical Systems, Inc., Palo Alto, CA) using 20 mA and 15 ms and extracted under an IRB-approved protocol. Projection matrix size is 512×384 with pixel size of 0.776mm×0.776mm. Source-to-ioscenter distance is 100cm, and source-to-detector distance is 150cm. The detector was shifted 16.0cm for half-fan projection acquisition. Ground truth CBCT images were reconstructed by a clinical CBCT constructor using full-sampling acquisition of 895 projections. Under-sampled CBCT images were reconstructed from a subset of fully-sampled projections. In this study, various projection numbers of 90, 120 and 180 were used to evaluate the robustness of the method against different under sampling schemes.

4). Comparison with State-of-the-Art CNN architecture

Performance of our proposed SR-CNN was compared with three different state-of-the-art CNN architectures including encoder-decoder (RED-CNN) [41], simple stacked CNN (Super Resolution CNN) [36] and U-Net based denoising network (KAIST-CNN) [40]. RED-CNN employed an asymmetric encoder-decoder architecture with residual connection, and was proposed to enhance the low dose CT image quality in the image domain. Here we called the RED-CNN an asymmetric encoder-decoder architecture because the filter number in the first layer of encoder is different from that in the last layer of decoder. Super Resolution CNN used a succinct three-layer CNN with carefully-tuned hyper-parameters to learn an end-to-end mapping from low to high resolution images. KAIST-CNN was developed based on U-Net to augment CS CT image quality using residual learning. All the network settings were configured following the suggestions proposed in the original papers, and were trained on the same training dataset as mentioned in Section II.D.1.

5). Image Quality Evaluation Metrics

SR-CNN augmented CBCT images were compared with corresponding ground truth images in both qualitative and quantitative ways. Visual check focused on image edge details such as bone edges or lung vessels. And two commonly used metrics, PSNR and SSIM, were used for quantitative evaluation within body and PTV regions. SSIM is defined in (7), and PSNR is defined in (9).

6). Tumor Localization Evaluation

To evaluate the performance of the proposed model using a task related metric, we enrolled lung cancer SBRT patients treated with breath-hold and scanned with full sampling 3D CBCT, and evaluated the tumor localization accuracy using the augmented images.

In total, 11 patients with 39 CBCT scans (2–5 daily CBCTs per patient) were collected from lung SBRT patients treated at our institution under an IRB-approved protocol. Among them, 7 patients had real CBCT projection data available at the time of collection. The CBCT acquisition was the same as the breath hold lung patient mentioned in Section II.D.3.c. For the under-sampled CBCT reconstruction, 128 projections were extracted from the fully-sampled projection set (around 900 projections) according to the angles of a typical 4D CBCT scan. The other 4 patients did not have the projection data available due to the limited storage time at the linear accelerator (LINAC) machine. For them, 72 DRRs were simulated from the fully-sampled CBCT volumes and were used as the projection subset for reconstruction. The DRR simulation process was same as what mentioned in Section II.D.1.

For every fraction of each patient, under-sampled FDK was reconstructed from the projection subset using the ramp filter. Under-sampled TV images were reconstructed from the same projection subset using the ASD-POCS TV method. And then the TV images were fed into the trained SR-CNN for augmentation. Fully-sampled CBCT were reconstructed using a clinical constructor with the full sampling projections and were used as a reference.

To evaluate the accuracy of the reconstructed under-sampled CBCT images for target localization, rigid registration was performed by the clinician between planning CT and the reconstructed under-sampled CBCT images to determine the patient positioning shifts, which were then compared to the patient shifts determined from the reference fully-sampled CBCT images to evaluate their accuracy.

III. RESULTS

A. Model Hyper-parameter Configuration

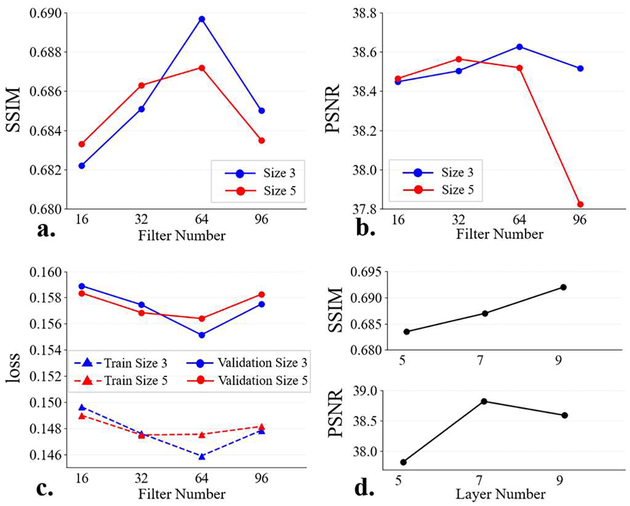
Fig. 3 shows the SSIM and PSNR results of the validation data.

Fig. 3.

Results of the SR-CNN hyper-parameter configuration. (a) is the SSIM as a function of filter number, (b) is the PSNR as a function of filter number, (c) is the training and validation loss as functions of filter number, and (d) is the SSIM and PSNR as functions of layer number in the encoder/decoder.

1). Filter Number and Filter Size

In this section, layer number of the encoder/decoder was set to 5. Firstly, the filter size is fixed to (3, 3). Fig. 3(a-b) show that the SSIM and PSNR increase with the filter number from 16 to 64 and decline from 64 to 96. When the filter size is enlarged from (3, 3) to (5, 5), performance degrades for a relatively wide SR-CNN (64- and 96-filter). Fig. 3(c) indicates that the model training error presents a similar trend to the validation error, demonstrating it is not the overfitting that leads to the model performance decline. In an overfitting case, training error gets smaller while validation error increases.

As a result, the best performance was achieved by a SR-CNN with 64 filters in each layer and the filter size of (3, 3).

2). Layer Number of the Encoder/Decoder

In this section, filter number was set to 64 and filter size was set to (3, 3) based on the results of Section III.A.1. Fig. 3(d) shows that model performance improves when number of layer in encoder/decoder increases from 5 to 7, and SSIM keeps increasing from 7 to 9 while PSNR drops. As a result, the encoder/decoder depth was set to 7.

B. Model Evaluation

1). Phantom Data Study

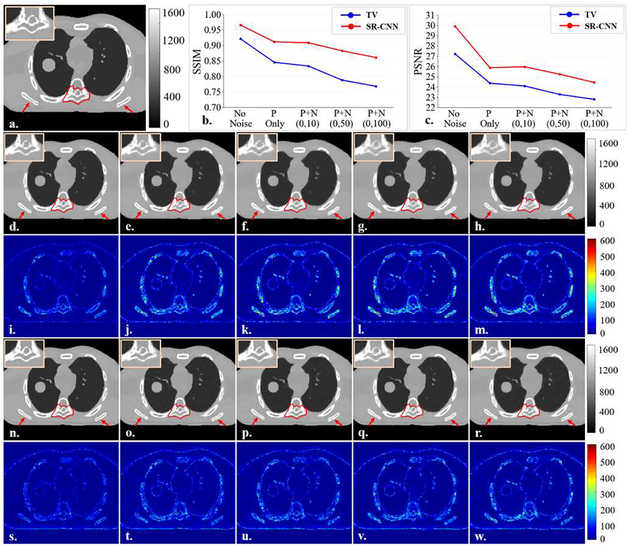
Fig. 4 shows the results of SR-CNN augmentation for different noise levels in the projection images in the XCAT study. Fig. 4(b) and (c) show the SSIM and PSNR of ROIs in the under-sampled TV based CBCT and SR-CNN augmented CBCT for different noise levels. Results demonstrated that although both TV and SR-CNN based CBCTs had degraded image quality as noise level increased, SR-CNN always achieved higher SSIM and PSNR than TV method. In addition, compared to TV method, SR-CNN well enhanced images details, particularly the bone edges, in all levels of noisy cases, as shown in the image comparisons.

Fig. 4.

Results of noise study on XCAT. A free-shape region of interest (ROI) is highlighted in red contour in the vertebra body to evaluate our proposed SR-CNNhi robustness against noise. (a) is onboard ground truth CBCT image simulated with XCAT. (b-c) are the SSIM and PSNR of selected ROI as functions of noise level in 72 XCAT-simulated cone-beam half-fan projections. P in x-axis label indicates Poisson noise and N indicates Normal distribution noise. (d-h) are TV-minimization reconstructed images from projections of different noise levels (same order with (b) and (c)). (i-m) are the corresponding difference images between (d-h) and the ground truth. (n-r) are (d-h)sponding difference images between (d-h) and the ground tru corresponding difference images between (n-r) and the ground truth. ROIs are zoomed in and placed on the upper left corners of images. Red arrows indicate image details for visual inspection. Color bar in each column indicates the image display window/level.

2). Patient Study using Simulated Projections

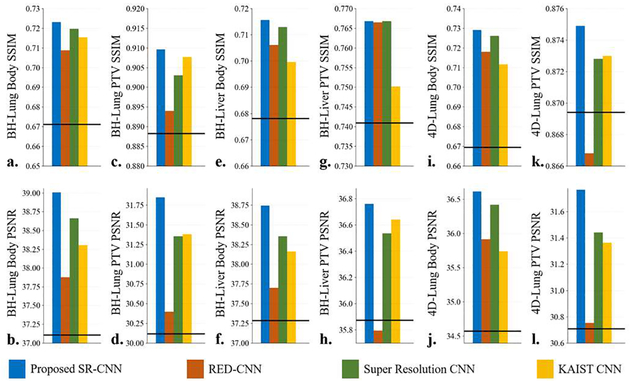
Under-sampled CBCT images were reconstructed with TV regularization using 72 uniformly-distributed DRRs over 360 degrees. And then the TV-based images were fed into our proposed SR-CNN as well as three other CNNs mentioned in Section II.D.4 for comparison. Fig. 5A shows the quantitative results of the under-sampled image augmentation. Horizontal line in each figure indicates the input TV-regularized image metric. All the CNNs demonstrated improvement compared with the input TV images except for the RED-CNN in breath hold liver PTV and in 4D-Lung PTV (Fig. 5A.h and Fig.5A.k). And our proposed SR-CNN outperformed the other three CNNs in both body and PTV on all testing datasets, indicating SR-CNN’s robustness against disease sites, projection quality as well as input image quality.

Fig. 5A.

Quantitative results of the study on reconstruction using projections simulated from real patient data with lung and liver tumor and from different institutions. (a-b) are the mean SSIM and PSNR within body region of the breath hold lung patients. (c-d) are the mean SSIM and PSNR within PTV of the breath hold lung patients. (e-f) are the mean SSIM and PSNR within body region of the breath hold liver patients. (g-h) are the mean SSIM and PSNR within PTV of the breath hold liver patients. (i-j) are the mean SSIM and PSNR within body region of the 4D Lung patients. (k-l) are the mean SSIM and PSNR within PTV of the 4D Lung patients. The horizontal line in each figure indicates the input TV image metric.

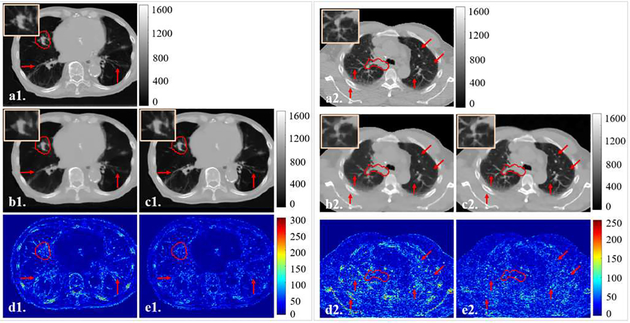
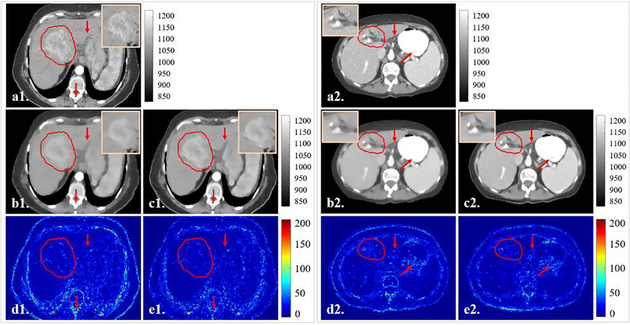
Fig. 5B are two representative slices from the breath-hold lung dataset and the 4D-Lung dataset. Results indicated that the ASD-POCS TV method was able to remove noise and streaks with compromised edge information when reconstructing CBCT images using under-sampled projections. SR-CNN enhanced the bone edges as well as the small lung structures which were blurred in the input TV-based images. Fig. 5C are two representative slices from the breath-hold liver dataset. Compared to the input TV-based images, liver boundaries and tumor PTV edges were augmented by our proposed SR-CNN in both high contrast and low contrast regions.

Fig. 5B.

Representative slices in the (1) breath hold lung and (2) 4D-Lung testing dataset for the patient simulated projections study. Clinical PTV ROI is highlighted in red contour, and ROIs are zoomed in and placed on the upper corners of images. (a) is the ground truth CT slice, (b) is the TV image, and (c) is our proposed SR-CNN augmented image. (d-e) are the corresponding difference images between (b-c) and the ground truth. Red arrows indicate image details for visual inspection. Color bar in each column indicates the image display window/level.

Fig. 5C.

Representative slices in the breath hold liver testing dataset for the patient simulated projections study. Clinical PTV ROI is highlighted in red contours, and ROIs are zoomed in and placed on the upper corners of images. (a) is the ground truth CT slice, (b) is the TV image, and (c) is our proposed SR-CNN augmented image. (d-e) are the corresponding difference images between (b-c) and the ground truth. Red arrows indicate image details for visual inspection. Color bar in each column indicates the image display window/level.

3). Patient Study using Real CBCT Projections

a). Evaluation of SR-CNN using Real 4D-CBCT Projections

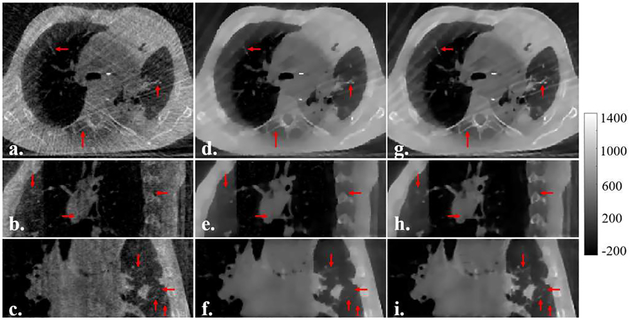
A subset containing 145 projections was extracted from one phase of a SPARE Varian 4D CBCT scanning, and was used for the under-sampled TV-regularized image reconstruction. Fig. 6A shows the qualitative comparison between the referenced FDK-based, under-sampled TV-based and SR-CNN augmented images. SR-CNN augmented images present much less streaks and better image contrast compared to the referenced FDK-based images, and much sharper edges of bones and small lung structures compared to the TV-based images.

Fig. 6A.

Results of SR-CNNar in each column indicates the image displ are the referenced fully-sampled FDK images reconstructed from 224 projections. (d-f) are the under-sampled TV images reconstructed from 145 projections. (g-i) are the SR-CNN augmented images. Color bar on the right side indicates the image display window/level.

The FDK image reconstructed from the fully-sampled projections of one phase is the best reference we can get in clinical practice, but it’s still of poor image quality. In consequence, no quantitative evaluation was conducted in this study.

b). Evaluation of SR-CNN Robustness against Projection Number using Real Breath-hold CBCT Projections

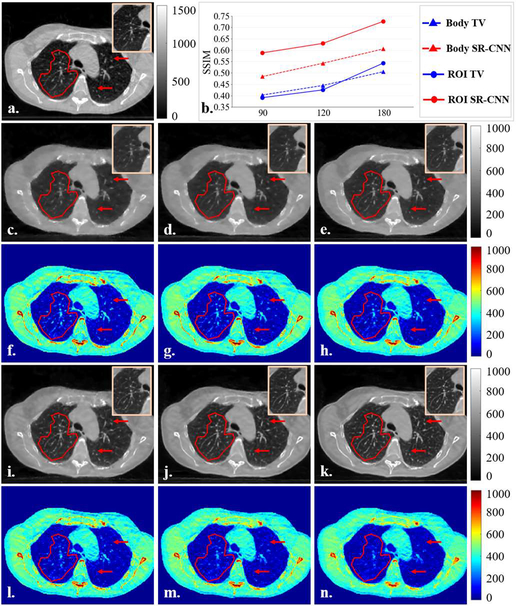
TV based CBCT images were reconstructed using under-sampled projections uniformly extracted from the fully-sampled half-fan projections acquired for a clinical breath-hold lung cancer patient at our institution. Different numbers of projections were used for the under-sampled image reconstruction to evaluate the robustness of the SR-CNN augmentation against projection number reductions. In Fig. 6B, a representative ROI was selected to verify the performance of SR-CNN for augmenting CBCT reconstructed from different numbers of clinical projections. SR-CNN demonstrated substantial enhancement of anatomical details such as lung vessels and bone edges compared to TV based images for all projection number scenarios. Quantitative analysis is plotted in Fig. 6B(b). Although both TV and SR-CNN had degraded SSIM when projection number was reduced, SR-CNN always outperformed TV at all levels in both ROI and whole body.

Fig. 6B.

Results of SR-CNN robustness study. A free-shape region of interest (ROI) is highlighted in transparent red mask to evaluate our proposed SR-CNNI) robustness against clinical projection number. (a) is ground truth CBCT image reconstructed from fully-sampled projections using a clinical CBCT constructor. (b) is the SSIM of selected ROI as function of projection number. (c-e) are TV based CBCT images reconstructed from 90, 120 and 180 projections, respectively. (f-h) are the corresponding difference images between (c-e) and the ground truth. (i-k) are corresponding SR-CNN augmented images. (l-n) are the corresponding difference images between (i-k) and the ground truth. ROIs are zoomed in and placed on the top corners of images. Red arrows indicate image details for visual inspection. Color bar in each column indicates the image display window/level.

4). Tumor Localization Evaluation

The localization accuracy of different methods was shown in the Table I. Compared with under-sampled FDK and TV, results showed that the SR-CNN effectively reduced the localization errors by over 50% in all directions compared to the FDK and TV only methods. Especially, the maximum vector length of the 3D localization errors was reduced from 3.5 mm and 3.6 mm for FDK and TV methods to 1.4 mm for TV+SR-CNN.

Table I.

Tumor Localization Results

Methoda	Directionb	Tumor Localization Errorc
FDK	x	1.2 ± 0.4 (0.4, 2.0)
	y	1.2 ± 0.4 (0.1, 2.3)
	z	1.5 ± 0.4 (0.7, 2.5)
	d	2.3 ± 0.5 (1.5,3.5)
TV	x	1.1 ± 0.3 (0.4, 1.7)
	y	1.2 ± 0.4 (0.5, 2.0)
	z	1.5 ± 0.4 (0.8, 3.1)
	d	2.3 ± 0.4 (1.5, 3.6)
TV+SR-CNN	x	0.4 ± 0.3 (0.0, 1.0)
	y	0.5 ± 0.3 (0.0, 1.0)
	z	0.7 ± 0.3 (0.1, 1.1)
	d	1.1 ± 0.2 (0.4, 1.4)

^aFDK is the under-sampled image reconstructed using FDK with ramp filter, TV is the under-sampled image reconstructed using TV regularization, and SR-CNN is the augmented TV image using the proposed SR-CNN.

^bx is the left-right (LR) direction, y is the anterior-posterior (AP) direction, z is the superior-inferior (SI) direction, and d is the 3D vector length of the errors.

^ctumor shift unit is millimeter (mm). The results are presented in mean ± standard deviation of the absolute errors, and the minimum and maximum absolute errors are listed in the brackets.

IV. DISCUSSION

Improving CBCT reconstruction from under-sampled projections is important in clinical practice. For example, for better tumor localization, it is essential to improve the quality of 4D-CBCT reconstruction, which uses intrinsically sparse projections in each respiratory phase. Moreover, for 3D CBCT reconstruction, reducing projections is an effective way to reduce on-board imaging dose, which is a major clinical concern when repetitive CBCT scans are acquired for inter- or intra-fraction verification [50, 51]. In view of them, SR-CNN, a deep learning based model, was proposed in this study to enhance the quality of under-sampled CBCT reconstruction. It takes the advantages of TV regularization to suppress noise and streak artifacts. Meanwhile, instead of the manually designing an edge-preserving strategy in previous adaptive TV methods [26–30], SR-CNN learns a sophisticated restoring pattern from the training data to generate a fast and effective approach to enhance the edge or detailed information in CBCT. Our proposed model achieves excellent performance in enhancing details such as small lung structures and bone edges with quality close to the fully-sampled CBCT, as demonstrated in the various experiments in this study. Improvement in tumor localization accuracy was made by the SR-CNN augmented 4D-CBCT images compared with traditional FDK- and TV-based reconstruction.

To explore the relationship between network hyper-parameter configuration and model performance, different hyper-parameter combinations were evaluated in our study. Body region containing full body while excluding couch and background noise was used to evaluate the overall enhancement achieved by the trained model. Results indicated that smaller filters (3×3) worked better in relatively wide network consisting of 64- or 96-filter layers. As is known to us that CNN works on two assumptions. One is that the features are local, and the other is that the feature which is useful in one part is also useful in other parts. So filter size is determined by how locally the feature is useful in the specific task. And the network width, or the filter number in each layer, determines how many types of features to be extracted. For the task of under-sampled CBCT image augmentation, each pixel is related to the very neighboring pixels. And due to the complex structures and contrast in the CBCT images, large number of features are expected to be detected. As a result, a wide network with smaller filters is desired, which is in accordance with our result. However, it is not always the case that more filters contribute to better performance. A turning point is observed when filter number increases. Model performance is getting better before the turning point and is getting worse after the turning point. But the network performance degradation is not caused by the overfitting. It can be told from the result that adding more filters to a suitably wide network, 64 filters per layer in our case, also leads to higher training error (DSSIM) on training dataset. Such degradation may result from the overkilling on the training data due to the large amount of learnable weights in network. Though previous experience may suggest that wide network could capture richer features to improve the network accuracy, our study demonstrated that too wide network could also suffer from the performance degradation. As for the network depth, deeper network showed improved performance because more convolutional and non-linear operations can increase the representation capability and enlarge the reception field, thus leads to better traction on data. Yet near neighboring pixels are much more important than the far neighboring ones. Thus a suitably deep network can hardly benefit from more layers. And as observed in previous works [36, 44, 52], performance degradation also showed up in our study when network kept growing deeper.

All the network training and evaluation were implemented in Python with Keras framework using TensorFlow backend, and were performed on a PC (Intel Xeon CPU, 32 GB RAM, GTX1080 GPU with 12 GB memory). Training for the configured network took about 2.25 hours for each epoch, and in our study, epoch number was empirically set to 10. The SR-CNN prediction itself took about 0.12 second for each slice with dimension of 225 by 200 and around 18 seconds for 150 slices, making the method very practical for clinical implementation.

Our studies demonstrated the robustness of the SR-CNN against noise levels and projection number reductions. SR-CNN consistently outperformed TV method across all scenarios. Furthermore, it’s worthy to mention that the model was trained using patients CT and simulated projection data acquired at one institution and tested using phantom, different patients with simulated and real projections acquired at various institutions, which demonstrated the generalization of the model for CBCT image quality under different clinical scenarios.

Also, the model trained on the high contrast lung region data performed well on the low contrast liver region, indicating its generalizing ability across various disease sites. An overall outperformance over the three other state-of-the-art CNN architectures showed the effectiveness of our proposed SR-CNN.

In the training process, CT images were used as the ground-truth images instead of fully-sampled CBCT reconstructed using the FDK method for the model training. This is because the fully-sampled FDK based CBCT image suffers from cone-beam artifacts and HU inaccuracies. Therefore, CT was used in our study as the target for learning to augment under-sampled CBCT images. Because the under-sampled CBCT used for the network training was reconstructed from DRRs of the CT images, the SR-CNN model was trained to reduce the blurriness caused by under sampling, TV reconstruction and cone-beam non-uniform sampling.

Note that in the patient study using real CBCT projections for testing, we would need to establish a ground truth to compare and determine the localization accuracy of clinical 4D-CBCT before and after the augmentation. Typical clinical 4D-CBCT scans have limited projections for each respiratory phase, and the FDK-based image quality is far from enough to be used as the ground truth for the evaluation. One option to establish the ground truth images is to acquire sufficient projections, e.g. around 600 projections, for each respiratory phase in the 4D-CBCT scan to reconstruct high quality images as the reference. However, this will substantially increase the scanning time and imaging dose of the 4D-CBCT scan, making it challenging or impractical to enroll patients under the current clinical workflow. As an alternative, we used real on-board projections of breath hold 3D CBCT scans of the lung patients. Since patients held breath during the CBCT scan with minimal respiratory motion, 3D CBCT scan is typically acquired with around 900 projections in clinical practice, which are sufficient to establish the high-quality images as the ground truth. Under sampled projections were retrospectively extracted from the 900 projections to mimic the 4D-CBCT acquisition at the breath-hold phase.

Tumor localization accuracy is crucial in SBRT. This preliminary study showed that the image quality improvement made by the proposed SR-CNN improved localization accuracy using CBCT. The maximum vector length of the 3D localization errors was considerably reduced from over 3.5 mm for FDK and TV method to 1.4 mm for TV+SR-CNN, which is clinically significant considering the tight PTV margin as small as 3mm used in lung SBRT treatments to account for localization errors. This over 50% reduction of the localization errors by the SR-CNN can lead to improvement of the coverage of the tumor during the localization process, which is directly correlated to the tumor control in SBRT. In this study, to comply with the clinical practice for lung tumor localization based on the CBCT, manual registration was used instead of automated registration. Yet one observer may introduce bias in the results, and comprehensive evaluations involving more observers are desired in the future study to reduce the uncertainties.

It is worth noting that, as a post-processing model, the proposed SR-CNN is incapable of creating details out of nothing. When the projection number is extremely low and the details are slightly distorted or completely lost in TV based images, the augmentation achieved by our proposed model is limited. In this study, we reconstructed CBCT images of lung using as low as 120 half-fan on-board projections and achieved comparable image quality with even sharper edges in the lung relative to the fully-sampled FDK reconstruction with ramp filter using 900 projections. Note that using different filters may affect the sharpness of the structures in the reference CBCT data. In this study, all the FDK images were reconstructed using the ramp filter which is commonly used in clinical CBCT constructors.

Another option for the SR-CNN augmentation is to augment the FDK images typically used in clinical practice. However, if the projection data are under-sampled, the quality of FDK images are severely limited by streak artifacts, which affected the quality of the augmented images afterwards. In regions with heavy streaks in the FDK images, the SR-CNN cannot fully differentiate streaks from real anatomy edges. Consequently, it may remove anatomy edges as streaks or enhance streaks as edges, causing inaccuracies in the reconstruction. Starting with TV based images give us a much better starting image with much less artifacts than FDK based images, and as a result it leads to a better image after the augmentation.

In this study, parameters for TV based reconstruction were empirically tuned to tradeoff between de-noising and deblurring. In the 4D-CBCT augmentation study, in order to preserve details, the ASD-POCS TV couldn’t completely remove all streaks due to the projection number and dose level. Yet the SR-CNN didn’t learn to deal with such streaks during the training. Thus the model treated the streaks as edges to be augmented. The performance of the SR-CNN can further benefit from the improvements in TV based reconstruction. In future studies, our proposed SR-CNN can be incorporated with other image reconstruction methods for image augmentation, such as enhancing EPTV or PCTV based images for a better detail augmentation. Motion modeling and prior information based 4D-CBCT reconstruction techniques can also be incorporated in our workflow to get further enhancement in image quality. Also, 3D CNN can also be studied to explore 3D context information for better augmentation, but the tradeoff between performance and computing resource needs be considered. In addition, our model can be trained on clinical onboard projections and learns an end-to-end map from under-sampled CBCT to corresponding registered CT images to augment the image quality in terms of not only edge enhancement, but also artifacts reductions such as scatter artifacts.

V. CONCLUSION

The proposed SR-CNN demonstrated the capability of substantially augmenting the image quality of under-sampled 3D/4D-CBCT by enhancing the anatomical details and edge information in the images. The improvements of the image quality by SR-CNN potentially allows us to considerably reduce the imaging dose in 3D-CBCT or improve the 4D target localization accuracy based on 4D-CBCT, which is especially critical for lung SBRT patients.