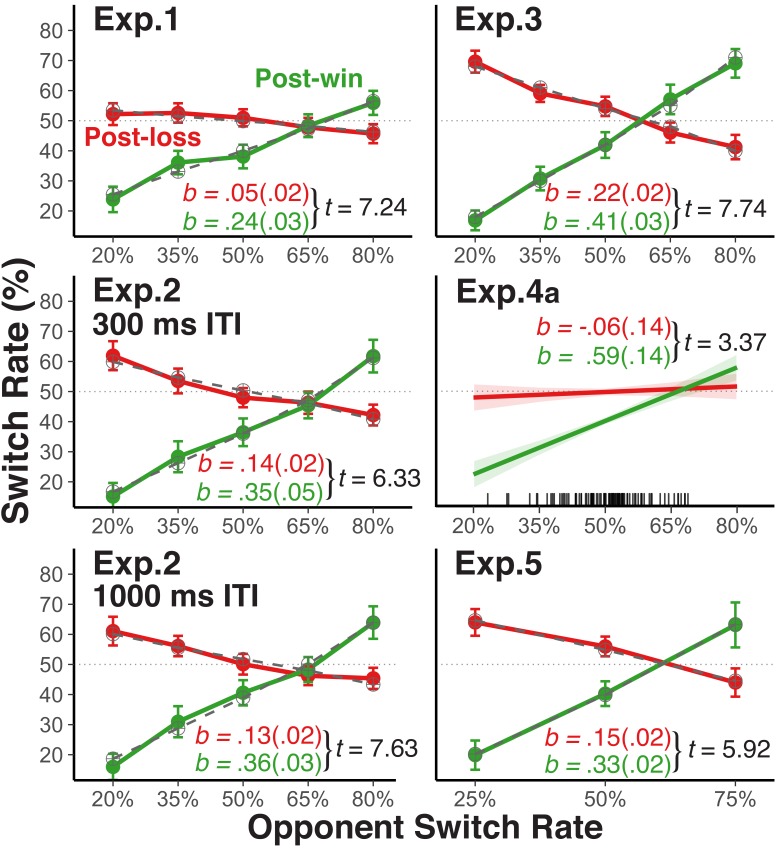
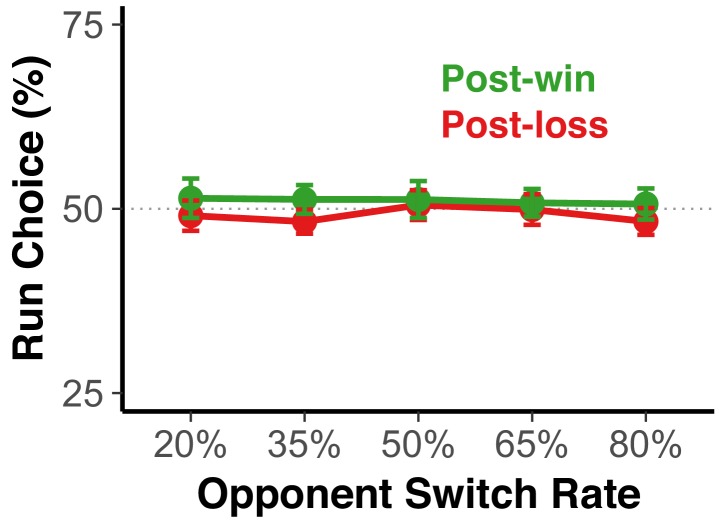
Figure 2. Player's average switch rates as a function of opponents' switch rates.

Average empirical switch rates for post-win and post-loss trials as a function of the simulated opponents’ switch rates for Experiment 1, 2, 3, and five and the average switch rate of each human opponent in Experiment 4a (tick marks on the x-axis indicate individual average switch rates). The dashed lines for Experiment 1, 2, 3, and 5 show the predictions of the theoretical choice model applied to the group average data (see sections Modeling Choice Behavior and Modeling Results). Error bars represent 95% within-subject confidence intervals. For the analyses, we regressed the player’s switch rate on the opponent’s switch rates, the win-loss contrast, and the interaction between these two predictors after reversing the labels of the opponents’ switch rate predictor for post-loss trials (see section Analytic Strategy for Testing Main Prediction). As a test of these interactions, we show the corresponding t-values (SE): the unstandardized slope coefficients (SE; green = post win, red = post loss) were derived from separate analyses for post-win and post-loss trials.

Figure 2—figure supplement 1. Are feedback effects temporary?

Our model assumes that the effect of loss-feedback does not eliminate the model of the opponent, but rather depresses it temporarily. Thus, we should expect that win-loss feedback has a large effect on the next-trial choice, and either no, or only a small effect thereafter. The figure shows for Experiment 1 the switch-rate function from Figure 2, but further conditioned on the trial n-2 win-loss feedback. As apparent, choice behavior is dominated by the effect of trial n-1 feedback. Error bars show 95% within-subject confidence intervals. There was small additional effect of trial n-2 feedback, such that model-based behavior was strengthened following two consecutive wins and stochastic behavior was strengthened following two loss trials (i.e., after two win-trial in a row, the switch-rate function slope becomes more positive, after two loss-trials the function becomes more shallow). Analyzing these data with an ANOVA with the factors trial n-2 and trial n-1 feedback as well as a linear contrast for the opponent switch-rate factor, revealed a strong n-1 feedback x switch-rate interaction, F(1,51)=58.45, p<0.001, eta² = 0.53, and a much weaker, but still reliable n-2 feedback x switch-rate interaction, F(1,51)=15.02, p<0.001, eta² = 0.23, and no three-way interaction, F(1,51)=.25, p=0.91. The results from the remaining experiments were similar to this pattern, and if anything, showed slightly weaker n-2 feedback effects than in Experiment 1. The fact that there was a small, cumulative effect of trial n-2 feedback indicates some degree of adaptation to consistent win or loss feedback contingencies. Yet, the fact that choices are mainly dominated by trial n-1 feedback indicates quick recovery of the last-used model representation following a subsequent win.

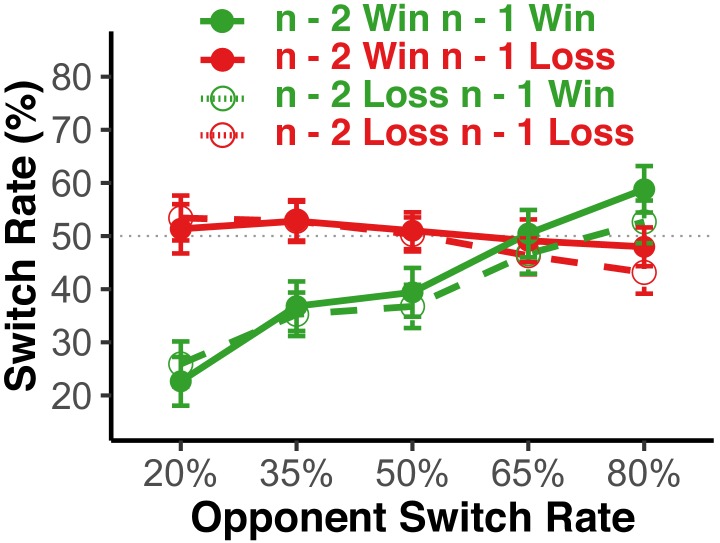
Figure 2—figure supplement 2. Rate of winning as a function of opponent switch rate and n-1 wins/losses.

Model-based behavior can be useful only when the opponent exhibits some degree of regularity. Therefore, we expect that participants show a greater success rate both after win than after loss feedback and when the opponent’s switch rate deviates from chance (p=0.5). This figure shows rate of winning as a function of n-1 wins versus losses and opponents’ switch rate across all experiments with simulated opponents; results for Experiment 2 are collapsed across the two ITI conditions, which showed almost identical patterns. Error bars indicate 95% within-subject confidence intervals. The results confirm expectations: The success rate followed a right-tilted, U-curved function with the most wins for the lowest switch rate, followed by the highest switch rate, and no above-chance success for the mid-range switch rates. Most importantly, this pattern was much more robust for post-win than for post-loss trials. The fact that rate of winning was highest for the opponent with the lowest switch rate, in particular after win trials is consistent with the fact that participants showed a greater tendency for model-based behavior when it required them to engage in low rather than high rates of switching. Within each experiment, the main effect of n-1 wins versus n-1 losses was highly significant (all Fs >= 24.5, p<0.001), as was the interaction between this factor and the quadratic trend for opponent switch rates (all Fs >= 10.77, p=0.003).

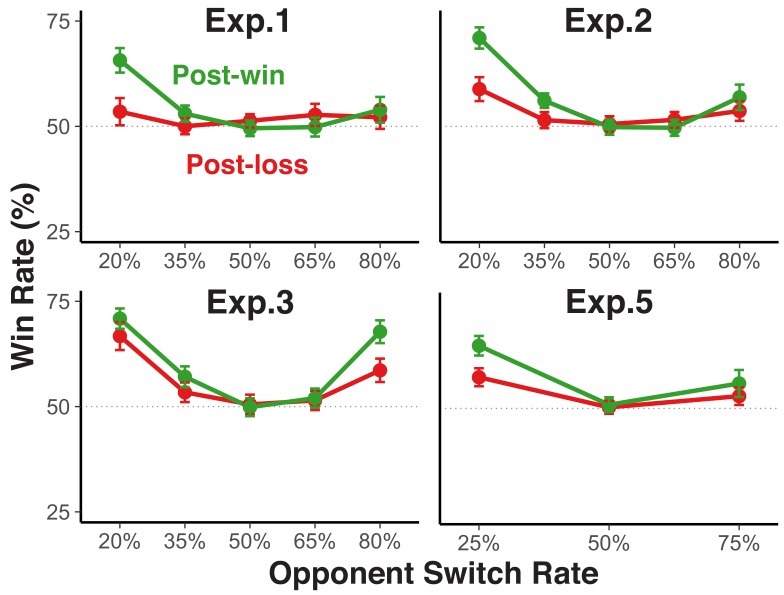
Figure 2—figure supplement 3. Analysis of action choices.

Traditionally, when analyzing choice behavior in experimental games, the focus is on the how players choose between different options. Given that our behavioral signature for model-based and stochastic behavior was based on the rate of switching between action choices, we focused on the rate of switching between options as our primary dependent variable. To ensure that we are not missing important results by only focusing on switch rate, we also examined for all experiments the allocation of choices between the ‘freeze’ and the ‘run’ option (or ‘up’ and ‘down’ for Experiment 3), as well as the degree to which choices were affected by our key independent variables (post-win/post-loss and opponent switch rate). Across all experiments, the choices were fairly evenly distributed (i.e., close to 50% for either option). The independent variables had at best only very small effects that were not consistent across experiments. This figure supplement shows example results from Experiment 1; the pattern for the remaining experiments is very similar. Thus, there are no obvious results in the pattern of action choices that would qualify the conclusions form the switch-rate data.

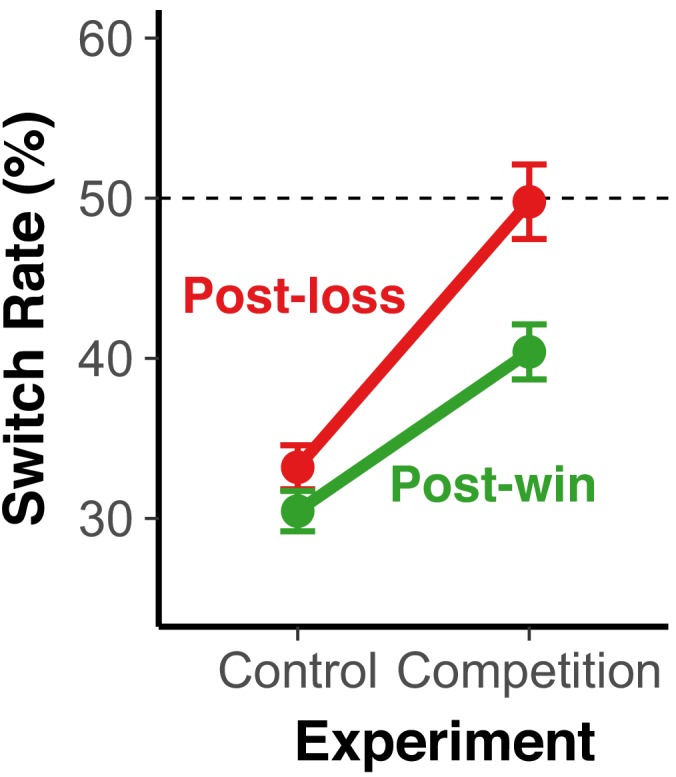
Figure 2—figure supplement 4. Switch rates when competing versus not competing.

The fox-rabbit task is a variant of the voluntary task-switching task, which is a standard paradigm for studying the ability to control selection of action rules in the absence of external prompts (Arrington and Logan, 2004). The most important result in this paradigm is a strong tendency to perseverate the last task/rule (i.e., a switch rate around 30%). In the standard paradigm, subjects are instructed to select tasks as randomly as possible. In contrast, in the fox-rabbit task, the competitive situation in combination with the informative, trial-by-trial feedback should provide an actual incentive to behave unpredictably. Therefore, it is useful to compare performance in the fox-rabbit task to the standard results from the voluntary switching paradigm. The contrast between the competitive situation in Experiment 4a and the non-competitive, but otherwise identical situation in Experiment 4b, allows such a comparison. As apparent, in the control experiment, switch rates were similar to results from the standard voluntary-switching situation and showed no robust feedback effect. In contrast, the competitive situation showed both larger switch rates and a strong win-stay/lose-shift bias (see also Figure 2). The fact that different processes occur in the competitive compared to the non-competitive situation is also apparent form the fact that average RTs in the first are much larger than in the latter (competitive: mean RT = 892 ms, SD = 118; non-competitive: mean RT = 577 ms, SD = 133) at comparable error rates (competitive: mean errors = 5.52%, SD = 1.40; non-competitive: mean errors = 6.80%, SD = 2.21). These results indicate that the competitive situation prompts participants to counter the perseveration bias, albeit at the cost of much longer RTs. This time cost probably reflects the use of the model of the opponent and active processing of the informative feedback--which in turn is likely to introduce the win-stay/lose-shift bias.