Allosteric feedback inhibition of pyridoxine 5′-phosphate oxidase from Escherichia coli

Abstract

In Escherichia coli, the synthesis of pyridoxal 5′-phosphate (PLP), the catalytically active form of vitamin B₆, takes place through the so-called deoxyxylulose 5-phosphate–dependent pathway, whose last step is pyridoxine 5′-phosphate (PNP) oxidation to PLP, catalyzed by the FMN-dependent enzyme PNP oxidase (PNPOx). This enzyme plays a pivotal role in controlling intracellular homeostasis and bioavailability of PLP. PNPOx has been proposed to undergo product inhibition resulting from PLP binding at the active site. PLP has also been reported to bind tightly at a secondary site, apparently without causing PNPOx inhibition. The possible location of this secondary site has been indicated by crystallographic studies as two symmetric surface pockets present on the PNPOx homodimer, but this site has never been verified by other experimental means. Here, we demonstrate, through kinetic measurements, that PLP inhibition is actually of a mixed-type nature and results from binding of this vitamer at an allosteric site. This interpretation was confirmed by the characterization of a mutated PNPOx form, in which substrate binding at the active site is heavily hampered but PLP binding is preserved. Structural and functional connections between the active site and the allosteric site were indicated by equilibrium binding experiments, which revealed different PLP-binding stoichiometries with WT and mutant PNPOx forms. These observations open up new horizons on the mechanisms that regulate E. coli PNPOx, which may have commonalities with the mechanisms regulating human PNPOx, whose crucial role in vitamin B₆ metabolism and epilepsy is well-known.

Introduction

Pyridoxal 5′-phosphate (PLP),² the catalytically active form of vitamin B₆, is involved in many crucial metabolic pathways and plays a fundamental physiological role in all living organisms (1). PLP also performs biological functions other than catalysis, such as those of reactive oxygen species scavenger in plants (2, 3) and Plasmodium falciparum (4), transcriptional regulator in Eubacteria (5), and virulence factor in Helicobacter pylori and Mycobacterium tuberculosis (6, 7). Because of its aldehyde group, PLP is a very reactive molecule that readily combines with thiols and amines. Therefore, it is potentially toxic, and its cellular concentration must be kept at a low level (8). At the same time, large amounts of the cofactor are needed to saturate the many PLP-dependent enzymes and satisfy cell needs. Understanding how these requirements are met (i.e. how PLP homeostasis is regulated and how this vitamer is delivered to apoenzymes that require it as cofactor) is an important target that is far from being reached. PLP is synthesized through two mutually exclusive pathways. The deoxyxylulose 5-phosphate (DXP)-dependent pathway is a multistep process involving seven enzymes and is apparently limited to γ-proteobacteria, such as E. coli (9). In this pathway, the first B₆ vitamer to be produced is pyridoxine 5′-phosphate (PNP), which is then oxidized to PLP by pyridoxine 5′-phosphate oxidase (PNPOx; EC 1.4.3.5). The so-called DXP-independent pathway, which is present in plants, fungi, and most prokaryotes, relies on the action of the PLP synthase complex, which directly produces PLP (10). Organisms that lack both pathways, like mammals, acquire B₆ vitamers from nutrients and protein turnover and interconvert them using a salvage pathway, which includes phosphatases (11, 12), ATP-dependent pyridoxal kinases, and the FMN-dependent PNPOx.

In Escherichia coli, PNPOx (encoded by the pdxH gene) (8) seems to play a pivotal role in PLP homeostasis and delivery to apoenzymes. PNPOx catalyzes the oxidation of PNP or pyridoxamine 5′-phosphate to PLP, reducing molecular oxygen to hydrogen peroxide, using FMN as cofactor. PLP product inhibition of E. coli PNPOx has been reported to take place with a K_I of 8 μm (13) and attributed to PLP binding at the active site; however, data supporting the competitive nature of product inhibition with respect to the PNP substrate have not been presented. This product inhibition is probably an important regulatory mechanism of PLP biosynthesis in E. coli cells, whose free PLP concentration in vivo has been estimated around 120 μm (14). PLP has been proposed to bind with high affinity also at a secondary “tight binding site,” spatially distinct from the active site. This hypothesis is based on observations that when the enzyme is incubated with PLP and then passed through a desalting chromatography column, it retains PLP with a 1:1 stoichiometry ratio with respect to protein subunits (the enzyme is a homodimer (13), in which each subunit binds one FMN molecule (15)) and maintains its catalytic activity almost unaltered (16). In vitro experiments showed that this tightly bound PLP is protected by the solvent and at the same time is readily transferred to apo-PLP–dependent enzymes, such as serine hydroxymethyltransferase (16). Crystallographic studies indicated the possible location of the PLP tight binding site on the surface of the enzyme, at a distance from the active site (17). The actual involvement of this surface pocket, which is symmetrical in PNPOx and therefore present as two sites in the dimeric enzyme, in PLP binding has never been confirmed experimentally. Here, we present data showing that, in net contrast with previous reports, inhibition of E. coli PNPOx by PLP does not result from binding of this vitamer at the active site but from binding at an allosteric site.

Results

Kinetics of pyridoxal 5′-phosphate formation from pyridoxine 5′-phosphate

PNPOx is able to use both PNP and pyridoxamine 5′-phosphate (PMP) as substrates; however, the E. coli enzyme, contrary to its mammalian counterpart that shows similar catalytic efficiency with both substrates, oxidizes PNP with a catalytic efficiency that, at pH 7.6 (which is the internal pH of E. coli cells (18)), is about 50-fold higher (13). This is consistent with the peculiar role played by PNPOx in E. coli, where PNP oxidation is the last step of PLP de novo biosynthesis. In our experiments, we used PNP as substrate, whereas oxygen concentration corresponded to that present in aqueous solutions exposed to air. It may be estimated that, in our reaction conditions, O₂ concentration was roughly 7 mg/liter (0.2 mm). Because K_m for O₂ is around the same value (19), we expect E. coli PNPOx to be half-saturated by O₂ in our reaction conditions. The catalytic activity of PNPOx is usually measured in Tris buffer to avoid accumulation of PLP in the solvent and the consequent product inhibition (20), because PLP forms a Schiff base with Tris and is sequestered from solvent. When we carried out PNPOx activity measurements in a different buffer (50 mm NaHEPES, pH 7.6), in which free PLP is allowed to accumulate in the solvent, we observed complex kinetics that could not be accounted for by simple competitive product inhibition. In HEPES buffer, after mixing substrate and enzyme, a deceleration phase in which the initial velocity of the reaction decreases was observed. This is followed by a slow and constant rate of PLP formation (Fig. 1). This behavior is evident from the first derivative of the kinetic trace, showing that the reaction rate decreases exponentially with a half-time of ∼40 s (Fig. 1, inset). In contrast, in Tris buffer, the reaction rate decreased almost linearly with time. The entire time course of PLP formation observed in Tris buffer could be fitted to a closed form of the time-integrated Michaelis–Menten equation (21), showing that the decrease of reaction rate is accounted for by substrate depletion. The fitting procedure of the kinetics obtained in HEPES buffer failed (data not shown). In this case, at all substrate concentrations, the time course of the reaction may be described as an exponential process followed by a linear phase (Fig. 2A), and data were fitted to an empirical equation describing this behavior (Equation 1), with the intent to estimate the PLP concentration formed in the initial deceleration phase. This analysis showed that the amplitude of the exponential phase increases hyperbolically with substrate, reaching a maximum value of 1.7 ± 0.2 μm (Fig. 2A, inset). This concentration of PLP is definitely higher with respect to the enzyme concentration used in the experiments (0.5 μm). On the other hand, when the enzyme concentration was varied at fixed and saturating substrate concentration (15 μm), the amount of PLP produced in the exponential process increased proportionally (Fig. 2C). The initial velocity of the reactions obtained at different PNP concentrations was measured by linear fitting of the first 25 s of the kinetic traces. Fig. 2B shows that the initial velocity follows a saturation behavior. Because of the low turnover number of the reaction catalyzed by PNPOx (about 0.3 s⁻¹ (15)), in our experiments we were forced to use a relatively high enzyme concentration (0.5 μm) with respect to substrate, which was varied between 1.9 and 100 μm. These conditions are not compatible with classical Michaelis–Menten kinetics, in which the enzyme concentration is much lower than substrate concentration. However, the substrate-binding equilibrium can be assumed to be rapidly established because conversion of the substrate into product is relatively slow. Therefore, the initial rate versus PNP concentration was analyzed with a quadratic equation (Equation 2), which accounts for the decrease of free substrate concentration due to the formation of the enzyme-substrate complex. Kinetic parameters yielded by the analysis were k_cat = 0.28 ± 0.01 s⁻¹ and K_D = 1.6 ± 0.4 μm.

Figure 1.

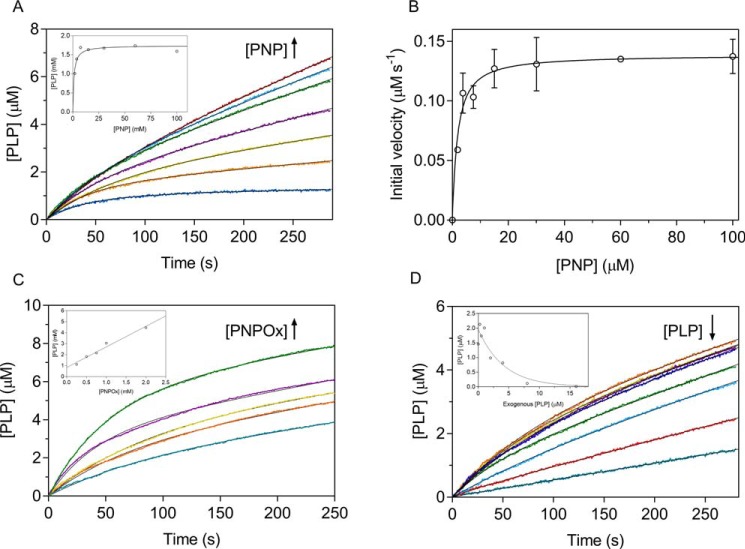
Kinetics of PNP oxidation to PLP in Tris and HEPES buffers. Shown is a comparison of kinetics obtained with 0.5 μm enzyme (protein subunit concentration) and 15 μm PNP, carried out in 50 mm Tris-HCl and 50 mm NaHEPES buffers at pH 7.6. Reactions, carried out at 37 °C, were started by the addition of the enzyme to buffer containing PNP and kept under constant stirring by a magnetic bar, to ensure a rapid mixing. The kinetics trace obtained in Tris buffer was fitted to a closed form of the time-integrated Michaelis–Menten equation (21), whereas the time course of the reaction carried out in HEPES buffer was fitted to Equation 1 (continuous black lines through the experimental traces). The inset shows the first derivative of experimental and theoretical traces. Kinetic traces were exactly the same when the order of addition of reaction components was inverted by adding PNP last.

Figure 2.

Analysis of reactions catalyzed by PNPOx in HEPES buffer. All reactions were carried out in 50 mm NaHEPES buffer, pH 7.6, as explained in the legend to Fig. 1. A, a fixed concentration of enzyme (0.5 μm) was mixed with buffer containing different PNP concentrations (1.88, 3.75, 7.5, 15, 30, 60, and 100 μm). Starting reactions by the addition of substrate as the last component yielded identical kinetics (data not shown). All kinetics were fitted to Equation 1. The inset shows the concentration of PLP formed in the deceleration phase, as determined from fitting, as a function of substrate concentration. The continuous line describes the trend of the experimental points and has no analytical purpose. Values of k_E and k_L parameters found in the fitting are shown in Fig. S1. B, the saturation curve obtained by plotting the initial velocity of the reaction as a function of substrate concentration was analyzed using quadratic Equation 2, obtaining the kinetic parameters reported in Table 1. Error bars, S.E. of the initial velocity values estimated in the fitting procedure. C, increasing enzyme concentration (0.25, 0.5, 0.75, 1, and 2 μm), while keeping PNP concentration fixed (15 μm), proportionally increased the amount of PLP produced in the deceleration phase, as shown in the inset and determined from fitting of kinetics to Equation 1. D, kinetics obtained by the addition of increasing concentrations of exogenous PLP (0, 0.25, 0.5, 1, 2, 4, 8, and 16 μm) to reactions containing 0.5 μm enzyme and 15 μm PNP. Reactions were started by adding PNP as the last component to solutions of enzyme and PLP. However, the order of addition of reactants did not affect kinetics, demonstrating that both PNP and PLP bind rapidly to the enzyme. Fitting to Equation 1 gives the amplitude of the deceleration phase as a function of exogenous PLP concentration (inset). The continuous line has the purpose of describing the trend of experimental points.

These observations indicate that during turnover, a species is produced that slows down the velocity of the reaction and must arise from the accumulation of PLP in solution. To analyze the effect of PLP on reaction kinetics, increasing concentrations of exogenous PLP were included in the reaction mixture, in which enzyme and substrate concentrations were maintained constant. It is clear that PLP has the effect to progressively reduce the overall rate of the reaction and the amplitude of the deceleration phase (Fig. 2D); above 4 μm PLP concentration, the deceleration phase is not apparent. These observations demonstrate that the deceleration observed in HEPES buffer is a consequence of PLP accumulation in the solvent and of its binding to PNPOx. When PMP was used as substrate in HEPES buffer, the rate of PLP formation was extremely slow, making difficult the observation of the deceleration phase, if present (data not shown). With E. coli PNPOx in Tris buffer, other authors observed PNP substrate inhibition (13), which we could not detect even at very high PNP concentration (up to 1 mm; data not shown). Such discrepancy may be attributed to the higher pH (8.5) used in the previous experiments.

Mechanism of PLP product inhibition

The deceleration phase observed in PNP oxidation kinetics results from PLP inhibition, however, is not compatible with a competitive product inhibition. With sheep brain and E. coli PNPOx, inhibition by PLP had been reported to take place with an apparent inhibition constant of 2 μm (22) and 8 μm (13), respectively, and in both cases attributed to PLP binding at the active site. However, data supporting the claimed competitive nature of product inhibition with respect to the PNP substrate had not been presented. To clarify the mechanism of PLP inhibition, a complete inhibition kinetics characterization was carried out in HEPES buffer. Progress time curves obtained at different PNP and PLP concentrations were analyzed to measure the initial velocity of the reaction, and under all conditions, the initial velocities showed a saturation behavior (Fig. 3A). Analysis of saturation curves obtained at increasing PLP concentration with the quadratic Equation 2 shows that PLP affects both apparent k_cat and K_D (Fig. 3B). This behavior is indicative of a mixed-type inhibition (Scheme 1A), in which the inhibitor (PLP in this case) binds to both free and substrate-bound enzymes. Application of the rapid equilibrium hypothesis to Scheme 1A yields the dependences of the apparent k_cat and K_D constants on PLP concentration (see Equations 3–5 under “Experimental Procedures”). Fitting of data in Fig. 3B to these equations allows the estimation of all dissociation and inhibition constants: K_D = 0.90 ± 0.55 μm; K_Dp = 12.85 ± 1.68 μm; K_I = 0.59 ± 0.47 μm; K_Is = 7.13 ± 0.52 μm. A double reciprocal plot of initial velocity data confirms the mixed-type inhibition by PLP (Fig. S2A) and secondary plots of K_m/V_max and 1/V_max as a function of PLP concentration (Fig. S2B) gives inhibition constants consistent with the previous analysis. It should be noticed that 1/V_max and K_m/V_max replots (Fig. S2B) are linear with PLP concentration, indicating that the enzyme activity is completely abolished at infinite PLP concentration, as also showed by the fitting of apparent k_cat as a function of PLP (Fig. 3B).

Figure 3.

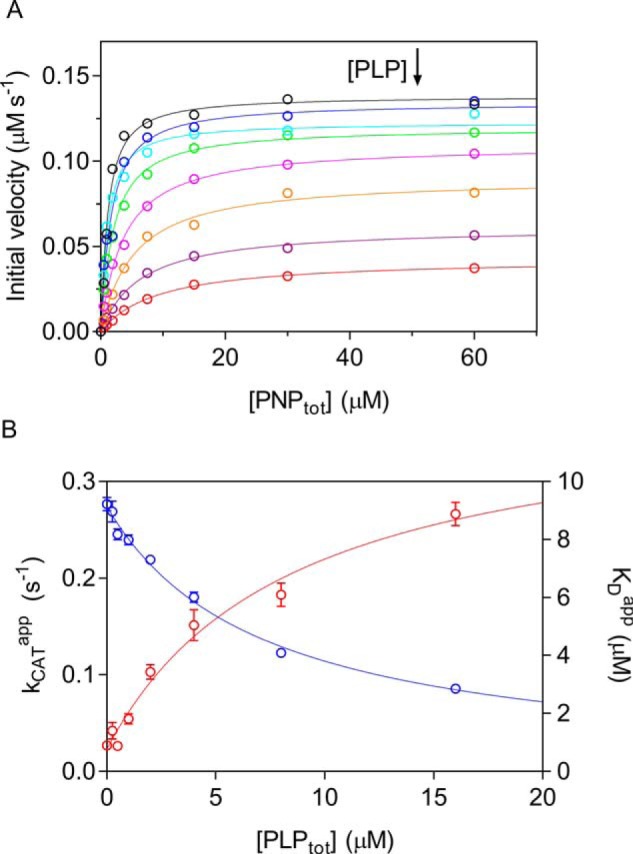
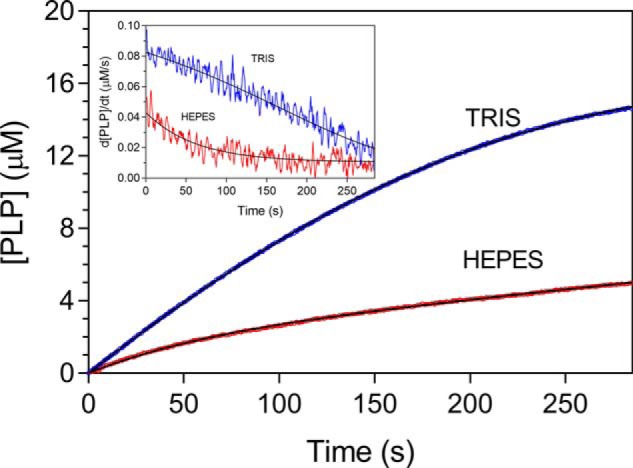
Characterization of PLP inhibition. A, the initial velocity of the reaction was measured with 0.5 μm enzyme (protein subunit concentration), varying PNP concentration while keeping exogenous PLP fixed and at different concentrations (0, 0.25, 0.5, 1, 2, 4, 8, and 16 μm). The obtained saturation curves were fitted to Equation 2, obtaining estimates of apparent k_cat and K_D. B, fitting of apparent k_cat (blue symbols) and K_D (red symbols), using Equations 3–5, as explained under “Experimental procedures,” gave estimates of dissociation and inhibition constants, which are reported in Table 1. Error bars, S.E. of parameter values estimated in the fitting procedure. Concentration of PLP on x axes is the total concentration.

Scheme 1.

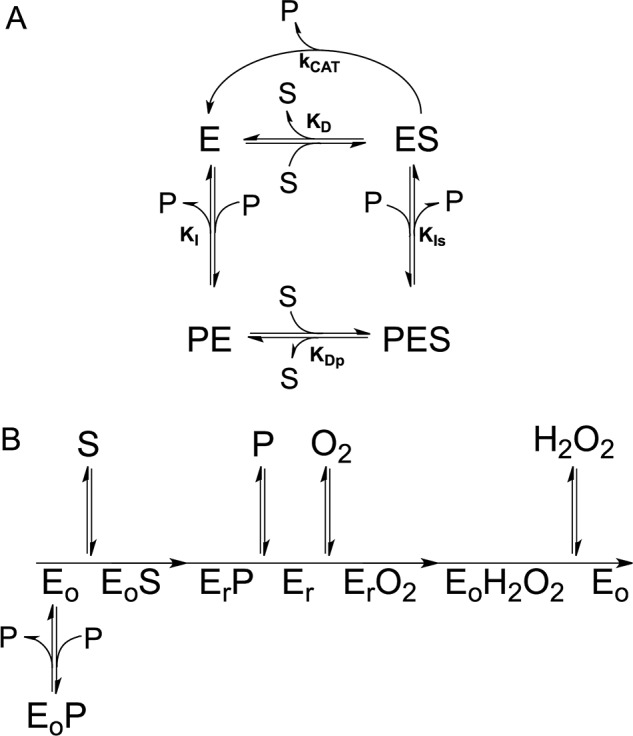
A, steady-state kinetics scheme describing a linear mixed-type inhibition system, in which the enzyme (E) is able to bind both the PNP substrate (S) and the PLP product (P) at the same time. B, ping-pong kinetic mechanism of the reaction catalyzed by PNPOx, in which E_o and E_r are the oxidized form and reduced form of the enzyme, respectively. The PLP product inhibits the enzyme when it binds to the E_o form.

Analysis of PLP-binding equilibrium

PLP binding to PNPOx was characterized by means of spectrofluorimetric measurements, taking advantage of the increase in FMN fluorescence observed upon the addition of PLP to an enzyme solution (Fig. 4). Analysis of data using a quadratic equation (Equation 6) allowed estimate of a dissociation constant of 147 ± 43 nm (Table 1), which is comparable with the K_I for PLP binding to free enzyme determined by inhibition kinetics and is referred to as K_I in Scheme 1A. Titration of more concentrated PNPOx solutions (1, 2, and 4 μm) with PLP, using the same fluorometric method, allowed determination of the stoichiometry of PLP binding to the enzyme, which, in contrast with previous observations (16), was of one PLP molecule per PNPOx dimer (Fig. 4, inset).

Figure 4.

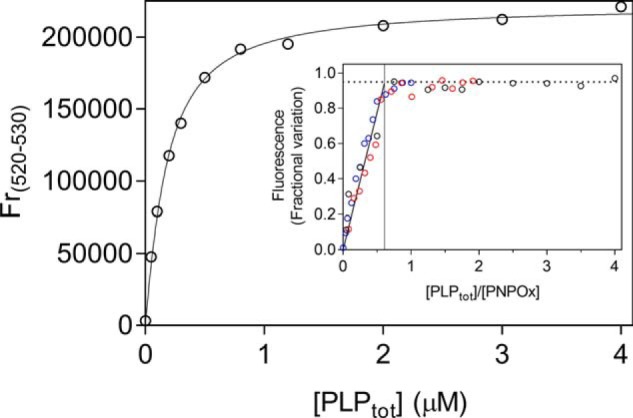
Analysis of PLP-binding equilibrium. Emission spectra (from 470 and 570 nm) of PNPOx in the presence of different PLP concentrations were measured in 50 mm NaHEPES, pH 7.6, upon excitation at 450 nm. The figure shows the PLP-binding curve obtained with 100 nm PNPOx (protein subunit concentration). The average relative fluorescence emission between 520 and 530 nm (F_r(520–530)) as a function of total PLP concentration was analyzed with a quadratic equation describing the binding of a ligand at a single site (Equation 6), using the value of 100 nm protein subunit concentration as a fixed parameter in the fitting procedure. A dissociation constant of 147 ± 43 nm was calculated from the analysis of five independent experiments, such as that shown in the figure. Inset, binding stoichiometry analysis obtained with three different and much higher protein subunit concentrations (1 μm (black symbols), 2 μm (red symbols), and 4 μm (blue symbols)). Fluorescence change, expressed as fractional variation as a function of the [PLP_tot]/[protein] ratio, is linear as shown by the thick continuous line, up to the stoichiometry point corresponding to the crossing with the horizontal dotted line. The vertical thin line through the stoichiometry point indicates that about one PLP molecule binds per enzyme dimer.

Table 1.

Parameters obtained from kinetic and equilibrium measurements on PNPOx forms

Names of parameters listed in the table refer to Scheme 1A.

Parameter	WT	Apo-WT	Quadruple mutant
Kinetics of PNP oxidation
kcat (s−1)a	0.3 (15)		5.3 × 10−4 ± 0.7 × 10−4
KD (μm)a	2 (15)		238 ± 77
kcat (s−1)b	0.28 ± 0.01
KD (μm)b	1.6 ± 0.4
Inhibition kinetics
kcat (s−1)c	0.27 ± 0.01
KD (μm)c	0.90 ± 0.55
KDp (μm)c	12.85 ± 1.68
KI (μm)c	0.59 ± 0.7
KIs (μm)c	7.13 ± 0.52
PLP binding
kon (μm−1 s−1)d	11.35 ± 1.27
koff (s−1)d	3.24 ± 2.24
KI (μm)d	0.28 ± 0.19
KI (μm)e	0.15 ± 0.04	0.28 ± 0.01	0.45 ± 0.02

^a Determined in Tris buffer.

^b Determined in HEPES buffer from fitting of initial velocity.

^c Determined from PLP inhibition kinetics.

^d Determined from rapid kinetics measurements of PLP binding.

^e Determined from equilibrium measurements.

Stopped-flow kinetics

The PNPOx-PLP binding reaction was also studied by stopped-flow spectroscopy to probe the kinetic on- and off-rate constants (Fig. 5) and took advantage of the same FMN fluorescence changes upon PLP binding used in the equilibrium experiments. In these experiments, 20 μm PNPOx was mixed in the stopped-flow apparatus with increasing PLP concentrations (from 2 to 37 μm before mixing) at 25 °C. All kinetic traces were biphasic, comprising a fast phase with increasing fluorescence and a slow phase with decreasing fluorescence intensity (Fig. 5A). The observed time courses were fitted to Equation 7 and are consistent with a two-step mechanism shown in Scheme 2, in which a second-order reaction determining an increase of fluorescence is followed by a first-order process converting the enzyme-PLP complex to a species E-PLP* with decreased fluorescence. Consistently, the fast phase depended on PLP concentration, whereas the slow phase was independent of PLP concentration (Fig. 5B). Fitting of data to Equation 8 yielded the following results: k_on = 11.35 ± 1.27 μm⁻¹ s⁻¹ and k_off = 3.24 ± 2.24 s⁻¹ and thus a dissociation constant (k_off/k_on) of 0.28 ± 0.19 μm (which in Scheme 1A is referred to as K_I and represents binding of PLP to free enzyme), in excellent agreement with the equilibrium experiments described above and with K_I determined in inhibition kinetics. Because the slow phase was clearly independent of PLP concentration, with an average value of k_slow = 0.73 ± 0.12 s⁻¹, we assign this phase to a process taking place within the PNPOx-PLP complex. Given that the absorption spectrum of the PNPOx-PLP complex excludes the formation of a Schiff base (based on the absence of the characteristic 420 nm peak (16)), we propose the slow phase to consist of a rearrangement of PLP within the PNPOx binding pocket or to a protein conformational change that affects the FMN microenvironment. The use of Equation 8 is also supported by numerical integration simulations of Scheme 2, which predicted correct k_on and k_off values to within 1–5% (data not shown).

Figure 5.

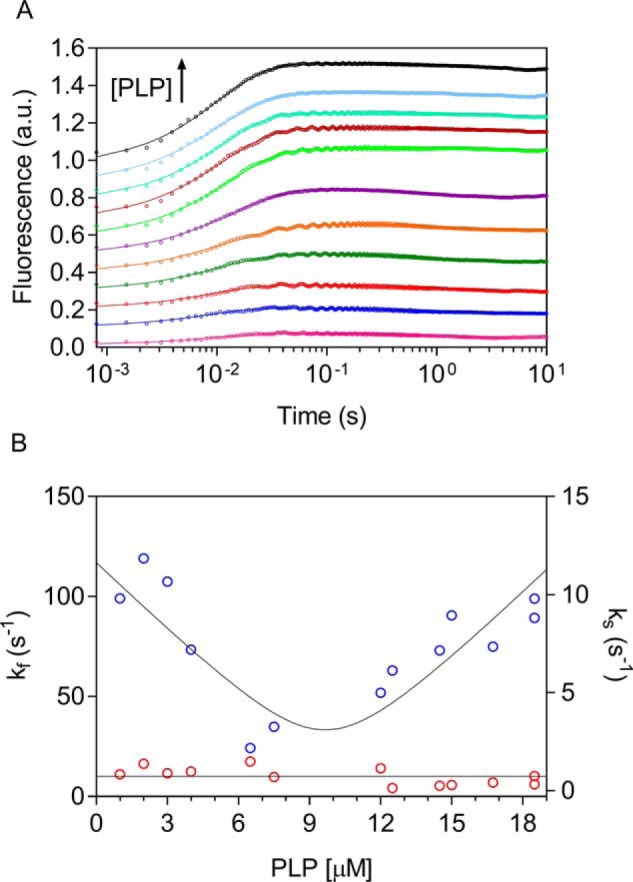
PLP binding as measured by stopped-flow spectroscopy. 20 μm PNPOx (protein subunit concentration) was mixed 1:1 in the stopped-flow apparatus with PLP (2, 4, 6, 8, 13, 15, 24, 25, 29, 30, 33, and 37 μm) in NaHEPES buffer at 25 °C. A, for a better view, the time courses of the reactions were offset by 0.1 fluorescence units on the y axes by adding an increasing value and are shown on a log(time) scale. Traces were fitted to Equation 7 (solid lines). B, dependence of k_fast (k_f; blue symbols) and k_slow (k_s; red symbols) on PLP concentration after mixing; k_fast was fitted to Equation 8, and k_slow was fitted to a line with slope = 0 (solid lines).

Scheme 2.

Kinetic mechanism of PLP binding to PNPOx. See “Results” for a description of this mechanism.

Location of the PLP-binding site

The question arises whether PLP binding observed by fluorometric measurements takes place at the active site or at a secondary, allosteric site. We addressed this problem by using forms of the enzyme whose capability to bind the PNP substrate at the active site is heavily impaired: the apoenzyme and an active site mutant. Both PNP and PLP bind at the active site of PNPOx, making stacking interactions with the FMN cofactor (17). Elimination of FMN is expected to affect PLP binding at the active site. The intrinsic fluorescence of apo-PNPOx, deprived of its FMN cofactor, was measured at increasing PLP concentrations. A decrease of fluorescence was observed, which allowed determination of a dissociation constant (corresponding to K_I) of 279 ± 9 nm (Fig. 6), which is not very different from that obtained with the holo-form of the enzyme. We also introduced amino acid mutations in PNPOx with the intent to impair PLP binding at the active site. A quadruple PNPOx mutant (K72I/Y129F/R133L/H199A) was produced, in which four crucial amino acid residues involved in the electrostatic binding of the substrate phosphate (23) were replaced by hydrophobic residues (Fig. 7). This mutant enzyme has a very small residual activity that allowed determination of kinetic parameters in Tris buffer: k_cat = 5.3 × 10⁻⁴ ± 0.7 × 10⁻⁴ s⁻¹ and K_m = 238 ± 77 μm, which are 560-fold lower and 120-fold higher, respectively, than those of WT PNPOx (23) (Table 1). This mutant enzyme with very reduced capacity to use PNP as substrate is still able to bind PLP, as demonstrated by fluorometric measurements (Fig. 6), with a dissociation constant (446 ± 23 nm) that is comparable with that of the WT enzyme. Differently from the WT enzyme, titration of concentrated solutions of the mutant enzyme with PLP gave a binding stoichiometry of two PLP molecules per enzyme dimer (Fig. 6, inset).

Figure 6.

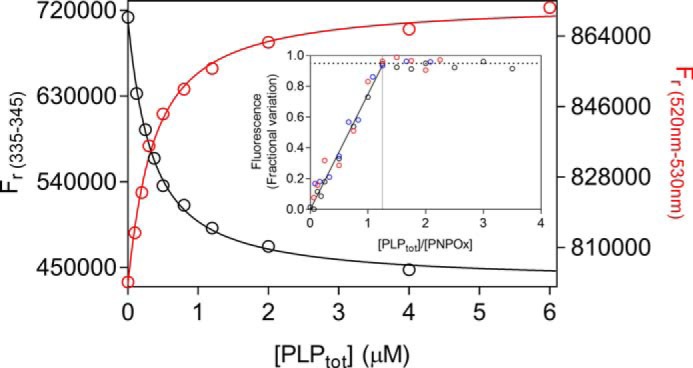
PLP binding to enzyme forms with altered active site structure. Fluorometric analysis of PLP binding to apo-PNPOx (100 nm, protein subunit concentration) was carried out exciting at 280 nm. The average fluorescence emission between 335 and 345 nm was plotted against total PLP concentration (black symbols). PLP binding to the holo-form of the quadruple mutant (red symbols) was analyzed as described previously for WT holo-form PNPOx. Both sets of data were fitted using the quadratic Equation 6, obtaining K_D values reported in Table 1. Inset, binding stoichiometry analysis obtained with three different and much higher concentrations of the quadruple PNPOx mutant, as explained in Fig. 4 for the WT enzyme. Protein subunit concentrations were 4 μm (black symbols), 8 μm (red symbols), and 12 μm (blue symbols).

Figure 7.

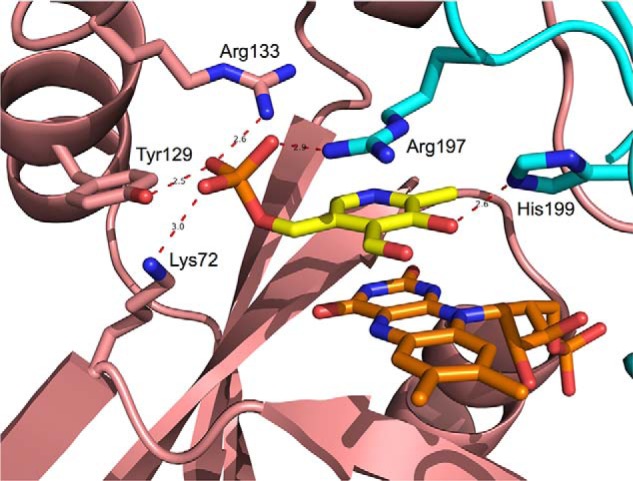
Enlarged view of PNPOx active site structure. Cartoon backbone representation of the E. coli PNPOx dimer (Protein Data Bank code 1G79) with PLP bound at the active site. The two subunits are shown in cyan and salmon, respectively. Active site residues involved in binding of PLP are shown as sticks and labeled. Interatomic distances indicated by red dashes are expressed in Å. It can be assumed that the PNP substrate binds by establishing the same interactions with active-site amino acid residues (23).

Retention of PLP by PNPOx and activity of the PLP-PNPOx complex

It is known by previous experiments that E. coli PNPOx binds PLP so tightly that, when incubated with it and then passed through a desalting column, it retains PLP with a 1:1 ratio (100% with respect to protein subunits), and maintains 85% catalytic activity (16). We have repeated this experiment with both WT and mutant PNPOx forms. Both enzyme forms at 100 μm concentration were incubated with an equimolar amount of PLP and then passed through a size-exclusion chromatography column (Superdex 200 10/300 GL column) using an FPLC system, obtaining a good separation between unbound PLP and protein. The experiment was carried out in triplicate with each enzyme form. The stoichiometric binding of PLP to the proteins was calculated as 66 ± 26% (with respect to protein subunits) with WT PNPOx and 37 ± 9% with the quadruple mutant. We also measured the kinetics of PLP formation in HEPES buffer using the WT PNPOx-PLP complex obtained from chromatography and a control enzyme sample that was not incubated with PLP. When using a final concentration of 0.5 μm enzyme in the assay, we could not observe any difference in the obtained kinetics. However, with 8 μm enzyme, kinetic profiles were very different: the PNPOx-PLP complex gave slower kinetics that lacked the first deceleration phase (Fig. 8).

Figure 8.

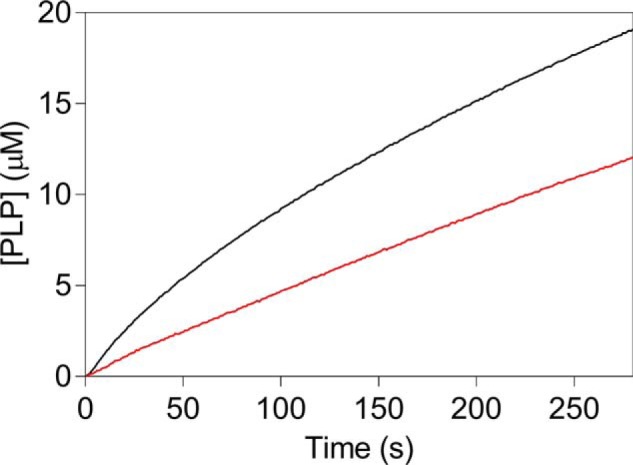
Kinetics of PNP oxidation to PLP in HEPES buffer catalyzed by WT PNPOx with tightly bound PLP. Reactions were carried out as explained in the legend to Fig. 1 and started by diluting enzyme samples, either the PNPOx-PLP complex obtained after incubation with PLP and size-exclusion chromatography (red trace) or an untreated control PNPOx sample (black trace) in 50 mm NaHEPES buffer, pH 7.6, containing PNP, obtaining 8 μm enzyme and 240 μm substrate final concentrations.

Discussion

Previous investigations on PNPOx from E. coli (13) and rabbit liver (24, 25) had revealed PLP inhibition, proposing that PLP binds at the active site and competes with substrates. These observations relied on discontinuous enzymatic assays and on a manual mixing of enzyme and substrate. In our case, a more sensitive continuous spectrophotometric assay and a relatively rapid mixing allowed detection of a deceleration phase in the kinetics of PLP formation (Fig. 1) and showed that PLP inhibition has a mixed-type nature (Fig. 3). The deceleration phase is quite prolonged over time and cannot possibly result from an intrinsic feature of the reaction mechanism, such as that typical of the “ping-pong” mechanism, also because the amount of product produced in this phase is 3-fold higher than the enzyme concentration. Nor can it result from the presence of an impurity in the PNP substrate endowed with higher reactivity, because the amount of PLP produced in the deceleration phase reaches a maximum value as substrate concentration is increased (Fig. 2A, inset). Moreover, this amount of PLP is proportional to the enzyme concentration and tends to a minimum value as the enzyme concentration approaches zero (Fig. 2C). The deceleration phase is directly linked to PLP concentration in the solvent. Indeed, the initial velocity of the reaction decreases, and therefore the deceleration phase becomes less evident until it disappears, as the exogenous PLP concentration is increased (Fig. 2D). Furthermore, the deceleration phase is absent in Tris buffer, where PLP is sequestered from the solvent as it forms from PNP (Fig. 1). All of these observations indicate that the initial deceleration phase results from PLP accumulation in the solvent and from the consequent onset of PLP inhibition. The following interpretation of data are possible. Immediately after mixing enzyme and PNP, when there is not yet PLP in the solvent, the maximum reaction rate is observed. As PLP is formed and accumulates in the solvent, it progressively binds to the enzyme at an allosteric site, determining a decrease of reaction rate, until this binding equilibrium reaches saturation. At this point, the enzyme is only partially inhibited and catalyzes PNP oxidation at a rate that is neatly lower than the initial rate. The concentration of PLP formed in the deceleration phase is determined by the affinity of the allosteric PLP binding site; it corresponds to the concentration that is sufficient to saturate the allosteric site and depends on both substrate (Fig. 2A, inset) and enzyme (Fig. 2C, inset) concentrations. Our experiments on the catalytic activity of the PNPOx-PLP complex, obtained after incubation with PLP and size-exclusion chromatography, confirm this interpretation and are not in contrast to the results obtained by other authors (16). These authors carried out activity assays in Tris buffer and obtained 85 ± 2% activity for the PNPOx-PLP complex, as compared with an untreated PNPOx sample. We know that Tris buffer certainly promotes dissociation of PLP from the enzyme-PLP complex. Moreover, activity assays were carried out with a low concentration of enzyme, diluting the concentrated PNPOx-PLP complex and therefore promoting PLP dissociation. We know from our rapid kinetics studies that PLP dissociation is rapid enough to reach equilibrium in a few seconds (k_off = 3.24 s⁻¹ and k_on = 11.35 μm⁻¹ s⁻¹; Table 1). In fact, when we measured the kinetics of PNP oxidation to PLP in HEPES by diluting the PNPOx-PLP complex to 0.5 μm, we could not observe any difference with respect to a control PNPOx sample. However, with 8 μm PNPOx-PLP complex, a neat difference was observed, consisting of the lack of the decelerating phase and a reduced activity (Fig. 8), similar to what was observed when exogenous PLP was included in the reaction mixtures (Fig. 2D). It is evident that, with concentrated PNPOx-PLP complex, dissociation of PLP takes place to a lesser extent.

PLP inhibition kinetics have the properties of a mixed-type system (Fig. 3 and Fig. S2). Work from several years ago (19) showed that PNPOx purified from rabbit liver followed a substituted-enzyme (ping-pong) mechanism when acting on PNP as substrate. According to this mechanism, PNP is converted into PLP in the first half-reaction, leaving the enzyme in the reduced form. In the second half-reaction, molecular oxygen binds to this form of the enzyme and is reduced to H₂O₂ (Scheme 1B). In the ping-pong mechanism, PLP is expected to give a mixed-type inhibition when PNP is the variable substrate and oxygen is not saturating (26), which results from binding of PLP at the active site of two different forms of the enzyme with different affinity. In our case, because K_m for PNP increases as PLP is increased, the oxidized form (E_o in Scheme 1B) should bind PLP with higher affinity than the reduced form (E_r). However, if this were the case for E. coli PNPOx, saturation of the higher-affinity site would result in complete inactivation, because all enzyme would be in the E_o·PLP form. This hypothesis must be ruled out, because in our experiments, when PLP (either produced from PNP or exogenously added to the reaction mixture) was present at a concentration sufficient to saturate the higher-affinity site, we observed only a partial inactivation. Besides, it would be unusual if PLP had a higher affinity for E_o than for E_r. On the other hand, binding of PLP only to E_r would give an inhibition in which both K_m and k_cat are decreased as PLP is increased (as shown in simulations based on a ping-pong mechanism that we have carried out; data not shown). A mixed-type inhibition based on the ping-pong mechanism implies that PLP inhibits PNPOx by binding at the active site. However, alteration of the active site (such as the elimination of FMN in the apoenzyme and the mutations in the quadruple PNPOx mutant) does not drastically affect PLP binding, as shown by fluorometric measurements (Table 1). Moreover, mixed-type inhibition resulting from a ping-pong mechanism would not yield biphasic kinetics as we observed, but a progressive decrease of reaction velocity as substrate is consumed in the course of the reaction, as in simple steady-state kinetics (this was also verified by simulations). A mixed-type product inhibition may also result from a compulsory-order sequential mechanism (26). However, the same objections invoked for the ping-pong mechanism also apply to this mechanism. Therefore, an alternative interpretation must be adopted for E. coli PNPOx that prescinds from the kinetic mechanism, in which PLP binds at an allosteric site, distinct from the active site. This possibility is depicted in Scheme 1A, which is a steady-state kinetics scheme that applies to both ping-pong and sequential mechanisms. This model is that of a classic linear mixed-type inhibition, in which binding equilibria of substrate and inhibitor to the enzyme are rapidly established and conversion of the substrate into product is relatively slow. Binding of PNP at the active site and binding of PLP at the allosteric site influence each other, increasing their respective dissociation constants (27). Accordingly, two inhibition constants are measured, resulting from binding of PLP with higher affinity to the free enzyme (K_I) and with lower affinity to the enzyme-substrate complex (K_Is). Simulations based on Scheme 1A (and on a ping-pong mechanism in which PLP binds to an allosteric site, as well as to E_r) gave very similar results to those we obtained experimentally, in which biphasic kinetics and a mixed-type inhibition are observed. Noticeably, K_I determined from our inhibition kinetics is similar to the dissociation constant determined in the fluorometric and rapid kinetics experiments, which used the free enzyme form (Table 1). Analogously, different kinetic parameters are obtained from inhibition kinetics: K_D, which is relative to substrate binding to the free enzyme, and K_Dp, due to substrate binding to the enzyme-PLP complex (Fig. 3 and Table 1). A comparable value of K_D was obtained from fitting of the initial velocity in HEPES buffer (Fig. 2B and Table 1). The fact that 1/V_max and K_m/V_max replots (Fig. S2B) are linear with PLP concentration and the enzyme activity is completely abolished at infinite PLP concentration, as shown by the fitting of apparent k_cat as a function of PLP (Fig. 3B), indicates that the enzyme-PNP-PLP complex (PES in Scheme 1A) is completely inactive (otherwise replots would be hyperbolic) and that PLP does not compete with the PNP substrate for binding at the active site (otherwise, replots would be parabolic) (27). As shown by the crystal structure obtained in the presence of PLP (17), this vitamer is able to bind at the active site. Evidently, binding at the active site takes place with much lower affinity with respect to binding at the allosteric site, so that it is not detected in our experiments.

The presence of an allosteric PLP binding site on E. coli PNPOx is also demonstrated by fluorometric measurements on the quadruple mutant. Although in this mutant substrate binding at the active site is heavily impaired, the enzyme is still able to bind PLP with a dissociation constant (446 ± 23 nm) that is in the range of that measured with the WT enzyme (Table 1). However, the stoichiometry of PLP binding is affected by the active site mutations. With the WT enzyme, the measured stoichiometry of one PLP molecule per protein dimer (Fig. 4, inset) is against the presence of two symmetric PLP binding sites, such as the secondary PLP binding sites indicated by the crystallographic data (17). This suggests that the allosteric PLP binding site may be located along one of the two symmetry axes of the dimer. Alternatively, if two symmetric PLP binding sites are present on the PNPOx dimer, binding of PLP at one site should cause a conformational change that prevents binding at the second site. This second hypothesis may be supported by the different PLP-binding stoichiometry obtained with the quadruple mutant, which is of two PLP molecules per enzyme of dimer (Fig. 6, inset). The structural and functional connection between the active site and the allosteric site is at the basis of the allosteric inhibition acted by PLP. This is evident in the revealed mixed-type inhibition mechanism, in which substrate binding and PLP binding affect each other. Therefore, it is possible that a substantial alteration of the active site, such as that present in the quadruple mutant, may have uncoupled the allosteric connections.

The presence of an allosteric PLP-binding site is also confirmed by the capability of the quadruple mutant to retain PLP upon size-exclusion chromatography, although in these experiments, the stoichiometry of PLP binding to WT (66 ± 26% protein-bound PLP, with respect to protein subunits) and mutant (37 ± 9%) enzymes is somewhat surprising if compared with stoichiometry obtained from equilibrium binding experiments. Yang et al. (16) reported 100% of PLP binding to WT PNPOx in analogous experiments; however, these authors used a short-gravity chromatography BioGel P6-DG desalting column. In our more resolving conditions, dissociation of PLP from the PNPOx-PLP complex is surely favored. This could explain the low PLP content of the quadruple mutant protein-PLP complex, also considering that binding of PLP at its active site is nearly abolished. On the other hand, PLP binding at the active site may account for the larger than expected PLP content in the WT PNPOx-PLP complex.

E. coli PNPOx is a catalytically sluggish but relatively abundant enzyme (13). These features, together with the allosteric feedback inhibition demonstrated by our studies, underlie the important regulatory role of this enzyme, whose function is to produce PLP and at the same time keep its concentration in the free form at a low level, while making it available in large and nontoxic amounts in a protein-bound form. The dual nature of PNPOx as catalyst and PLP-carrier protein is shared by pyridoxal kinase (encoded by pdxK) that is also inhibited by PLP and binds this cofactor tightly but at the same time is capable of transferring it to apo-serine hydroxymethyltransferase, a model PLP-dependent enzyme whose mechanism of addition of PLP has been studied in detail (28–30). The E. coli COG0325 protein (encoded by yggS) (31), which apparently is not endowed with any catalytic activity, probably only plays the role of PLP carrier protein, although its capability of transferring PLP to apoenzymes has not yet been demonstrated. Surely, its human homologue, named PROSC, has a crucial role in PLP homeostasis, because its mutation causes epilepsy (32). Because also human PNPOx, which is structurally very similar to its E. coli homologue, is inhibited by PLP (33), our observations on the E. coli PNPOx might also apply to this enzyme and be of fundamental importance in human B6 metabolism and in diseases caused by PNPOx mutations (34). The actual location of the allosteric PLP-binding site involved in the inhibition detected in our experiments awaits determination. The possible connection to the PLP secondary binding site indicated by crystallographic data (17) is presently under study by our research group.

Experimental procedures

Materials

Ingredients for bacterial growth and all reagents used for protein purification were from Sigma-Aldrich, except for DEAE-Sepharose and phenyl-Sepharose, which were purchased from GE Healthcare (Milwaukee, WI). Pyridoxine 5′-phosphate was obtained from pyridoxal 5-phosphate (98% pure; Sigma-Aldrich) according to the method of Kazarinoff and McCormick (35).

Protein expression and purification

E. coli WT and mutant PNPOx forms were expressed using a pET22 construct containing the pdxH gene (15), transformed into E. coli MDS00 strain cells lacking pdxH (36), and purified as described previously (15). Apo-PNPOx was obtained by chromatographic separation (37). The protein subunit concentration of apo-PNPOx and holo-PNPOx was calculated according to the method developed by di Salvo et al. (15), which also takes into account the contribution of FMN to the absorbance at 278 nm.

Site-directed mutagenesis

Mutation of the pdxH coding region to obtain the quadruple K72I/Y129F/R133L/H199A PNPOx mutant was carried out using the above-mentioned pET22 construct as template and a standard protocol described in the QuikChange kit from Stratagene (La Jolla, CA). For each mutation, two complementary oligonucleotide primers, synthesized by Metabion International AG (Steinkirchen, Germany), were used. The following are the sequences of the forward primers, in which the mutated bases are underlined: K72I, 5′-GCA TCG TTT TAC TCA TAC ATT ACG ACG AA-3′; Y129F, 5′-CTC GAA GTG ATG AAA TTT TTT CAT AGC CGC CC-3′; R133L, 5′-GAA ATA TTT TCA TAG CCT CCC GCG TGA TAG C-3′; H199A, 5′-GAG CAT CGC CTG GCT GAC CGC TTT TTG TAC-3′. E. coli DH5α cells were used to amplify the mutated plasmids. All mutations were confirmed by sequence analysis of both DNA strands, and the only differences with respect to WT were those intended. Enzyme expression was performed using the E. coli MDS00 strain (36).

Kinetic studies

Kinetic measurements were performed using a Hewlett-Packard 8453 diode-array spectrophotometer (Agilent Technologies, Santa Clara, CA), using a 1-cm path length cuvette, at 37 °C in 50 mm NaHEPES buffer at pH 7.6. Product formation was followed at 388 nm, where PLP absorbs maximally with a molar absorbance coefficient of 5330 m⁻¹ cm⁻¹, as calculated from standard PLP solutions, whose concentration was determined in 0.1 m NaOH (38, 39). Activity assays were also carried out in 50 mm Tris-HCl, pH 7.6. In this case, an extinction coefficient of 4253 m⁻¹ cm⁻¹ at 414 nm was calculated for PLP.

Determination of the dissociation constant of the PLP-binding equilibrium

Analyses took advantage of FMN fluorescence increase observed upon binding of PLP to PNPOx. Dissociation constants were calculated from saturation curves obtained measuring the protein fluorescence emission intensity as a function of increasing ligand concentration. Fluorescence emission measurements were carried out at 25 °C, in 50 mm NaHEPES buffer at pH 7.6 with a FluoroMax-3 Jobin Yvon Horiba spectrofluorometer, using a 1-cm path length quartz cuvette. All analyzed PNPOx forms were used at a final subunit concentration of 0.1 μm. Fluorescence emission spectra were recorded from 470 to 570 nm upon excitation at 450 nm. Excitation and emission slits were set at 3 and 5 nm, respectively. Emission fluorescence values between 520 and 530 nm were averaged and analyzed using a quadratic equation (Equation 6). Titration experiments carried out to determine the stoichiometry of PLP binding to PNPOx were performed using the same method with excitation and emission slits set at 1 and 3 nm, respectively. PLP binding to apo-PNPOx was analyzed owing to the protein intrinsic fluorescence emission quenching observed upon binding under excitation at 280 nm. Emission spectra were recorded from 300 to 450 nm, with excitation and emission slits set at 3 and 5 nm, respectively. Fluorescence emission values between 335 and 345 nm were averaged and analyzed according to a modified version of Equation 6.

Stopped-flow experiments

The PLP dissociation constant was also determined by stopped-flow spectroscopy. Kinetic binding experiments were carried out on a thermostated SX-17 stopped-flow instrument (Applied Photophysics, Leatherhead, UK) with high fluorescence sensitivity and low inner filtering, in 50 mm NaHEPES buffer at pH 7.6, at 25 °C. Protein-bound FMN was excited at 445 nm, and total fluorescence emission was collected by using a 510-nm cut-off glass filter. In these experiments, PNPOx was mixed in the stopped-flow apparatus with solutions of PLP of increasing concentration from 2 to 37 μm before mixing. Because fluorescence changes were very small, the enzyme concentration was increased to 20 μm (before mixing), and several traces (10–15 traces) at each PLP concentration were acquired and averaged to increase the signal-to-noise ratio. The time courses were acquired on a logarithmic time scale to measure both the fast and slow phases.

Retention of PLP by PNPOx and measurement of the activity of the PNPOx-PLP complex

Either WT or quadruple mutant PNPOx (100 μm) was incubated with an equimolar amount of PLP at 30 °C for 30 min. The mixtures were loaded onto a size-exclusion chromatography column (Superdex 200 10/300 GL column) and eluted using an FPLC system, AKTA Prime (GE Healthcare). Fractions (0.8 ml) were collected, and spectra were recorded. The elution profile obtained by plotting absorbance at 390 nm, characteristic of PLP, demonstrated that PLP eluted after the protein and separated well from it. The number of PLP molecules bound per protein subunit was calculated as in di Salvo et al. (40), by releasing protein-bound PLP with 0.5 m KOH, neutralizing with HClO₄, and using E. coli apoSHMT as a PLP trap. The amount of PLP present in the PNPOx samples was calculated from the activity of reconstituted holo-SHMT by a comparison with a standard curve constructed by adding known amounts of PLP to apoSHMT.

Data analysis

Data were analyzed using the software Prism (GraphPad Software Inc., San Diego, CA) or Matlab (Mathworks). Kinetics of PLP formation from PNP obtained in HEPES buffer were analyzed with an empirical equation describing an exponential process followed by a linear phase.

$$y={\alpha }_E\left(1-e^{-k_{E}t}\right)+k_{L}t$$ (Eq. 1)

Steady-state kinetic parameters (k_cat and K_D) in HEPES buffer were determined by nonlinear least-squares fitting of initial velocity data shown in Figs. 2B and 3A to the quadratic equation, Equation 2, in which v_i is the initial velocity of the reaction, k_cat·[E₀] corresponds to V_max of the reaction, [PNP₀] is the total substrate concentration, [E₀] is the total enzyme concentration, and K_D is the dissociation constant of the substrate-binding equilibrium E + PNP ⇋ E·PNP, assuming a rapid establishment of the equilibrium, is equivalent to K_m.

$$v_i=k_{\text{cat}}\left[E_0\right]\frac{\begin{array}{c}\left[PN{P}_0\right]+\left[E_0\right]+K_D\\ -\sqrt{{\left(\left[PN{P}_0\right]+\left[E_0\right]+K_D\right)}^2-4\left[PN{P}_0\right]\left[E_0\right]}\end{array}}{2\left[E_0\right]}$$ (Eq. 2)

Kinetic parameters of the quadruple mutant in Tris buffer were obtained by fitting initial velocity data as a function of substrate concentration using the Michaelis–Menten equation.

Apparent k_cat and apparent K_D values obtained from PLP inhibition studies were fitted to Equations 3 and 4, respectively, in which K_Is, K_D, K_Dp, and k_cat are those indicated in Scheme 1A. Because Scheme 1A comprises a thermodynamic cycle, K_I was determined through Equation 5, which is based on the principle of detailed balance.

$$k_{\text{cat}}^{\text{app}}=\frac{K_{Is}}{K_{Is}+\left[PLP\right]}{K}_{\text{cat}}$$ (Eq. 3)

$$K_D^{\text{app}}=\frac{K_D{K}_{Is}+K_{Dp}\left[PLP\right]}{K_{Is}+\left[PLP\right]}$$ (Eq. 4)

$$K_I=\frac{K_D{K}_{Is}}{K_{Dp}}$$ (Eq. 5)

Fluorescence data obtained in PLP-binding equilibrium experiments were analyzed according to the quadratic Equation 6 (41, 42), in which F_rel is the measured relative fluorescence, F₀ is the fluorescence measured in the absence of ligand, F_inf is fluorescence at infinite ligand concentration, [E₀] is the total enzyme subunit concentration, [P₀] is the total PLP concentration, and K_I is the dissociation constant of the equilibrium E + P ⇋ E·P, as shown in Scheme 1A.

$$F_{\text{rel}}=F_0+\left(F_{\inf }-F_0\right)\times \frac{\left[P_0\right]+\left[E_0\right]+K_I-\sqrt{{\left(\left[P_0\right]+\left[E_0\right]+K_I\right)}^2-4\left[P_0\right]\left[E_0\right]}}{2E_0}$$ (Eq. 6)

In the stopped-flow experiments, the PLP and PNPOx concentrations were comparable; thus, pseudo-first-order conditions could not be met. Under these conditions, the data in Fig. 5A were fitted to the following,

$$y={\alpha }_F\frac{1-e^{-k_{F}t}}{1-\omega e^{-k_{F}t}}-{\alpha }_S{e}^{-k_{S}t}+{\alpha }_B$$ (Eq. 7)

which was tailored to account for the observed biphasic time courses and where the α and k values are the amplitudes and observed rate constants, respectively, of the fast (F) and slow (S) phases, and α_B is the equilibrium baseline fluorescence. The first term of Equation 7 represents the time course of a second-order reaction under nonpseudo-first-order conditions (43). k_F is given by Equation 8, which describes the dependence of the observed rate constant on PLP concentration, and ω is a dimensionless parameter (with values −1 < ω < 0) measuring the deviation of the system from pseudo-first-order conditions (43); k_on and k_off are the second-order binding and first-order dissociation rate constants, respectively (Fig. 5B).

$$k_F=\sqrt{k_{\text{on}}^2{\left(E_0-\left[PLP\right]\right)}^2+k_{\text{off}}^2+2k_{\text{on}}^2{k}_{\text{off}}^2\left(E_0+\left[PLP\right]\right)}$$ (Eq. 8)

The second term of Equation 7 accounts for the decay of the PNPOx-PLP complex as discussed under “Results” (Scheme 2).

Author contributions

R. C. and F. M. planned the experiments. A. B. performed steady-state kinetics and equilibrium experiments. A. B. and F. M. performed rapid kinetics experiments. M. L. D. performed site-directed mutagenesis experiments. R. C., A. T., and F. M. analyzed the experimental data. I. N. and C. N. carried out protein purifications. A. T., F. M., and R. C. wrote the paper. R. C. designed and coordinated the overall research project. All authors revised the manuscript.