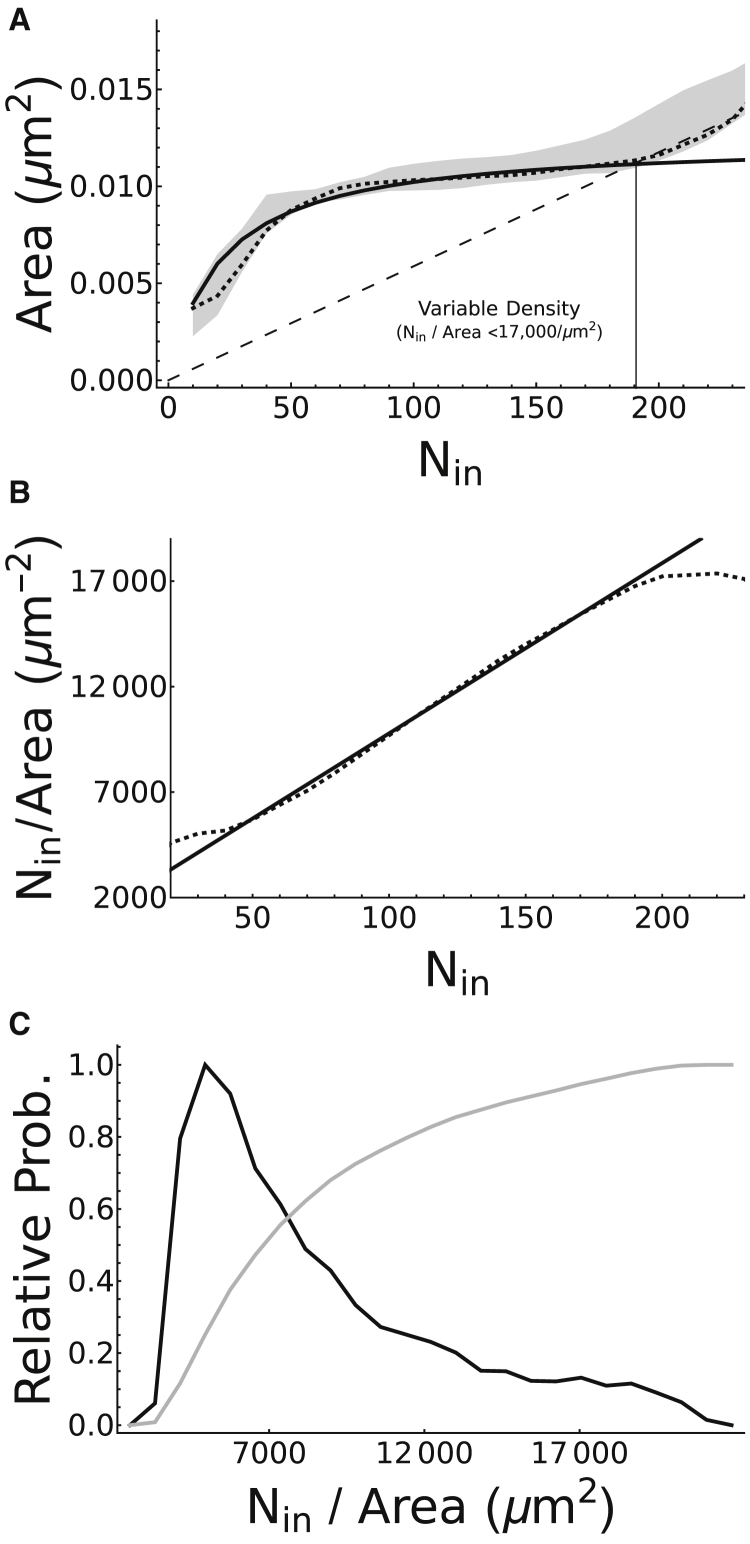
Figure 2.

(A) Inferred relation between NA area A and its integrin content N_in as determined by conditional expectation analysis. Bayesian inference is used to determine an empirical relation between A and N_in under the assumption that NAs are circular. After digitizing the distributions of NA diameters and their integrin contents published in (18), a relation between them is quantified. A 99.95% confidence interval is plotted in gray, demonstrating that the data generally exhibits a nonlinear relation between the two variables. The maximal a posteriori (MAP) estimate of this relation is also plotted as a dotted line, suggesting that NA area depends sigmoidally on N_in for small adhesions, whereas this dependence is linear for large adhesions (compare to dashed line). The nontrivial A-nullcline of the model, describing the relation between the two variables near equilibrium as defined by Eq. 2 (solid line), is fitted to the MAP estimate in the nonlinear phase and found to be in agreement. (B) The computed integrin density inside the adhesion, N_in/A(N_in), is given. Estimates are computed from the data-derived MAP estimate of A(N_in) (dotted line) and from the model prediction for A(N_in) given by Eq. 2 (solid line). Both curves exhibit a linear increase in integrin density with respect to N_in for N_in ∈ [50, 190]. (C) The probability distribution of integrin densities is shown. Black line: probability density function P(N_in/A) = P(N_in)[d(N_in/A(N_in))/dN_in]⁻¹, where A(N_in) is given by Eq. 2; gray line: cumulative density function.