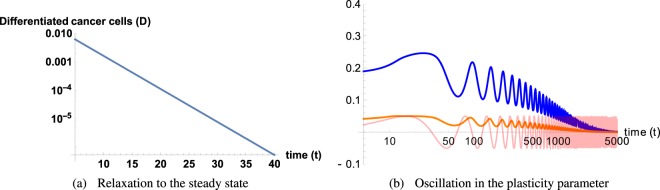
Figure 7.

In (a) Relaxation to the steady state value of differentiated cell population D near the stable point ${ℱ}_1$ with Runge-Kutta algorithm. Initial concentration {S(0), D(0), m(0), a(0)} = {0.1, 0.1, 1.0, 1.0}. With such initial parameters, the system is in the basin of attraction of the first fixed point, so of tumor extinction. The S concentration (not represented here) follows the same lines. Time is in the unit of the mitotic rate of S cells, see Section (Methods). In (b)CSCs and DCs (orange and blue respectively) oscillate with a delay with respect to the oscillating activity q₀(t) (light red curve). DCs need CSCs to differentiate, causing a delay in their productions. Likewise, CSCs need DCs to dedifferentiate. Other values of ω and ε have been tested, without obtaining any substantial difference but a time scale.