Figure 6:

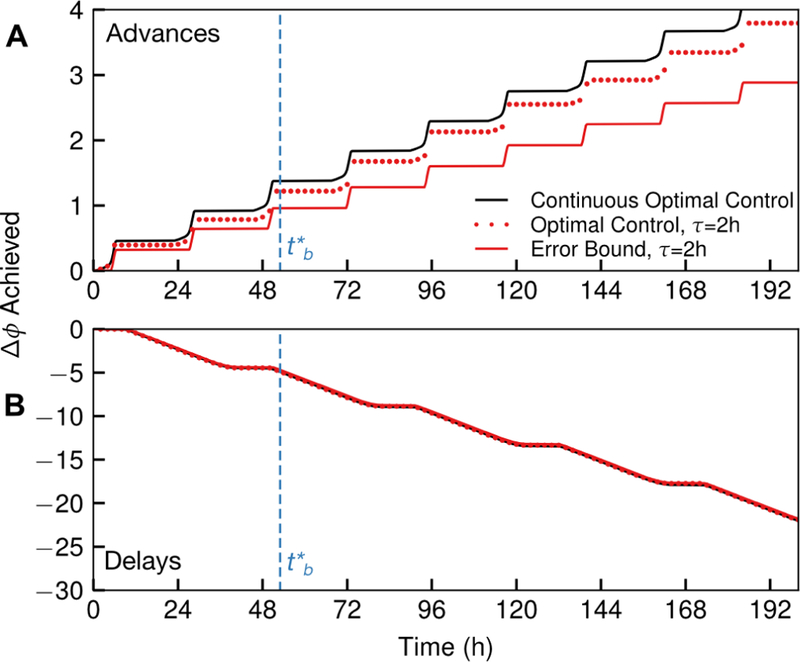
The phase shift accumulated in the continuous-time optimal control (black line) plotted as a function of time, in comparison to the lower bound on phase shift accumulated (red line) and the actual discrete-time phase shift accumulated (red dots), for τ = 2 h and ϕ₀ = 0. The residual phase error is the difference between the continuous time optimal control and the actual discrete-time control. Phase advances (A) and delays (B) are shown explicitly. The bound deviates further from the optimal control at each completed cycle, however, only the shifts that occur before $t_B^{\star }$ (dashed line) are attempted under the optimal control policy. Additionally, the error is more severe for phase advances, due to the relatively smaller positive region of the ipPRC, the fact that phase advances incur zero crosses more rapidly due to shortening the period, and the proximity of that positive region to a large negative region. For panel (B), these lines are nearly on top of one another. The numerically-calculated optimal control for τ = 2 h indeed obeys the bounds derived in Theorem 1 from the continuous time optimal control.