Figure 7:

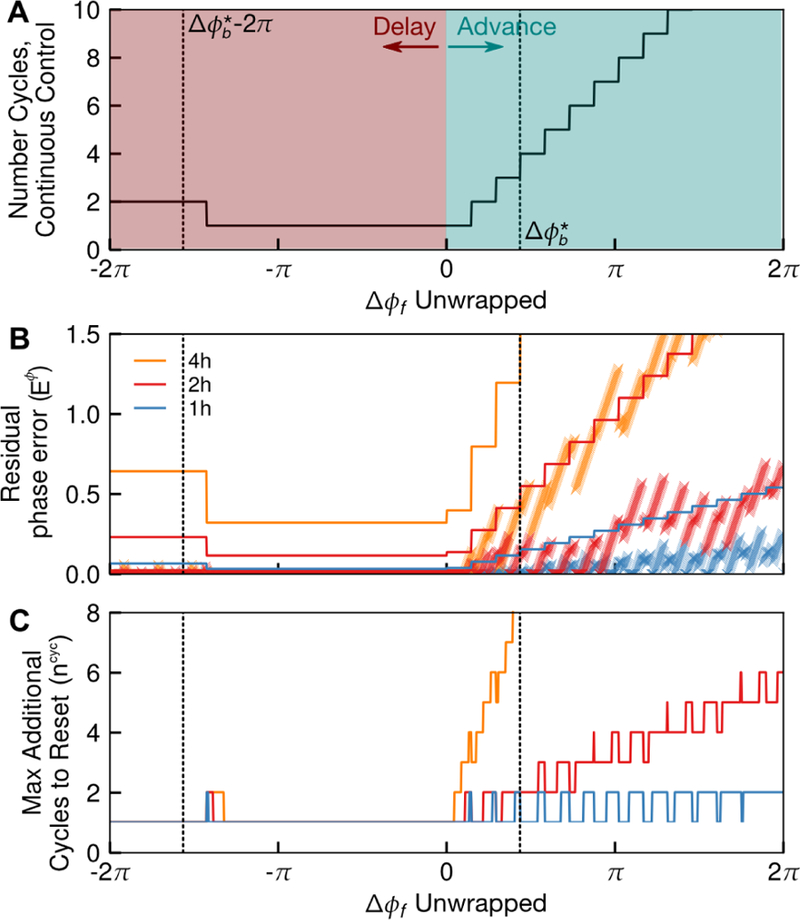
Sampling time τ affects circadian phase resetting for optimal control with evenly-spaced switching times, a common feature of feedback control and MPC. (A) Plot of number of cycles required to achieve each phase advance or delay under continuous-time optimal control. Errors due to switching timing occurs where the ipPRC crosses 0, and thus is residual phase error is a function of the number of cycles required for continuous-time optimal control. (B) A bound on $E_{\tau }^{\varphi }$, the distance to the nal phase that will remain at $t=t_f^{\text{opt}}$ under optimal control with a constant sampling time is derived from the continuous optimal control trajectory. Here, the derived bound is shown as a line, and the $E_{\tau }^{\varphi }$ for numerically calculated optimal control solutions are shown as x markers for each τ (plotted as discrete points for ease of visualization). The residual phase error in each case indeed obeys the theoretical bounds. (C) A bound on ${\text{n}}_{\text{cyc}}^{\text{add}}$ is also derived. For this example, 1 h and 2 h shifts yield similar residual phase error and allow a complete reset in at most two additional cycles, under ∆ϕ_b = ∆ϕ^⋆. Thus, either is a reasonable choice for sampling time, though a 2 h sampling time will reduce the cost of sampling by half. Alternately, if this drug were used only to achieve phase delays, a 4 h sampling rate would be similarly suitable.