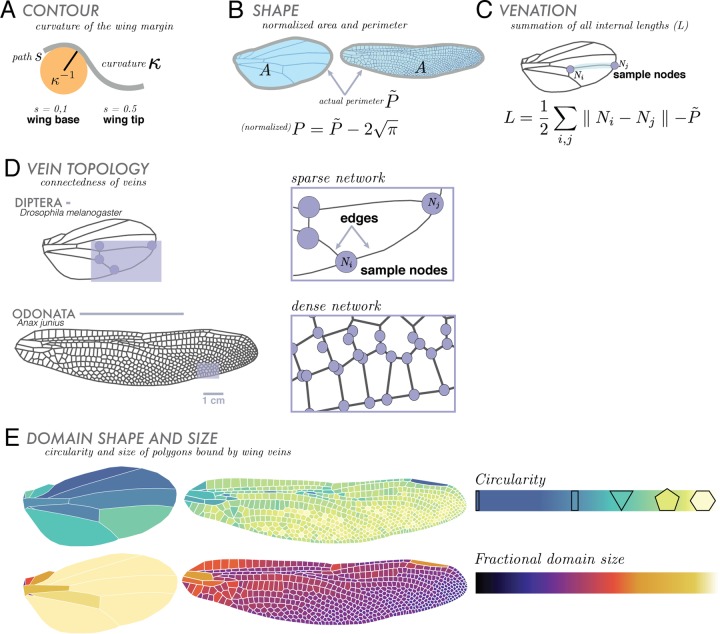
Fig. 2.

Overview of morphometric approaches. We focus on broad comparative geometric and topological components, illustrated here using Diptera (Drosophila melanogaster) and Odonata (Anax junius) wings as examples. For geometric features, we analyze curvature, shape and area, and internal venation. (A) Contour, κ, is given by the radius of curvature or κ⁻¹ (where s is arc length along the wing). (B) Shape: all wings are normalized to have an area equal to that of a circle with an area of unity (removing absolute size effects). Wing shape is characterized by its scaled perimeter, P, where P˜ is the actual perimeter of the wing. (C) Venation is treated as a network, and quantified in terms of the sum of its total internal length, L, where N_i and N_j are representative nodes. (D) We continue analyzing venation using topological measures the wing is represented as a network of vein junctions (nodes) and the lengths of vein between them (edges). Lastly, we observe the geometries and distributions of vein domains. (E) Domains, vein-bounded regions, are characterized by their circularity (shape relative to that of a circle) and fractional domain size (domain area relative to area of entire wing). These internal shapes can range from tenths of a millimeter to several centimeters.