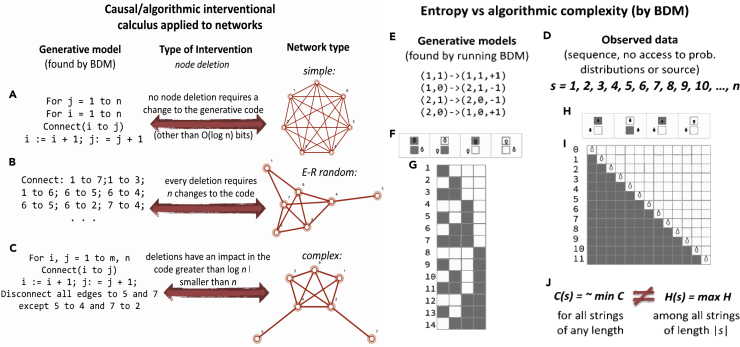
Figure 1.

From Statistical Correlation to Algorithmic Causation

(A–C) Graphs of different origin require different encodings capable of recursively generating each graph, interventions to the graph may or may not have an effect on the candidate algorithmic models depending on their algorithmic causal content. (A) A simple graph represented by a short code. (B) A random graph requires a longer code of about the same size as the graph itself in number of bits. (C) Most graphs are between these extremes namely complex graphs that neither are represented by shortest descriptions nor by the longest but in between.

(D) A sequence such as s cannot be characterized by measures based on Entropy or classical statistics, but it can be characterized as of low algorithmic complexity because more than one-third of all possible Turing machines with two states encode a decimal counter and are thus many small computer programs that encode a highly algorithmic sequence that may not have any statistical regularity (called the Champernowne constant, s has been proven to be Borel normal and thus of maximal Shannon Entropy).

(E) Shows a generative model of a Turing machine rule table able to generate the output of a counter that may underlie the sequence of natural numbers.

(F–I) (F) A computer program whose halting criterion is to reach the next leftmost head position of the Turing machine and (G) respective space-time evolution whose output in binary reproduces the sequence s in decimal. (H) A unary non-halting computer program that computes s directly followed by (I) its space-time diagram effectively encoding the sequence generating function f(x) = x + 1.

(J) It is thus clear that while Entropy H(s) can diverge from algorithmic (Kolmogorov-Chaitin) complexity C(s), it is C(s) encoding the simplicity of s and therefore characterizing its causal mechanistic nature by way of having been found by a procedure based on what will be described and exploited in this paper at the heart of the causal interventional calculus.