Figure 2.

Representations and Dynamical Systems

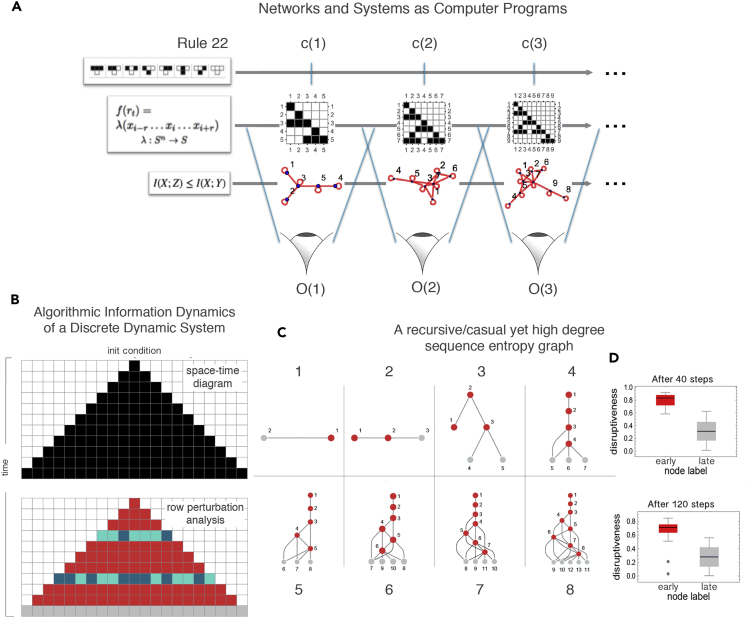
(A) The causal calculus being introduced can help reveal the generating mechanism of a discrete dynamical system, regardless of the different lossless representations it may have, that is, representations that preserve (most of) the information of the system from which it can be reconstructed in full. This ability comes from the property of closed deterministic systems that must preserve their algorithmic complexity along its time evolution given that its generating mechanism is always the same at every time step except for the time index that can be encoded by only log(n) bits. This means that any deviation from log(n) indicates that the system is not closed or not deterministic and is thus possibly interacting with some other system for which we can identify its interacting elements by perturbing them and measuring their deviation from log(n).

(B) A one-dimensional evolving system displays the same information elements determining the different causal regions after an instantaneous observation following a perturbation analysis. In a Cellular Automaton, after two random row perturbations, the algorithmic calculus reveals which rows have been artificially perturbed, with gray cells showing the identified neutral row, the last (top-down) in the dynamic evolution, indicating the time direction of the system. See Figure 3.

(C) Unlike (A), Entropy is not invariant to different object descriptions. Shown here is a tree-like representation of a constructed causal network with low algorithmic randomness but near maximum Entropy degree sequence (Supplemental Information 8), a contradiction, given the recursive nature of the graph and the zero Shannon entropy rate of its adjacency matrix, diverging from its expected Shannon entropy.

(D) Latest nodes in the same graph depicted in (C) are identified by their neutral nature, revealing the time order and thereby exposing the generating mechanism of the recursive network.