Reassessment of the Basis of Cell Size Control Based on Analysis of Cell-to-Cell Variability

Abstract

Fundamental mechanisms governing cell size control and homeostasis are still poorly understood. The relationship between sizes at division and birth in single cells is used as a metric to categorize the basis of size homeostasis. Cells dividing at a fixed size regardless of birth size (sizer) are expected to show a division-birth slope of zero, whereas cells dividing after growing for a fixed size increment (adder) have an expected slope of +1. These two theoretical values are, however, rarely experimentally observed. For example, rod-shaped fission yeast Schizosaccharomyces pombe cells, which divide at a fixed surface area, exhibit a division-birth slope for cell lengths of 0.25 ± 0.02, significantly different from the expected sizer value of zero. Here, we investigate possible reasons for this discrepancy by developing a mathematical model of sizer control including the relevant sources of variation. Our results support pure sizer control and show that deviation from zero slope is exaggerated by measurement of an inappropriate geometrical quantity (e.g., length instead of area), combined with cell-to-cell radius variability. The model predicts that mutants with greater errors in size sensing or septum positioning paradoxically appear to behave as better sizers. Furthermore, accounting for cell width variability, we show that pure sizer control can in some circumstances reproduce the apparent adder behavior observed in Escherichia coli. These findings demonstrate that analysis of geometric variation can lead to new insights into cell size control.

Significance

Cells control their size by homeostatic mechanisms. Two prevalent modes of control have been identified: sizer (in which cells always divide at a fixed size) and adder (in which cells always add a fixed size increment). These are distinguished experimentally by measurements of cell size at birth and division. Here, we evaluate the methods used in rod-shaped cells to distinguish these modes. Current methods using only cell length as a proxy for size can lead to inappropriate conclusions. Our work demonstrates that improved methods accounting for variations in cell width and cell geometry will facilitate reassessment of cell size control mechanisms in many cell types.

Introduction

Cell growth and cell division are coordinated during the cell cycle such that the size of a cell is maintained around a target value specific for each organism and cell type. However, how this outcome is achieved is still largely an open question. Investigations of cell size control intrinsically require a quantitative experimental approach, with many investigations focusing on the simple geometries of yeasts and bacteria. In fission yeast, analyses of individual cells show that they grow to a surface area of ∼165 μm² before entering mitosis and dividing (1). Phenomenological characterization of size homeostasis, measuring birth and division sizes of individual single cells, has shown that cells grow to a specified size regardless of birth size. These findings suggest that these cells monitor their own size, dividing at the same size regardless of the size at birth (2, 3, 4). This principle is called sizer control. On the other hand, the same analysis of Escherichia coli data reveals that these cells appear to add a constant size increment during each cell cycle (5, 6), so-called adder control. These cells show a positive correlation between size at birth and size at division (2, 7), so that shorter (longer) cells tend to divide shorter (longer). Theoretical studies have further investigated adder control in terms of robustness to stochastic perturbations and their consequences for the duration of different cell cycle phases (8, 9).

The interpretation of these measurements assumes an unambiguous correspondence between the observed behavior (slope of the linear regression of division size versus birth size) and the underlying basis of size control. No correlation (zero slope) implies cells with pure sizer control; a slope of +1 implies cells with pure adder control. However, experimental data have revealed slopes that lie in between these two cases, results that have challenged the notion of a simple basis for size control. As a result, controversies over the basis of size control persist even in E. coli (5, 10, 11), as well as in budding yeast (sizer versus adder (12, 13)), whereas a recent study has proposed a combination of a timer (fixed time duration cell cycle) and an adder for Caulobacter crescentus (14). Because of its stereotypical shape and greater available understanding, this work considers fission yeast as a reference model. Even in this case, the measured division-birth slope is significantly different from zero, casting some doubt on the sizer hypothesis (15).

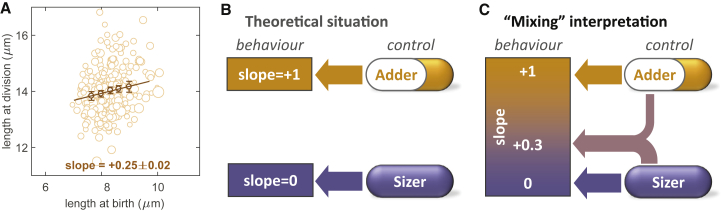
Previous work showed that size homeostasis in fission yeast is based on total-surface-area sensing (rather than on cell length or volume sensing) (1, 16). Quantitative measurements support the idea that this surface-area control is achieved by phosphorylation and accumulation of Cdr2 in protein clusters (“nodes”) in a cortical band around the nucleus. The dynamics of these processes is sufficiently fast such that an effective steady state is reached at a given cell size, with the accumulated amount of nodal Cdr2 proportional to cell volume. Furthermore, because the nodal area is of approximately constant width in cells of different lengths and radii, the Cdr2 local nodal density scales with volume/radius or as cell surface area. This area-dependent local density of Cdr2 can then, in principle, trigger mitosis via thresholding (1, 16). Moreover, through use of a cdr2-T166A rga2Δ mutant, cell size homeostasis was successfully switched to length-based size control, confirming the key role of Cdr2 protein in the mechanism (1). Critical to these conclusions were analyses of mutant cells with altered widths, using rga2Δ (thinner) and rga4Δ (fatter) mutants (1, 17, 18), which allowed for a robust distinction to be made between size controls based on length, area, or volume. However, most data from the literature use length as the measure of cell size (3, 4, 15) and for wild-type (WT) cells show a significantly positive division-birth slope (approximately from 0.2 to 0.3), suggesting that cells might inherit and preserve some elements of size information from the previous cell cycle, similar to adder behavior. Our data (Fig. 1 A) show a similarly positive division-birth slope of around 0.25. Clearly, these findings are not straightforwardly consistent with pure sizer control (1).

Figure 1.

Mapping between cell behavior and underlying basis of size control. (A) Division-birth correlation for WT (FC15, n = 256) based on measurement of cell length. The size of circles is proportional to cell radius. Binned data, with mean value ± standard error, are also shown (dark circles), together with best-fit line with indicated slope. (B) Theoretical assumption of a one-to-one mapping between division-birth slope and size control, in which slope = 0 implies sizer control and slope = +1 implies adder control. No intermediate values for the slope are expected. (C) Slope values between 0 and +1 could be interpreted as a mix between sizer and adder control (or an imprecise sizer or imprecise adder).

This nonzero slope raises the possibility that cells may display pure size control that is obscured by measurement errors or other sources of variability (Fig. 1 B). Alternatively, cells might adopt an imprecise implementation or some “impure” mixture of adder and sizer controls (Fig. 1 C). To test these possibilities, we sought to determine what division-birth slopes would be generated by pure sizer (or adder) control if the relevant sources of variation were properly accounted for. Our first result is that we can explain all the division-birth slopes experimentally observed for fission yeast in terms of pure sizer control only. Experimentally measuring a geometrical measure of cell size (length) that is different to that intrinsically used by the cells in their size control (area), together with radius variability within the cell population, can generate a large shift of the division-birth slope to higher values. We surprisingly found that a reduction in size-sensing precision by the cell or in the precision of placement of the division plane can paradoxically appear to generate better sizer behavior in a division-birth plot. These insights also apply to size control in E. coli, indicating that our approach may improve the assessment of cell size homeostasis control in many cell types.

Materials and Methods

Image acquisition and analysis

Most images analyzed here are taken from our previous publication (1). Z-stack high resolution images, used to obtain cell segmentation at different resolutions by binning pixels (Figs. 2 and 3; Figs. S1 and S2), were acquired in this study with the same protocol and equipment as in (1). This allowed us to study the effect of the segmentation error. In these cases, we applied the following new semiautomated algorithm to the images acquired at the best z-plane. We first drew manually an approximate cell axis that connected the two cell tips (A and B; see Fig. S1 A). For this preliminary manual part of the segmentation, the Fiji ImageJ tool was used (19). The AB distance was a first estimation L of the cell length. A first estimation of the cell radius was calculated as follows. From the middle point M of the AB segment, we derived an intensity profile along the direction orthogonal to the axis (toward both lateral borders of the cell; red dashed line in Fig. S1 A). The steepest gradient of this signal identified the border of the cell, i.e., the cell radius. We repeated this gradient procedure using neighboring points of M (at a distance k·dx, with k = −3, −2, …, +2, +3, and where dx is the pixel size). The average of all these values gave our first estimation of the radius. We then shortened the segment AB by this amount from both ends. This defined the new segment A′B′. We divided this segment into n equal parts (n = 0.5L/dx) by placing n − 1 internal points. The gradient procedure we used for the middle point M was then applied to all these points and to the two extremal points A′ and B′. This identified the lateral borders of the cells. The symmetry axis of the resulting lateral borders was taken to be the new symmetry axis of the cell (segment CD). From both extreme points C and D, we derived the intensity profile along the different radial directions (from 0 to 180°, steps of 2°; purple dashed line in Fig. S1 B). Ideally, the distance of the cell border to the CD segment should always have been equal to R for every point from C to D. However, cell irregularity and imaging defects altered this width. Therefore, after calculating the width from a point x_i, if the difference between this width and the width from the previous point x_{i − 1} was bigger than a given threshold (0.1 μm), we set the width equal to the width from x_{i − 1}. The final result was a set of points that described the cell border. From these points, we derived the cell length as the maximal distance between two points of the set (Fig. S1 C). The cell radius was defined as the average of its value at different positions along the CD segment, i.e., excluding the two cell tips (Fig. S1 C). Surface area and volume were then calculated using simple geometrical equations. As showed by Eq. 2 in Results, segmentation error (i.e., high image resolution) is not critical in case of calculation of the division-birth slope based on length measurements (Figs. 1 and 4; Figs. S3, S5, and S6). In these cases, phase contrast images were first analyzed by a deep neural network machine learning algorithm (20): this methodology generated binary images for feature (outline and cytoplasm) identification. These contours were then used for traditional gradient segmentation in Morphometrics (21). This procedure is fully described in (1). Strains used in the experiments are listed in Table S2. All codes were implemented in MATLAB 2017b (The MathWorks, Natick, MA).

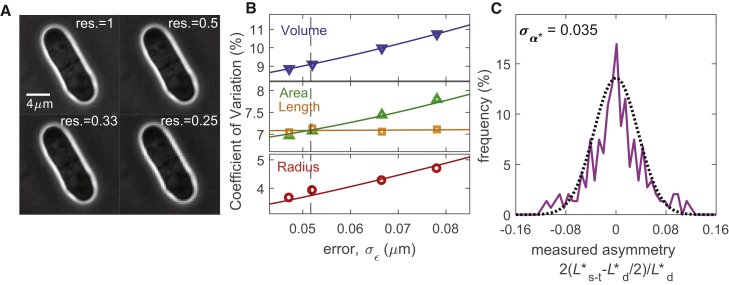
Figure 2.

Model parameter estimation. (A) Reduction of image resolution by pixel binning. Reported value of resolution is res = 1/n (where n × n pixels have been averaged and condensed into a single pixel; res = 1 is the experimentally acquired image). (B) Measured CVs at division (symbols) at four different image resolutions (as in A) and therefore with four different experimental errors σ_ε. Lines show fitting of these CV data by tuning the parameters of the model. See also Fig. S2. Dashed line is located where σ_ε = Rσ_ρ: for smaller errors, area sensing becomes apparent, i.e., ${\text{CV}}_{A_d^{*}}<{\text{CV}}_{L_d^{*}}$. WT strain FC15, n = 326. (C) Measurement of division asymmetry and its fitting with a Gaussian distribution to determine σ_α (n = 106), where L^∗_s-t is the measured distance between the division septum and cell tip. Experimental data are fitted with σ_α^∗ = 0.035. Because ${\sigma }_{\alpha \ast }^2\approx {\sigma }_{\alpha }^2+\left(5{\sigma }_{\epsilon }^2/L^2\right)$, we can extract σ_α = 0.032.

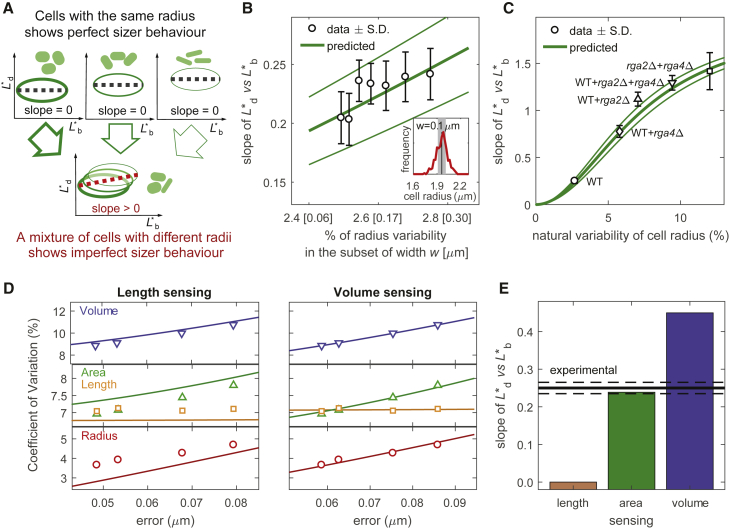
Figure 3.

Fission yeast implements a pure area-based sizer. (A) Intuitive explanation for how, for area sensing, variability in cell radius causes deviation from perfect sizer behavior. Ellipses represent cloud of data points and dashed lines their linear fitting. (B) Inset: radius distribution in red and example of selection of cells with radius in range of ± w = ± 0.1 μm around the mean value (gray shadow). Main plot: each black circle is obtained with a different value of w; for a given w (value in squared brackets on x axis), division-birth slope for length is measured on subset of selected cells (black circle, slope ± SD), and radius variability is measured (Eq. S5; Fig. S4B). Predicted slope based on area sensing is calculated with Eq. 2 as a function of radius variability (green curve ± SD, calculated by additively decreasing or increasing parameter values up to 1%; for example, σ_α changes from 2.2 to 4.2%). This curve is a zoom of that reported in C. (C) Predicted area-based (green curve ± SD) and measured division-birth slope for length (mean value ± SD) obtained by combining mutants with different radii. (D) Fitting of the observed CV at division (symbols) by tuning the parameters of the model (curves), at different image resolutions and therefore different experimental errors, σ_ε. Left panel shows length-sensing model. Right panel shows volume-sensing model (see also Table S1). (E) Bars report the theoretical values of division-birth slope for length for each possible geometric size-sensing model (based on length, area, or volume). Area sensing is the one that provides the best agreement with the experimental data (black line ± SD, continuous and dashed lines). (D) uses the same data as in Fig. 2B. For all other panels, data are from automated segmentation: rga2Δ (FC2947, n = 208), WT (F15, n = 256), and rga4Δ (FC1901, n = 170).

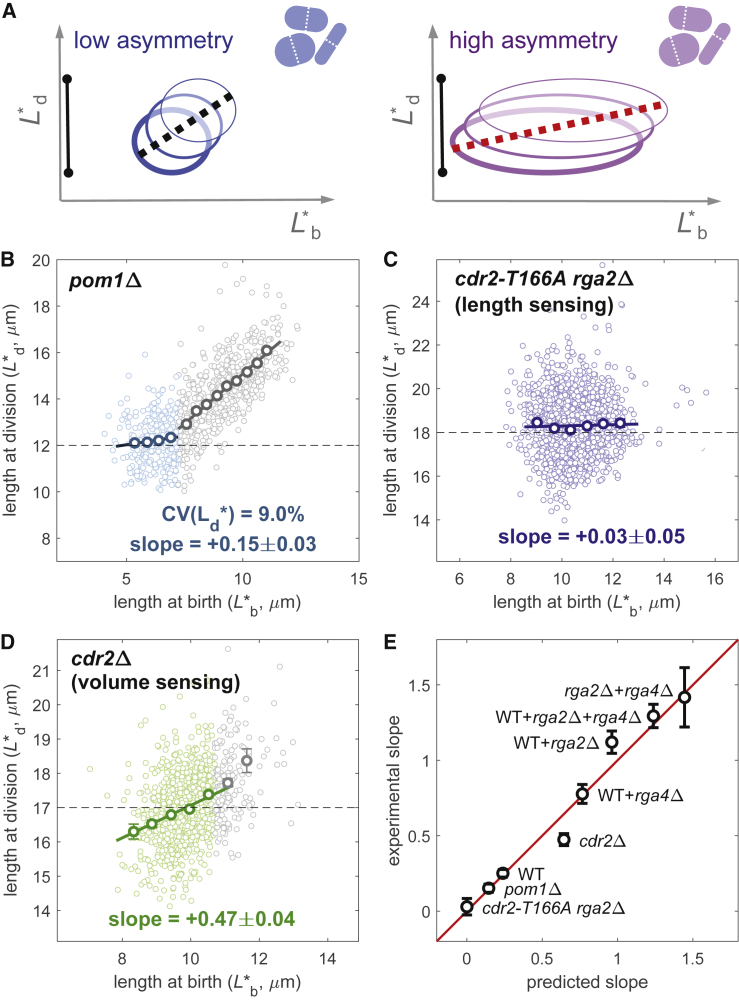
Figure 4.

Counterintuitive predictions arising from asymmetric division errors and consequences of length or volume sensing. (A) Possible explanation of how an increase in the asymmetry error at division brings the birth-division slope closer to zero. Black bars indicate the width of the distribution of the division length. (B) Size homeostasis plot for pom1Δ (FC2063, n = 1757, data from (1)). Slopes of reported fit lines are +0.15 ± 0.03 for the sizer regime (light blue color, length at birth less than 7 μm) and +0.86 ± 0.03 for the adder/timer-like regime (gray color, length at birth greater than 7 μm). In the sizer regime, division length has a CV of 9.0%, higher than the WT, but a lower birth-division slope (+0.15 vs. +0.25 for the WT as reported in Fig. 1A), as predicted by the model. (C) Size homeostasis data for the cdr2-T166A rga2Δ mutant that implements length sensing show near-perfect sizer behavior (FC3218, n = 1785, data from (1)). (D) Size homeostasis data for the cdr2Δ mutant, which implements volume sensing. Regression line and reported slope of +0.47 ± 0.04 refer to the binned data with length at birth smaller than 10 μm (green color). Cells with length at birth greater than 10 μm (gray color) show a slope of +0.88 ± 0.16 (FC3161, n = 1046). Binned data (with mean value ± standard error) shown as bold circles in (B)–(D). (E) Summary of the agreement between experimental slopes and values obtained by the model. Data points show the mean value ± standard error (see also Fig. S6B).

Results and Discussion

Sources of variation and mathematical model

To improve our understanding of the variety of size homeostasis behaviors, we developed a simple mathematical model of pure area-based sizer control in fission yeast, including the relevant sources of variation in cell size regulation and measurement (Supporting Materials and Methods). Because a sizer mechanism is based on size sensing only, the model does not contain time as a variable, and, therefore, we do not need to include any error in the duration of the cell cycle. We aimed to test whether such a model is sufficient to reproduce the apparently imperfect sizer behavior observed above. We assumed that each source of variation is Gaussian-distributed, with the free parameters being the following standard deviations (SDs): σ_μ (error μ that cells make in sensing size and therefore in mitotic commitment), σ_α (error giving asymmetric placement α of the division plane with respect to the exact midplane of the cell) and σ_ρ (natural cell-to-cell variability ρ of the radius). We also included σ_ε as the SD of the measurement error ε (μm) due to image acquisition and segmentation (see Table 1 for the entire list of variables and parameters of the model). As an example, the measured cell radius (R^∗, where in the following, the mark ^∗ will denote a measured quantity) is given by R^∗ = R(1 + ρ) + ε, where R is the mean radius of the cell population (see Supporting Materials and Methods). Similar expressions can also be derived for the length at birth and length at division. From these equations, we can calculate the coefficient of variation (CV) for all geometrical quantities at division (Supporting Materials and Methods). For instance, for the case of a sizer attempting to attain a cell surface area A at division, the CV of the division length $L_d^{\ast }$ is given at lowest order by the sum of three contributions:

$$\text{C}{\text{V}}_{L_d^{\ast }}\approx {\left[{\sigma }_{\mu }^2+{\sigma }_{\rho }^2+{\left(\frac{2\pi R}{A}\right)}^2{\sigma }_{\epsilon }^2\right]}^{\frac{1}{2}}.$$ (1)

Table 1.

Variables and Parameter Values of the Model

Symbols	Description	Units	Value for Each Strain
			WT	pom1Δ (subset of short cells only)	cdr2-T166A rga2Δ	cdr2Δ	E. coli
ρ, σρ	Gaussian random variable with SD σρ (value reported here) describing cell-to-cell radius variability	%	2.7	2.7	2.7	2.7	3.5
μb, μd, σμ	Gaussian random variables with SD σμ (value reported here) describing cell error in sensing its size	%	6.5	8.6	6.5	6.5	6.5a
α, σα	Gaussian random variable with SD σα (value reported here) describing the asymmetry in division, defined as $\left(2L_{s-t}^{\ast }-L_d^{\ast }\right)/L_d^{\ast }$, where $L_{s-t}^{\ast }$ is measured distance between the division septum and cell tip.	%	3.2	3.2	3.2	3.2	3.2a
εb, εd, σε	Gaussian random variables with SD σε (value reported here) describing experimental error in the measurement at different resolutions res = 1 (0.0635 μm/pixel), res = 0.5 (0.127 μm/pixel), res = 0.33 (0.190 μm/pixel), and res = 0.25 (0.254 μm/pixel)	μm	0.045 (res=1)	0.06b	0.06b	0.06b	0.04b
			0.052 (res=0.5)
			0.067 (res=0.33)
			0.078 (res=0.25)
R	Mean cell radius	μm	1.96	1.89	1.58	1.95	0.55
L	Target cell length at division in case of length sensing (mean of the experimental measurement)	μm	n.a.	n.a.	18.3	n.a.	n.a.
A	Target cell area at division in case of area sensing (mean of the experimental measurement)	μm2	164	158	n.a.	n.a.	n.a.
V	Target cell volume at division in case of volume sensing (mean of the experimental measurement)	μm3	n.a.	n.a.	n.a.	183	3.77
q	Persistence of the cell radius from birth to division	n.a.	0.72	0.72	0.72	0.72	0.72

n.a., not applicable.

^aSimulations with additively increasing/decreasing each SD by up to 1% (or 2%) are reported in Fig. S7.

^bEstimation based on the resolution of the images.

Compared to simple probabilistic sizer models for which cells divide according to a probability of division as a function of cell size (12, 22), our equation describes the distribution of sizes at division as a combination of well-defined sources of error. The same holds for the other CVs:

$$\text{C}{\text{V}}_{R^{\ast }}={\left[{\sigma }_{\rho }^2+\frac{{\sigma }_{\epsilon }^2}{R^2}\right]}^{\frac{1}{2}},$$

$$\text{C}{\text{V}}_{A_d^{\ast }}\approx {\left[{\sigma }_{\mu }^2+\left(\frac{1}{R^2}+\frac{4{\pi }^2{R}^2}{A^2}\right){\sigma }_{\epsilon }^2\right]}^{\frac{1}{2}},$$

and

$$\text{C}{\text{V}}_{V_d^{\ast }}\approx {\left[\frac{A^2{R}^2{\sigma }_{\mu }^2+\left(A^2{R}^2+16{\pi }^2{R}^6-8\pi A{R}^4\right){\sigma }_{\rho }^2+4\left(A^2+5{\pi }^2{R}^4-4\pi A{R}^2\right){\sigma }_{\epsilon }^2}{A^2{R}^2+\frac{16}{9}{\pi }^2{R}^6-\frac{8}{3}\pi A{R}^4}\right]}^{\frac{1}{2}}.$$

Parameter estimation

We first estimated the model parameters. All parameters, except for the noise σ_α due to asymmetry in division, were obtained by fitting to the measured CV of radius, length, area, and volume at division (which are all clearly unaffected by σ_α). We utilized images of WT cells acquired at different z-planes (to guarantee good focus). We then generated (and resegmented) images at four different resolutions, i.e., with different values of the experimental error σ_ε. This was achieved by binning a square of n by n pixels into a single pixel, with n ranging from 1 to 4, i.e., four different values of σ_ε (Fig. 2 A). Cells were then segmented using an algorithm specific for rod- or quasi-rod-shaped cells (Materials and Methods). For each of the four geometrical quantities (radius, length, area, and volume) and for each resolution, we measured the CV at division. We then fitted these data points with the CV equations reported above by tuning the six model parameters (σ_μ, σ_ρ, and the four values of σ_ε). The minimal root mean-square deviation was obtained with σ_μ = 6.5% and σ_ρ = 2.7% (Figs. 2 B and S2). Finally, through measurement of the localization of the septum, we directly estimated the asymmetry in division in WT cells. By knowing σ_ε, we obtained the value of σ_α = 3.2%, consistent with literature reports (Fig. 2 C; (23)).

From the above estimation, we note the value of 6.5% for the area-sensing error, which is smaller than the CV of the division length (∼7–8%) normally used to indicate the accuracy of size sensing (4). This initial result indicates that the sizer mechanism in fission yeast is slightly more precise than previously thought.

Furthermore, for area-based size sensing, one would naively expect that the CV of area at division $\left(A_d^{\ast }\right)$ should be smaller than that for length $\left(L_d^{\ast }\right)$, i.e., ${\text{CV}}_{A_d^{*}}<{\text{CV}}_{L_d^{*}}$. Our data in Fig. 2 B show that this is only true for sufficiently small experimental measurement errors σ_ε. This is again expected because errors in measurement affect the area calculation more than for length because radius only enters the area estimation. Only when σ_ε is sufficiently small (σ_ε < Rσ_ρ, as predicted by the model; see Supporting Materials and Methods) does area sensing emerge as being less variable.

Alteration of cell radius variability supports pure sizer control

Most of the analysis reported in the literature on rod-shaped cells is based on length because length is the easiest quantity to measure and because length is clearly affected by genetic and physiological perturbations. Therefore, it is important to find an appropriate way to interpret the outcomes from such measurements. In this case, our data for the WT alone show a positive birth-division slope: 0.25 ± 0.02 (Figs. 1 A and S3), consistent with available values (3, 4, 15). We next investigated whether these discrepancies were due to errors and whether these data could support the existence of pure sizer control in fission yeast.

From the expressions of the measured length at birth $\left(L_b^{\ast }\right)$ and measured length at division $\left(L_d^{\ast }\right)$, while still having underlying area-based size control, we can derive an equation for the theoretical value of the division-birth slope (Supporting Materials and Methods):

$$\mathrm{slope}\left(L_d^{\ast },L_b^{\ast }\right)=\frac{2{\sigma }_{\rho }^2}{H^2{\sigma }_{\rho }^2+K^2},$$ (2)

where $H^2=1-\left(4\pi R^2/3A\right)$ and $K^2=\left({\sigma }_{\mu }^2+{\sigma }_{\alpha }^2\right)/[1-\left(4\pi R^2/3A\right)]+{\left(4\pi R/A\right)}^2{\sigma }_{\epsilon }^2/[1-\left(4\pi R^2/3A\right)]$. The expression defines a sigmoidal curve, with the radius variability having an important effect (Fig. S4 A). The reasons for these dependencies are as follows. For surface-area-based size control, both birth and division lengths strongly depend on the true value of the radius and on its variability from cell to cell because cells with a bigger (smaller) radius divide shorter (longer) and give birth to shorter (longer) daughter cells, like in adder control. A consequence of this correlation is a positive division-birth slope (Fig. 3 A), with a theoretical slope given by Eq. 2. On the contrary, when all the cells have the same radius (i.e., σ_ρ = 0), the true division length will be perturbed by the sensing error only and will thus be independent from the length at birth, giving a zero division-birth slope.

To verify whether radius variation can explain the observed division-birth slope based on length, we exploited the natural variability of the radius that is present in WT cells. We modulated the variability of the radii of a population of WT cells by selecting subsets with a measured radius R^∗ in the range R ± w. For a given w, we extracted the division-birth slope and radius natural variability of the selected cells (Eq. S5; Fig. S4 B). By gradually reducing w (i.e., by selecting a subset of cells with lower radius variability), the experimental division-birth slope decreased toward zero as predicted by the model without any further parameter adjustment (Fig. 3 B). We also analyzed different combinations of WT, thin (rga2Δ), and fat (rga4Δ) cells. Each combination had a different variability of the radius and, according to our analysis, therefore also a different division-birth slope for length. Model predictions, again without any further parameter adjustment, were in good agreement with the experimental data (Fig. 3 C). Overall, these results again support a pure area-based sizer control in fission yeast, in which variations in the radius cause division-birth slopes based on length to deviate far from zero.

WT data alone support area-based size control

So far, our analysis has assumed surface-area sensing for the WT strain. This assumption is based on previous experiments on WT as well as on thin (rga2Δ) and fat (rga4Δ) mutants (1, 16), showing that, regardless of the cell radius, all these strains divide at a specific surface area (of ∼165 μm²). We attempted to overcome this reliance on mutants by again exploiting the natural variability of the radius in WT cells to verify that area sensing was preserved and was not an artifact due to use of the two mutants.

Following the same procedure used for area sensing, we developed a model based on a length-sensing assumption and a model based on a volume-sensing assumption (Supporting Materials and Methods). For each of the two models, we derived expressions for the CVs at division and the division-birth slopes for the various geometric quantities (length, area, volume). As for area sensing (Fig. 2 B), the CV equations were used to estimate the parameters σ_ε, σ_μ, and σ_ρ; by tuning their values (separately for length and volume), we found the best fit for the experimental division size CVs for WT cells (Fig. 3 D). With the obtained parameter values (Table S1), the equations for the division-birth slopes were then used to calculate the theoretical value of the slopes. We found that the experimental CVs, but not the experimental WT slopes, can be reproduced by the model based on a volume-sensing assumption, whereas the model based on a length-sensing assumption was unable to reproduce either (Fig. 3, D and E). On the other hand, the model based on area sensing provided a good fit to both. These results indicate, without reliance on mutants, that fission yeast sizer control is indeed based on surface area.

Asymmetric division and defective size sensing can paradoxically appear to enhance sizer behavior

Besides experimental error and radius variability, the model also includes two further biological sources of variability: asymmetry and sensing precision. We next studied their role in size homeostasis behavior based on length measurements.

We showed above how variability in the radius can mask sizer behavior, bringing the division-birth slope based on length far from zero (Fig. 3, B and C). However, for a given value of the radius variability σ_ρ, Eq. 2 indicates that the slope decreases when the asymmetry (σ_α) or the sensing (σ_μ) error increases. This result means that increased errors in the division process (in term of septum positioning and/or size sensing) paradoxically generate better sizing behavior in a division-birth plot, with a slope closer to zero (Fig. S4 A).

These counterintuitive behaviors can be rationalized as follows: in the case of a perfect sizer, an increase in the asymmetry error does not affect the distribution of the division length. As a consequence, the cloud of points of the division-birth size homeostasis plot is stretched along the x-direction only, causing a reduction of the slope (Fig. 4 A). A bigger sensing error produces a wider distribution of both division and birth lengths, i.e., a stretch along both x- and y-directions. However, because the slope value is affected by (reduced) only by the horizontal stretch because of a wider distribution of birth lengths (Supporting Materials and Methods), this case turns out to be similar to the asymmetry case. For an increased sensing error, the wider spread of the data points reduces the statistical confidence of the slope value. Therefore, to attain similar levels of precision for the slope values as before, a higher number of segmented cells are required (Fig. S5 A).

To verify these counterintuitive predictions about the asymmetry (σ_α) or the sensing (σ_μ) error, we re-examined the case of the pom1Δ mutant cells, which divide shorter and often display asymmetric divisions as compared to WT cells (${\text{CV}}_{L_b^{\ast }}$ = 22% vs. 8.4% for the WT) (24, 25). Although formally, we cannot exclude that the pom1 deletion might induce different geometric size sensing, we assume here that pom1Δ cells still use surface area for triggering mitosis. Moreover, because of the incompressibility of the G2 phase, cells that have a length at birth above 7–8 μm follow an adder/timer mechanism rather than a sizer mechanism (4) (gray color in Fig. 4 B). Therefore, to avoid interference from this altered size control and to exclude the effects of highly asymmetric divisions, we limited our analysis to cells that start the cell cycle at lengths below ∼7 μm (light blue color in Fig. 4 B). For this subset, the CV of the division length is 9.0%, significantly higher than the WT (7.2%), indicating a higher sensing error by this mutant (estimated at σ_μ ≈ 8.6%). In agreement with the value of 0.14 predicted by the model (with SD 0.06 using additive ±1% model parameter fluctuations; for example, σ_ρ changes from 1.7 to 3.7%), the experimental division-birth slope decreases from +0.25 to +0.15 ± 0.03 (Fig. 4 B), making the mutant erroneously appear as a better sizer. For a repeat experiment on agar (Fig. S5 B) with a division-length CV of 12.2%, the model predicts a slope of 0.08 in good agreement with the experimental measurement of 0.09 ± 0.07.

Model predictions match length- and volume-based sizer control experiments

In a previous work, we manipulated fission yeast size sensing to generate Cdr2-dependent cell size sensing according to cell length, using the cdr2-T166A rga2Δ background. After this reprogramming, cell division indeed occurred based on length rather than surface area (1). According to our model for length-based size control, the division-birth slope for length should be zero regardless of the natural variability of the radius and of the segmentation error (Supporting Materials and Methods). The experimental value for cdr2-T166A rga2Δ of +0.03 ± 0.05 confirms our model prediction and provides additional support for length sensing in this mutant (Fig. 4 C).

In the same work, we showed that division in the cdr2Δ mutant is no longer controlled by area and is instead based on a secondary Cdr2-independent mechanism that moves toward volume control (1). Similar to pom1Δ, data from this mutant can be split into two regimes: a sizer-like regime at shorter cell birth lengths (less than 10 μm) and an adder/timer-like regime for longer cell birth lengths. The division-birth slope obtained for the former regime is 0.47 ± 0.04 (Fig. 4 D), which, although still (just) closer to sizer than adder behavior, is even further away from the ideal sizer behavior than the WT. Although the CV of the division length (7.0%) is similar to the WT value, an important question to answer is whether cdr2Δ is still implementing a sizer.

For a model based on pure volume sensing, we can again derive the equation for the division-birth slope (Supporting Materials and Methods). The equation and the result indicate that the effect of natural variability of the radius is bigger for volume sensing than for area sensing (Fig. 3 E). Intuitively, this result follows because cell volume has a quadratic dependence on the radius, whereas area has a linear dependence only. For this reason, the shift of the division-birth slope away from zero will be more pronounced. Without any parameter changing, the model prediction is a slope of +0.62, close to the observed value of around +0.5. Therefore, for cdr2Δ, as for all the cases analyzed in this study (Fig. 4 E), the appearance of more adder-like behavior is likely due to the use of an incorrect geometrical feature (length) and to the effect of variability in the cell radius.

Because cdr2Δ cells are more elongated, the aspect ratio (R²/A) is lower than in the WT (∼0.017 vs. 0.023). Therefore, we also examined how the aspect ratio affects the slope calculated in Eq. 2. Exploring a wide range of R and A values, the slope shows only marginal changes (Fig. S5 C), suggesting that the aspect ratio is not responsible for the higher slope observed in this mutant.

Incorporating a varying radius into the mathematical model

So far, the model was based on the assumption that cell radius does not change from birth to division. Experimental data, however, show a strong, but not perfect, positive correlation between the two measurements (slope q = 0.72, Fig. S6 A), indicating that some adjustments in the cell width might occur during the cell cycle. As an additional test, we therefore relaxed the constant radius assumption and developed a generalized mathematical model with the radius varying from R_b = R(1 + ρ) at birth to R_d = qR_b + (1 − q)R at division. These dynamics guarantee the preservation through generations of cell radius around the average value R. Numerical simulations show that the key features of the model outcomes are preserved. Moreover, because the variation of radius within one cell cycle is relatively small (Fig. S6 A), we did not find significant changes in our results. As a result, the agreement with the experimental evidence is still good (Fig. S6 B). Furthermore, by relaxing the assumption of a fixed cell radius from birth to division, this generalized model allows us to simulate a series of consecutive cell cycles. Our results confirm the ability of the sizer to (approximately) recover the ideal size within one single generation (Fig. S6 C), as expected (2, 3).

Adder behavior can emerge from pure sizer control

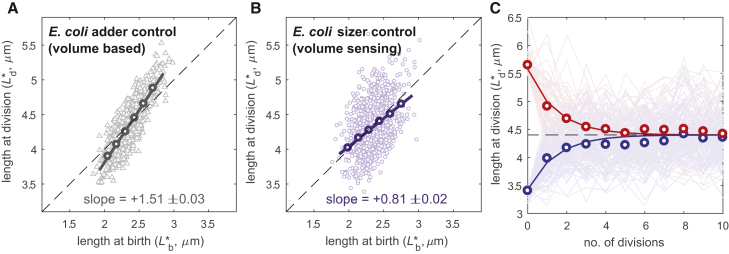
With the exception of length sensing in the cdr2-T166A rga2Δ mutant, utilizing length as the experimental size measure partially masks pure sizer behavior by moving the division-birth slope toward adder behavior, i.e., toward a value of +1. We therefore asked whether the same effect is present in a pure adder mechanism. In particular, we focus on a division-adder mechanism (11) based on cell volume as proposed for the widely studied bacterium E. coli (26), which shares the same rod shape as fission yeast. These considerations allowed us to develop a model for a pure adder (Supporting Materials and Methods). In contrast with other work (27), in our adder model, we did not include any direct errors on the time durations: rather, variation in the duration of the cell cycle is a consequence of the error in sensing the added size, which is the fundamental quantity monitored by a cell that implements adder control. Similar to our observations for pure sizer control based on volume sensing, the effect of natural cell radius variability causes a monotonic increase of the division-birth length slope from the theoretical adder value of +1 up to +2 (Fig. S7 A). By using 3.5% as an estimation of the radius variability (7, 28, 29), our adder model generates a division-birth length slope of +1.51 ± 0.03 (Fig. 5 A). Robustness of the outcome was tested by additively increasing/decreasing each SD by up to 1% (or 2%): slope values remained entirely above +1 (Fig. S7 B). However, all the experimentally reported division-birth length slopes for E. coli range from +0.7 to +1 (5, 7), i.e., they never overshoot the theoretical pure adder value. This result could suggest a potential incompatibility between an adder mechanism and the observed behavior.

Figure 5.

Radius variability and sizer control reproduce the apparent adder behavior in E. coli. (A) Simulation of division-birth slope based on length measurements for E. coli utilizing pure adder control based on cell volume (n = 3000). Dashed line represents theoretical adder behavior (slope of +1). (B) Same plot in case of pure sizer control based on cell volume. Both plots of (A) and (B) have been obtained with R = 0.55 μm, V = 3.77 μm³, 3.5% as the natural radius variability, and the same noise used for fission yeast (Fig. S7B shows the effect of perturbations of these noise values). Binned data, with mean value ± standard error, also shown (dark circles), as well as best-fit line, with indicated slope. (C) Simulation of 5000 cells over 10 generations with volume-based pure sizer control in E. coli using model with radius change from birth to division. Dim lines represent simulated single-cell data for cells dividing shorter (pale blue) or longer (pale red) than the theoretical size (dashed black line). Circles: mean length at division at each generation. Blue and red lines: division length recovery for ideal adder with no radius variability.

Our results on the cdr2Δ mutant revealed that in the case of a volume-based pure sizer, the effect of radius variability is more pronounced than in the case of area sensing and moves the division-birth length slope much closer to adder-like behavior. Running a numerical simulation of such a volume-based sizer model with σ_ρ = 3.5% (slightly higher than the radius variability in fission yeast) on E. coli-sized cells (7, 28, 29), we obtained a division-birth length slope of +0.81 ± 0.02 (Fig. 5 B), in agreement with the experimental results from this bacterium. Allowing an additive increase/decrease of the model SDs of up to 1% (for example, σ_ρ changes from 2.5 to 4.5%), the slope remains in the range of adder behavior (slope = 0.88 ± 0.19). A striking feature of adder behavior is a slow correction of the cell size after an erroneous division (too long or too short). Experimental data show that cells gradually converge to the correct length in the following four to five generations. As for fission yeast, we therefore used a pure sizer model with the radius dynamics from birth to division. Simulations of this model then reproduced the slow recovery of cell size typical of adder behavior (Fig. 5 C). The proposed volume sensing in E. coli makes radius variability more relevant in the generation of long and short cells. Therefore, to converge to the expected length, the radius needs to revert to its mean value R, which is a more gradual process requiring several generations (Fig. S6 A). These findings suggest that sizer control in E. coli cannot currently be completely ruled out.

Conclusions

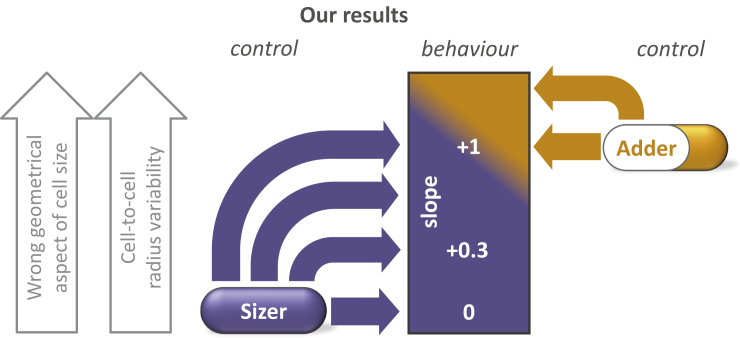
Phenomenological characterization of size homeostasis is a common approach for extracting information about cell size regulation. Although initial results previously suggested an imperfect or possibly mixed sizer-like control in fission yeast, we have shown here that pure sizer control based on accurate sensing of cell size is implemented in this organism, using a Cdr2-dependent mechanism with area-based control in the WT and length-based control in cdr2-T166A rga2Δ (1). Moreover, we have identified three generalizable aspects in the analyses of size homeostasis: 1) high accuracy in the measurement of the cell size is necessary to avoid erroneous conclusions on geometrical sensing (σ_ε < Rσ_ρ, Fig. 2 B); 2) as a consequence, use of the wrong geometrical quantity (e.g., length instead of area), combined with natural variability of the cell radius, distorts the observed size control behaviors (Fig. 3, B and C). Although this effect disappears in the presence of length-based sizer sensing (see cdr2-T166A rga2Δ, Fig. 4 C), the behavior is even more markedly perturbed when sizer control is based on cell volume (see cdr2Δ in Fig. 4 D and E. coli in Fig. 5 B); 3) asymmetric cell division and, more surprisingly, a reduction in the precision of size sensing can paradoxically appear to enhance sizer behavior. As shown by the case of pom1Δ in fission yeast, an apparently stronger sizer behavior (lower division-birth slope) may be due to a loss of precision in size control (Fig. 4 B). These demonstrations show that correct interpretation of size homeostasis behavior requires accurate measurements of multiple geometrical quantities. Furthermore, “intermediate” behavior (as in WT cells) may not necessarily be due to imperfect size control nor to a combination of two or more distinct size controls (e.g., sizer and adder). Even limited variability can move the division-birth length slope from 0 toward +1 in the case of pure sizer control and from +1 toward +2 in case of pure adder control, thus completely obscuring the underlying fundamental basis of size control (Fig. 6).

Figure 6.

Summary: how a pure sizer mechanism can show a wide range of behaviors. Noise and error lead to an increase of the slope for sizer control (and also for adder control).

An important aspect that has emerged in our analysis is the effect of radius variability. One might expect that the small variations found from cell to cell might have only a marginal effect on size control behavior. Surprisingly, the curve and data in Fig. 3 C show that, in the case of area-based sizer sensing in fission yeast, a radius variability of only 7% is sufficient to move the division-birth slope close to +1, making pure sizer control wrongly appear as a pure adder. The equations of the model allow us to understand how any particular size homeostasis behavior can emerge from antagonism between inaccuracy in the division process (asymmetry and size sensing) and radius variability. In the approximation of the slope expression given in Eq. 2, the first nonzero term is $2{\sigma }_{\rho }^2/K^2$. If we ignore the contribution of the experimental error ${\sigma }_{\epsilon }^2$, this term can be approximated by $2{\sigma }_{\rho }^2/\left({\sigma }_{\alpha }^2+{\sigma }_{\mu }^2\right)$, which clearly displays the antagonism between the two effects. In our case, the combination of the estimated values for asymmetry (σ_α = 3.2%) and size sensing (σ_μ = 6.5%) errors gives a total SD of 7.2%. Therefore, we can expect that a radius variability of the same order of magnitude can neutralize the effect of these two sources of variation and lead to adder-like behavior.

For the same reason, despite the adder phenotype, sizer control is still not completely ruled out in E. coli (Fig. 5; (10, 30, 31)). Furthermore, according to our analysis, adder control based on volume would tend to show behavior closer to a timer (division-birth length slope significantly above +1). One caveat is that our adder model considers the simple case of a constant cell size increment from birth to division. It has been alternatively suggested that a constant volume (per origin) is added between two initiations and that cells then divide a constant time after initiation (26). Furthermore, we emphasize that we cannot exclude a pure adder mechanism based on cell length (rather than cell volume as proposed in (26)). Our equations indicate that to distinguish whether the cell is sensing length or area without the use of mutants of different cell widths, the error in the measurement should be smaller than the absolute radius variability. However, because of the small radius of E. coli, this constraint is very challenging (σ_ε < Rσ_ρ ≈ 20 nm).

Overall, the analysis presented here shows that pure sizer control is able to reproduce a large variety of cell size homoeostasis behaviors. Our results, with careful attention to both sources of variation in size control and to geometrical aspects preserved by the cell, could be widely relevant in deciphering size homeostasis behavior in many cell types. Although our current models apply to rod-shaped cells only, our approach could be extended to the different geometries of other organisms. We expect to find analogous deviations from the expected theoretical behavior if the experimental measurements do not match the actual underlying geometrical quantity used by the cell for size sensing.

Author Contributions

Microscopy imaging, B.K.; image analysis, B.K. and G.F.; mathematical modeling, G.F. and M.H.; manuscript writing, G.F., F.C., and M.H.; project conception, G.F. and M.H.

Editor: Antoine van Oijen.

Supporting Citations

Reference (32) appears in the Supporting Material.