LAmbDA: label ambiguous domain adaptation dataset integration reduces batch effects and improves subtype detection

Abstract

Motivation

Rapid advances in single cell RNA sequencing (scRNA-seq) have produced higher-resolution cellular subtypes in multiple tissues and species. Methods are increasingly needed across datasets and species to (i) remove systematic biases, (ii) model multiple datasets with ambiguous labels and (iii) classify cells and map cell type labels. However, most methods only address one of these problems on broad cell types or simulated data using a single model type. It is also important to address higher-resolution cellular subtypes, subtype labels from multiple datasets, models trained on multiple datasets simultaneously and generalizability beyond a single model type.

Results

We developed a species- and dataset-independent transfer learning framework (LAmbDA) to train models on multiple datasets (even from different species) and applied our framework on simulated, pancreas and brain scRNA-seq experiments. These models mapped corresponding cell types between datasets with inconsistent cell subtype labels while simultaneously reducing batch effects. We achieved high accuracy in labeling cellular subtypes (weighted accuracy simulated 1 datasets: 90%; simulated 2 datasets: 94%; pancreas datasets: 88% and brain datasets: 66%) using LAmbDA Feedforward 1 Layer Neural Network with bagging. This method achieved higher weighted accuracy in labeling cellular subtypes than two other state-of-the-art methods, scmap and CaSTLe in brain (66% versus 60% and 32%). Furthermore, it achieved better performance in correctly predicting ambiguous cellular subtype labels across datasets in 88% of test cases compared with CaSTLe (63%), scmap (50%) and MetaNeighbor (50%). LAmbDA is model- and dataset-independent and generalizable to diverse data types representing an advance in biocomputing.

Availability and implementation

github.com/tsteelejohnson91/LAmbDA

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Amidst trillions of cells and hundreds of distinct cell types in the human body, understanding tissue heterogeneity and the resulting phenotypic consequences is a mammoth task with far-reaching impact. For example, the brain consists of diverse co-localized neural, glial, immune and vascular cell types that work in concert to form complex nervous tissues. Complex tissues and their constituent cell types have already been studied at the tissue level of resolution (Dorrell et al., 2008, 2011; Erlandsen et al., 1976; Gomori, 1939; Zhang et al., 2014). Fundamentally, these tissues are composed of intricate populations of cells; researchers are now turning to the single cell level to discern new cellular subtypes (Baron et al., 2016; Darmanis et al., 2015), which are often spatially indistinct in their tissue of origin (Kumar et al., 1999). For these reasons, there is a critical need to differentiate cells from complex tissues during sequencing.

The rapid advance of single cell RNA sequencing (scRNA-seq) enables researchers to study cell differentiation and tissue heterogeneity in various tissues, diseases and physiological states. Studies have analyzed scRNA-seq data from tissues of different species, such as mouse (Chen et al., 2017; Li et al., 2016; Zeisel et al., 2015) and human (Darmanis et al., 2015; Lake et al., 2016). Comparisons between mouse and human (Baron et al., 2016) or disease and normal (Segerstolpe et al., 2016) were carried out. Some studies directly compared human and mouse cell types from the same brain region (Johnson et al., 2016; La Manno et al., 2016). These studies are especially important if data from mouse tissues can be used to identify or fill in the missing human tissues of counterpart cell types into ‘in silico chimeric’ datasets. These integrative datasets can prove to be especially useful when human data or samples are scarce or technically infeasible to generate. However, the increased number of scRNA-seq experiments has also produced unforeseen challenges.

One such challenge arises in that each scRNA-seq dataset generates its own subtype labels for the cells, which are often derived based on unsupervised approaches (e.g. clustering), and carry intrinsic systemic biases (i.e. batch effects). These labels are often not consistent enough to be directly used across datasets/studies/species without first identifying their correspondence to each other. To overcome this challenge in combining scRNA-seq datasets from different studies, batches, platforms and species, we need to consider the following three major tasks: (i) reduce the systematic biases across datasets, i.e. batch effect correction; (ii) combine datasets for integrative clustering, i.e. mega-analysis and (iii) predict cell labels in one dataset with information from another dataset, i.e. cell classification, and identification of subtype label correspondence between datasets. It is worth noting that these three general tasks are not independent.

Among these three tasks, batch effect correction has arguably the longest tradition as it has been addressed using multiple methods for microarray (Chen et al., 2011; Diboun et al., 2006), RNA-seq (Leek, 2014; Risso et al., 2014; Ritchie et al., 2015) and now scRNA-seq data (Butler et al., 2018; Haghverdi et al., 2018; Park et al., 2018). It is even more challenging to merge scRNA-seq data of different studies, batches and species than microarray or RNA-seq due to technical and biological limitations specific to scRNA-seq such as drop out events. The commonly used method is to remove sources of unwanted variance using regression with linear models such as the process adopted by Seurat-CCA (Butler et al., 2018). Alternatively, the approach can be improved by accounting for differences in the cell populations of each dataset where only like clusters of cells [mutual nearest neighbors (MNN)] are used in the linear transformation as described in mnnCorrect (Haghverdi et al., 2018). Building on these ideas, BBKNN identifies nearest neighbor clusters and uses a connectivity graph to reduce the distances between the datasets and account for independent cell populations (Park et al., 2018).

Seurat-CCA also performs mega-analysis where multiple datasets are projected into a unified subspace. In the case of Seurat-CCA, these results are achieved with canonical correlation analysis (Butler et al., 2018). Another approach, ClusterMap, uses marker genes to identify similar cell types between datasets then projects the combined dataset into a low-dimensional representation (Gao et al., 2019). Building upon mnnCorrect, Scanorama identifies MNN, which it then uses to reduce variance between datasets resulting in a multi-dataset projection using a much more efficient algorithm (Hie et al., 2018). Harmony and RISC also use multi-dataset clustering to identify cluster similarities and ultimately linear corrections that result in combined representations for further analysis (Korsunsky et al., 2018; Liu et al., 2018). Similarly, transfer learning has also been attempted, using non-negative matrix factorization where source embeddings are applied to a target dataset with scCoGAPS (Stein et al., 2018). Transfer learning can also be applied to cell type classification.

CaSTLe uses mutual information to choose the best gene features between two datasets so that boosted decision trees, an ensemble algorithm, can predict labels in a target dataset from a source dataset (Lieberman et al., 2018). There are also neural network (NN) (Alavi et al., 2018; Huang et al., 2018; Lin et al., 2017), linear model (Pliner et al., 2019; Zhang et al., 2019) and support vector machine (Alquicira-Hernandez et al., 2018; Wagner and Yanai, 2018) classifiers designed for transfer-learning between pairs of datasets. Voting algorithms such as k-nearest neighbor have been used to classify cells (DePasquale et al., 2018; Kiselev et al., 2018; Wagner and Yanai, 2018; Wang et al., 2018) and to map cell clusters between datasets (Crow et al., 2018; Kiselev et al., 2018). Clustering approaches, which employ Gaussian mixture models, have been used to calculate cluster similarity between the labeled subtypes in disparate datasets (Boufea et al., 2019; Mereu et al., 2018). At a high level, most of these methods include a step to transform the raw expression data into a generalizable representation. Due to the NN architecture that allows for non-linear projection into low-dimensional space and the early success of NNs in single-cell data analysis (Lin et al., 2017), we believe transfer learning via NNs gives us the most generalizable framework where batch effect correction, mega-analysis and cell classification tasks can be addressed using the same model.

In transfer learning, NNs can be trained more efficiently and effectively on a target task when first trained on source examples (Pratt, 1993). Training on multiple datasets drawn from different distributions can reduce the amount of sample selection bias, a potential cause of batch effects, in the resulting model (Huang et al., 2006). Furthermore, unknown labels can be derived through domain adaptive training, resulting in a target task with labels (Ganin et al., 2016). In computer vision, there have been multiple studies aiming at training convolutional NNs with label ambiguity (Cour et al., 2011; Geng, 2017; Hullermeier and Beringer, 2005; Jie and Orabona, 2010).

Fortunately, recent developments in deep learning have allowed NNs to accomplish classification and identification tasks in scRNA-seq. NN models can be used for feature reduction and identifying tissue of origin (Lin et al., 2017). However, were not optimally trained to be accurate across species in a single tissue type (Lin et al., 2017) and did not carry out dataset integration with other tissues despite the data rich environment of single cell transcriptomics (Andrews and Hemberg, 2018). To take advantage of single-cell data from different sources and species, effective machine learning algorithms are needed for across species cell type mapping and gene feature reduction.

Furthermore, the current methods used for batch effect correction, mega-analysis and cell classification in scRNA-seq would be improved if the following goals were achieved:

1. Cells should be mapped to a comprehensive union of biological cell types across datasets.

2. Batch effect correction, mega-analysis, and cell classification should be replicable in a hold-out group of samples.

3. A framework should be generalizable to more than two datasets.

4. A framework should not be restricted to labels from one dataset.

5. A framework should not be restricted to a single model type.

It should be noted that in many studies, major cell type information is generally known, which reduces the search space when mapping high-resolution subtypes of cells between datasets.

From these principles and goals, in this paper we present LAmbDA (Label Ambiguous Domain Adaptation), which attempts to train a model using all datasets as input along with a combined subset of representative labels unspecific to a single dataset and possible label mappings discerned through the literature or preprocessing. The accuracy of LAmbDA is evaluated on hold-out groups of cells coming from multiple datasets. Furthermore, LAmbDA can project the hold-out group (for model evaluation) or all the cells (for mega-analysis) into a batch effect corrected low-dimensional representation. The goal of LAmbDA is to provide a framework that is highly generalizable to multiple applications (batch effect removal, mega-analysis, cell classification), to scaling (dataset number, sample size), to integrative label sets (combined labels from multiple studies) and to model (NN, random forest, ensemble, etc.).

Specifically, LAmbDA is generalizable and allows a model to be trained simultaneously on two or more datasets using a hybrid label set from one or more datasets. It takes a semi-supervised approach and is designed primarily for use on high-resolution subtypes of cells where unsupervised algorithms have reduced accuracy and capacity for knowledge transfer between datasets. Its general framework allows us to test multiple machine learning algorithms including logistic regression (LR), Feedforward 1 Layer NN (FF1), Feedforward 3 Layer NN (FF3), Recurrent NN (RNN1), Random Forest (RF) and the ensemble method FF1 with bagging (FF1bag) on multiple simulated and real datasets (e.g. human pancreas and human/mouse brain scRNA-seq datasets) for subtype identification and matching. Subtypes of cells shared across datasets are considered replicable and robust (Crow et al., 2018). We refer to these robust classes of cellular subtypes as ‘consistent’ since they are present regardless of dataset, species, and condition. These biologically relevant consistent subtypes can be discovered by LAmbDA.

To summarize, we demonstrate that LAmbDA-based models are capable of simultaneously matching unstandardized labels with varying degrees of overlap, combining disparate datasets from different species/platforms using training and testing sets, and predicting consistent subtypes of cells learned during training with high accuracy. It offers a framework to accommodate other models beyond these biological applications to suit a variety of data types and analyses.

2 Materials and Methods

2.1 Datasets

Ten datasets were used to test LAmbDA. We intentionally chose a heterogeneous mix of datasets to study the robustness of our method. The datasets include three pancreatic scRNA-seq datasets (aka pancreas), three brain scRNA-seq datasets (aka brain), two simulated datasets with one cell type difference (aka simulated 1), and two more simulated datasets with two cell type difference (aka simulated 2).

We generated two synthetic datasets using splatter (Zappia et al., 2017) with four corresponding cell types. Cell type 4 was removed from dataset B and retained in dataset A resulting in simulated 1 (Dataset A: 2000 cells and 4 cell types, Dataset B: 902 cells and 3 cell types). In simulated 2, cell type 1 was removed from dataset A and cell type 4 was removed from dataset B (Dataset A: 1190 cells and 3 cell types, Dataset B: 902 cells and 3 cell types). The pancreatic datasets included (Fig. 1A) 1 human dataset with 15 cell types (Seg, 1980 cells) (Segerstolpe et al., 2016), 1 human dataset with 10 cell types (Mur, 2126 cells) (Muraro et al., 2016) and 1 human dataset with 14 cell types (Bar, 8569 cells) (Baron et al., 2016). The brain datasets included (Fig. 1B) 1 human dataset with only neurons and 16 subtype level labels (HumN, 3086 cells) (Lake et al., 2016), 1 human dataset with neurons and glia and 6 major cell type level labels (HumNG, 285 cells) (Darmanis et al., 2015) and 1 mouse dataset with neurons and glia and 48 subtype level labels (MusNG, 3005 cells) (Zeisel et al., 2015).

Fig. 1.

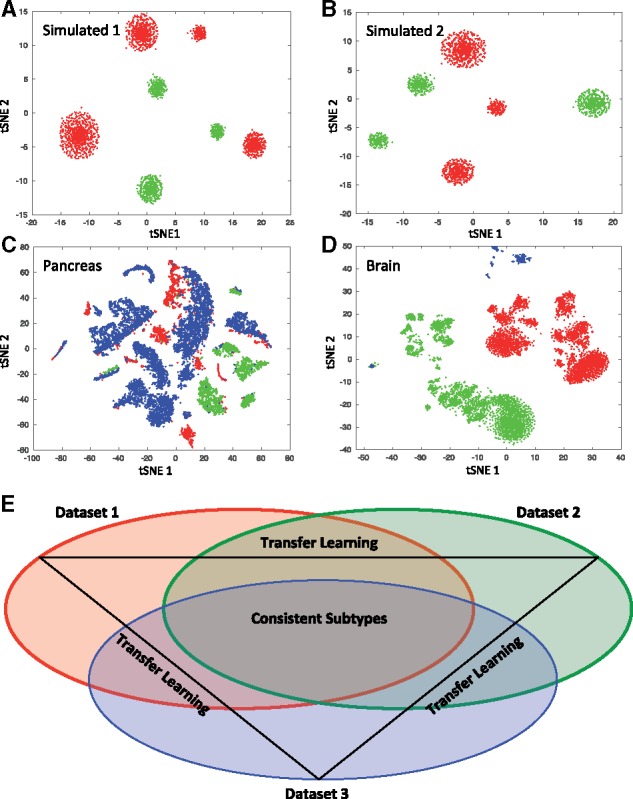
t-SNE plot of scRNAs-seq data after feature selection step. (A) Simulated 1 datasets: data A (red) and data B (green). (B) Simulated 2 datasets: data A (red) and data B (green). (C) Pancreatic datasets: Seger (red), Mur (green) and Bar (red). (D) Brain datasets: MusNG (red), HumN (green) and HumNG (blue). (E) A scheme of consistent subtype identification using transfer learning approach (a three-dataset example)

2.2 General framework

2.2.1 Dataset integration

We illustrate the LAmbDA framework using an example with three different datasets. In our notation, bold uppercase denotes matrix (X), bold lowercase denotes vector (x), lowercase letter denotes numeric value (x) and uppercase denotes a set (e.g. gene set or sample set, X). Given three scRNA-seq expression matrices ${\mathit{X}}_{\left(\mathit{i}\right)}(i=1, 2, 3),$ each with $n_i$ cells (samples) and $T_i$ transcripts (feature), the number of transcripts are first reduced to the intersection of all three datasets ($T$) based on homology across species using the Ensemble biomaRt package (Durinck et al., 2009) and gene name similar to Seurat-CCA (Butler et al., 2018). The subtype labels of each cell across all three datasets are denoted by ${\mathit{Y}}_{\left(\mathit{i}\right)} (i=1, 2, 3)$ each containing $l_i$ labels, the data matrices are:

$$\begin{array}{c}{\mathit{X}}_{(\mathit{i})}\in {\mathbb{R}}^{n_i\times t}| i=1, 2, 3;\hspace{0.17em}{\mathit{Y}}_{(\mathit{i})}\in {\mathbb{R}}^{n_i\times t}| i=1, 2, 3,\hspace{0.17em}\text{where}\\ t=\left|T\right| \mathit{where} T=T_1{\cap }^{}{T}_2{\cap }^{}{T}_3.\end{array}$$

To pool all of the datasets together for a single model, we combine the expression matrix ($\mathit{X}$) and label matrix ($\mathit{Y}$) described below:

$$\begin{array}{c}\mathit{X}=\left[\begin{array}{c}{\mathit{X}}_1\\ {\mathit{X}}_2\\ {\mathit{X}}_3\end{array}\right]\in {\mathbb{R}}^{n\times t}, \mathit{Y}=\left[\begin{array}{ccc}{\mathit{Y}}_1& 0_{n_1\times l_2}& 0_{n_1\times l_3}\\ 0_{n_2\times l_1}& {\mathit{Y}}_2& 0_{n_2\times l_3}\\ 0_{n_3\times l_1}& 0_{n_3\times l_2}& {\mathit{Y}}_3\end{array}\right]\in {\mathbb{R}}^{n\times l}\\ n=\sum _{i=1}^3{n}_i, l=\sum _{i=1}^3{l}_i.\end{array}$$

The labels are one-hot encoded such that each row of ${\mathit{Y}}_{\left(\mathit{i}\right)}$ contains a single value of one indicating the label of the specific cell. Each row will have a single value of one in the column corresponding to that subtype label. Using this encoding, it would be straightforward to train a LR, random forest or NN model ($f\left(\mathit{X}\right)$) on the data using optimization algorithms to minimize the following objective function:

$$\min \left(\mathrm{mean}\left(\sum {\left(\mathit{Y}-f\left(\mathit{X}\right)\right)}^2\right)\right).$$

However, all the labels ($L$) in the three datasets are not identical nor mutually exclusive resulting in a multi-label problem. For example, in the brain study, all interneuron subtypes in Dataset 2 could potentially match any of the interneuron subtypes in Dataset 1. This label overlap between datasets implies that a subset of the more refined consistent subtypes ($\widehat{L}$) exists in $L$ such that all subtypes in $L$ can be assigned to a subtype in $\widehat{L}$ (Fig. 1E). A new and more refined label matrix ($\widehat{\mathit{Y}}$) can be generated from $\widehat{L}$:

$$\begin{array}{l}L=\left\{k\in \mathbb{Z}\text{|}1\le k\le l\right\}\\ \exists \widehat{L}\subseteq L,\widehat{l}=\left|\widehat{L}\right|\\ \exists \widehat{Y}\in {\mathbb{Z}}^{n\times \widehat{l}}.\end{array}$$

As a result, we propose that it is possible to train a model ($\widehat{f}\left(x\right)$) on the more refined subtypes ($\widehat{L}$ and $\widehat{\mathit{Y}}$) on the following optimization problem:

$$\min \left(\mathrm{mean}\left(\sum {\left(\widehat{\mathit{Y}}-\widehat{f}\left(\mathit{X}\right)\right)}^2\right)\right).$$

The above optimization problem can be solved using the following two algorithms. Algorithm 1 corresponds to the more general version of LAmbDA used for LR and RF. Algorithm 2 corresponds to the NN implementation that actively remove batch effects in the hidden layer.

2.2.2 Algorithms

To train the LAmbDA models, we used the Adam Optimizer (Kingma and Ba, 2014) with step size of 0.01 and random mini-batches of size ${\mathit{p}}_{\mathit{batch}}$ that were changed every 50 iterations to prevent overfitting of unambiguous labels. We ran each model for 2000 iterations except for the RF model, which was run for 100 iterations. The code was written for GPU-enabled TensorFlow Python3 package. The input matrices ($\mathit{X}$, $\mathit{Y}$) were preprocessed into $\ddot{\mathit{X}}$, $\ddot{\mathit{Y}}$ and the possible inter-dataset label mappings were preprocessed into an adjacency matrix ($\mathit{G}$) before running the algorithms. For details on the preprocessing, hyper-parameter tuning and individual equations used (see Supplementary Section 2.1). The main differences between Algorithms 1 and 2 is that Algorithm 1 does not remove batch effects in a lower-dimensional representation of the cells since LR and RF do not contain a hidden layer. In contrast, Algorithm 2 is training additional loss terms to remove these batch effects in the final hidden layer before the classification layer.

Algorithm 1.

Label Ambiguous Domain Adaptation (LAmbDA) for LR and RF

Input: preprocessed expression matrix $\ddot{\mathit{X}}$, preprocessed labels $\ddot{\mathit{Y}}$, and label mask $\mathit{G}$, Supplementary Equations (S1)–(S3)

Output: a trained classifier $\widehat{f}\left(x\right)$ with mapped ambiguous labels and batch effects removed

Random initialization

1. Train on unambiguous labels Using the subset of samples that have only one possible label For the first half of total iterations:

   1. Forward propagate predicted labels
   2. Back propagate gradient from label error (i.e. update model)
2. Train on ambiguous labels Using all samples regardless of number of possible labels For the second half of total iterations:

   1. Forward propagate predicted labels [i.e. calculate $\widehat{f}\left(\ddot{\mathit{X}}\right)$, Supplementary Equations (S13)–(S17)]
   2. Assign labels to ambiguously labeled cells [i.e. calculate $\widehat{\mathit{Y}}$, Supplementary Equation (S8)]
   3. Calculate label error using $\widehat{\mathit{Y}}$ and $\widehat{f}\left(\ddot{\mathit{X}}\right)$
   4. Back propagate gradient from label error [i.e. update model, Supplementary Equations (S18) and (S19)]
3. Assigning labels to test set Using test set

   1. Assign cells to consistent subtypes
   2. Identify ambiguous label mappings using cell assignments

Algorithm 2.

Label Ambiguous Domain Adaptation (LAmbDA) for Neural Network

Input: preprocessed expression matrix $\ddot{\mathit{X}}$, preprocessed labels $\ddot{\mathit{Y}}$, and label mask $\mathit{G}$, Supplementary Equations (S1)–(S3)

Output: a trained classifier $\widehat{f}\left(x\right)$ with mapped ambiguous labels and batch effects removed

Random initialization

1. Train on unambiguous labels Using the subset of samples that have only one possible label For the first half of total iterations:

   1. Forward propagate predicted labels
   2. Back propagate gradient from label error (i.e. update network)
2. Train on ambiguous labels Using all samples regardless of number of possible labels For the second half of total iterations:

   1. Forward propagate predicted labels [i.e. calculate $\widehat{f}\left(\ddot{\mathit{X}}\right)$, Supplementary Equations (S14)–(S16)]
   2. Assign labels to ambiguously labeled cells [i.e. calculate $\widehat{\mathit{Y}}$, Supplementary Equation (S8)]
   3. Calculate Euclidean distances between subtypes [i.e. calculate $\mathit{E}$, Supplementary Equations (S9) and (S10)]
   4. Calculate label error using $\widehat{\mathit{Y}}$ and $\widehat{f}\left(\ddot{\mathit{X}}\right)$
   5. Calculate batch effects error using ${\mathit{M}}_1$, ${\mathit{M}}_2$ and $\mathit{E}$ [Supplementary Equations (S10)–(S12)]
   6. Back propagate gradient from error terms [i.e. update network, Supplementary Equation (S20)]
3. Assigning labels to test set Using test set

   1. Assign cells to consistent subtypes
   2. Identify ambiguous label mappings using cell assignments

2.3 LAmbDA model performance

We applied the LAmbDA framework with five different machine learning algorithms (LR, FF1, FF3, RNN1, RF) and one ensemble method (FF1bag) to determine the performance of the LAmbDA-based methods in cell type classification. We evaluated the performance using the following metrics: (i) test accuracy of unambiguity; (ii) cluster-wise distance ratios and (iii) Wilcoxon rank sum P-values for comparisons between labels where label ambiguity was added (in the case of pancreas and simulated data) and where the true mapping can be inferred in the original publications (in the case of brain data). For the datasets, we compare the cell classification performance with three state-of-the-art methods: MetaNeighbor (Crow et al., 2018), CaSTLe packages (Lieberman et al., 2018) and scmap packages (Kiselev et al., 2018). For dimensionality reduction, we compared with Seurat-CCA (Butler et al., 2018) and mnnCorrect (Haghverdi et al., 2018).

2.2.3 Unambiguous label accuracy

The test set accuracy of unambiguous labels was calculated from the difference between the unambiguous labels and the one-hot predicted labels averaged across each round of cross validation. The weighted accuracy (W-Acc) was generated from the mean of each of the individual label accuracies so that each output label was equally weighted regardless of the number of cells in each label. We also calculated the area under the receiver-operating curve (AUC) for unambiguous labels. The AUCs (for each output label) were averaged to give the final AUC reported in the figures and tables.

2.2.4 Distance ratios to measure batch effects

Three cluster-wise median distance ratios were calculated based on relevant combinations of labels (subtypes) and datasets. The data in these combinations consisted of the Euclidean distances between subtypes of cells in the last hidden layer of the NN implementations of LAmbDA. These combinations were: same dataset-same subtype (${\mathit{Dat}}^{+}{\mathit{Sub}}^{+})$, which was not used because this is a trivial case that had Euclidean distance =0.0; same dataset-different subtype (${\mathit{Dat}}^{+}{\mathit{Sub}}^{-}$); different dataset-same subtype (${\mathit{Dat}}^{-}{\mathit{Sub}}^{+}$) and different dataset-different subtype (${\mathit{Dat}}^{-}{\mathit{Sub}}^{-}$). For each of the combinations, the median Euclidean distance was calculated from the distances in that group. These median distance values were used to generate three ratios for comparison, (i) ${\mathit{Dat}}^{-}{\mathit{Sub}}^{+}/{\mathit{Dat}}^{+}{\mathit{Sub}}^{-}$ (theoretically <1); (ii)${\mathit{Dat}}^{-}{\mathit{Sub}}^{+}/{\mathit{Dat}}^{-}{\mathit{Sub}}^{-}$ (theoretically <1) and (iii) ${\mathit{Dat}}^{+}{\mathit{Sub}}^{-}/{\mathit{Dat}}^{-}{\mathit{Sub}}^{-}$ (theoretically = 1, i.e. control). These ratios measured the reduction of dataset batch effects [(i) and (ii)] as well as the level of noise introduction by LAmbDA (iii).

2.2.5 Assignment of ambiguous labels

The label mask [$\mathit{G}$, Supplementary Equation (S1)] used in the pancreas datasets had ambiguity added to the label mapping to determine if LAmbDA-FF1 can assign correct labels to the cell types. Specifically, incorrect label mappings were added to the training mask [$\mathit{G}$; Supplementary Equation (S1)]. In simulated 1 all three labels from dataset B could be assigned to any of the four output labels. For simulated 2 two of the input labels, one from dataset A and one from dataset B, could be assigned to any of the four consistent labels. In pancreas, five endocrine labels could be assigned to any of the five consistent endocrine labels, acinar and ductal cells could be assigned to either acinar or ductal consistent labels, and three endothelial and immune cells could be assigned to any of the three endothelial and immune consistent labels. In brain, five cortex pyramidal input labels could be assigned to eight consistent pyramidal labels. Since we could infer the likely mapping between the MusNG and HumN cortical pyramidal cells from past research, we knew the most likely mapping between them (Lake et al., 2016). These inferred high likelihood mappings were used as further validation. Wilcoxon rank-sum tests were used to measure if LAmbDA-FF1 correctly assigned ambiguous labels to the correct labels in simulated 1, simulated 2, pancreas and brain test cases. Specifically, the number of cells in correct mappings was compared with the number of cells in incorrect mappings using the Wilcoxon rank-sum test. We highlighted the ambiguous label mappings as numbered boxes in the resulting confusion matrices produced by these analyses.

2.2.6 Comparison with the related methods

We compared LAmbDA with scmap, CaSTLe and MetaNeighbor for cell classification and label mapping [Task (iii)]. Each method approached cell classification differently, so our comparisons were conducted accordingly. CaSTLe and scmap perform pairwise comparisons; therefore, we used the largest pancreas dataset Bar (8569 cells, 14 labels) to predict the smallest but most diverse dataset Seg (1980 cells, 15 labels). In brain, MusNG (3005 cells, 48 labels) were used to predict HumN (2086 cells, 16 labels). MetaNeighbor predicts the cell label using all of the labels from all datasets. In pancreas this meant 12 675 cells across 38 labels, and in brain 6376 cells across 70 labels. Since simulated 1 and 2 each only contained two datasets, no special consideration is needed to perform comparisons. The unambiguous accuracy was defined as the accuracy during cross validation on the source dataset. The Wilcoxon rank-sum tests were calculated for the same cross dataset comparisons as LAmbDA using cell label counts (used to generate weighted accuracy W-Acc) and AUC (Bradley, 1997).

Furthermore, we compare LAmbDA to Seurat-CCA and mnnCorrect in the batch effect correction [Task (i)] and mega-analysis [Task (ii)]. For simplicity, we treat these tasks similarly and calculate the same distance ratios used to compare LAmbDA model types on the aligned canonical correlation vectors from Seurat-CCA and the corrected full gene set from mnnCorrect. Since the distance ratios are not affected by the dimensionality of the data, the comparisons are fair between the hidden layer of LAmbDA, Seurat-CCA projection and the correct gene expression values from mnnCorrect. Since Seurat-CCA and mnnCorrect do not produce a model that can be applied to a hold-out group of cells, we compare LAmbDA against 20% of the cells 10 times from each dataset for Seurat-CCA and mnnCorrect despite that these cells also being used to create the Seurat-CCA and mnnCorrect correction.

3 Results

We generated simulated 1 and 2 datasets to compare the algorithm on known distributions of data as a basic ground truth. Similarly, the pancreas datasets were used to test the feasibility and performances of our methods in biological data after introducing ambiguity into the cell type labels, since the pancreas datasets were mostly unambiguous—the labels contained all major cell types with high overlaps among all three datasets. Furthermore, since all cells were from the same species, they form a good testing bed for the label mapping without the added complexity across species. The brain datasets were chosen to test the LAmbDA method capability to deal with issues such as the cross-species complexity, sample imbalance, resolution of labels and diversity of major cell types. The major cell type classes (e.g. neuron, glial) were labeled in brain too. Therefore we knew the possible subtype mappings in the brain, which served as the ground truth when the performance was evaluated. To evaluate the performance, the batch effects on the unprocessed data had to be analyzed as a baseline. All datasets showed high batch effects, which can be observed from the t-SNE diagram (Fig. 1A–D). In this study, LAmbDA aimed at removing the batch effects and revealing consistent subtypes (Fig. 1E) while still maintaining high accuracy in predicting labels of unambiguous cells.

3.1 LAmbDA improves cell classification

Tables 1 and 2 and Supplementary Table S1 describe the performances of LAmbDA, CaSTLe, scmap and MetaNeighbor to predict unambiguous and ambiguous cell types. When the ambiguous labels were tested across datasets, LAmbDA-FF1bag and LAmbDA-FF1 had the most significant cross dataset significance tests (7/8). LAmbDA-RF achieved the highest weighted accuracies in pancreas (94%), brain (72%) and had similar accuracy to scmap in simulated 2. CaSTLe achieved the highest AUC in simulated 1 (99%) and pancreas (99%). However, CaSTLe, scmap and MetaNeighbor W-Acc and AUC were calculated from the source dataset and could have been caused by over-fitting considering the inter-dataset results (5/8 significant tests for CaSTLe and 2/4 significant tests for scmap). Furthermore, the test statistics based on AUC values for both CaSTLe and MetaNeighbor were much closer than the test statistics based on cell labels to LAmbDA-FF1 and LAmbDA-FF1bag in all tests. This suggests that CaSTLe and MetaNeighbor are useful in mapping labels between datasets but should not be used over LAmbDA in classifying individual cells between datasets. This is an important distinction. High AUC is not sufficient to show a model performs well at the multi-class classification problem but rather that the labels are correctly mapping between datasets at a cell population level.

Table 1.

Cross dataset mapping

Cross-dataset mapping Wilcoxon ranksum P-value	Simulated 1 (7–4)		Simulated 2 (6–4)		Pancreas (39–17)		Brain (70–43)
	Cell label P-value	AUC P-value	Cell label P-value	AUC P-value	Cell label P-value	AUC P-value	Cell label P-value	AUC P-value
LAmbDA-FF1bag	0.0006	0.0351	0.0005	0.0937	0.0181	0.0002	0.0175	0.0018
LAmbDA-FF1	<0.0001	0.0351	0.0002	0.0937	0.0478	0.0001	0.0130	0.0014
LAmbDA-RF	0.7611	0.0001	0.7128	0.0937	0.5150	0.0015	0.2386	0.4983
Scmap	0.0160		0.1333		<0.0001		0.3671
CaSTLe	0.0091	0.0091	0.1333	0.1333	0.0008	<0.0001	0.4688	0.0049
MetaNeighbor		0.0091		0.2727		0.0005		0.4813

Note: This table contains the significance tests used to determine the accuracies of labels assigned across datasets. Cell label indicates the cell counts in a confusion matrix across the two datasets used in the experiment. AUC indicates the AUC that was calculated for the same confusion matrix based on the label probability output. Note that AUC is based on binary labels so AUC does not give information about the algorithms ability to correctly select a single label from multiple labels. The numbers in parentheses (S to C) after each dataset show how many starting labels (S) are used as input and how many consistent labels are used as output (C) by the LAmbDA algorithm. Alternatively, the cell label column measures the ability to select the correct label and no other labels. The significance tests (Wilcoxon rank-sum) were used to test whether cell counts/AUCs were higher in the confusion matrix for correct mappings (i.e. dataset A cell type 1 and dataset B cell type 1) opposed to the incorrect mapping (i.e. dataset A cell type 1 and dataset B cell type 2). Italicized values indicate significant test statistics. Bold values indicate the best metric in that particular test across all of the methods. Gray boxes indicate areas that are not available from an algorithm.

Table 2.

Unambiguous label accuracy

Unambiguous label accuracy Weighted accuracy and AUC	Simulated 1 (7–4)		Simulated 2 (6–4)		Pancreas (39–17)		Brain (70–43)
	W-Acc (%)	AUC (%)	W-Acc (%)	AUC (%)	W-Acc (%)	AUC (%)	W-Acc (%)	AUC (%)
LAmbDA-FF1bag	90	91	94	94	88	95	66	97
LAmbDA-FF1	49	73	67	86	61	94	48	93
LAmbDA-RF	93	91	99	100	94	98	72	98
Scmap	96		99		87		58
CaSTLe	85	99	96	100	75	99	32	94
MetaNeighbor		72		69		86		75

Note: This table contains the weighted accuracy (W-Acc) and area under the receiver-operating curve (AUC) for the labels in the source dataset, i.e. the dataset from which the labels were derived, using cross validation. The numbers in parentheses (S to C) after each dataset show how many starting labels (S) are used as input and how many consistent labels are used as output (C) by the LAmbDA algorithm. Note that for scmap, CaSTLe and MetaNeighbor the weighted accuracy and AUC is calculated within a single dataset. For LAmbDA, weighted accuracy and AUC were calculated for all unambiguous labels, which may come from one or more datasets. Bold values indicate the best metric in that particular test across all of the methods. Gray boxes indicate areas that are not available from an algorithm.

3.2 Multiple LAmbDA models achieve high classification accuracy

We compared each of the six LAmbDA-based methods on the simulated 1, simulated 2, pancreas, and brain datasets separately. The LAmbDA framework is shown in Figure 2. All LAmbDA models performed more accurately than random chance (Supplementary Figs S3–S6; Table 3). The lowest unambiguous accuracy was from LAmbDA-LR in all datasets and LAmbDA-RF produced the highest weighted accuracies. For mapping ambiguous labels, the ensemble method LAmbDA-FF1bag produced the most desirable results (Fig. 3A, C, E and G). LAmbDA-FF1bag also maintained high unambiguous accuracy in pancreas data (weighted accuracy: 88%) and in brain data (weighted accuracy: 66%; Supplementary Figs S5 and S6; Table 3). The constituent model of LAmbDA-FF1bag, LAmbDA-FF1, had similar weighted accuracy to that of the more complex LAmbDA-FF3 model in the biological data (61 versus 67% for pancreas, and 48 versus 49% for brain data). However, when this complexity was increased using ensemble methods, i.e. LAmbDA-FF1bag, we saw a much greater improvement in performance compared with LAmbDA-FF3 (88 versus 67% in pancreas and 66 versus 49% in brain). With high unambiguous accuracy, these models were evaluated for their ability to remove batch effects in the data.

Fig. 2.

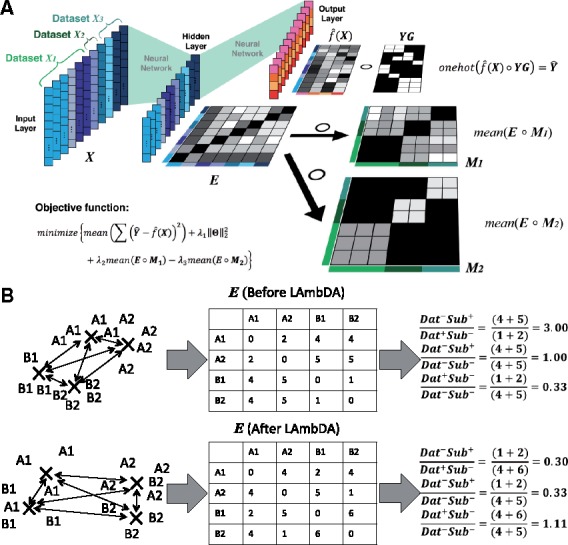
LAmbDA framework: (A) the LAmbDA framework including the simplified label mapping [Ŷ; Supplementary Equation (S8)] and batch effect removal ($\mathit{E}\circ {\mathit{M}}_1$, $\mathit{E}\circ {\mathit{M}}_2$; Supplementary Equations (S10)–(S12)] where Hadamard product ($\circ )$ denotes element-wise multiplication. (B) The distance ratios used to evaluate batch effect reduction where letter indicates dataset and number indicates subtype. The cells are in a reduced feature space in the NN last hidden layer where the distance between subtypes of cells can be measured. The first and second ratio should be <1 and the third ratio should be 1

Table 3.

The batch effect reduction measures for each of the LAmbDA models, Seurat-CCA, and mnnCorrect

	Simulated 1					Simulated 2
	Distance ratios			Accuracy		Distance ratios			Accuracy
	i	ii	iii	W-Acc (%)	AUC (%)	i	ii	iii	W-Acc (%)	AUC (%)
LAmbDA-FF1bag	0.58	0.58	0.98	90	91	0.37	0.38	0.98	94	94
LAmbDA-FF1	0.30	0.30	0.99	49	73	0.26	0.27	1.01	67	86
LAmbDA-FF3	0.84	0.90	1.01	35	62	0.86	0.85	0.99	36	66
LAmbDA-RNN1	0.86	0.84	0.97	28	52	0.88	0.77	0.84	27	53
LAmbDA-LR				27	51				26	50
LAmbDA-RF				93	91				99	100
Seurat-CCA	0.36	0.37	1.02			0.22	0.21	0.96
mnnCorrect	0.16	0.16	0.99			0.16	0.16	1.00
Full gene set	0.79	0.64	0.82			0.78	0.65	0.83
	Pancreas					Brain
	Distance ratios			Accuracy		Distance ratios			Accuracy
	i	ii	iii	W-Acc (%)	AUC (%)	i	ii	iii	W-Acc (%)	AUC (%)
LAmbDA-FF1bag	1.10	1.02	0.92	88	95	0.74	0.65	0.91	66	97
LAmbDA-FF1	0.69	0.60	0.92	61	94	0.63	0.56	0.86	48	93
LAmbDA-FF3	0.98	0.95	1.04	67	92	1.00	0.83	0.83	49	93
LAmbDA-RNN1	0.84	0.96	1.02	40	84	1.21	0.80	0.64	9	67
LAmbDA-LR				17	54				17	56
LAmbDA-RF				94	98				72	98
Seurat-CCA	0.74	0.75	1.01			0.95	1.03	1.09
mnnCorrect	0.64	0.64	0.98			0.74	0.75	1.01
Full gene set	1.30	1.02	0.78			1.16	0.84	0.72

Note: The LAmbDA models also include weighted accuracy (W-Acc) and area under the receiver-operating curve (AUC) so that bath effect reduction and accuracy can be compared. Seurat-CCA and mnnCoreect do not perform the additional prediction so they were not included. The LAmbDA results were calculated on a holdout group of cells that were not used during training. The Seurat-CCA results and mnnCorrect results are produced from the training set of cells since there is no way to conduct the analyses on a holdout group of cells. In this way, the LAmbDA to Seurat-CCA and mnnCorrect comparison is like comparing LAmbDA test accuracy to Seruat-CCA and mnnCorrect training accuracy. mnnCorrect also does not return the low-dimensional representation (it would be straight-forward using PCA or tSNE) so the corrected full gene set was used. Distance ratio i should ideally be <1.0 approaching 0.0. Distance ratio ii should ideally be <1.0 approaching 0.0. Distance ratio iii should ideally be 1.0. Italicized distance ratios correspond to improvement over the uncorrected gene set and bold represents best or tied for best performance.

Fig. 3.

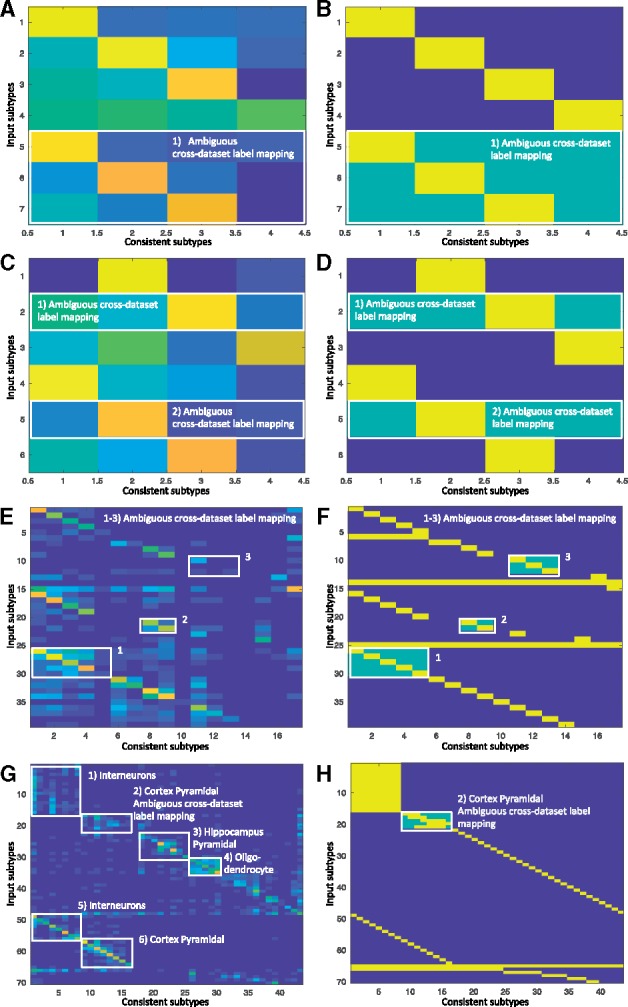
Confusion matrices with their associated label masks used during LAmbDA–FF1bag training. Each numbered white box is used to highlight patterns in the data or where labels were ambiguous. (A, C, E, F) Confusion matrix across datasets where rows are original cell types and the columns are the consistent cell types (i.e. LAmbDA output labels) for simulated 1 (A), simulated 2 (C), pancreas (E) and brain (G). (B, D, F, H) The label mask used during LAmbDA training. Yellow indicate the true labels, which were either known or inferred from the literature green indicated added ambiguity such that green and yellow constitute the label mask

3.3 LAmbDA NNs reduce batch effects between datasets

The NN-based LAmbDA-FF1, -FF1bag, -FF3 and -RNN1 each performed additional feature reduction (Table 3). During training, the hidden layer improved cellular resolution and reduced dataset batch effects as measured by cluster distance ratios (Table 3). LAmbDA-FF1 generated the best reduction of dataset batch effects compared with the other LAmbDA models (Table 3 and Fig. 4; Supplementary Figs S7–S11). In the pancreas dataset, LAmbDA-FF1, -FF1bag, -FF3 and -RNN1 were able to achieve better distance ratios than the full gene set features (Table 3; Supplementary Fig. S9) and were distinctly separated into consistent subtype clusters via Gaussian mixture models (Supplementary Fig. S10). The brain datasets contained greater batch effects and seemed dependent on the subtype signal. Despite this, LAmbDA-FF1 and LAmbDA-FF1bag still outperformed the full feature set across the distance metrics (Table 3 and Fig. 4). The datasets themselves showed differing levels of success in batch effect removal. Specifically, in the simulated data, LAmbDA-FF1 and LAmbDA-FF1bag showed considerable improvement over the full feature set (Fig. 4A–F). We also compared against current batch effect reduction techniques Seurat-CCA and mnnCorrect.

Fig. 4.

tSNE dimensionality reduction of 20% of samples taken from data before applying LAmbDA (A, D, G, J) and after applying LAmbDA-FF1 (B, C, E, F, H, I, K, L). The datasets are (A–C) simulated 1 datasets; (D–F) simulated 2 datasets; (G–I) pancreas datasets and (J–L) brain datasets. The colors indicate the dataset (A, B, D, E) dataset A (red), dataset B (green), (G, H) Seger (red), Mur (green), Bar (blue) and (J, K) MusNG (red), HumN (green), HumNG (blue). (C, F, I, L) The colors correspond to cell type (i.e. label). Note that for pancreas and brain these were simplified down to 10 general cell types (e.g. all 16 interneuron subtypes are now considered ‘interneuron’) to improve the interpretability. * in (C, F, I, L) indicates cell types that are not present in all datasets and therefore do not appear as a mosaic of all datasets in (B, E, H, K)

Overall we found that LAmbDA-FF1 outperformed Seurat-CCA in the simulated 1, pancreas, and brain test cases (Table 3; Supplementary Tables S7–S11). LAmbDA-FF1 performed comparably to mnnCorrect in both of the biological test cases pancreas and brain. Overall, LAmbDA models reduce the batch effects in the data (Fig. 4) and perform well compared with the current state-of-the-art batch effect correction methods.

3.4 High-resolution cortical neural subtypes are consistent across species

We show that the mouse cortical pyramidal subtypes map to human cortical pyramidal subtypes by their associated cortical layer (e.g. L2 cortex pyramidal cells in mouse are associated with L2 cortex pyramidal cells in human, Fig. 3G and H, Box 2). This indicates that high-resolution subtypes are consistent across species (in this case, mouse and human) and the conservation aligns with cortical layer. Because we were able to recreate known or inferred mappings, we applied the mapping from LAmbDA-FF1bag interneurons to infer consistent subtypes. These insights allowed us to hypothesize the label mapping of interneurons between human and mouse (Fig. 3G, Box 1). We observed specific subsets of mouse subtypes mapped to the human subtypes. With the biomarkers described in each of the primary sources of the data (Darmanis et al., 2015; Lake et al., 2016; Zeisel et al., 2015), we showed relevant biomarkers for the consistent interneuron subtypes (Supplementary Table S2) by intersecting the biomarker lists from the two species.

3.5 Major cell types consistent across species and dataset

Aside from the mapping of ambiguous labels across datasets, we found consistent mapping patterns between subtypes within the same major cell type. These mappings further validate our method. For example, the MusNG oligodendrocyte subtypes showed high consistency with other oligodendrocyte subtypes compared with other subtypes (Wilcoxon P-value <0.0001; Fig. 3G, Box 4). The HumNG oligodendrocytes mapped to multiple MusNG oligodendrocytes compared with other subtypes (Wilcoxon P-value <0.0001), and the HumNG astrocytes mapped to multiple MusNG astrocyte subtypes compared with other subtypes (Wilcoxon P-value <0.0001).

Cortical interneuron subtypes were highly consistent with other cortical interneuron subtypes in HumN compared with other subtypes (Wilcoxon P-value <0.0001, Fig. 3G, Box 5), and cortical pyramidal subtypes were highly consistent with other cortical pyramidal subtypes in HumN compared with other subtypes (Wilcoxon P-value <0.0001, Fig. 3G, Box 6). Such relationships were observed in the pancreas data, where immune cells clustered with one another (Fig. 4H and I;Supplementary Fig. S10). Furthermore, we found that models trained with MusNG and tested on HumN and vice versa showed the same major cell type patterns (Supplementary Fig. S2).

4 Discussion

All LAmbDA-based methods were able to predict cellular subtypes across datasets with varying degrees of success. Each LAmbDA model caters to different specific demands, with LAmbDA-FF1bag having the best overall performance. For instance, LAmbDA-FF1 performs best at correctly removing batch effects. LAmbDA-RF is most accurate at predicting unambiguous labels (e.g. within a dataset). LAmbDA-RNN1 shows desirable characteristics in integrating the datasets, but the expression input format needs to be further refined to take advantage of the recurrent architecture. These differences also display a unique pattern that correcting for batch effects translates well to generalizability but may decrease the accuracy of an algorithm on known labels. This suggests that batch effects and subtype differences are not independent of one another. This makes the problem even more difficult to separate the two types of variance, bias and cellular signal, in the data. We suggest different LAmbDA models should be considered to suit different dataset ambiguity levels and are especially important when studying the correct assignment of ambiguous labels.

These general patterns are also mirrored in the algorithms that LAmbDA was compared against. CaSTLe performed very well in multiple datasets with high accuracy, which is not surprising because CaSTLe is a form of ensemble random forest model. Two of the best models in specific cases were LAmbDA-RF (random forest) and LAmbDA-FF1bag (ensemble). scmap performed well in a number of datasets showing the utility in k-Nearest Neighbor (kNN)-based methods. This is especially convincing given the improved performance in batch effect correction once MNN was introduced by mnnCorrect. MetaNeighbor, a more straight-forward kNN approach than scmap also performed relatively well. Considering the performance of various LAmbDA models, CaSTLe, scmap and MetaNeighbor, it seems that the kNN algorithms provide good out-of-the-box across dataset accuracies, random forests provide high accuracy within datasets, NNs provide the added benefit of a low-dimensional representation (i.e. interpretability), and ensemble techniques greatly improve the classification accuracies both within and across datasets.

One focus of future improvement lies in ensemble methods (strong learners) that deliver higher performance by harnessing the unique strengths of individual models (weak learners). For instance, kNNs and MNN algorithms in general are able to correctly identify the closest matches across datasets but are not interpretable without post processing and do not achieve the highest accuracies. These label mappings can potentially be utilized as hypotheses for other machine learning models that are less robust to label ambiguity but achieve a higher accuracy on low ambiguity labels. This general idea is reflected in the brain dataset where there was less ambiguity across a large label set allowing LAmbDA-FF1bag to learn the high-resolution subtypes. In contrast, on simulated 1 and pancreas data, a more complex model like LAmbDA may not be needed to learn more broad cell types with higher levels of label ambiguity when compared against CaSTLe, scmap and MetaNeighbor. The level of resolution is an important factor in algorithm design, which is directly affected by the partial dependency between different types of variance (dataset, species, cell type, anatomic location).

The starkest reflection of this can be seen in the way that batch effects are addressed. Some methods attempt to identify similar clusters and decrease variance between these similar clusters that have been identified (mnnCorrect, LAmbDA). Others are focused primarily on the ‘mixing’ of individual cells between datasets so that the variances within disparate datasets mirror each other after being projected into a lower-dimensional space (Seurat-CCA). Again, we see that there is a trade-off between completely de novo correction like Seurat-CCA, which may lose some data structure, and in directed correction like mnnCorrect or LAmbDA, which are biased by the hypothesized cross-dataset mapping. Perhaps the best solutions lie again in various forms of ensemble methods that algorithmically weigh the advantages and disadvantages of each strategy to select the best representation of the data. These technical considerations will only increase the biological signals gleaned from the data even across datasets and species.

Not surprisingly, similar subtypes within a species tend to cluster together. For instance, in the brain, the oligodendrocyte cell types in MusNG formed a consistent group. This implies that subtypes of cells are difficult to further stratify and may consist of a joint distribution of major cell types, anatomic location, and other factors. More interestingly, mouse and human interneuron subtypes from the LAmbDA-FF1 model were mapped to each other. These matching subtypes can be considered consistent, which are identifiable across dataset and species. We used the intersection of biomarkers from the previous publications to identify these consistent subtypes.

An interesting cell mapping pattern was the HumNG subtypes tended to map to the MusNG subtypes more often than HumN, especially before batch effect removal in the full feature set. One possible reason is that HumN was single nuclei sequencing as opposed to whole cell sequencing in HumNG and MusNG, so the gene expression profiling could be quite different. This suggests that sequencing method may introduce larger batch effects than species differences, and cross-species training of models may be more feasible than once thought. Due to these considerations we believe that the general LAmbDA framework has a great deal of potential.

These direct biological applications of LAmbDA-based models on the brain and pancreas data and proof of concept in simulated data make compelling cases for the LAmbDA method. We postulate that our method can also adopt other learning algorithms such as deep learning, other distance metrics for the hidden layer to improve its dataset/species integration, and more preprocessing methods to identify the ideal label set and label mappings. We also believe that the LAmbDA framework is model-independent because of the high accuracy and batch effect removal correction by multiple tested models, thus making it ideal for incorporation with other machine learning models. Furthermore, even though scRNA-seq data were used in our study, the LAmbDA framework is not fundamentally limited to any data type, organism or disease. For instance, disparate tumor datasets could be combined to find consistent cell populations between patients, datasets and similar cancer types (e.g. grades of glioma).

The scalability of LAmbDA is immense. Since LAmbDA does not compute any pairwise correlations between samples, it could be easily scaled up to incorporate the increasing number of large Drop-seq datasets for single-cell studies. It is also worth mentioning that the core of the LAmbDA framework is a set of cost functions in Python (TensorFlow), making it ideal for others to integrate into their own workflows.

5 Conclusion

We developed a novel dataset integration and ambiguous subtype labeling framework, LAmbDA, to predict high-resolution cellular subtypes. LAmbDA also provides a framework to train NNs on multiple datasets simultaneously using labels from one or more datasets. Our algorithm addresses both label mapping and dataset batch effect issues simultaneously. We are able to perform these analyses without exact label correspondence. Our method is ideal to scale to even larger datasets. LAmbDA proves to be accurate for subtype prediction across species and datasets even at high subtype resolutions. It is model independent and capable of revealing hidden biological relationships between subtypes in disparate datasets. This can be especially useful in identifying consistent cell populations across tumors or stages. Furthermore, in theory, this method could be applied to any scalar data, which contain multiple datasets and ambiguous label mappings. LAmbDA can be integrated into existing machine learning pipelines to identify consistent labels and improve the robustness of the model to data systematic biases.