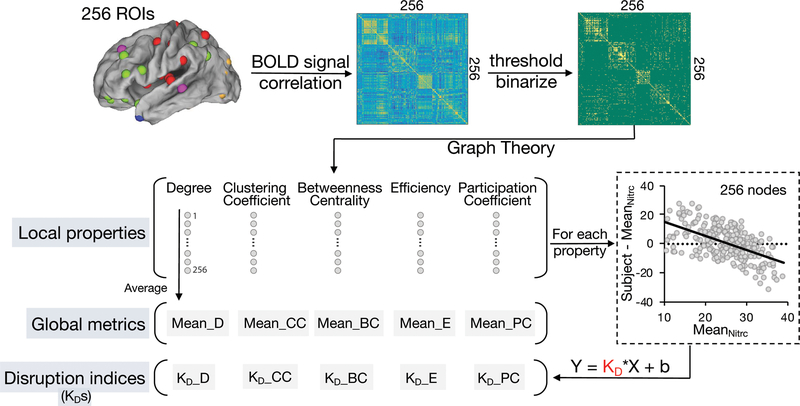
Figure 3. Calculation of graph local and global metrics and disruption indices.

For each subject in LDH-CP, LDH-HC, and off-site HC, 256 ROIs originated from 264 ROIs³⁸ (excluded 8 ROIs located in cerebellum) were used to construct ROI-based functional networks. BOLD signal of each ROI was extracted as an average over voxels within 10 mm diameter spheres centered at peak coordinates. Following this, a 256 × 256 correlation matrix was generated, showing Pearson correlation coefficient between BOLD signals. Then under each of 9 given link density (from 2 to 10%), nodal-level (local) graph properties were respectively computed using the brain connectivity toolbox (BCT)⁴². Finally, the average of each property across 256 nodes produced their corresponding global graph metrics. Meanwhile, using the mean nodal-level graph properties across 272 subjects chosen in NITRC 1000 functional connectomes project as normative topological properties, for each subject in LDH-CP and LDH-HC, firstly degree (or other graph metrics) of each node was subtracted from the mean degree (or other graph metrics) of off-site HC (n = 272) of its corresponding node, at a pre-defined link density. Following this, the difference of degree (y axis) and its corresponding mean degree of off-site HC (x axis) was plotted across all 256 ROIs. Then K_D was estimated as the slope of the fitted line. The details about calculating graph topological disruption index are expounded in 2.9.