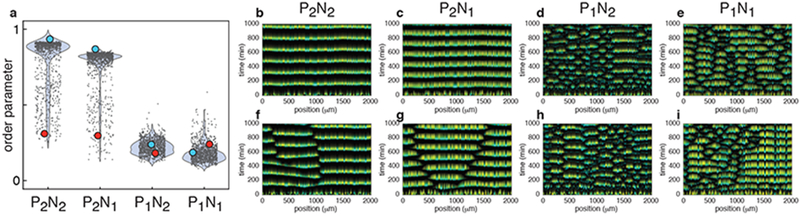
Figure 3.

The mathematical model reproduces the experimentally observed spatio-temporal dynamics exhibited by the four regulatory architectures. (a) Calculated order parameters for different initial conditions. The width of the shaded blue regions represents the empirical probability density of the distribution of the individual results (dots). The same set of 10³ random initial phases and ratios between two strains were used in simulations of all four architectures (n=10³ independent simulations for each). The order parameters for the P₂N₁ and P₂N₁ architectures were much higher than those for the P₁N₂ and P₁N₁ architectures. (b-e) Representative simulations using the same initial conditions (blue dots in (a)) that resulted in high order parameters in the P₂N₂ and P₂N₁ architectures, but not in the P₁N₂ and P₁N₁ architectures (n=10³ independent simulations for each). (f-i) Representative simulations using the same initial conditions (red dots in (a)) that resulted in low order parameters in each regulatory architecture (n=10³ independent simulations for each). Low order parameters in simulations with P₂N₁ and P₂N₁ architectures reflected the emergence of 2-3 subpopulations oscillating in anti-phase (f, g). In contrast, low order parameters reflected spatially disorganized behavior in P₁N₂ and P₁N₁ architectures (h, i).