Cooperation and spatial self-organization determine rate and efficiency of particulate organic matter degradation in marine bacteria

Significance

Microorganisms can cooperate by secreting public goods that benefit local neighbors; however, the conditions that favor cooperative growth in the environment, and the way in which this growth alters microbes’ contribution to ecosystem functions, remain unexplored. Here, we show that cooperation mediates the degradation of polysaccharide particles recalcitrant to hydrolysis in aquatic environments. Combining experiments and models, we define the physiological and environmental parameters that mediate the transition from cooperation to competition. Cooperation emerges through the self-organization of cells into ∼10- to 20-µm clusters that enable uptake of diffusible hydrolysis products. When cooperation is required, the degradation of recalcitrant biopolymers can only take place when degraders exceed a critical cell concentration, underscoring the importance of microbial interactions for ecosystem function.

Abstract

The recycling of particulate organic matter (POM) by microbes is a key part of the global carbon cycle. This process is mediated by the extracellular hydrolysis of polysaccharides, which can trigger social behaviors in bacteria resulting from the production of public goods. Despite the potential importance of public good-mediated interactions, their relevance in the environment remains unclear. In this study, we developed a computational and experimental model system to address this challenge and studied how the POM depolymerization rate and its uptake efficiency (2 main ecosystem function parameters) depended on social interactions and spatial self-organization on particle surfaces. We found an emergent trade-off between rate and efficiency resulting from the competition between oligosaccharide diffusion and cellular uptake, with low rate and high efficiency being achieved through cell-to-cell cooperation between degraders. Bacteria cooperated by aggregating in cell clusters of ∼10 to 20 µm, in which cells were able to share public goods. This phenomenon, which was independent of any explicit group-level regulation, led to the emergence of critical cell concentrations below which degradation did not occur, despite all resources being available in excess. In contrast, when particles were labile and turnover rates were high, aggregation promoted competition and decreased the efficiency of carbon use. Our study shows how social interactions and cell aggregation determine the rate and efficiency of particulate carbon turnover in environmentally relevant scenarios.

The microbial breakdown of complex polysaccharides is a key ecosystem process that enables the recycling of carbon from plant and animal detritus into global biogeochemical cycles. Polysaccharide breakdown by heterotrophic microbes is a relevant process in all ecosystems, from animal guts (1–3) to soils (4, 5) and oceans (6–8), allowing the deconstruction of complex forms of organic matter. In aquatic environments, many of these polysaccharides are packed inside particles ∼10 to 1,000 µm in diameter, and are accessible only to microbes that interact with the particle surface and secrete hydrolytic enzymes (9, 10). Particulate organic matter (POM) provides a scaffold for cells to attach to and grow in close proximity, increasing the opportunity for microbial interactions to take place (11). A particularly relevant type of interaction in this context is cell–cell cooperation, in which cells mutually benefit from being close to each other by increasing the availability of public goods such as extracellular hydrolysis products (12–14). Although numerous studies have demonstrated that this type of interaction can occur both in the laboratory and in nature, we lack a quantitative understanding of the conditions in which cooperation takes place in an environment such as the ocean, and how it can affect bacterially mediated functions such as the turnover of POM. In this article, we ask how physiological and environmental parameters create the conditions for cell–cell cooperation to take place during the hydrolysis of polysaccharide particles, and we quantify the effect of this social behavior on the turnover of POM.

The extent to which social interactions mediated by public goods change the functioning of polysaccharide-degrading microbial populations should be highly dependent on how public goods diffuse (15, 16). In a 3D aqueous environment such as the ocean, if cells are too far apart, only a minuscule fraction of the public goods are recovered by neighbors, while the rest is lost to the environment. In contrast, if cells are sufficiently proximal to each other and the resource is limiting, growth kinetics can be cooperative, meaning that the per capita growth rate is positively dependent on the density of degrader cells (14, 17). This logic suggests that cooperation could be accompanied by the emergence of spatial patterns, such as cell patches (13). If the cooperative effects in these patches are strong, critical population density thresholds might emerge below which degradation cannot support population growth (12, 13, 17, 18). Less clear is the contribution of individual cell behaviors, such as surface attachment, chemotaxis, and biofilm formation, on the ability of cells to find those critical densities by aggregating into cell patches. To begin to understand the role of social interactions in natural systems, we need to take into account the physical constraints of the microenvironment and how populations interact with these constraints through their behaviors.

To quantify the potential contribution of bacterial social interactions and spatial behavior on relevant ecosystem processes, we focused on 2 main parameters: the speed at which polymers are hydrolyzed and converted to soluble oligosaccharides, that is, the turnover rate (19, 20), and the uptake efficiency, which is the fraction of the dissolved oligosaccharide that can be taken up by cells and converted into biomass. To study the conditions that favor cooperative interactions, as well as their impact on these two functional parameters, we developed a computational and experimental model of the colonization of insoluble particulate polysaccharides by marine heterotrophic bacteria. The individual-based model (21, 22) simulates the functional traits of cells: chemotactic movement (23), particle attachment and detachment (24), the secretion and activity of enzymes (25), oligosaccharide uptake, and growth (26). The experimental system validates computational predictions in a chitin-degrading bacterial strain isolated from the coastal ocean, and clarifies the role of physiological parameters on social interactions. We leveraged the computational model to identify the physical and physiological parameters that favor the emergence of cooperative growth, and we tested some of our predictions, using our experimental model of chitin colonization. Our work demonstrates that cell–cell cooperation is critical for the degradation of complex biomaterials, implying that the degradation of recalcitrant polysaccharides can be bacteria-limited. Moreover, cell-density thresholds that determine the onset of cooperative growth depend strongly on individual-cell behavior, and in particular those behaviors that regulate the residence time of bacteria on particles.

Results

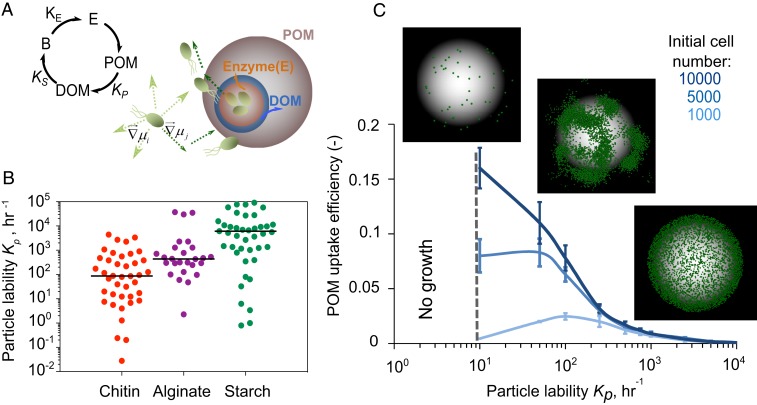
We modeled the dynamics of cell colonization, enzyme secretion, and growth (Fig. 1A), using an individual-based model to describe cells coupled to a reaction-diffusion framework to describe enzymes and oligosaccharides. In the model, bacterial cells that attached to the surface of a polysaccharide particle broadcast enzymes that reacted with the surface of the particle, releasing oligosaccharides to which nonattached cells could chemotax. Cellular uptake of oligosaccharides followed Monod kinetics (26), and cells were allowed to divide after a certain quota of oligosaccharide was consumed (22) (see Methods and SI Appendix for a detailed description and SI Appendix, Table S1 for the parameters). This individual-based approach allowed us to modulate traits such as chemotaxis or particle-attachment rate, and to measure their impact on the carbon uptake rate on a cell-by-cell basis.

Fig. 1.

POM uptake efficiency is regulated by an emergent rate-yield trade-off. (A) A schematic representation of individual-based modeling of microbial dispersal and colonization on the particle is shown on the left. A conceptual representation of the relation between the rate (K_E) of enzyme secretion by bacterial cells, the rate (K_p) at which polysaccharide substrates (POM) are broken down to oligosaccharides (DOM) by enzymes, and the uptake of oligosaccharides by bacterial cells with half saturation (K_s) is shown at right. (B) The distribution range of particle lability (K_p) from natural polymeric carbohydrates (chitin, alginate, starch). The data are for various bacterial species with their corresponding abiotic conditions (species name, substrates, and environmental conditions are represented in SI Appendix, Table S2; data are from the Brenda database: https://www.brenda-enzymes.org/). The solid line indicates the mean value of K_p. (C) POM uptake efficiency as a function of particle lability and initial population size. Dashed line indicates the no-growth zone. Microbial population assembly on the particle with 3 initial cell densities of 1,000, 5,000, and 10,000 cells are shown. Green dots show individual cells on the particle. Simulations are performed for a range of initial cell densities, and 1% detachment is allowed. Half saturation, K_s is assumed 0.1 mg/L.

A crucial parameter of our model was the particle lability, K_p, which defined how many grams of oligosaccharide were released per gram of enzyme acting on the polysaccharide surface per unit of time. K_p was a compound parameter that resulted from the product of the catalytic activity of the polysaccharide-degrading enzyme, k_cat, and the recalcitrance of the substrate. This parameter played a central role because it determined the maximum degradation rate and controlled the supply rate of carbon, the sole limiting resource, to the bacteria. A survey of hydrolysis rate values reported in the literature revealed that the particle lability, K_p, can exhibit significant variation across natural environments and microbial enzymes. K_p varied by more than 6 orders of magnitude within glycosyl hydrolase families, a trend that held true among different substrate types such as chitin, alginate, and starch (Fig. 1B). This led us to ask how variation in particle lability, K_p, affected population growth dynamics and the relationship between the rate of POM depolymerization and the uptake efficiency of released oligosaccharides.

Our results revealed that among particle-associated bacteria, the rates of depolymerization (represented by particle lability) were negatively dependent on POM uptake efficiency (Fig. 1C) (27, 28). This emergent rate/efficiency trade-off was a consequence of the diffusion of oligosaccharide in a 3D environment where soluble products that were not taken up by cells in the vicinity of the particle were lost. At high values of K_p, oligosaccharides were produced in excess of K_s, the half-saturation constant of the Monod growth function, and therefore cells approached their maximum growth rate. However, high K_p also led ∼99% of hydrolyzed oligosaccharide to be lost to diffusion (∼1% recovery), which reduced the theoretical biomass yield of the population and the POM uptake efficiency. For comparison, if the system was closed, as in a laboratory reactor, POM uptake efficiency could theoretically reach 100% because dissolved oligosaccharides would accumulate (SI Appendix, Fig. S1).

Natural environments are rarely, if ever, closed systems. Using parameters based on field measurements, our simulation supports the idea that diffusive losses are likely to limit POM uptake efficiency in the ocean (SI Appendix, Table S3). Even at the highest particle colonization densities reported from field studies, the maximum POM uptake efficiency should not exceed ∼7% according to our simulations (SI Appendix, Table S3). This number goes down to 2% if we take into account the fact that particles sink, creating a convective flow that washes away soluble oligosaccharides (29–31) (see SI Appendix, Figs. S2–S5 for simulation results with flow). Although the exact value of POM uptake efficiency depends on biological parameters such as substrate affinity (1/K_s; SI Appendix, Fig. S6), our data show that in open environments, uptake efficiency is extremely low, implying that most POM is turned into dissolved organic matter (DOM), rather than biomass. Moreover, depolymerization rate and uptake efficiency are bound to be anticorrelated due to the limited capacity of cells to take up diffusible oligosaccharides.

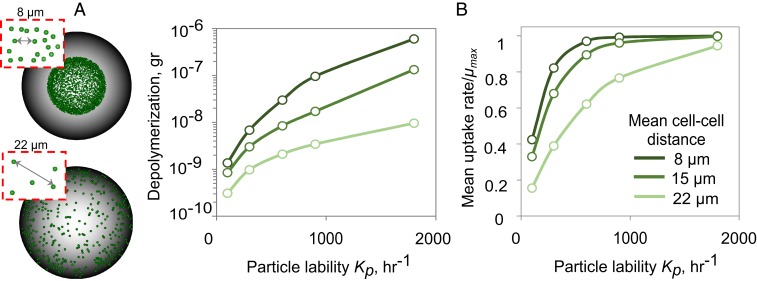
Surprisingly, we found that the high POM uptake efficiency observed at low K_p (recalcitrant particles or low enzymatic activity per cell) was mediated by the aggregation of cells into microscale patches on the particle surface, a phenomenon that was not hardcoded in the model but emerged from the interplay among diffusion, cell behavior, and growth (Fig. 1C and SI Appendix, Fig. S7). Within these patches, cells grew cooperatively by sharing oligosaccharides that would otherwise be lost to diffusion, which increased the per capita growth rate and POM uptake efficiency up to a density of 0.3 cells/µm² (SI Appendix, Figs. S8 and S9). To characterize the spatial-density dependence, we performed simulations to quantify particle depolymerization and mean growth rates as a function of the intercell distance (Fig. 2A). Our analysis showed that dense spacing (a nearest neighbor distance of 8 µm among 1-µm cells) promoted cooperation by sharing of oligosaccharides, but only when particles were recalcitrant and the oligosaccharide production rate was slow (K_p < 100 h⁻¹; Fig. 2B). More precisely, when the amount of oligosaccharide available to cells fell near K_s, the half-saturation of the Monod growth curve, an increase in the local concentration of oligosaccharide because of cell–cell aggregation, increased the per capita growth rate. In contrast, at high K_p (∼2,000 h⁻¹), oligosaccharides quickly accumulated, and the uptake rate was decoupled from the spatial organization of the cells on the particle, as there were enough resources for cells to grow at their maximal rate ([C]>>K_s; Fig. 2B). Under these conditions, there was no benefit to aggregation, and even cells spaced more than 20 cell lengths apart reached their maximum oligosaccharide uptake rate (Fig. 2B).

Fig. 2.

Patch formation on particle surface enhances the rates of polysaccharide depolymerization and breakdown product uptake. (A) The cell spatial distribution on particles for scenarios with 8- and 22-µm mean cell distances are shown. (B) Total amount of depolymerization and mean uptake rate for a range of mean cell–cell distance are represented as a function of particle lability after 10 h from start of the simulation. The simulations are initialized by placing 1,000 individual cells uniformly on the particle at the indicated mean cell–cell distance between neighboring cells. No detachment is allowed in simulations.

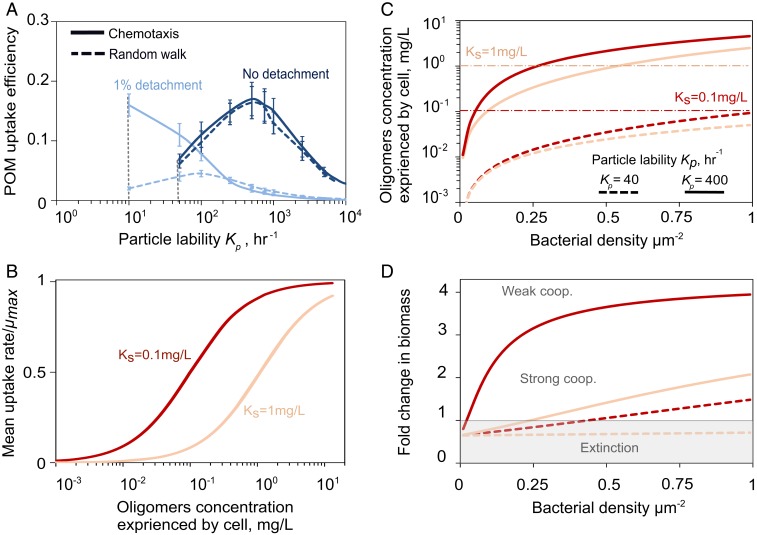
In our model, cell detachment and reattachment from the particle surface was a critical behavior that enabled the formation of patches and the degradation of recalcitrant particles. On recalcitrant particles (K_p = 10–100 h⁻¹), 1% detachment significantly increased the particle degradation rate and its uptake efficiency (Fig. 3A) and also increased the mean carbon uptake rate by a factor of ∼5 (SI Appendix, Fig. S9A) compared with a nondetaching population. Detachment allowed populations to survive on recalcitrant particles that might otherwise not sustain growth (SI Appendix, Fig. S9B). Without chemotaxis, random motility alone still allowed detaching populations to grow on more recalcitrant particles than nondetaching populations, but at ∼1/6 the maximum POM uptake efficiency (Fig. 3A) and ∼1/10 the total biomass accumulation (SI Appendix, Fig. S9B). With chemotactic motility, most cells had access to the same concentration of hydrolysis products emanating from cell patches; the distribution of carbon uptake rates for individual cells displayed a tight peak near the maximum uptake rate (µ∼0.8µ_max; SI Appendix, Fig. S9C). Our model thus suggests that detachment and chemotaxis enhance POM uptake efficiency under nutrient-limited conditions ([C]∼ K_s) by enabling the formation of patches where cells cooperate by sharing public goods.

Fig. 3.

Bacterial aggregation enhances oligosaccharide uptake rate. (A) Effects of individual cell behavior on POM uptake efficiency. Solid lines show the simulation results with chemotactic behavior, and simulations with only random walk are shown with dashed lines. Data are shown for 10 h of simulation with an initial cell number of 10⁷ cells/mL and a particle radius of 200 µm. Vertical dashed lines indicate that no bacterial growth is sustained below the indicated K_p values. (B) Mean oligosaccharides uptake rate as a function of oligosaccharide concentration modeled by Monod uptake kinetics. Two scenarios are depicted: high (K_s = 0.1 mg/L) and low (K_s = 1 mg/L) affinity. (C) The effects of bacterial cell density on the oligosaccharide release by hydrolysis, for different values of K_s (red vs. peach lines) and K_p (dashed vs. solid lines). Simulations are performed for a particle with constant radius of 200 µm and initial cell density of 0.3 cell/µm⁻². (D) Fold change in biomass as a function of initial bacterial density is shown for simulations of bacterial colonization on a single particle after 20 h. For low affinities (high K_s, peach lines) and high recalcitrance (low K_p, dashed lines) strong cooperative (strong coop.), effects emerge and a minimum cell density threshold is required for growth and degradation.

This analysis implies that the onset of cooperation is dependent on the physiology of individual bacterial strains. Strains that had either a high affinity for oligosaccharides (low K_s) or a high hydrolytic activity (high K_p) saturated their growth at low cell densities (Fig. 3 B and C), circumventing the need to cooperate through patch formation (Fig. 3D). In contrast, strains with a low uptake affinity for the public good or strains with a low per cell rate of hydrolysis (low K_p), such as those that tether enzymes to their membrane, benefitted more from cooperation with other cells and formed patches in the simulation (Fig. 3D). Therefore, cell–cell cooperation emerged during POM breakdown when the polymers were hard to degrade, either because of low hydrolytic power or poor uptake affinity. Traits such as motility, surface detachment frequency, oligosaccharide affinity, and enzyme localization determined the exact cell density threshold required for particle degradation in a given environment.

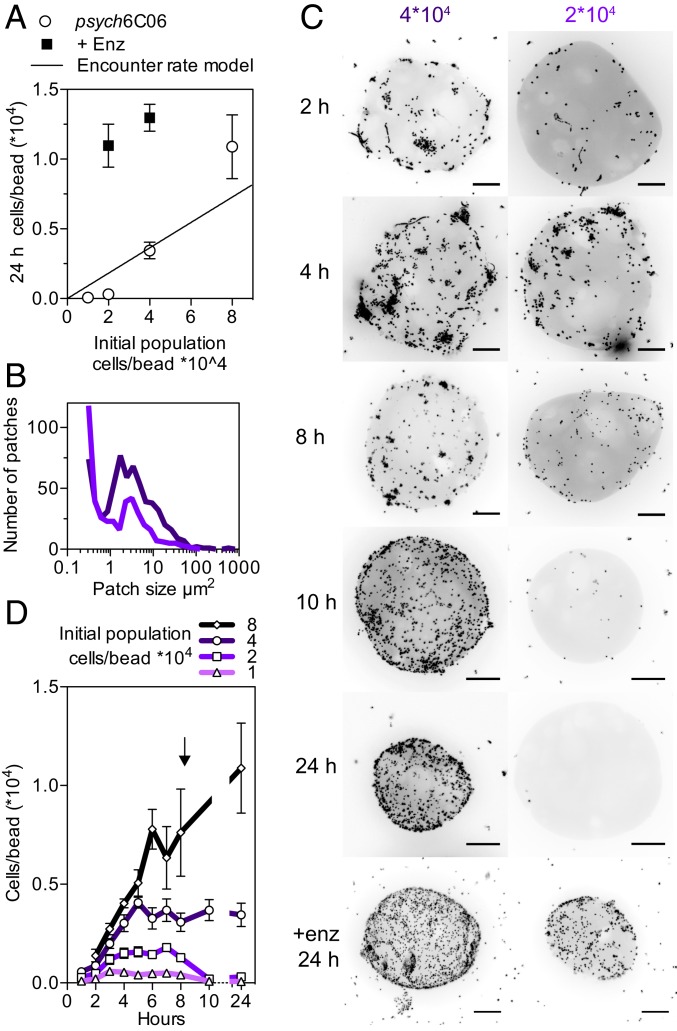
To experimentally validate our prediction that cell–cell cooperation drives the degradation of hard-to-degrade polysaccharides, we turned our attention to Psychromonas sp., psych6C06, a marine isolate that had previously been enriched from coastal seawater on model chitin particles (10). The strain readily degrades chitin hydrogel with a half-life of ∼30 h (20) and encodes at least 8 predicted chitinases, or glycosyl hydrolase family 18 and 19 homologs, but no other families of glycosyl hydrolases, leading us to conclude that the strain is representative of a chitin specialist. We reasoned that if cooperative growth kinetics played a role in this system, we would observe a strong dependency between the initial number of cells that colonized the particle and the growth of the population. In particular, we would expect a critical cell density below which the population was unable to form the patches required to degrade particles, revealing that the degradation process was bacteria-limited.

In agreement with this prediction, psych6C06 displayed a strong density dependence when growing on hydrogel chitin particles in the form of a critical cell density below which the particles were not persistently colonized (Fig. 4A). At concentrations just below the threshold critical cell density, we observed the formation of fewer and smaller patches than at higher densities (Fig. 4B), and by 8 h, the initial population began to die off (Fig. 4A and SI Appendix, Fig. S10A), meaning that the population was not able to sustain the cell numbers needed to colonize particles or to degrade them (Fig. 4 C and D). At the colonization threshold, cells were able to maintain their initial population size, but not to support net growth (Fig. 4A). The colonization density of the particles at the critical threshold matched the population size predicted by measured rates of psych6C06 surface attachment and detachment (Fig. 4A and SI Appendix, Fig. S10 B and C), suggesting that a viable population must be maintained off the particle, in addition to on its surface. To test whether low particle lability limited the persistence of the population, we artificially increased K_p by adding exogenous chitinase to supply 776 µg/h GlcNAc, equivalent to the amount of chitinase produced by 7 × 10⁴ cells per particle psych6C06. Consistent with individual-based model results (Fig. 3D), the addition of the exogenous chitinase activity lowered the cell density-dependent threshold for colonization of the chitin particles (Fig. 4A), allowing the population to persist and grow on the particle (Fig. 4C). Taken together, our results show that oligosaccharide limitation leads to the emergence of cooperative growth behaviors.

Fig. 4.

Chitinase limitation and encounter rate drive critical population-density thresholds of chitin-degrading strain psych6C06. (A) Colonization of chitin particles by psych6C06 shows dependence on initial population density (open symbols) and chitinase production (closed symbols). Solid line gives the predicted colonization density based on measured surface residence time, without division or death. Above a critical threshold (intercept of encounter rate model and experimental data), populations are able to survive at their initial density or grow. Below this threshold (gray shaded zone), populations are unable to maintain their initial density, and they go extinct. Adding exogenous chitinase (776 GlcNAc µg per hour, filled circles) allows populations below the critical density to maintain their size and grow. In comparison, the K_p of psych6C06 chitinase is 13.5 g GlcNAc/g cells/h, meaning that the exogenous chitinase supplies the equivalent of 7 × 10⁴ cells/particle. (B) Distribution of psych6C06 cells in patches after 4 h. Dark purple line indicates an initial population of 4 × 10⁴ and light purple line indicates an initial population of 2 × 10⁴. (C) Representative images showing density-dependent colonization dynamics for initial populations of cells below (2 × 10⁴ cells/particle) and above (4 × 10⁴ cells/particle) the colonization threshold at times during colonization. +enz 24 h indicates the addition of exogenous chitinase, as earlier. (Scale bars, 20 µm.) (D) Particle colonization dynamics for populations of psych6C06 over the course of 24 h. Arrow indicates 8-h time, where populations below the critical threshold begin to decrease in density on chitin particles. Data points are combined from 3 experimental replicates. Initial population densities (cells/particle) are noted by symbols: diamonds, 8 × 10⁴; circles, 4 × 10⁴; squares, 2 × 10⁴; diamonds, 1 × 10⁴. Error bars are SEM from at least 6 individual measurements of colonization density on chitin particles from 3 independent experiments (at least 18 measurements). Lines represent the mean trajectory for each cell density.

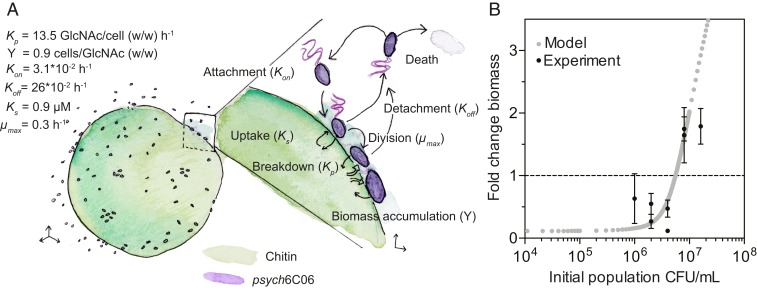
Finally, we tested whether the population-density-dependent threshold for cell–cell cooperation can be quantitatively predicted from cell physiology. We calculated the particle attachment and detachment rates by quantifying cell density on particles (Fig. 5A and SI Appendix, Fig. S10 B and C). Our measurements revealed rapid attachment and detachment rates (attachment rate, 0.03 h⁻¹; detachment rate, 0.26 h⁻¹; or equivalently a 3.8-h residence time). These rates were similar to those previously observed for natural marine bacterioplankton isolates (24) and were dependent on the density of cells off and on the particle, suggesting that psych6C06 populations undergo frequent exchange and rearrangement, similar to what we observed in our simulations (Fig. 3A). We measured K_p for psych6C06, using the fluorescent substrate 4-methylumbelliferyl-N-acetyl-β-d-glucosaminide, which detects the release of GlcNAc from chitin. We noted that very little chitinase activity was detected in the culture supernatant of psych6C06, but robust activity was associated with the cells themselves (Fig. 5A and SI Appendix, Fig. S10D), indicating that enzymes were membrane bound. Using methylumbelliferyl-conjugated substrates with different cleavage specificities, we determined that most of the psych6C06 chitinase activity was derived from exochitinase, which releases GlcNAc as a product (Fig. 5A and SI Appendix, Fig. S10E). Thus, we assessed the GlcNAc to biomass conversion factor (the biomass yield) of this strain by direct measurement of sugar consumption and cell density in exponentially growing cultures (Fig. 5A and SI Appendix, Fig. S10F). We measured the growth rate of psych6C06 on a range of GlcNAc concentrations, and used these substrate-limited growth measurements to derive µmax and K_s from a fit of the Monod growth equation (26) (Fig. 5A and SI Appendix, Fig. S10G). We parameterized a simplified version of the model with these measurements to describe population-level growth dynamics on a surface where cells can attach, detach, and grow as a function of the hydrolyzed product concentration (see Methods for a full description of the population-level model). This model assumes a rate of diffusive loss of oligosaccharides predicted from the individual-based simulations, and also that all cells on the surface experience the same environment (no local gradients). Using this simplified model, with no free parameters, we studied how the initial cell density determines the population-average colonization rate and the growth of bacteria on the particle surface. We found a remarkable quantitative agreement between this population-level model and our experiments, with critical thresholds predicted between initial densities of 2.5 × 10⁴ and 5 × 10⁴ cells/particle (Fig. 5B). Our analysis thus shows that cell-level physiology and behavior together with diffusion regulate the onset of social degradation of POM.

Fig. 5.

Physiological traits predict the population-density dependence of growth on chitin particles by psych6C06 in a diffusive environment. (A) Summary of measurements made to parameterize the population-level bottom-up model of psych6C06 growth on chitin. The key parameter for each process is given in parentheses: K_on, rate of cell attachment to particles (SI Appendix, Fig. S10B); K_off, rate of cell detachment from particles (SI Appendix, Fig. S10C); K_p, rate of GlcNAc release by cell-associated chitinase (SI Appendix, Fig. S10D); Y, the yield of GlcNAc conversion to biomass during carbon-limited growth (SI Appendix, Fig. S10F); K_s, Monod half-saturation constant for GlcNAc (SI Appendix, Fig. S10G); µ_max, maximum growth rate on GlcNAc (SI Appendix, Fig. S10G). wt/wt, ratio of weights. (B) Prediction of the fold change in biomass of psych6C06 populations after 24 h of growth on a chitin surface with an analytical model based on psych6C06 physiological the parameters measured in SI Appendix, Fig. S10 (gray points). Black data points show the experimentally measured change in biomass from Fig. 3A. Dotted horizontal line indicates no biomass change. Error bars represent SEM from at least 3 measurements of particle colonization density.

Discussion

Here we have shown that cell–cell cooperation, an emergent social behavior of populations, changes the rate and efficiency with which POM is broken down in aquatic environments. Cooperation emerged in populations as a result of 3 key physiological parameters: the affinity of cells for hydrolyzed oligosaccharide, the rate of polysaccharide hydrolysis, and the attachment and detachment of cells on/off the particle surface. These 3 parameters defined how public goods were shared among individuals in the population. Low hydrolysis rates favored cooperation because cell–cell clustering increased the uptake efficiency of soluble oligosaccharides. In contrast, when hydrolysis rates were high or when aggregates exceeded a certain size threshold, cell–cell clustering decreased the per capita access to resources, and instead promoted competition among cells. Remarkably, we observed that active rearrangement of cells caused the dissolution of cell clusters and mitigated competition, but decreased the per capita uptake efficiency. This observation also highlights the fact that in systems with potential for spatial self-organization, that is, most systems outside the laboratory, the balance between cooperation and competition can be delicate and is modulated by the intersection of physical processes with microbial physiology. Although our simulations reveal that physiology and diffusion alone are sufficient to explain the onset of cooperation, many bacteria actively regulate enzyme secretion and other group behaviors at the level of transcription in a density-dependent manner (32–35), potentially amplifying the effects described here.

Our study highlights 2 important consequences of bacteria–particle interactions in the ocean: most of the POM is lost to diffusion after hydrolysis, effectively turning into DOM, and density dependencies can control the degradation of recalcitrant polysaccharides. In simulations of an open, 3D environment, a faster depolymerization rate for labile particles meant that cells experienced higher local concentrations of oligosaccharide. However, a larger fraction of this oligosaccharide was lost to diffusion, thus reducing the final biomass yield of the population. Uptake efficiency was maximized on hard-to-degrade recalcitrant particles, where cell–cell cooperation was required to secure access to enough resources to maintain the population size and grow. As a consequence, we observed the emergence of cell density thresholds associated with the onset of cooperation, which drastically changed the hydrolysis rate of particles. This result contrasts with the assumption that the breakdown of POM in the environment is primarily controlled by abiotic factors, and that bacteria degrade it at fixed per capita rates (36–40). Instead, we showed experimentally that degradation in an environment such as the ocean can be bacteria-limited. Compared with the complexity of POM breakdown by polysaccharide-degrading microbes in the ocean, the model developed in this study is vastly simplified. However, such an approach presents an opportunity to address the fundamental question of how cellular and population-level microbial processes affect the turnover of organic matter in the ocean (41), and in particular, at what spatial and temporal scales variation impacts the higher-order function of communities or ecosystems (42).

Methods

Individual-Based Model of Cell Behavior and Physiology.

The mathematical model represents metabolism, surface interaction, and flagellar motility of individual cells in 3D space in the presence of chemical gradients. We introduce an individual-based model (43, 44) to quantify single-cell interactions with organic particles by abstracting the structural heterogeneities of natural POM into a mathematically simpler spherical shape, while preserving some key physical and chemical processes associated with POM degradation. A spherical organic particle of 200 µm radius is simulated such that it remains static in the middle of an aqueous volume (∼1 mm³). Although natural organic matter aggregates may show various shapes and chemical compositions, we modeled particles as perfect spheres made of a single type of insoluble linear polysaccharides such as chitin, alginate, or cellulose. This computational model is inspired by experimental model systems used to study community assembly on marine POM (10, 20). The particle’s size and its surface chemistry are assumed to be unchanged during particle degradation: only the particle density changes over time to satisfy mass conservation. This assumption is consistent with experimental observations that have shown no significant change in organic particle size during microbial degradation until the final stages of collapse (20). We simulated a scenario in which an isogenic population of cells is allowed to colonize and degrade a particle with a defined volume. The simulations were started with zero oligosaccharides, and the particle was considered to be the sole carbon source.

To take into account the fact that cells might regulate their enzymatic activity, the model limits enzyme secretion to 2 scenarios: when cells adhere to the particle surface or when the rate of oligosaccharide supply exceeds the maintenance threshold. Importantly, our simulations ensure mass conservation between total carbon uptake and growth and loss of oligosaccharides. Individual cells are initialized as a uniform random distribution in the aqueous volume, and are allowed to disperse following gradients of chemoattractant (in this case, oligosaccharide). The cells can consume the oligosaccharide, grow, and divide to new daughter cells and experience a range of local conditions. A full derivation of the mathematical expressions and steps used for modeling of microbial growth, dispersal, and enzyme secretion can be found in the SI Appendix.

Experimental Methods.

Strain psych6C06 was previously isolated from an enrichment of nearshore coastal seawater (Nahant, MA) for surface-associated chitin degrading microbial communities (10, 20). The strain was maintained as colonies on Marine Broth 2216 (Difco 279110) with 1.5% agar (BD 214010). To establish exponential growth, we modified a culturing protocol previously developed for Escherichia coli K12 (45) and grew cells on a defined seawater medium with the N-acetyl-_D-glucosamine (GlcNAc) at the concentrations indicated. Chitin hydrogel particles (NEB) were washed and diluted to 200 to 250 particles per milliliter with size range from 40 to 100 μm in diameter. The particles were rotated end over end at 21 °C to 25 °C. The density of inoculated cells was set to be at an absorbance at 600 nm, (A₆₀₀) of 0.01, diluted from 20 mM GlcNAc minimal medium cultures prepared as described earlier. To visualize particles and their surface-associated bacteria, 200-µL subsamples were stained with the DNA-intercalating dye SYTO9 (Thermo Fisher, S34854) at a 1:285 dilution of the stock in 96-well plates with optically clear plastic bottoms (VWR 10062-900).

Cell density measurements A₆₀₀ of exponentially growing cells were used to measure the maximum cellular growth rate, and plating was used to measure growth under GlcNAc limitation, from which we derived the half-saturation constant. GlcNAc depletion was measured during growth, using the dintrosalicylic acid reagent method (46), and the depletion rate was used to calculate the biomass yield (SI Appendix).

Chitinase activity was quantified using methylumbelliferyl-conjugated substrates N,N′-diacetyl-β-d-chitobioside, N-acetyl-β-d-glucosaminide, and β-d-N,N′,N′′-triacetylchitotriose (Sigma CS1030). Microscopy was performed on microconfocal high-content imaging system (ImageXpress Micro Confocal, Molecular Devices), using the 60-µm pinhole spinning disk mode. Fluorescent signal was visualized with a LED light cube (Lumencore Spectra X light engine), and bandpass filters (ex 482/35 nm em 538/40 nm dichroic 506 nm), with a 40× objective (Nikon Ph 2 S Plan Fluor ELWD ADM 0.60 NA cc 0 to 2 mm, correction collar set to 1.1), and a sCMOS detector (Andor Zyla). Image analysis was performed in MATLAB (release 2018a). Briefly, image stacks were split in half and a maximum intensity projection was obtained for each half. The low level of fluorescent signal associated with free dye in the hydrogel particles was used to define an intensity threshold suitable to create a binary mask for the particle projections. A mask of the cells on the particles was then defined using their brighter fluorescence intensity. We used this segmentation to quantify the total surface area occupied by the cells on the particle and to quantify the total surface area occupied by patches. We define patches as an area greater than that equivalent to 3 cells (>10 µm²), where cells contact other cells or were in close proximity (<10 µm from nearest neighbor). This definition is analogous to the spacing constraints defined in the individual-based simulation.