Modeling the inhibition of breast cancer growth by GM-CSF

Abstract

M-CSF is overexpressed in breast cancer and is known to stimulate macrophages to produce VEGF resulting in angiogenesis. It has recently been shown that the growth factor GM-CSF injected into murine breast tumors slowed tumor growth by secreting soluble VEGF receptor-1 (sVEGFR-1) that binds and inactivates VEGF. This study presents a mathematical model that includes all the components above, as well as MCP-1, tumor cells, and oxygen. The model simulations are representative of the in vivo data through predictions of tumor growth using different protocol strategies for GM-CSF for the purpose of predicting higher degrees of treatment success. For example, our model predicts that once a week dosing of GM-CSF would be less effective than daily, twice a week, or three times a week treatment because of the presence of essential factors required for the anti-tumor effect of GM-CSF.

1. Introduction

Macrophages play an essential role in normal breast development, especially during pregnancy and lactation (Pollard, 1997), but also during the development and progression of breast tumors. It has been reported that the macrophage survival and differentiation factor, macrophage colony-stimulating factor (M-CSF), are overexpressed in over 70% of human breast cancers (Sapi, 2004). Correspondingly, mice deficient in M-CSF is protected against breast tumor metastasis while overexpression of M-CSF in these same mice recovered tumor metastasis to the lung (Lin et al., 2001).

It was shown by Eubank et al. (2003) that M-CSF induces monocytes and macrophages to produce biologically-active vascular endothelial growth factor (VEGF), thereby mobilizing endothelial cells and inducing angiogenesis. In breast tumors, these tumor-associated macrophages (TAMs) constitute up to 35% of infiltrating inflammatory cells (Tang et al., 1992) and reside mostly in hypoxic regions of the tumor core—clearing dead cell debris. TAMs are recruited into the tumors by monocyte chemoattractant protein-1 (MCP-1) which is released from both stromal cells and tumor cells (Fujimoto et al., 2009). Interestingly, depending on their polarity, either M1- or M2-type macrophages can play two different roles in the regulation of tumor growth. On the one hand, M1 macrophages produce high levels of interleukins IL-12, IL-23, IL-1, IL-6, TNFa, the chemokine CXCL10, inducible nitric oxide synthase (iNOS), human leukocyte antigen (HLA)-DR, reactive oxygen and nitrogen that help fight tumor growth (Mantovani et al., 2007, 2005; Baj-Krzyworzeka et al., 2007; Mantovani et al., 2002). On the other hand, M2 macrophages express high levels of IL-10, IL-ra, CCL22, scavenger, mannose and galactose receptors, arginase I, CD163 antigen, matrix metalloproteinases (MMPs), and VEGF which serve to help tumor progression (Mantovani et al., 2007; Gordon, 2003; Hagemann et al., 2004).

In a follow-up to their report showing that the growth factor granulocyte/macrophage colony-stimulating factor (GM-CSF) induces monocytes to secrete soluble VEGF receptor-1 (sVEGFR-1) which binds to and inactivates VEGF (Eubank et al., 2004), Eubank et al. (2008) investigated the hypothesis that macrophage phenotype and behavior in breast tumors can be manipulated in vivo by GM-CSF. It was previously known that GM-CSF can enhance the ability of macrophages to present antigen and initiate an immune response (Armstrong et al., 1996). In the study (Eubank et al., 2008), MET-1 mammary tumor cells were orthotopically-injected into normal female FVB/N mice. After tumors became palpable (approximately 28 days after seeding), 100 ng GM-CSF was injected directly into the tumors three times a week. Treatment with GM-CSF reduced tumor growth and metastasis; moreover, GM-CSF lowered oxygen tension and reduced blood vessel density within the tumor by suppressing angiogenic activity. Further, Eubank et al. (2008) showed that tumors treated with GM-CSF had more TAMs of an M1 polarity while vehicle-treated tumors had more M2-type and support the role of GM-CSF contributing to an M1 phenotype (Mantovani et al., 2007). The experimental data also demonstrated that GM-CSF reversed some of the pro-tumor “education” of immune cells driven by tumor cell:macrophage interaction and induced a more anti-tumor phenotype from the TAMs.

There have been a number of mathematical studies modeling the macrophage infiltration into avascular tumors (Owen and Sherratt, 1997; Kelly et al., 2002; Owen et al., 2004), i.e., a tumor small enough to be able to satisfy its nutritional needs by diffusion from nearby blood vessels. These studies focused either on the possibility of spatial pattern formation within the growing tumor (Owen and Sherratt, 1997), or on the dependence of the macrophage infiltration pattern on the motility mechanisms (random motion, chemotaxis) (Armstrong et al., 1996). Macrophage chemotactic sensitivity has been shown to be a key determinant of macrophage infiltration and tumor size (Kelly et al., 2002; Owen et al., 2004). Increased infiltration should be beneficial in the context of macrophage-based therapies; however, such infiltration in fact leads to increased tumor size (Kelly et al., 2002).

In the present study, we develop a mathematical model to predict the effect of GM-CSF treatment on tumor growth in a mouse model of breast cancer. The model takes into account the experimentally established interactions among cancer cells, macrophages, free endothelial cells, MCP-1, VEGF and M-CSF. Simulations of the model predict the effect of GM-CSF treatment on slowing tumor growth, and these predictions fit reasonably well with the in vivo experimental data of Eubank et al. (2008). Our hope is to incorporate modeling methods such as this to predict treatment success on various existing strategies in the clinical setting in terms of both the dosage and frequency of treatment. In fact, methods are currently being investigated to obtain more detailed information from the tumor microenvironment like tumor pH, intracellular glutathione, and redox potential that may affect existing chemotherapy drugs. Using these new data, better simulations could be generated for use in patients with breast cancer.

2. The model

We shall represent blood vessels in terms of the endothelial cells (EC) which line the interior of the capillaries. For simplicity we take the tumor to be a sphere and we denote its radius at time t by R(t). The tumor region is defined by 0 ≤ r ≤ R(t) and the model’s variables are given in Table 1.

Table 1.

Model variables.

c	Live tumor cell density (cell cm−3)
b	Dead tumor cell density (cell cm−3)
w	Oxygen density (g cm−3)
e	Endothelial cell density (cell cm−3)
h	VEGF density (g cm−3)
s	M-CSF density (g cm−3)
m	Macrophage density (cell cm−3)
p	MCP-1 density (g cm−3)
g	GM-CSF density (g cm−3)

We assume that these variables are radially symmetric, i.e., they depend only on r and t. It is also assumed that the macrophage density depends on the GM-CSF administration, in fact, GM-CSF induces macrophage chemotaxis (Ribatti et al., 2007).

The evolution of tumor cell density is given by

$$\frac{\partial c}{\partial t}=D_c\mathrm{\Delta }c+\underset{\text{necrosis }}{\underbrace{{\lambda }_0(w)c}}+\underset{\text{proliferation }}{\underbrace{{\lambda }_1(w)c\left(1-\frac{c+m+\delta b}{c^{*}}\right)}}-\underset{\text{apoptosis }}{\underbrace{{\mu }_{c}C}}.$$ (1)

The constant c* represents the total capacity of tumor cells (live and dead) and macrophages competing for space, δ, are chosen such that 0 < δ < 1, since the volume of dead cells is smaller than the volume of live cells (Ward and King, 1997). The first term on the right-hand side accounts for the diffusion of tumor cells, the second term represents the fact that cells die at low oxygen concentrations at rate λ₀(w) by necrosis, and the last term accounts for death due to apoptosis. Tumor cells are assumed to undergo a logistic growth and compete for space with macrophages and dead cells. The function λ₁(w) is the growth rate of tumor cells. We assume that for oxygen concentration w in some range w_n < w < w₁ cells are in quiescent phase; and for w > w₁, the growth rate λ₁(w) increases linearly in w, until it reaches a constant level when w crosses the hypoxic level w_h. The range w₁ < w < w_h is considered to be in the hypoxic (but not extreme hypoxic) range, whereas the range w > w₁ is viewed as the normoxic range; one does not expect to have hyperoxic conditions within the tumor. Following (Breward et al., 2001), we choose w₁ = 1.6w_n. Hence

$${\lambda }_1(w)=\{\begin{array}{ll}0\hfill & \text{ if }{w}_n\le w\le w_1,\hfill \\ \frac{{\lambda }_1}{w_h-w_n}\left(w-w_1\right)\hfill & \text{ if }{w}_1<w\le w_h,\hfill \\ {\lambda }_1\hfill & \text{ if }w>w_h.\hfill \end{array}$$ (2)

The rate of necrosis is assumed to occur at a faster rate than proliferation (Breward et al., 2001), and we take

$${\lambda }_0(w)=-2{\lambda }_1\frac{w_n-w}{w_n}\text{ if }w<w_n.$$ (3)

The evolution of dead tumor cell density is given by

$$\frac{\partial b}{\partial t}=D_b\mathrm{\Delta }b\underset{\text{gain from live tumor cells }}{\underbrace{-{\lambda }_0(w)c+{\mu }_{c}c}}-\underset{\text{clearance }}{\underbrace{{\mu }_b\frac{w}{w_0}mb}},$$ (4)

where w₀ is the oxygen density in normal tissue. The first term on the right-hand represents the dispersion of dead cells. The second and third terms account for the gain of dead cells due to death of tumor cells. Clearance of dead cells is driven by macrophages whose efficiency increases as the oxygen level increases.

The oxygen density evolves according to

$$\frac{\partial W}{\partial t}=D_w\mathrm{\Delta }w+\underset{{\text{O}}_2\text{ delivered by EC }}{\underbrace{{\lambda }_{2}e}}-\underset{\text{uptake by macrophages }}{\underbrace{{\lambda }_{3}wm}}-\underset{\text{uptake by tumor }}{\underbrace{{\lambda }_{4}wC}}.$$ (5)

The first term in Eq. (5) accounts for the diffusion of oxygen and the second term accounts for the oxygen diffused from the vasculature. Oxygen is being taken up by both macrophages and tumor cells.

We view the vascular system as being represented by the density of the endothelial cells. The evolution of the endothelial cell density is given by

$$\frac{\partial e}{\partial t}=D_e\mathrm{\Delta }e-\underset{\text{chemotaxis }}{\underbrace{\nabla \cdot \left({\kappa }_{h}e\nabla h\right)}}+\underset{\text{proliferation }}{\underbrace{{\lambda }_{5}e\left(1-\frac{e}{e_1}\right)\left(\frac{h-h_1}{h_0}\right)H\left(h-h_1\right)}},$$ (6)

where e₁ is the maximal EC density inside the tumor and it will be estimated later. The second term in the right-hand side of Eq. (6) accounts for the VEGF-dependent chemotactic movement of endothelial cells; we assume that the chemotactic coefficient κ_h is constant. Endothelial cells undergo a logistic type growth which is controlled by VEGF, and this is reflected by the third term in the right-hand side of Eq. (6). We assume that without the influence of VEGF, endothelial cells proliferation and apoptosis balance each other, so that net proliferation is due primarily to VEGF influence. We also assume that there is a threshold concentration level of VEGF below which proliferation does not occur (Acker et al., 2001; Seghezzi et al., 1998). This is expressed by the term H(h−h₁), where H(·) is the Heaviside function. A similar term λ₅e(1−(e/e₀))((h−h₁)/h₀)H(h−h₁) was introduced in (Chaplain, 1995, p. 390 where e₀ accounts for the EC density in normal tissue; in our case, e₁ is the maximal EC density inside the tumor.

The density of the chemoattractant VEGF evolves according to

$$\frac{\partial h}{\partial t}=D_h\mathrm{\Delta }h+\underset{\text{secretion by tumor and macrophages }}{\underbrace{{\lambda }_6(w)c+{\lambda }_7(w)\frac{s}{m+m_c}m}}-\underset{\text{GM-CSF inhilition }}{\underbrace{{\lambda }_{8}gmh}}-\underset{\text{decay }}{\underbrace{{\mu }_{h}h}}.$$ (7)

The first and last terms in Eq. (7) account for diffusion and decay of VEGF. The second and third terms on the right-hand side account for the fact that VEGF is produced by both the tumor cells and macrophages triggered by M-CSF. The c-macrophage receptor that activates the signal transduction pathway which leads to VEGF (and MCP-1) expression in macrophages is responsible for the saturation effect in both VEGF and MCP-1 production by macrophages (Varney et al., 2005; Leonard et al., 1991; Curry et al., 2008; Eubank et al., 2003). The oxygen-dependent rates λ₆(w) and λ₇(w) are chosen as follow:

$${\lambda }_6(w)=\{\begin{array}{ll}0\hfill & \text{ if }w<w_n,\hfill \\ \frac{4{\lambda }_6}{w_1-w_n}\left(w-w_n\right)\hfill & \text{ if }{w}_n\le w\le w_1,\hfill \\ 4{\lambda }_6\hfill & \text{ if }{w}_1<w\le w_h,\hfill \\ {\lambda }_6\hfill & \text{ if }w>w_h\hfill \end{array}$$ (8)

and

$${\lambda }_7(w)=\{\begin{array}{ll}0\hfill & \text{ if }w<w_n,\hfill \\ \frac{2{\lambda }_7}{w_1-w_n}\left(w-w_n\right)\hfill & \text{ if }{w}_n\le w\le w_1,\hfill \\ 2{\lambda }_7\hfill & \text{ if }{w}_1<w\le w_h,\hfill \\ {\lambda }_7\hfill & \text{ if }w>w_h\hfill \end{array}.$$ (9)

Based on Lewis and Murdoch (2005), it is assumed here that VEGF production takes place only when w is above the necrotic level w_n, that this production rate increases with w, but falls off when w arises above the hypoxic level; more details are given in Section 2.8. The third term on the right-hand side of Eq. (7) accounts for the fact that GM-CSF stimulates macrophages to secrete soluble VEGF receptor which combines with VEGF and neutralizes it (Eubank et al., 2003).

M-CSF evolves according to

$$\frac{\partial S}{\partial t}=D_s\mathrm{\Delta }s+\underset{\text{secretion by tumor }}{\underbrace{{\lambda }_{9}C}}-\underset{\text{decay }}{\underbrace{{\mu }_{s}S}},$$ (10)

where the first and last terms account for diffusion and decay, and the middle term accounts for the fact that M-CSF is produced by tumor cells (Leitzel et al., 2007). The parameter λ₉ is independent of the oxygen levels since the M-CSF promoter does not have HRE (hypoxia regulatory element), which senses low oxygen and responds by producing higher levels of the gene (Oren et al., 2001).

The equation for the macrophage density is

$$\frac{\partial m}{\partial t}=D_m\mathrm{\Delta }m-\underset{\text{chemotaxis by MCP-}1}{\underbrace{\nabla \cdot \left({\kappa }_{p}m\nabla p\right)}}-\underset{\text{chemotaxis by GM-CSF }}{\underbrace{\nabla \cdot \left({\kappa }_{g}m\nabla g\right)}}.$$ (11)

The second and third terms account for their recruitment in response to chemoattractants MCP-1 and GM-CSF (Owen et al., 2004; DeVita et al., 2008, p. 2622). The chemotactic coefficients κ_p and κ_g are assumed to be constants.

MCP-1 is predominantly produced by macrophages and is a potent chemotactic factor for monocytes (Kanda et al., 2006). MCP-1 is produced in response to M-CSF binding the M-CSF receptor (Varney et al., 2005; Leonard et al., 1991; Curry et al., 2008; Eubank et al., 2003), a process that results in saturation due to limited M-CSF receptors. Hence, the MCP-1 equation is

$$\frac{\partial p}{\partial t}=D_p\mathrm{\Delta }p+\underset{\text{secretion by macrophages }}{\underbrace{{\lambda }_{10}(w)\frac{s}{m+m_c}m}}-\underset{\text{decay }}{\underbrace{{\mu }_{p}p}}.$$ (12)

Hypoxia inhibits the production of MCP-1 from macrophages; the extent of inhibition ranging from 2.3- to 2.8-fold compared to normoxia (Bosco et al., 2004). Hence, we take

$${\lambda }_{10}(w)=\{\begin{array}{ll}0\hfill & \text{ if }w<w_n,\hfill \\ \frac{2}{5}{\lambda }_{10}\hfill & \text{ if }{w}_n\le w\le w_h,\hfill \\ {\lambda }_{10}\hfill & \text{ if }w>w_h.\hfill \end{array}$$ (13)

The GM-CSF equation is

$$\frac{\partial g}{\partial t}=D_g\mathrm{\Delta }g+\underset{\text{injection }}{\underbrace{f(t)}}-\underset{\text{decay }}{\underbrace{{\mu }_{g}g}},$$ (14)

where the second term f(t) accounts for injecting GM-CSF periodically, depending on the dosing regimen.

2.1. Boundary conditions

Since the variables are radially symmetric, they all satisfy a no-flux condition at r = 0,t > 0. We assume that on the tumor boundary r = R(t) the live tumor cell density is constant and that there are no dead cells. This assumption is justified since on the tumor boundary cells have a good supply of oxygen, so they do not undergo necrosis. All other variables (macrophages, EC, cytokines, oxygen) satisfy a Robin-type boundary condition

$$\begin{gathered} C{|}_{r=R(t)}=c_0,b{|}_{r=R(t)}=0, \\ \frac{\partial e}{\partial r}+{\gamma }_1\Phi (h)\left(e-e_0\right){|}_{r=R(t)}=0,\frac{\partial m}{\partial r}+{\gamma }_1\Gamma (p,g)\left(m-m_1\right){|}_{r=R(t)}=0, \\ \Psi (e)\frac{\partial w}{\partial r}+{\gamma }_1\left(w-w_0\right){|}_{r=R(t)}=0, \\ \frac{\partial s}{\partial r}+{\gamma }_{2}s{|}_{r=R(t)}=0,\frac{\partial p}{\partial r}+{\gamma }_{2}p{|}_{r=R(t)}=0,\frac{\partial h}{\partial r}+{\gamma }_{2}h{|}_{r=R(t)}=0, \\ \frac{\partial g}{\partial r}+{\gamma }_{2}g{|}_{r=R(t)}=0. \end{gathered}$$

Here m₁ is the average macrophage density for the untreated tumor, as measured in Eubank et al. (2008), γ₁ Φ(h) is the relative flux (∂e/∂r)/(e₀–e) of EC (similarly for macrophages and oxygen), γ₂ is the relative flux of the cytokines (s,p,h,g), and

$$\Phi (h)=\frac{h}{h+{\alpha }_1},\Gamma (p,g)=\frac{p}{p+{\alpha }_2}+\frac{g}{g+{\alpha }_3},\Psi (e)=\frac{{\alpha }_4}{e+{\alpha }_5},$$

where α_i, i = 1,. ., 5 are positive parameters. The form of the functions Φ(h),Γ(p,g),Ψ(e) represents the fact that the relative flux of EC, macrophages and oxygen increases with VEGF, MCP-1 and GM-CSF, and EC, respectively. Although we have assumed here a specific form for Φ(h),Γ(p,g),Ψ(e), the simulation results of our model do not significantly change if the form of these functions is not significantly altered.

2.2. Initial conditions

Palpable tumors had volume 1–2 mm³ in Eubank et al. (2008). We take initial volume of 1 mm³, which corresponds to initial radius R₀ = 0.6 mm. We also take the initial values

$$\begin{gathered} c(r,0)=c_0,b(r,0)=0,w(r,0)=w_0,e(r,0)=0, \\ m(r,0)=m_1{e}^{-\left(R_0-x\right)/ϵ}, \\ h(r,0)=0,s(r,0)=0,p(r,0)=0,g(r,0)=0\left(0<r<R_0\right), \end{gathered}$$

where ϵ > 0.

2.3. Interface condition

We assume that live tumor and macrophage cells have the same volume, which is typically V_L = 10⁻⁹ cm³ (Ward and King, 1997). Cells that just died have the same volume as live cells, but shortly after they are degraded. Thus, on the average we view each volume of a dead cell as being a fraction of the volume of a live cell; we take it to be δV_L, where δ = 0.3. Hence, the total volume occupied by the cells is

$$\left[{\int }_{r<R(t)}(m(r,t)+c(r,t)+\delta b(r,t))\right]\times {10}^{-9}{\text{ cell cm}}^{-3}.$$

Since the cells occupy only a fraction θ of the total volume V(t) of the tumor, where θ is a constant to be determined later on

$$\rho \theta V(t)={\int }_{r<R(t)}(m(r,t)+c(r,t)+\delta b(r,t))\text{ and }\rho ={10}^9{\text{ cell cm}}^{-3}.$$

In order to determine how the tumor boundary r = R(t) varies in time we differentiate the last equation with respect to t and use the boundary conditions for c and b

$$\rho \theta \frac{dV}{dt}=\frac{d}{dt}{\int }_{r<R(t)}(m(r,t)+c(r,t)+\delta b(r,t))=\left(m(R(t),t)+c_0\right)\frac{dV}{dt}+{\int }_{r<R(t)}\frac{\partial }{\partial t}(m(r,t)+c(r,t)+\delta b(r,t)).$$

The integral term can be written as

$${\int }_{r<R(t)}\frac{\partial }{\partial t}(m(r,t)+c(r,t)+\delta b(r,t))=\Theta (c,b,m,p,g)\left(4\pi R^2\right)+{\int }_{r<R(t)}\left({\lambda }_1(w)c\left(1-\frac{c+m+\delta b}{c^{*}}\right)-\delta {\mu }_b\frac{w}{w_0}mb\right),$$

where

$$\Theta (c,b,m,p,g)=-{\kappa }_{g}m(R(t),t)\frac{\partial g}{\partial r}(R(t),t)-{\kappa }_{p}m(R(t),t)\frac{\partial p}{\partial r}(R(t),t)+D_m\frac{\partial m}{\partial r}(R(t),t)+D_c\frac{\partial C}{\partial r}(R(t),t)+\delta D_b\frac{\partial b}{\partial r}(R(t),t).$$ (15)

It follows that

$$\frac{dV}{dt}\left(\rho \theta -m(R(t),t)-c_0\right)=\Theta (c,b,m,p,g)\left(4\pi R^2\right)+{\int }_{r<R(t)}\left({\lambda }_1(w)c\left(1-\frac{c+m+\delta b}{c^{*}}\right)-\delta {\mu }_b\frac{w}{w_0}mb\right),$$

or, after dividing by 4πR²

$$\frac{dR}{dt}=\frac{\Theta \left(c,b,m,p,g\right)}{\rho \theta -m\left(R\left(t\right),t\right)-c_0}+\frac{{\int }_0^{R\left(t\right)}\left(\lambda 1\left(w\right)c\left(1-\frac{c+m+\delta b}{c^{\ast }}\right)-\delta {\mu }_b\frac{w}{w_0}mb\right)r^{2}dr}{R^2\left(\rho \theta -m\left(R\left(t\right),t\right)-c_0\right)}.$$ (16)

2.4. Parameters

Table 2 lists the values of the parameters which appear in Eqs. (1)–(14) in dimensional and dimensionless forms. The last column gives reference to experimental data. When such data were not available, the parameters were estimated; some of these estimates are based on unpublished observations by co-authors Eubank and Roberts. The conversion from the dimensional to dimensionless units is done as follows:

$$\begin{gathered} \widehat{r}=\frac{r}{L},\widehat{t}=\frac{t}{\tau },\widehat{C}=\frac{C}{C_0},\widehat{b}=\frac{b}{c_0},\widehat{e}=\frac{e}{e_0},\widehat{m}=\frac{m}{m_0},{\widehat{C}}^{*}=\frac{c^{*}}{c_0}, \\ \widehat{w}=\frac{w}{w_0},\widehat{h}=\frac{h}{h_0},\widehat{s}=\frac{s}{s_0},\widehat{p}=\frac{p}{p_0},\widehat{g}=\frac{g}{g_0},{\widehat{m}}_c=\frac{m_c}{m_0}, \\ \left\{{\widehat{D}}_c,{\widehat{D}}_b,{\widehat{D}}_w,{\widehat{D}}_e,{\widehat{D}}_h,{\widehat{D}}_m,{\widehat{D}}_p,{\widehat{D}}_g\right\}=\left\{D_c,D_b,D_w,D_e,D_h,D_s,D_m,D_p,D_g\right\}\frac{\tau }{L^2}, \\ \left\{{\widehat{\lambda }}_0(w),{\widehat{\lambda }}_1(w),{\widehat{\lambda }}_2,{\widehat{\lambda }}_3,{\widehat{\lambda }}_4,{\widehat{\lambda }}_5\right\}=\tau \left\{{\lambda }_0(w),{\lambda }_1(w),\frac{e_0{\lambda }_2}{w_0},{\lambda }_3{m}_0,c_0{\lambda }_4,{\lambda }_5\right\} \\ \left\{{\widehat{\lambda }}_6(w),{\widehat{\lambda }}_7(w),{\widehat{\lambda }}_8,{\widehat{\lambda }}_9,{\widehat{\lambda }}_{10}(w)\right\}=\tau \left\{\frac{c_0}{h_0}{\lambda }_6(w),\frac{m_0}{h_0}{\lambda }_7(w),{\lambda }_8{g}_0{m}_0,\frac{c_0}{s_0}{\lambda }_9,\frac{m_0{\lambda }_{10}}{p_0}\right\}, \\ \left\{{\widehat{\kappa }}_h,{\widehat{\kappa }}_p,{\widehat{\kappa }}_g\right\}=\left\{{\kappa }_h{h}_0,{\kappa }_p{p}_0,{\kappa }_g{g}_0\right\}\frac{\tau }{L^2}, \\ \left\{{\widehat{\mu }}_c,{\widehat{\mu }}_b,{\widehat{\mu }}_h,{\widehat{\mu }}_s,{\widehat{\mu }}_m,{\widehat{\mu }}_p,{\widehat{\mu }}_g\right\}=\left\{{\mu }_c,m_0{\mu }_b,{\mu }_h,{\mu }_s,{\mu }_m,{\mu }_p,{\mu }_g\right\}\tau , \\ {\widehat{m}}_1=\frac{m_1}{m_0},{\widehat{\alpha }}_1=\frac{{\alpha }_1}{h_0},{\widehat{\alpha }}_2=\frac{{\alpha }_2}{p_0},{\widehat{\alpha }}_3=\frac{{\alpha }_3}{g_0},{\widehat{\alpha }}_{4,5}=\frac{{\alpha }_{4,5}}{e_0}, \\ {\widehat{\gamma }}_{1,2}={\gamma }_{1,2}L,\widehat{ϵ}=\frac{ϵ}{L}, \end{gathered}$$

where the scaling parameters L,τ,e₀,s₀,p₀,g₀ are given at the bottom of Table 2. We choose the length scale L = 0.5 cm and time scale τ = L²/max{D_c,D_b,D_w,D_e,D_h,D_s,D_m,D_p}; then τ = 0.5 cm²/10⁻⁶ cm² s⁻¹ = 2.9 days; this is comparable with the estimated tumor volume doubling time in Eubank et al. (2008), around 2.5 days.

Table 2.

Parameter values.

Parameter	Dimensional value	Dimensionless value	Reference
Dc	10−10 cm2 s−1	10−4	Owen et al. (2004), and estimated
Db	10−10 cm2 s−1	10−4	Estimated
Dm	5 × 10−11 cm2 s−1	5 × 10−5	Owen et al. (2004)
Dh	5 × 10−7 cm2 s−1	0.5	Schugart et al. (2008)
De	10−11 cm2 s−1	10−5	Owen et al. (2004), Plank et al. (2004), and estimated
Dw	5 × 10−7 cm2 s−1	0.5	Schugart et al. (2008), Owen et al. (2004)
Ds	10−6 cm2 s−1	1	Estimated
Dp	10−6 cm2 s−1	1	Owen et al. (2004), Owen and Sherratt (1997), and estimated
Dg	5 × 10−8 cm2 s−1	0.05	Caldwell et al. (1991), and estimated
λ1	10−5 s−1	2.53	Owen et al. (2004) and Qian et al. (2009)
λ2	7 × 10−16 g s−1 cell−1	0.93	Estimated
λ3	7 × 10−13 cm3 s−1 cell−1	35	Girgis-Gabardo and Hassell (2008)
λ4	4 × 10−13 cm3 s−1 cell−1	70	Butterworth and Cater (1967), Chen et al. (2009), and estimated
λ5	7 × 10−6 s−1	1.74	Chaplain et al. (1995), and estimated
λ6	2.12 × 10−22 g s−1 cell−1	3.72	Braunstein et al. (2007), Owen et al. (2004), Owen and Sherratt (1997), Pyaskovskaya et al. (2008), and estimated
λ7	1.48 × 10−21 g s−1 cell−1	7.43	Melillo et al. (1999), Vicioso et al. (2006), and estimated
λ8	4 × 105 cm3 g−1 s−1 cell−1	8 × 105	Estimated
λ9	3.18 × 10−22 g s−1 cell−1	5.57	Oren et al. (2001), Utting et al. (2010), and estimated
λ10	1.48 × 10−21 g s−1 cell−1	7.43	Bosco et al. (2004), and estimated
kh	1 cm5 g−1 s−1	0.01	Schugart et al. (2008)
kp	6 cm5 g−1 s−1	0.06	Owen et al. (2004)
kg	0.909 cm5 g−1 s−1	0.0091	Estimated
wh	1.07 × 10−4 g cm−3	0.23	Vaupel et al. (2003), and estimated
wn	3.35 × 10−5 g cm−3	0.072	Vaupel et al. (2003), and estimated
w0	4.65 × 10−4 g cm−3	1	Vaupel et al. (2003)
α1,h0	10−8 g cm−3	1	Schugart et al. (2008)
c0	7 × 108 cell cm−3	1	Vincensini et al. (2007) and Eubank et al. (2008)
m0	2 × 108 cell cm−3	1	Eubank et al. (2008)
c*	9.45 × 108 cell cm−3	1.35	Estimated
h1	3.65 × 10−10 g cm−3	0.036	Chaplain (1995), and estimated
m1,mc	108 cell cm−3	0.5	Eubank et al. (2008)
e1	5 × 106 cell cm−3	2	Estimated
μc	5 × 10−6 s−1	1.26	Breward et al. (2001)
μb	5 × 10−14 cm3 s−1 cell−1	2.53	Breward et al. (2001), and estimated
μh	1.26 × 10−4 s−1	31.6	Plank et al. (2004)
μs	4.8 × 10−5 s−1	12	Tang (2000)
μg	1.6 × 10−5 s−1	4	Williams et al. (1999)
μp	2 × 10−5 s−1	5	Owen and Sherratt (1997)
α2,3	10−10 g cm−3	0.01	Estimated
α4	2.5 × 105 cell cm−3	0.1	Estimated
α5	2.5 × 104 cell cm−3	0.01	Estimated
γ1	2 cm−1	1	Estimated
γ2	0.2 cm−1	0.1	Estimated
ϵ	0.05 cm	0.1	Estimated
e0	2.5 × 106 cell cm−3	1	Scaling parameter, Less et al. (1991), Levine and Nilsen-Hamilton (2006), Hashizume (2000)
τ	2.5 × 105 s	1	Scaling parameter, estimated
L	0.5 cm	1	Scaling parameter, estimated
s0,p0,g0	10−8 g cm−3	1	Scaling parameter, estimated

2.5. Hypoxic/necrotic and VEGF threshold

The mean oxygen pressure in breast tumor patients is in the range of 3–15 mm Hg, while in normal breast tissue the mean oxygen pressure is substantially higher (52 mm Hg) in Vaupel et al. (2003). Accordingly, we take:

• O₂ pressure in normal breast tissue is p₀=52 mm Hg,

• maximal O₂ pressure in hypoxic region of tumor is p_h = 12 mm Hg,

• maximal O₂ pressure in dead/necrotic region of tumor is p_n = 3.75 mm Hg.

The O₂ pressure in air is p_a = 160 mm Hg (Lane, 2002, p. 166). Since oxygen density is proportional to its pressure and O₂ density in air is ρ_a = 1.43 × 10⁻³ g cm⁻³ (Getman, 1908, p. 259), we obtain w₀ = (p₀/p_a)ρ_a = 4.65 × 10⁻⁴ g cm⁻³, w_h = (p_h/p_a) ρ_a = 1.07 × 10⁻⁴ g cm⁻³ and w_n = (p_n/p_a)ρ_a = 3.35 × 10⁻⁵ g cm⁻³.

The molecular weight of VEGF is 38 kDa (Frankel and Gillb, 2004). Hence, it can be shown that one molar of VEGF (1 M VEGF) is N_A × 38 kDa × mol/l = 36.5 g cm⁻³, where N_A = 6 × 10²³ mol⁻¹ is the Avogadro constant and 1 kDa = 1.66 × 10⁻²⁷ kg is the unified atomic mass unit. The VEGF threshold h₁ below which proliferation does not occur, in Chaplain (1995), was chosen to be h₁ ≤ 10⁻¹¹ M. Qualitatively similar results have been obtained in Chaplain (1995) for 0 ≤ h₁ ≤ 4 × 10⁻¹² M. Based on these estimates, we take h₁ = 10⁻¹¹ M = 3.65 × 10⁻¹⁰ g cm⁻³, but smaller values of h₁ do not qualitatively change our simulations.

2.6. Scaling parameters and volume fraction

It was observed in Eubank et al. (2008) that macrophages take up to 20% of the volume of the tumor. Hence, we take m₀ = 2 × 10⁸ cell cm⁻³.

Extracellular volume fraction information was derived from magnetic resonance imaging in Vincensini et al. (2007) for malignant and benign lesions in breast tumors. For the malignant lesions [invasive ductal carcinomas (IDC) and invasive lobular carcinomas (ILC)] the extracellular volume fractions were in the range of 0.50 ± 0.32 and 0:30 ± 0.22, respectively. In this work we will assume that initially, tumor cells occupy 70% of the volume of the tumor and that, on the average, the combined volume fractions of macrophages and tumor cells is 90%. Hence, θ = θ_c + θ_m = 0.9, where θ_c/θ_m = c₀/m₀.

To determine e₀ we assume that the average radius of the blood capillaries in normal tissue is 5 μm and parallel capillaries are 50 μm apart (Less et al., 1991). Then the density of the capillaries is 5²/50² = 10⁻² g cm⁻³. Since EC occupy only a fraction of this volume, we estimate the EC volume fraction to weight 10⁻²/4 = 2.5 × 10⁻³ g cm⁻³ (Lewis and Murdoch, 2005, p. 27); it follows that the EC density is e₀ = 2.5 × 10⁶ cell/cm⁻³. It has been shown in Less et al. (1991) that the mean capillary diameter in tumor is 10 μm, but the mean capillary distance in tumor is the same as in normal tissue. Based on this data we may assume that with angiogenesis, the maximal EC density inside the tumor e₁ is larger than in normal tissue, possibly by 2–3 times larger. We take e₁ = 2e₀ = 5 × 10⁶ cell cm⁻³. Sottnik et al. (2010) have shown that the EC fraction in tumors in 0.335%. Our estimate of 0.5% is comparable with this value.

MCP-1 concentrations in the range of 0.2–6.3 ng ml⁻¹ were reported in Owen and Sherratt (1997). M-CSF levels in breast tumors were measured in Ławicki et al. (2006), to be in the range of 134.5–1175.1 pg ml⁻¹, and VEGF levels in the range of 1–10 ng ml⁻¹ were observed in Eubank et al. (2008). Hence (similarly to Schugart et al., 2008), we take h₀ = 10 ng ml⁻¹ and choose the scaling parameters s₀,p₀,g₀ to be equal to h₀.

2.7. Proliferation and clearance/decay rates

Proliferation rates:

Tumor cells have a usual doubling time 18–24 h (Owen et al., 2004). Hence we take the doubling time of 19 h, so that λ₁ = (ln 2/19) h⁻¹ = 10⁻⁵ s⁻¹. The proliferation rate of endothelial cells is 0.02–0.056 h⁻¹ (Chaplain et al., 1995). Note that for small EC density e, the logistic term in Eq. (6) is approximately λ₅e(1−(e/e₁)) ≈ 2λ₅e. We take 2λ₅ = 0:05 h⁻¹, and hence, λ₅ = 7 × 10⁻⁶ s⁻¹.

Clearance/apoptosis rates:

The proliferation rate of tumor cells is larger than the death rate by apoptosis; we take μ_c = λ₁/2 = 5 × 10⁻⁶ s⁻¹. We assume that in the tumor periphery, the rate of clearance of dead cells (by macrophages; see Eq. (4)) is approximately the same as the rate of apoptosis of tumor cells, i.e., μ_bm₁ ≈ μ_c, where m₁ is the macrophage density as measured in Eubank et al. (2008) (see the boundary condition for macrophages in Section 2.1). Since m₁ = 10⁸ cell cm⁻³ (by Eubank et al., 2008), we get μ_b = 5 × 10⁻¹⁴ cm³ s⁻¹ cell⁻¹.

Decay rates:

The VEGF decay rate is μ_h = 0.456 h⁻¹, as in Plank et al. (2004). M-CSF is relatively stable, with a half-life of 3–4 h (Tang, 2000); hence, μ_s = (ln 2/4)h⁻¹ = 4.8 × 10⁻⁵ s⁻¹. The half-life of GM-CSF is between 10 and 14 h (Williams et al., 1999); we take μ_g = (ln 2/12) h⁻¹ = 1.6 × 10⁻⁵ s⁻¹. Finally, the MCP-1 decay rate is μ_p = 2 × 10⁻⁵ s⁻¹, as in Owen and Sherratt (1997).

2.8. Cytokine production rates

We will choose λ₆,λ₇,λ₉,λ₁₀ such that the corresponding dimensionless chemical production and decay rates are of the same order of magnitude (Owen and Sherratt, 1997).

VEGF production rate by tumor cells λ₆(w) in (7) and (8):

In Pyaskovskaya et al. (2008) the VEGF production rates were estimated for Lewis lung carcinoma in unfed culture over 5 days. VEGF production decreased from 35 to 5 pg/(10⁶ cells × h), thus giving a range of 10⁻²¹ −10²⁰ g s⁻¹ cell⁻¹. In Owen et al. (2004), the maximal production rate of a general chemoattractant (like VEGF and MCP-1) produced under hypoxia by tumor cells was taken to be 10⁻¹⁰d_a M, where d_a is the decay rate of the chemical and 10⁻¹⁰ M is its typical concentration. We remark that our μ_h is smaller than the value of d_a in Owen et al. (2004) since VEGF is assumed to decay more rapidly. If the molar concentration of VEGF in the standard density units is 36.5 g cm⁻³ and we use the VEGF decay rate μ_h from Table 2, then the rate of VEGF production is 4.6 × 10⁻¹³ g cm⁻³ s⁻¹, and dividing by c₀ = 7 × 10⁸ cell cm⁻³ from Table 2 we obtain the rate 6.57 × 10⁻²² g s⁻¹ cell⁻¹. Hence, we estimate the maximal VEGF production rate to be in the range of 6.57 × 10⁻²² −10⁻²⁰ g s⁻¹ cell⁻¹.

Studies have shown that the magnitude of induction of VEGF levels subjected to hypoxia varies with tissue type but generally falls between 2- and 4-fold. For example, 2–3-fold increase of VEGF in oral cell and lung carcinoma has been reported in Shang et al. (2006) and Koshikawa et al. (2003), 3–4-fold increase of VEGF in neuroblastoma (Rapella et al., 2002) and 2–4-fold increase of VEGF in overexpressed breast cancers in Braunstein et al. (2007). Hence, we take the maximal VEGF production rate in the hypoxic region to be four times larger than in the normoxic region and we choose 4λ₆ = 8.5 × 10⁻²² g s⁻¹ cell⁻¹ to be consistent with the estimated range of VEGF production rates.

VEGF production rate by macrophages λ₇(w) in (7) and (9):

Hypoxia is a stimulus for the VEGF expression in human monocytes, inducing up to 5-fold increase in the levels of VEGF (Melillo et al., 1999). VEGF production is also unregulated from macrophages when treated with M-CSF (Curry et al., 2008), about 2-fold compared to the unstimulated sample. The amount of VEGF secreted by macrophages is at least 2–3 times the amount secreted by tumor cells (Vicioso et al., 2006). Although VEGF levels by both tumor cells and macrophages are elevated during hypoxia, it is not clear as to which cell type produces more VEGF in the hypoxic regions. Based on Vicioso et al. (2006), we assume that in the normoxic region (w > w_h) the proportion of VEGF produced by macrophages and tumor cells is approximately 2.1, i.e., λ₇m₀ = 2λ₆c₀, but in the hypoxic region (w₁ < w < w_h) it is approximately 1.1, i.e., 2λ₇m₀ = 4λ₆c₀.

M-CSF production rate by tumor cells λ₉ in (10):

We compare the M-CSF production rate by tumor cells, λ₉, to the production rate, λ₆(w), of VEGF. The mRNA levels for VEGF and M-CSF from osteoclast differ in hypoxic and normoxic conditions; at normal oxygen levels M-CSF production is higher than VEGF and at low oxygen levels VEGF production is higher than M-CSF in Utting et al. (2010). In the absence of relevant studies for tumors that would compare M-CSF and VEGF production in normoxia, we assume that the same comparison holds for tumor cells, and take λ₉ = 1.5λ₆.

MCP-1 production rate by macrophages λ₁₀(w) in (12) and (13):

We take the normoxic basal level of MCP-1 production to be the same as the VEGF production by macrophages, i.e., λ₁₀ = λ₇. Since hypoxia inhibits the production of MCP-1 from macrophages about 2.5-fold compared to normoxia (Bosco et al., 2004), we take the MCP-1 production under hypoxic conditions to be 2/5λ₁₀.

2.9. Chemotactic, diffusion/dispersion and oxygen uptake/delivery rates

Chemotactic coefficients:

Similar to Section 2.5, where the molar concentration of VEGF (36.5 g cm⁻³) was shown, taking 10 kDa as the molecular weight of MCP-1 and 22 kDa as the molecular weight of GM-CSF, we obtain that the molar concentration of MCP-1 and GM-CSF is 10 g cm⁻³ and 22 g cm⁻³, respectively. The chemotactic coefficient for MCP-1 is in the range of 20–60 cm² s⁻¹ M⁻¹ (Schugart et al., 2008; Owen et al., 2004) and we take κ_p = 60 cm² s⁻¹ M⁻¹. The chemotactic coefficient for VEGF is κ_h = 36.5 cm² s⁻¹ M⁻¹, as in Schugart et al. (2008). In the absence of chemotactic data for GM-CSF, we assume κ_g to be comparable with κ_h, κ_p and take κ_g = 20 cm² s⁻¹ M⁻¹. The molar concentrations of VEGF, MCP-1 and GM-CSF allow us to write κ_h,κ_p,κ_g in the equivalent units cm⁵ g⁻¹ s⁻¹ in Table 2.

Oxygen consumption rates:

Oxygen consumption rates in murine macrophage-like RAW264.7 cells were measured in Nalwaya and Deen (2008) to be 32 ± 3 pmol/(10⁶ cells × s), typical of mammalian cells. Since the molar volume of oxygen is approximately 22.4 l/mol, this gives a range for λ₃ of 6.5 – 7.8 × 10⁻¹³ cm³ s⁻¹ cell⁻¹ and we choose λ₃ = 7 × 10⁻¹³ cm³ s⁻¹ cell⁻¹. In Girgis-Gabardo and Hassell (2008) the oxygen consumption rate by tumor cells was estimated to be 2.78 × 10⁻¹⁷ mol cell⁻¹ s⁻¹, thus giving a rate of 6.2 × 10⁻¹³ cm³ s⁻¹ cell⁻¹. However, older tumors harvested for 13–15 days showed smaller oxygen uptake rates in Butterworth and Cater (1967), even 50% smaller on day 15. Taking into account the Warburg effect (Chen et al., 2009), we assume that the total oxygen uptake by tumors cells is larger than by macrophages, possibly 2-fold larger. Hence, we take λ₄ = 2λ₃m₀/c₀ = 4 × 10⁻¹³ cm³ s⁻¹ cell⁻¹.

Oxygen delivery rates:

Since the oxygen level in tumor decreases as the tumor grows, the oxygen delivery by EC, λ₂e, is smaller than the oxygen consumed (primarily by tumor cells), so that λ₂e < λ₄wc, or, λ₂ < λ₄[wc/e]_average. We take λ₂ = c₀w₀ λ₄/(75e₀).

Diffusion/dispersion rates:

The diffusion rates D_c,D_m,D_w and the dispersion rate D_b are based on the values in the references from Table 2. Diffusion of endothelial cells is in the range of 10⁻¹² −10⁻¹⁰ cm² s⁻¹ (Owen et al., 2004; Plank et al., 2004) and we take D_e = 10⁻¹¹ cm² s⁻¹. In Owen et al. (2004) and Owen and Sherratt (1997) the diffusion rate of MCP-1 was 2 × 10⁻⁶ cm² s⁻¹; we take it to be D_p = 10⁻⁶ cm² s⁻¹. We assume that the diffusion rates of VEGF, M-CSF and GM-CSF are similar.

2.10. Sensitivity analysis

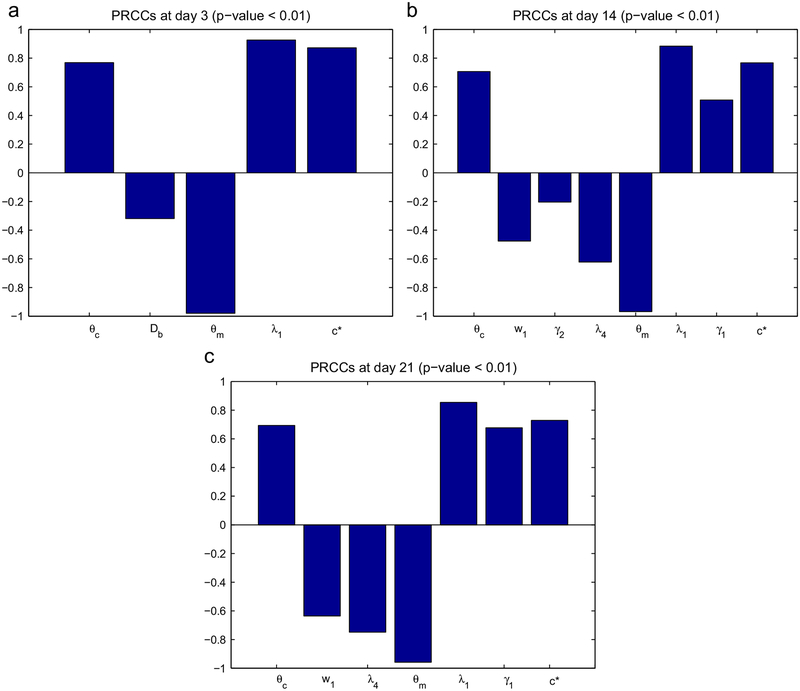
In the model developed in this paper there are a number of parameters which are estimated and may affect significantly the simulation results. We have chosen to test the following parameters: θ_c, D_b, w₁, λ₉, γ₂, λ₄, θ_m, λ₁, γ₁, c*. Although θ_c,θ_m,λ₁ have experimentally known ranges, these parameters have been included here, since they play an important role in our model. In order to see how sensitive the tumor radius is to these parameters (at days 3, 14 and 21), we have performed sensitivity analysis. We have chosen a range for each of these parameters and used Latin hypercube sampling to generate 200 samples. (The range of the tested parameters is given in Table 3, all other parameters are as in Table 2.) For each of the 10 parameters a partial rank correlation coefficient (PRCC) is calculated, the sign of which determines whether an increase in the parameter value will increase or decrease the tumor radius at a given time. The sensitivity analysis was carried out based on the method in Marino et al. (2008) and using the Matlab files available at http://malthus.micro.med.umich.edu/lab/usadata/.

Table 3.

Ten parameters chosen for sensitivity analysis and their ranges.

Parameter	Minimum	Baseline	Maximum	Units
θc	0.65	0.7	0.75
Db	5 × 10−11	10−10	5 × 10−10	cm2 s−1
w1	4.02 × 10−5	5.36 × 10−5	8.04 × 10−5	g cm−3
λ9	1.6 × 10−22	3.2 × 10−22	4.8 × 10−22	g s−1 cell−1
γ2	0	0.2	2	cm−1
λ4	2.86 × 10−13	4 × 10−13	5.14 × 10−13	cm3 s−1 cell−1
θm	0.15	0.2	0.25
λ1	8.02 × 10−6	10−5	1.07 × 10−5	s−1
γ1	1	2	4	cm−1
c*	9.1 × 108	9.45 × 108	9.8 × 108	cell cm−3

Out of the 10 parameters tested eight were statistically significant (p-value < 0.01) at day 14 (θ_c, w₁, γ₂, λ₄, θ_m, λ₁, γ₁, c*), seven at day 21 (θ_c, w₁, λ₄, θ_m, λ₁, γ₁, c*) and only five at day 3 (θ_c, D_b, θ_m, λ₁, c*). Fig. 1 shows the statistically significant PRCC values (p-value < 0.01) of the parameters of interest for R(t) at days 3, 14 and 21. We conclude that the tumor radius at days 14 and 21 is positively correlated to the parameters θ_c,λ₁,γ₁,c* and negatively correlated to w₁,λ₄,θ_m. In particular, R(t) increases if θ_c/θ_m increases and if the proliferation rate λ₁ increases.

Fig. 1.

Statistically significant PRCC values (p-value < 0.01) for R(t) at (a) day 3, (b) day 14 and (c) day 21.

3. Results

All simulations were carried out with MATLAB (version R2009a Mathworks). The model equations were numerically solved using pdepe (MATLAB function for initial-boundary value problems for parabolic-elliptic PDEs in 1D) in each time step. The ODE for the interface condition was calculated using an explicit second-order Runge–Kutta method.

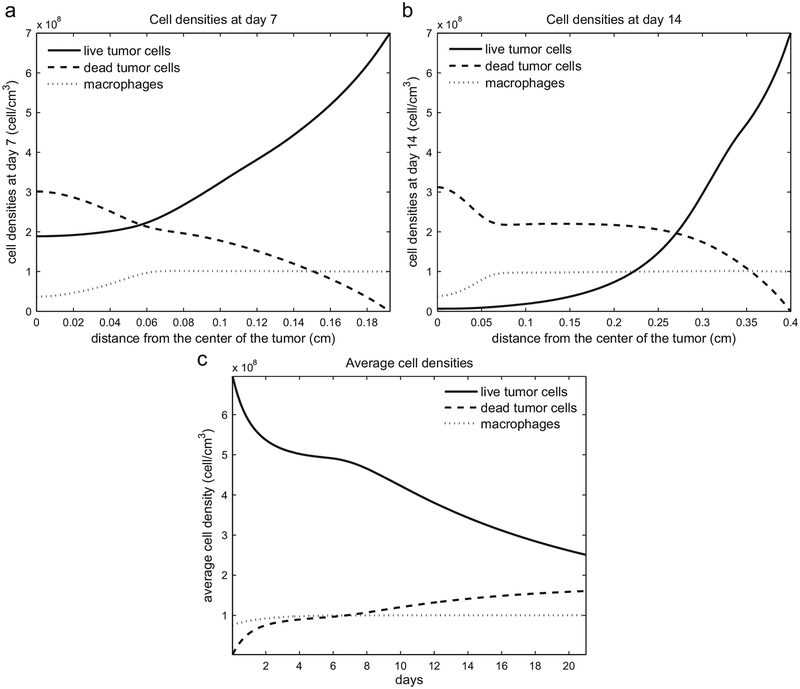
The spatial distribution of tumor cells (live and dead) and macrophages at days 7 and 14 are shown in Fig. 2(a) and (b). The density of live tumor cells increases toward the rim of the tumor, where there is more oxygen supply, whereas the density of the dead cell increases toward the center of the tumor where hypoxic conditions hold. Fig. 2(c) illustrates the evolution of the average tumor (live and dead) and macrophage densities over 21 days. Since most live tumor cells are near the rim, where the level of oxygen is high enough to keep them live and proliferating, the average density of these cell taken over the entire tumor decreases as the tumor increases; the reverse holds for the dead cells.

Fig. 2.

(a) Tumor cell (live and dead) and macrophage densities at day 7, when the tumor radius is 0.207 cm. (b) Tumor cell and macrophage densities at day 14, when the tumor radius is 0.41 cm. (c) Average cell densities over time.

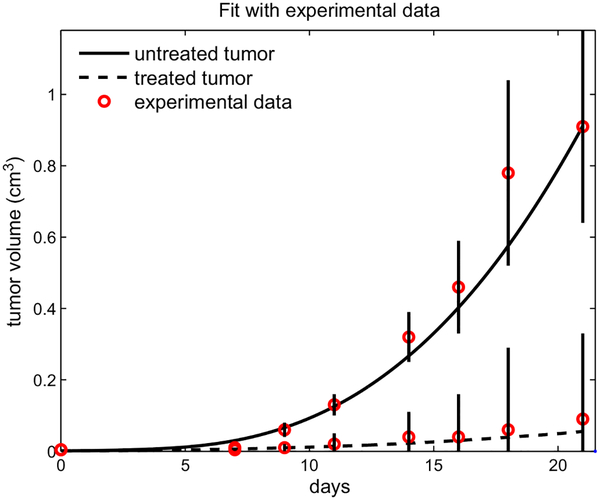
Fig. 3 shows the simulation results in two cases; no GM-CSF is given (the solid line) and 100 ng of GM-CSF administered three times a week: Monday, Wednesday and Friday (the dashed line). Experimental data from Eubank et al. (2008) in both cases are indicated by circles. The simulations fit well with the experimental data from Pollard (1997) in both cases. Indeed, the statistical precision of fit by the model was confirmed by a strong correlation coefficient between the experimental data and the simulation results (0.99 for the untreated and 0.988 for the GM-CSF treated case).

Fig. 3.

The volume of the treated and untreated tumor during 21 days. The circles and vertical lines correspond to experimental data and standard deviations from (Eubank et al., 2008).

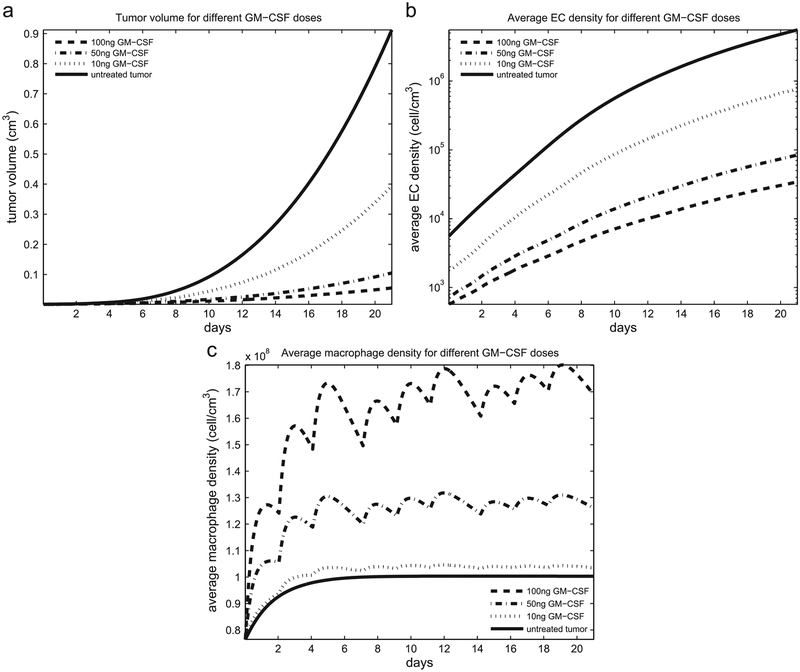
Fig. 4(a) simulates the tumor volume growth for different doses of GM-CSF (10, 50 and 100 ng) injected three times a week in equal volume. The 100 ng dose results in a 93.4% volume reduction compared to the volume of the untreated tumor. These results seem predictable as the highest dose of GM-CSF (100 ng) was most effective in tumor growth inhibition. It is interesting that this effect reaches a plateau as 10-fold more GM-CSF showed little effect on tumor growth in vivo (unpublished observation by coauthors Eubank and Roberts) driven by augmented receptor down-regulation on the macrophages. The average density of EC for the different doses of GM-CSF is shown in Fig. 4(b). Experimental data from Eubank et al. (2008) predict that the mean value of the average EC density at day 21 for the tumor treated by 100 ng of GM-CSF is 82% less than the mean value of the average EC density of the untreated tumor, while our model predicts a decrease in EC density by 89.8% at day 21 compared to the EC density of the untreated tumor for GM-CSF. This discrepancy may be attributed to several factors such as: (i) GM-CSF was not evenly distributed throughout the tumor, or (ii) the predicted half-life of GM-CSF is longer than 12 h.

Fig. 4.

(a) Tumor volume; (b) average endothelial cell density; (c) average macrophage density for different doses of GM-CSF.

Fig. 4(c) predicts macrophage density fluctuations which are GM-CSF dependent. At large doses of GM-CSF (100 ng per injection three times a week) the GM-CSF gradient in Eq. (11) becomes large and, as GM-CSF cleares up in 1–2 days, macrophage chemotaxis slows down. Experimental data from Eubank et al. (2008) show increased macrophage recruitment into the tumors after 21 days, but our model predicts a “fluctuating” migration of macrophages within the tumor treated by GM-CSF. We speculate that the fluctuation in macrophage density may arise from recruitment of macrophage precursor cells (monocytes) from the bone marrow upon GM-CSF injection into the tumor. GM-CSF is a known recruiter of white blood cells and has been used clinically to increase these cell numbers to help patients recover after bone marrow transplant.

Further, in vivo data suggest that the above macrophages are of an M1, tumor-fighting phenotype while macrophages in the PBS-treated tumors represent more of a tumor-helping, M2 phenotype (Eubank et al., 2008). This observation is intriguing because the presence of tumor macrophages in breast cancer patients predict poor prognosis (Lin and Pollard, 2004). Lin and Pollard (2004) have shown that the absence of TAMs did not change the incidence or growth of the primary tumor but decreased its rate of progression and inhibited metastasis. This is contrary to the finding in Eubank et al. (2008) which suggests that increases in tumor macrophage numbers in the presence of GM-CSF increases survival.

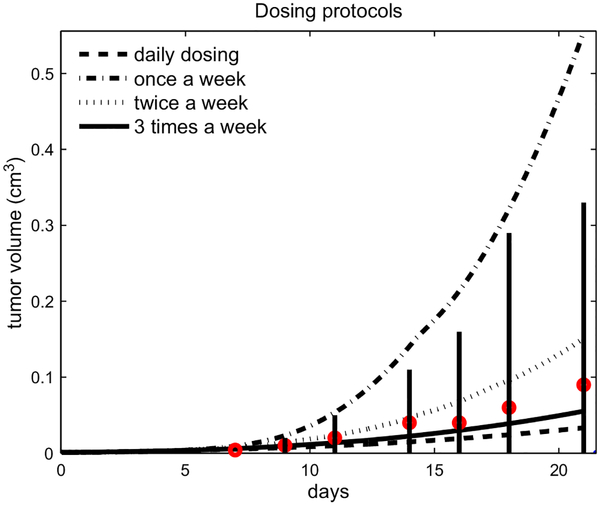
Our model can be used to evaluate the efficacy of different dosing protocols, while keeping the total amount of GM-CSF injected the same in the three week period (900 ng). Fig. 5 compares breast tumor growth from the following protocols: once a week (300 ng each Monday), twice week (150 ng each Monday and Thursday), three times a week (100 ng each Monday, Wednesday, and Friday), or daily (42.8 ng each day). Interestingly, our model predicts that when the total amount of GM-CSF delivered to the tumor is fixed (900 ng), a more frequent treatment is more effective. This ability to predict the effect of dosing schedules in therapy may help alleviate factors such as toxicity to the patients. For example, if higher doses of GM-CSF are not well tolerated, the dosage could be reduced and administered more frequently. Our model predicts that, with the half-life of GM-CSF at 12 h, changing treatment from a high dose of 300 ng once a week to 150 ng twice a week can reduce tumor growth by a factor of 3.66 after 3 weeks. We speculate that this improvement hinges mostly on the timed influx of macrophages and on the half-life of GM-CSF.

Fig. 5.

Comparing the tumor volume under different dosing protocols (daily, weekly, twice a week, three times a week) with the same total amount of GM-CSF in comparison with the experimental data from Eubank et al. (2008), where the dosing was three times a week.

4. Conclusion

M-CSF is over-expressed in most human breast cancers and triggers macrophages to produce biologically-active VEGF and MCP-1. MCP-1 attracts monocytes into the tumor which, in turn, differentiate into tumor-associated macrophages (TAMs). Thus, MCP-1 indirectly enhances the production of VEGF by TAM recruitment. TAMs have been shown to produce factors like MMPs and VEGF to induce new capillary formation from nearby blood vessels—feeding the tumor and enabling it to grow. The growth factor GM-CSF blocks the proliferative activity of VEGF on endothelial cells by stimulating mononuclear phagocytes to secrete soluble VEGF receptor-1 which sequesters VEGF and inhibits binding to its cognate receptors, VEGFR-1 and −2. Hence, GM-CSF may be considered as a potential therapy to block angiogenesis, thereby inhibiting tumor growth. Indeed, GM-CSF in combination with Herceptin is currently in phase II clinical study for treatment of invasive breast carcinoma (Herceptin and GM-CSF for metastatic breast cancer, M.D. Anderson Cancer Center, last updated 30 September 2010).

In this work, we develop a mathematical model which predicts the anti-angiogenic activity of GM-CSF. The model simulations correlate with experimental results for the PyMT mouse model of breast cancer. This work demonstrates the potential of mathematical modeling as a tool to generate hypotheses for successful treatment strategies of solid tumors. In this setting, our modeling predicts optimal dosing and administration scheduling of GM-CSF. Such information can be used to limit treatment toxicity for the patient. Studies are underway to validate this observation experimentally.

The model developed in this paper is based on interactions among several important variables which are involved in GM-CSF treatment of breast cancer in mice. This model could be further refined by including, more explicitly, interactions between macrophages and other immune cells like T cells, or other microenvironment elements like fibroblasts, or cytokines that drive a malignant transition. Observations learned from this study are already being utilized in the laboratory (by coauthor Eubank) to enhance treatment of human breast cancer in immunodeficient mice. Further, novel delivery methods for GM-CSF are being developed to limit the need for direct injections at the tumor site. For example, tests using GM-CSF-containing nanospheres which target macrophages are underway. Successful completion of these studies will pave the way for moving GM-CSF into human clinical trials for breast cancer.