A Bayesian Phase I/II Trial Design for Immunotherapy

Abstract

Immunotherapy is an innovative treatment approach that stimulates a patient’s immune system to fight cancer. It demonstrates characteristics distinct from conventional chemotherapy and stands to revolutionize cancer treatment. We propose a Bayesian phase I/II dosefinding design that incorporates the unique features of immunotherapy by simultaneously considering three outcomes: immune response, toxicity and efficacy. The objective is to identify the biologically optimal dose, defined as the dose with the highest desirability in the risk-benefit tradeoff. An Emax model is utilized to describe the marginal distribution of the immune response. Conditional on the immune response, we jointly model toxicity and efficacy using a latent variable approach. Using the accumulating data, we adaptively randomize patients to experimental doses based on the continuously updated model estimates. A simulation study shows that our proposed design has good operating characteristics in terms of selecting the target dose and allocating patients to the target dose.

1. Introduction

Cancer immunotherapy — treatments that harness and enhance the innate power of the immune system to fight cancer — represents the most promising new cancer treatment approach since the first chemotherapies were developed in the late 1940s (Couzin-Frankel, 2013; Topalian, Weiner, and Pardoll, 2011; Makkouk and Weiner, 2015). Immunotherapeutic approaches include the use of antitumor monoclonal antibodies, cancer vaccines, and nonspecific immunotherapies. These approaches stand to revolutionize the treatment of almost every kind of cancer (Couzin-Frankel, 2013; Kaufman, 2015).

Because of a vastly different functional mechanism, immunotherapy behaves differently from conventional chemotherapies. For conventional chemotherapies, it is reasonable to assume that efficacy and toxicity monotonically increase with the dose; however, this assumption may not hold for immunotherapy agents (IAs). As a result, traditional dose-finding designs that aim to identify the maximum tolerated dose (MTD) are not suitable for immunotherapy. To achieve optimal treatment effects, IAs are not necessarily administered at the MTD. In addition, immunotherapy often involves multiple endpoints (Topalian, Weiner, and Pardoll, 2011; Brody et al., 2011; Cha and Fong, 2011). Besides toxicity and efficacy (i.e., tumor response) outcomes, immune response is a unique and important outcome that is essential for the assessment of immunotherapy. Immune response measures the biological efficacy of IAs in activating the immune system, manifested by the proliferation of CD8+ T-cells, CD4+ T-cells and various cytokines (e.g., IFN-α, IL-1β, IL-6, IL-8). As immunotherapy achieves its therapeutic effect by activating the immune system, it is critical to incorporate the immune response in the trial design and leverage its close relationship with clinical endpoints (i.e., efficacy and toxicity) for efficient and practical decision making. Pardoll (2012) described several studies that showed that post-treatment immune responses correlate with clinical outcomes.

Our research is motivated by an immunotherapy trial that aims to find the optimal dose of a novel anti-programmed death 1 (PD-1) immune checkpoint inhibitor for treating patients with recurrent, chemoresistant ovarian cancer. The PD-1 pathway is a negative feedback system that represses Th1 cytotoxic immune responses. This pathway is up-regulated in many tumors and in their surrounding microenvironment. Blocking this pathway with antibodies to PD-1 or its ligands has led to remarkable clinical responses in patients with many different types of cancer, including melanomas and non-small-cell lung cancer. Five dose levels (0.1, 0.3, 0.5, 0.7, 0.9 mg/kg) of the inhibitor will be investigated and the prepared doses will be administered by slow injection over 10 minutes. A maximum of 60 patients will be accrued to the trial. Patient efficacy response is characterized as complete response (CR), partial response (PR), stable disease (SD), or progressive disease (PD) based on the Response Evaluation Criteria in Solid Tumors. CR is defined as the disappearance of all target lesions. PR is defined as a decrease of at least 30% in the sum of the diameters of target lesions, taking as a reference the baseline sum of the diameters. PD is defined as an increase of at least 20% in the sum of the diameters of target lesions, taking as a reference the smallest sum measured during the study. SD is defined as having neither a sufficient decrease in lesion sizes to qualify as PR, nor sufficient increase to qualify as PD. The immune response of primary interest is the number of CD8+ T-cells measured in the tumor biopsy at the end of the first cycle (28 days) of treatment. Previous studies suggest that the immune response is expected to be associated with the efficacy of the treatment (Sato, et al., 2005; Ercolini, et al., 2005; Hamanishi, et al., 2007; Bachmayr-Heyda, et al., 2013). Dose-limiting toxicity is defined as grade 3 or higher toxicity as scored using the NCI Common Toxicity Criteria for Adverse Events.

We developed a novel phase I/II trial design to find the biologically optimal dose (BOD) for immunotherapy, where BOD is defined as the dose yielding the highest risk-benefit tradeoff, which is formally defined in Section 2.4. In the design, we simultaneously consider three endpoints, including immune response, tumor response and toxicity. To capture the distinct features and relationships among the three endpoints, we model the marginal distribution of the immune response using the Emax model; and conditional on the immune response, we model the joint distribution of the binary toxicity outcome and the ordinal efficacy outcome through a latent variable approach. We elicit the numerical utility to quantify the desirability of the dose based on the risk-benefit tradeoff. During the trial, based on the accumulating data, we update the model estimates and assign a new patient to the dose with the highest desirability through adaptive randomization.

There is a rich body of literature on phase I/II trial designs that integrate the conventional phase I and II segments of clinical drug development trials by simultaneously considering toxicity and efficacy. Thall and Russell (1998) developed a phase I/II trial design that characterizes patient outcomes using a trinary ordinal variable to account for both toxicity and efficacy. Gooley et al. (1994) discussed a phase I/II design in bone marrow transplantation trials to determine a dose that balances the risks of two complications. Braun (2002) proposed the bivariate continual reassessment method, in which the MTD is based jointly on toxicity and disease progression. Thall and Cook (2004) described a Bayesian design based on tradeoffs between toxicity and efficacy probabilities. Yin et al. (2006) proposed a Bayesian phase I/II design based on the odds ratio of efficacy and toxicity. Yuan and Yin (2009, 2011) developed a time-to-event phase I/II design to accommodate late-onset toxicity and efficacy, and a Bayesian phase I/II design for drug-combination trials. Jin et al. (2014) proposed a general strategy to handle delayed toxicity and efficacy outcomes for phase I/II trials using Bayesian data augmentation. Guo and Yuan (2015) proposed a phase I/II design that accommodates informative dropouts. Liu and Johnson (2016) developed a phase I/II design without assuming parametric dose-toxicity and dose-efficacy curves. Comprehensive coverage of phase I/II designs is provided in the book of Yuan, Nguyen and Thall (2016). To the best of our knowledge, this article provides the first phase I/II design for immunotherapy trials that jointly accounts for immune response, toxicity, and efficacy.

The remainder of this article is organized as follows. In Section 2, we present the joint probability model for the continuous immune response, binary toxicity and ordinal efficacy outcomes, and the dose-finding algorithm. In Section 3, we examine the operating characteristics of the proposed design through simulation studies. We provide concluding remarks in Section 4.

2. Method

Probability Models

Consider a phase I-II trial with J prespecified doses, d < · · · < dj, under investigation. Let Y_T denote the binary toxicity outcome, with Y_T = 1 indicating toxicity (or severe adverse events), and = 0 otherwise. Let Y_E denote the tumor response, which is often classified as CR, PR, SD, or PD. Although CR and PR are generally more desirable, in immunotherapy, SD is often regarded as a positive response because some immunotherapies prolong survival by achieving durable SD without notable tumor shrinkage. Thus, we define Y_E as a trinary ordinal outcome, with Y_E = 0,1, and 2 indicating PD, SD and PR/CR, respectively. As described previously, besides Y_T and Y_E, an essential endpoint for immunotherapy is immune response. Let 17 denote a measure of the immune response (e.g., the count of CD8+ T-cells or the concentration of cytokine), which takes a real value after appropriate transformation. The outcome used for dose finding in our approach is a trinary vector Y = (Y_I,Y_T,Y_E). In contrast, most existing phase I/II designs are based on only (Y_T,Y_E). Thall et al. (2014) proposed a phase I/II design to optimize the sedative dose given to preterm infants using three clinical outcomes.

Adaptive decisions in the trial (e.g., dose assignment and selection) are based on the behavior of Y as a function of dose d. To reflect the fact that in immunotherapy, clinical responses rely on the activation of the immune system, we factorize the joint distribution [Yi,Y_T,Y_E | d] into the product of the marginal distribution of Yi and the conditional distributions of Y_T and Y_E as follows,

$$\left[Y_I,Y_T,Y_E|d,\mathit{\theta }\right]=\left[Y_I|d,{\mathit{\theta }}_1\right]\left[Y_T,Y_E|d,Y_I,{\mathit{\theta }}_2\right],$$

where θ is the vector of the parameters, and θ₁ and θ₂ are subvectors of θ. For notational brevity, we suppress arguments θ₁ and θ₂ when it will not cause confusion.

We model the marginal distribution [Y_I | d] using an Emax model,

$$Y_I|d={\alpha }_0+\frac{{\alpha }_1{d}^{{\alpha }_3}}{{\alpha }_2^{{\alpha }_3}+d^{{\alpha }_3}}+\epsilon ,$$

where a₀ is the baseline immune activity in the absence of the IA; α₁ is the maximum immune activity that is possibly achieved by the IA above the baseline activity, often known as E_max; α₂ is the dose that produces half of the maximum immune activity (i.e., ED₅₀); α₃ is the Hill factor that controls the steepness of the dose-response curve; and ε is the random error, which is normally distributed with a mean of 0 and variance σ², i.e., ε ~ N(0, σ²).

Modeling the joint distribution of [Y_T,Y_E | d,Y_I] is more complicated because Y_T and Y_E are different types of variables, i.e., Y_T is a binary variable whereas Y_E is an ordinal variable, and they are correlated. To this end, we take the latent variable approach. Specifically, let Z_T and Z_E denote two continuous latent variables that are related to Y_T and Y_E, respectively, as follows,

$$Y_T=\{\begin{array}{cc}0& \mathrm{if}{Z}_T<{\zeta }_1\\ 1& \mathrm{if}{Z}_T\ge {\zeta }_1\end{array}\mathrm{and}{Y}_E=\{\begin{array}{lll}0& \mathrm{if}& Z_E<{\xi }_1\\ 1& \mathrm{if}& {\xi }_1\le Z_E<{\xi }_2\\ 2& \mathrm{if}& Z_E\ge {\xi }_2\end{array},$$

where ζ₁, ξ₁ and ξ₂ are unknown cutpoints. Z_T and Z_E can be interpreted as the patient’s latent traits, and Y_T and Y_E are the clinical manifestations of unobserved Z_T and Z_E. When Z_T and Z_E pass certain thresholds, certain clinical outcomes (e. g., toxicity, CR/PR) are observed. We assume that [Z_T, Z_E| d,Y_I] follows a bivariate normal distribution

$$\left(\begin{array}{c}{Z}_T\\ Z_E\end{array}\right)|Y_I,d\sim N_2\left(\left(\begin{array}{c}{\mu }_T\left(Y_I,d\right)\\ {\mu }_E\left(Y_I,d\right)\end{array}\right),\left(\begin{array}{cc}{\sigma }_{11}& {\sigma }_{12}\\ {\sigma }_{12}& {\sigma }_{22}\end{array}\right)\right),$$

Where μ_K(Y_I, d) = E(Z_k|Y_I, d), k = E or T, is the conditional mean of Z_k.

Specification of μ_T(Y_I, d) and μ_Ε(Y_I, d) requires some consideration. Immune activity is a normal biological phenomenon consistently occurring in the human body; thus, it is typically expected that a low or normal level of immune activity will not cause any immune-related toxicity and that severe immune-related toxicity will occur only when the therapy-induced immune response exceeds a certain threshold. To account for such a threshold effect, we model the relationship between m_T (Y_I, d) and Y_I and d as

$${\mu }_T\left(Y_I,d\right)={\beta }_0+{\beta }_{1}d+I\left(Y_I>{\beta }_3\right){\beta }_2{Y}_I,$$

where β₀,β₁,β₂ and β₃ are unknown parameters, and the indicator function I(Y_I > β₃) = 1 when Y_I > β₃, and 0 otherwise. Under this model, Y_I induces toxicity only when it passes threshold β₃. Because we do not expect the immune response to be the sole cause of toxicity, in (5), we include dose d as a covariate to capture other possible treatment-related toxicity.

To model the mean structure μ_Ε(Y_I, d) for efficacy, we assume a quadratic model,

$${\mu }_E\left(Y_I,d\right)={\gamma }_0+{\gamma }_1{Y}_I+{\gamma }_2{Y}_I^2,$$

where the quadratic term is used to accommodate the possibility that efficacy may not monotonically increase with the immune response. In practice, μ_Ε(Y_I,d) may first increase with YI and then plateau after YI reaches a certain value. Although the quadratic model cannot directly take an increasing-then-plateau shape, it works reasonably well in that case in our numerical study (i.e., scenarios 6 and 7 in Table 1). This may be because our goal is not to accurately estimate the whole immune-response curve, but to use (6) as a “working” model to obtain a reasonable local fit to guide the dose escalation and deescalation. As the quadratic model can provide good approximation to the plateau (e.g., by taking a slowly increasing shape) locally around the current dose, it leads to appropriate dose transition and selection. In addition, as the Emax model (2) allows Y_I to plateau with the dose d, the efficacy model (6) indeed accommodates the case that efficacy Y_E plateaus with d.

Table 1:

Utility based on toxicity, efficacy and immune response.

Toxicity	Immune response	Efficacy
		PD (YE = 0)	SD (YE = 1)	CR/PR (YE = 2)
No (YT = 0)	Desirable (ỸI = 1)	5	70	100
	Undesirable (ỸI = 0)	0	50	80
Yes (Yt =1)	Desirable (ỸI = 1)	0	20	45
	Undesirable (ỸI = 0)	0	10	35

In equation (6), we assume that conditional on Y_I, Y_E is independent of dose d to reflect the consideration that the treatment effect of immunotherapy is mostly mediated by the immune response. For cases in which such an assumption may not be true, we can add d as a covariate in the model. Because latent variables Z_T and Z_E are never observed, to identify the model, we set ζ₁ = ξι = 0, σ₁₁ = 𝜎₂₂ = 1 and accordingly constrain 0 < σ₁₂ < 1 in (4).

Prior Specification

The prior specification of the parameters in [Y_I | d] is facilitated by their intuitive interpretations described previously. We elicit prior estimates of (α₀,₁,α₂,α₃) from clinicians, denoted as ${\widehat{\alpha }}_j$, j = 0, · · ·, 3, and assign α_j an independent Gamma distribution with mean ${\widehat{\alpha }}_j$ and variance $T_j^2$. We set T_j at a relatively large value (e.g., $4{\widehat{\alpha }}_j$) to obtain a vague prior. Because of taking a vague prior approach, we do not require the prior estimate ${\widehat{\alpha }}_j$ to be accurately specified. The primary objective of eliciting ${\widehat{\alpha }}_j$ is to obtain a ballpark estimate of these parameters so that the prior is appropriately centered to avoid extreme (e.g., very small or large) estimates that may lead to inappropriate actions (e.g., terminate the trial too early or escalate the dose too quickly) at the beginning of the trial when data are sparse. As the trial proceeds, the accumulating data will dominate the vague prior and guide dose transition. The simulation described later shows that our design is not sensitive to the specification of ${\widehat{\alpha }}_j$. We assign σ² a vague inverse Gamma prior distribution, e.g., σ² ~ IG(0.1, 0.1).

To specify the prior distribution for the parameters that appear in [Y_T,Y_E| d,Y_I], we take the regularized vague prior approach (Gelman et al., 2008; Guo and Yuan, 2017). Conventional noninformative priors with huge variances work well for moderate and large samples, but are often problematic for small samples, such as in early phase trials, causing numerical instability and pathological posterior inference (Yuan, Nguyen and Thall, 2016). To obtain reliable inference, the prior should be vague enough to cover the plausible values of the parameter, but not too vague to cause stability issues. Gelman et al. (2008) proposed regularizing the prior using the fact that in practice, a typical change in an input variable is unlikely to lead to a dramatic change in the probability of the response variable. In our case, Y_T and Y_E marginally follow probit models after integrating out latent variables Z_T and Z_E. A change of 2.5 on the probit scale moves the probability of the outcome variable from 0.01 to 0.5 or from 0.5 to 0.99, which is considered unlikely for a typical change in a covariate. Therefore, we scale the input variables (i.e., d and 17) to have mean 0 and standard deviation 0.5, and assign each of the regression coefficients (i.e., β₁,₂,γ₁,γ₂) an independent normal prior N(0,1.25²), such that a change in any of these covariates from one standard deviation below the mean to one standard deviation above the mean most likely results in a difference of less than 2.5 on the probit scale. The same normal prior is used for the intercepts β₀ and γ₀, under which a two-standard-deviation change in these parameters moves the outcome probability from 1% and 99% when covariates are set at their mean values. As toxicity is typically non-decreasing with the dose and immune response, it might seem more sensible to use a positive-valued prior, e.g., a gamma or truncated normal prior, to restrict the values of β₁ and β₂ to be positive. However, when done, this actually hurts the performance of the design, especially for the immunotherapy agents for which toxicity increases slowly with the dose. For these agents, the true values of β₁ and β₂ are close to 0. Because the gamma or truncated normal prior has most of its mass spanning the positive real line, using them tends to inflate the estimates of β₁ and β₂, especially at the beginning of the trial when data are sparse, which hinders dose escalation. In the case that toxicity increases rapidly with the dose, using the gamma or truncated normal prior does not have this issue because the true values of β₁ and β₂ are away from 0. The simulation results comparing the performance of the design under different priors are provided in the Supplementary Materials.

We assign β₃ (i.e., the threshold of immune response for inducing toxicity) a uniform prior distribution β₃ ~ Unif (a₁, a₂), with $a_1<{\widehat{\alpha }}_0\mathrm{and}{a}_2>{\widehat{\alpha }}_0+{\widehat{\alpha }}_1,$ to cover the plausible range of immune response. We assign the correlation parameter σ₁₂ a uniform prior Unif (0,1), and latent variable cutoff parameter ξ₂ ~ Unif (0, b), where b is chosen to cover the practical range of Pr(Y_E < 2) (i.e., the probability of PD and SD).

Likelihood and Posterior

Let N denote the maximum trial sample size. For the ith patient, denote the observed outcome by y_i = (yi,i, y_T,i, y_E,i) and the assigned dose by d_[i], where i = 1,..., N. Integrating over (Z_T,_i, Z_E,_i) and defining (ζ₀ = ξ₀ = —œ, ζ₂ = ξ₃ = ∞, the likelihood for the observables of the ith patient is given by

$$\begin{gathered} L\left({\mathit{y}}_i|d_{\left[i\right]},\mathit{\theta }\right)=f\left(y_{I,i}|d_{\left[i\right]},{\mathit{\theta }}_1\right)\mathrm{Pr}(Y_{T,i}=y_{T,i},Y_{E,i}=y_{E,i}|y_{I,i},d_{\left[i\right]},{\mathit{\theta }}_2) \\ =f\left(y_{I,i}|d_{\left[i\right]},{\mathit{\theta }}_1\right)\mathrm{Pr}({\zeta }_{y_{T,i}}\le Z_{T,i}<{\zeta }_{y_{T,i}+1},{\xi }_{y_{{}_{E,i}}}\le Z_{E,i}<{\xi }_{y_{{}_{E,i}}+1}|y_{I,i},d_{\left[i\right]},{\mathit{\theta }}_2) \\ =f\left(y_{I,i}|d_{\left[i\right]},{\mathit{\theta }}_1\right){\displaystyle {\int }_{{\zeta }_{y_{T,i}}}^{{\zeta }_{y_{T,i}+1}}{\displaystyle {\int }_{{\xi }_{y_{{}_{E,i}}}}^{{\xi }_{y_{{}_{E,i}}+1}}f\left(Z_{T,i},Z_{E,i}|Y_{I,i},d_{\left[i\right]},{\mathit{\theta }}_2\right)\mathrm{d}}}{Z}_{T,i}\mathrm{d}{Z}_{E,i} \end{gathered}$$

Let n = 1, …, N denote an interim sample size when an adaptive decision is to be made during the trial, and ${\mathcal{D}}_n=({\mathit{y}}_1\dots ,{\mathit{y}}_n)$ denote the observed data from the first n patients. The likelihood for the first n patients in the trial is $L\left({\mathcal{D}}_n|\mathit{\theta }\right)={\prod }_{i=1}^{n}L\left({\mathit{y}}_i|d_{\left[i\right]},\mathit{\theta }\right).$

Let (θ) denote the joint prior distribution of θ. The joint posterior distribution based on the data from the first n patients is $p(\mathit{\theta }|{\mathcal{D}}_n)\propto L({\mathcal{D}}_n|\mathit{\theta }(p(\mathit{\theta })$. We sample from this posterior distribution using the Markov chain Monte Carlo algorithm with Gibbs sampler (Robert and Casella, 2004).

Desirability of Dose

For each individual endpoint Y_I, Y_T or Y_E, the evaluation of the desirability of a dose is straightfoward. We prefer a dose that has low toxicity, strong immune response and high objective response. However, when we consider (Y_I,Y_T,Y_E) simultaneously, the evaluation of the desirability of a dose becomes more complicated. We need to consider the risk-benefit tradeoffs between the undesirable and desirable clinical outcomes, as physicians routinely do in almost all medical decisions when selecting a treatment for a patient. A convenient tool to formalize such a process is to use a utility function U(Y_I,Y_T,Y_E) to map the multidimensional outcomes into a single index to measure the desirability of a dose in terms of the risk-benefit tradeoffs. The utility should be elicited from physicians and/or patients to reflect medical practice. This approach has been used in previous trial designs (Houede, et al., 2010; Thall, et al., 2013; Thall, et al., 2014; Yuan, Nguyen and Thall, 2016; Guo and Yuan, 2017; Murray, et al., 2017).

Based on our experience, a convenient way of eliciting U(Y_I,Y_T,Y_E) that works well in practice is as follows: we first dichotomize the immune response Y_I as desirable (${\tilde{Y}}_I$ = 1) or undesirable (${\tilde{Y}}_I$ = 0) based on a cutoff C_r specified by clinicians (i.e., ${\tilde{Y}}_I$ = 1 if Y_I ≥ C_I, and 0 otherwise), and fix the score of the most desirable outcome (i.e., desirable immune response, no toxicity and CR/PR) asU(${\tilde{Y}}_I$ = 1, Y_T = 0, Y_E = 2) = 100 and the least desirable outcome (i.e., undesirable immune response, toxicity and PD) as U(${\tilde{Y}}_I$ = 0, Y_T = 1,Y_E = 0) = 0. Using these two boundary cases as the reference, we then elicit the scores for other possible outcomes from clinicians, which must be located between 0 and 100. An example of elicited utility is given in Table 1. Note that the purpose of dichotomizing Y_r here is to simplify the elicitation of utilities from clinicians. Our model and inference are based on the original scale of Y_I. If desirable, Y_I can be categorized into more than two levels, which allows us to account for the desirability of Y_I at a finer scale, but at the cost of slightly increasing the logistic burden for utility elicitation. For example, if we categorize Y₁ into three levels (e.g., low, median, or high), a total of 18 utility values are required to be elicited from clinicians.

Although Y_E and Y_I are generally positively correlated, there are several benefits to considering both of them when constructing the utility. First, immunotherapy achieves its therapeutic effect of killing cancer cells by activating the immune response, and the tumor response Y_E (i.e., a short-term endpoint) may not be a perfect surrogate of the longterm treatment effect of the immunotherapy, e.g., progression-free survival (PFS) or overall survival time. Thus, when two doses have similar Y_E and Y_I, we often prefer the dose that has higher potency to activate the immune response, which is potentially translated into better long-term treatment efficacy. Second, using Y_E and Y_I simultaneously improves the power to identify the optimal dose. For example, given two doses with (Pr(Y_E > 0) = 0.3, E(Y_I) = 20) and (Pr(Y_E > 0) = 0.4, E(Y_I) = 60), respectively, the second dose is more likely to be identified as more desirable when we use (Y_I, Y_E) rather than Y_E only, because the difference in the value of Y_I is much larger than that of Y_E between the two doses.

Constructing the utility requires close collaboration between statisticians and clinicians, and should be customized for each trial to best reflect the clinical needs and practice. For example, if Y_E is the long-term efficacy endpoint of interest (e.g., PFS) or Y_j is believed to have little impact on the clinical desirability of the dose (after considering Y_E), we may prefer to define the utility using only (Y_E,Y_T), while ignoring Y_I. Although the elicitation of utility seems rather involved, in our experience, the process actually is quite natural and straightforward. For many trials, this may be done by simply explaining what the utilities represent to the principal investigator (PI) during the design process, and asking the PI to specify all necessary values of U(Y_I,Y_T,Y_E) after fixing the scores for the best and worst elementary outcomes as described previously. After the initial values of utility are specified, comparing outcomes that have the same or similar numerical utilities often motivates the PI to modify the initial specification. In our experience, clinicians quickly understand what the utilities mean, since they reflect actual clinical practice. After completing this process and simulating the trial design, it then may be examined by the PI. In some cases, the simulation results may motivate slight modification of some of the numerical utility values, although such modification typically has little or no effect on the design’s operating characteristics. One possible criticism for using the utility values is that they require subjective input. However, we are inclined to view this as a strength rather than a weakness. This is because the utilities must be elicited from the physicians planning the trial, and thus their numerical values are based on the physician’s experience in treating the disease and observing the good and bad effects that the treatment has on the patients. The process of specifying the utility requires physicians to carefully consider the potential risks and benefits of the treatment that underlie their clinical decision making in a more formal way and incorporate that into the trial. In addition, our simulation study and previous studies show that the design is generally not sensitive to the numerical values of the utility as long as it reflects a similar trend.

For a given dose d, its true utility is given by

$$E\left(U\left(d\right)|\mathit{\theta }\right)={\displaystyle \int U\left({\tilde{Y}}_I,Y_T,Y_E\right)f}\left({\tilde{Y}}_I,Y_T,Y_E|d,\mathit{\theta }\right)\mathrm{d}{\tilde{Y}}_I\mathrm{d}{Y}_T\mathrm{d}{Y}_E.$$

Since θ is not known, the utility of dose d must be estimated. Given interim data D_n collected from the first n patients at a decision-making point in the trial, the utility of dose d is estimated by its posterior mean

$$E\left(U\left(d\right)|{\mathcal{D}}_n\right)={\displaystyle \int E\left(U\left(d\right)|\mathit{\theta }\right)p\left(\mathit{\theta }|{\mathcal{D}}_n\right)\mathrm{d}\mathit{\theta }}.$$

This posterior mean utility will be used to measure the desirability of a dose and guide dose escalation and selection.

Let π_T = Pr(Y_T = 1|d) denote the toxicity rate and n_E = Pr(Y_E > 0|d) denote the response rate of SD/PR/CR. Let ϕ_T denote the upper limit of the toxicity rate, and ϕ_Ε denote the lower limit of the response rate, specified by physicians. We define the BOD as the dose with the highest utility while satisfying π_T < ϕ_T and π_Ε > ϕ_Ε.

Dose Admissibility Criteria

A practical issue is that a dose that is “optimal” in terms of the utility alone may be unacceptable in terms of either safety or the response rate. To ensure that any administered dose has both an acceptably high success rate and an acceptably low adverse event rate, based on interim data D_n, we define a dose d as admissible if it satisfies both the safety requirement

$$Pr\left({\pi }_T<{\varphi }_T|{\mathcal{D}}_n\right)>C_T$$

and the efficacy requirement

$$Pr\left({\pi }_E>{\varphi }_E|{\mathcal{D}}_n\right)>C_E,,$$

where C_T and C_E are prespecified toxicity and efficacy cutoffs. We denote the set of admissible doses by A_n. Because the objective of the admissible rules (9) and (10) is to rule out doses that are excessively toxic or inefficacious, in practice we should set C_T and C_E at small values, such as C_T = C_E = 0.05, which could be further calibrated through simulation. To see this point, it is useful to state the two rules in the following equivalent forms: a dose is unacceptable or inadmissible if Pr(π_T > ϕ_T|D_n) > 1 — C_T = 0.95 or Ρr(π_Ε < ϕ_Ε|D_n) > 1 — C_E = 0.95. This says that the dose is unacceptable if it is either very likely to be inefficacious or very likely to be too toxic. If we set C_T and C_E at large values, then the design is very likely to stop the trial early with all doses declared inadmissible due to the large estimation uncertainty at the beginning of the trial; see page 62 of the book by Yuan, Nguyen and Thall (2016) for more discussion on this issue. In the Supplementary Materials, we report the results from a simulation study we conducted that confirmed this issue.

Dose-finding Algorithm

Based on the above considerations, our dose-finding algorithm is described formally as follows. Assume that patients are treated in cohorts of size m with the maximum sample size of N = m x R. We allow m =1 such that patients are treated one by one. The first cohort of patients is treated at the lowest dose d₁. Assume that r cohort(s) of patients have been enrolled in the trial, where r =1, · · ·, R — 1. Let d_h denote the current highest tried dose, C_es denote the probability for escalation based on toxicity, and n = m x r. To assign a dose to the (r + 1)th cohort of patients:

1. If the posterior probability of toxicity at d_h satisfies Pr(π_T(d_h) < ϕ_T|D_n) > C_es and d_h ≠ d_J, then we treat the (r + 1)th cohort of patients at d_h+1. In other words, if the current data show that the highest tried dose is safe, we want to continue to explore the dose space by treating the next cohort of patients at the next higher new dose.

2. Otherwise, we identify the admissible set A_n and adaptively randomize the (r + 1)th patient or cohort of patients to dose dj ∈ A_n with probability

$${\psi }_{j,n}=\mathrm{Pr}[U\left(d_j\right)=\max \{U(d_{j^{\prime }}),j^{\prime }\in {\mathcal{A}}_n\}|{\mathcal{D}}_n],$$

which is the posterior probability that dose j is the optimal dose having the highest posterior mean utility. We restrict the randomization in admissible dose set A_n to avoid treating patients at doses that are futile or overly toxic. If A_n is empty, the trial is terminated.

1. Once the maximum sample size of N is exhausted, the dose in A_N with the largest posterior mean utility E(U(d)|D_N) is recommended.

In step 2, to assign a patient to a dose, we use adaptive randomization rather than the greedy algorithm that always assigns the patient to the dose with the currently highest estimate of utility. This is because the latter method tends to become stuck at the local optima and leads to poor precision for identifying the BOD. Adaptive randomization provides a coherent mechanism to avoid that issue and improve the operating characteristics of the design (Yuan, Nguyen, and Thall, 2016).

3. Simulation

We assessed the performance of our proposed design using simulation studies. Taking the setting of the motivating trial, we considered five doses (0.1, 0.3, 0.5, 0.7, 0.9), with a maximum sample size of 60 in a cohort size of 3. The toxicity upper bound ϕ_T= 0.3 and efficacy lower bound ϕ_E= 0.3. Rescaled by the prior estimate of the baseline immune response, we set ${\widehat{\alpha }}_0=1,{\widehat{\alpha }}_1=5,{\widehat{\alpha }}_2=0.5\mathrm{and}{\widehat{\alpha }}_3=2$ based on the prior estimates of E_max, ED₅₀, and the steepness of the dose-response relationship elicited from clinicians. We set $T_j=4{\widehat{\alpha }}_j$ to obtain vague priors forα_j, j = 0, 3, so that the prior standard deviation was 4 times the prior mean. Since the estimates of the baseline and the maximum immune response were ${\widehat{\alpha }}_0=1$ ${\widehat{\alpha }}_0+{\widehat{\alpha }}_1=6,$ respectively, we assigned β₃ (i.e., the threshold of immune response for inducing toxicity) a uniform prior β₃ ~ Unif (0, 9) to cover the whole plausible range, and ξ₂ a uniform prior Unif (0, 6) to cover a reasonable range of Pr(Y_E < 2) that may be encountered in practice. For example, when Pr(Y_E = 0) = 0.1, the range for Pr(Y_E < 2) is (0.1, 0.999) under this prior. Calibrated by simulation, we took the probability cutoffs C_T = C_E = 0.05 for defining admissible doses and C_es = 0.5 for dose escalation. The utility elicited from physicians is displayed in Table 1. The same prior distribution, probability cutoffs, and utility were used throughout the simulation. We designed 8 scenarios that varied in the number of target doses, location of the target doses, as well as the patterns of toxicity, efficacy, and immune response (see Table 2). Figure 1 shows the true dose-response curves for immune response, toxicity and efficacy for these scenarios. Under each scenario, we simulated 1,000 trials.

Table 2:

True immune response, toxicity, efficacy probabilities, and utility at each dose, and selection percentage and the average number of patients treated at each dose level under the proposed design and the EffTox design. The boldface numbers are the target doses.

	dose level
	1	2	3	4	5
	Scenario 1
E(YI )	2.0	2.9	4.5	5.7	6.3
πT	0.03	0.04	0.1	0.17	0.23
(πE,1, πE,2)†	(0.46, 0.11)	(0.50, 0.13)	(0.35, 0.07)	(0.16, 0.02)	(0.08, 0.01)
Utility	30.9	34.6	26.2	13.1	8
Selection % (proposed)	0.282	0.649	0.069	0	0
# of patients	16.0	16.9	13.9	9.0	4.8
Selection % (EffTox)	0.476	0.521	0.001	0	0.002
# of patients	17.4	16.3	13.1	8.2	4.4
	Scenario 2
E(YI)	2.0	2.9	4.5	5.7	6.3
πT	0.03	0.07	0.19	0.35	0.49
(πE,1, πE,2)	(0.28, 0.14)	(0.31, 0.17)	(0.31, 0.18)	(0.28, 0.14)	(0.25, 0.11)
Utility	24.2	27.8	30.6	23.8	17.7
Selection % (proposed)	0.117	0.094	0.736	0.047	0.006
# of patients	13.0	14.0	14.6	10.9	7.4
Selection % (EffTox)	0.212	0.602	0.183	0.001	0.002
# of patients	14.2	15.2	14.4	10.1	6.2
	Scenario 3
E(YI )	2.0	2.9	4.5	5.7	6.3
πT	0.07	0.09	0.12	0.3	0.49
(πE,1, πE,2)	(0.16, 0.04)	(0.17, 0.05)	(0.22, 0.07)	(0.25, 0.10)	(0.27, 0.12)
Utility	9.8	11.9	19.7	22.1	20.1
Selection % (proposed)	0.028	0.005	0.29	0.572	0.057
# of patients	9.5	9.8	15.0	15.1	9.2
Selection % (EffTox)	0.143	0.103	0.254	0.255	0.203
# of patients	11.1	12.0	13.0	12.9	9.8
	Scenario 4
E(YI )	2.0	2.9	4.5	5.7	6.3
πT	0.16	0.16	0.16	0.16	0.16
(πE,1, πE,2)	(0.21, 0.06)	(0.26, 0.09)	(0.34, 0.17)	(0.36, 0.20)	(0.37, 0.22)
Utility	12.0	17.7	32.8	40.2	42.3
Selection % (proposed)	0.000	0.000	0.006	0.257	0.735
# of patients	7.9	8.7	12.4	15.3	15.6
Selection % (EffTox)	0.008	0.004	0.046	0.207	0.733
# of patients	9.3	10.6	12.4	13.4	14.3
	Scenario 5
E(YI )	2.6	3.4	3.9	4.3	4.6
πT	0.05	0.12	0.2	0.28	0.36
(πE,1, πE,2)	(0.15, 0.09)	(0.22, 0.15)	(0.24, 0.17)	(0.23, 0.16)	(0.21, 0.15)
Utility	13.8	21.9	24.5	23.7	20.6
Selection % (proposed)	0.024	0.036	0.431	0.42	0.077
# of patients	11.6	12.8	13.0	12.3	10.0
Selection % (EffTox)	0.002	0.258	0.711	0.017	0.002
# of patients	11.4	14.7	14.4	11.2	7.8
	Scenario 6
E(YI )	2.6	3.4	3.9	4.3	4.6
πT	0.01	0.04	0.09	0.14	0.2
(πE,1, πE,2)	(0.24, 0.06)	(0.31, 0.10)	(0.34, 0.12)	(0.35, 0.13)	(0.36, 0.13)
Utility	17.3	24.9	28.3	29.6	29.4
Selection % (proposed)	0.016	0.001	0.098	0.401	0.483
# of patients	10.4	11.1	12.1	13.1	13.2
Selection % (EffTox)	0.024	0.094	0.43	0.321	0.129
# of patients	10.3	12.1	12.9	12.7	11.8
	Scenario 7
E(YI )	2.6	3.4	3.9	4.3	4.6
πT	0.16	0.16	0.16	0.16	0.16
(πE,1, πE,2)	(0.16, 0.37)	(0.16, 0.37)	(0.16, 0.37)	(0.16, 0.37)	(0.16, 0.37)
Utility	32.5	34.3	36.9	38.5	39.7
Selection % (proposed)	0.175	0.021	0.038	0.091	0.675
# of patients	11.9	11.8	12.2	11.9	12.2
Selection % (EffTox)	0.351	0.086	0.146	0.07	0.347
# of patients	13.2	12.0	11.4	11.5	11.9
	Scenario 8
E(YI )	2.5	3.1	3.5	3.8	3.9
πT	0.72	0.78	0.84	0.88	0.91
(πE,1, πE,2)	(0.06, 0.04)	(0.08, 0.06)	(0.09, 0.06)	(0.09, 0.07)	(0.10, 0.08)
Utility	2.4	3.5	4.1	4.7	5.2
Selection % (proposed)	0	0	0	0	0
# of patients	4.3	3.2	3.1	1.7	0.7
Selection % (EffTox)	0	0	0	0	0
# of patients	4.1	3.0	2.7	2.0	0.8

^†π_E,₁ = Pr(Y_E = 1), and π_E,2 = Pr(Y_E = 2). ²⁴

Figure 1: Dose-response curves for the 8 scenarios in the simulation study.

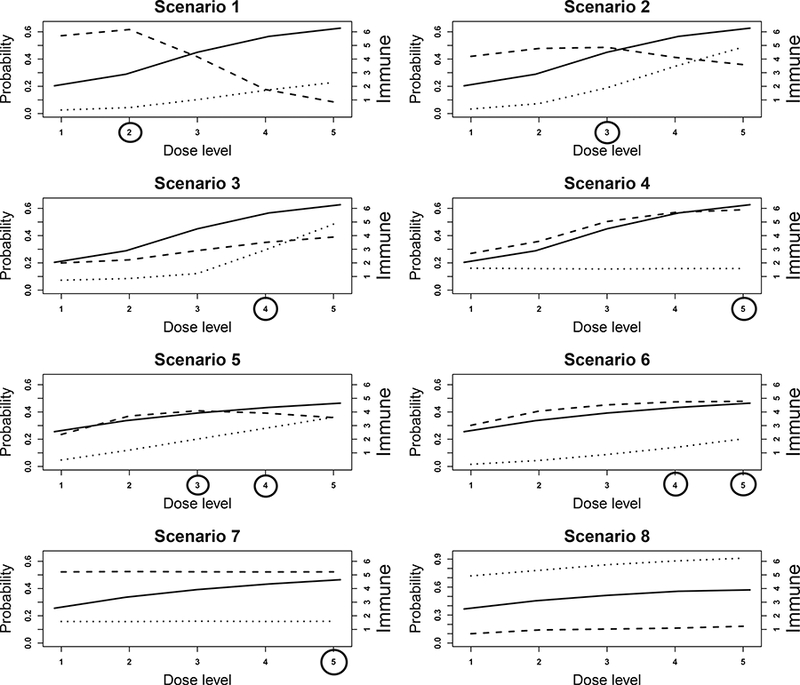
The dotted, dashed, and solid lines are the toxicity (π_t), efficacy (π_E), and immune response (E(Y_I)) curves, respectively. Toxicity and efficacy are plotted against the left y-axis, and the immune response is plotted against the right y-axis. Target doses are indicated by circles.

We compared our design with a design that considers only efficacy and toxicity (denoted as the EffTox design), as in most existing phase I/II designs such as that of Thall and Cook (2004). To make the comparison more meaningful, we used the same toxicity and efficacy models as the proposed design, but with the immune response term dropped such that

$${\mu }_T\left(d\right)={\beta }_0+{\beta }_{1}d$$

$${\mu }_E\left(d\right)={\gamma }_0+{\gamma }_{1}d+{\gamma }_2{d}^2.$$

The risk-benefit utility used in the EffTox design was obtained by averaging U(Y_j,Y_T,Y_E) in Table 1 over Y_j.

Table 2 summarizes the operating characteristics of our proposed design and the EffTox design. Scenarios 1 to 4 consider the case with one target dose and different shapes of dose- toxicity and dose-efficacy curves. In scenarios 1 and 2, the efficacy probabilities first increase and then decrease with the dose; in scenario 3, both toxicity and efficacy increase with the dose; and in scenario 4, toxicity remains constant across the doses, and efficacy increases with the dose.

In scenario 1, the target dose is dose level 2. Dose level 1 has similar toxicity probability as dose level 2, but lower efficacy probabilities. By taking advantage of the immune response data, the proposed design has higher power to distinguish these two doses. The percentage of correct selection of the target dose under the proposed design is 12.8% higher than that under the EffTox design. The number of patients allocated to the target dose is similar between the two designs. In scenario 2, dose level 3 is the target dose that is safe and has the highest utility. Our proposed design correctly identified the target dose 73.6% of the time, and allocated the largest number of patients to the target dose (i.e., 14.6) among the 5 doses. In contrast, the EffTox design selected the target dose only 18.3% of the time because it ignored the immune response. Dose levels 2 and 3 have similar efficacy, but level 3 has a much higher immune response and thus is more desirable. Because of ignoring the immune response, the EffTox design failed to recognize that dose level 3 is better. For a similar reason, the proposed design also outperformed the EffTox design in scenario 3, under which the target dose is level 4. The percentage of correct selection of the target was 57.2% under the proposed design, and only 25.5% under the EffTox design. The proposed design also assigned more patients to the target dose. In scenario 4, the dose-toxicity curve is flat and the two designs performed comparably.

Scenarios 5 and 6 were designed to have two target doses. In scenario 5, efficacy first increases and then decreases, whereas in scenario 6, efficacy first increases then plateaus. In these two scenarios, the proposed design performed well, with the combined percentage of correct selection of the two target doses exceeding 85%. In contrast, the percentage of correct selection of the target doses under the EffTox design was 72.8% and 45%, respectively. Scenario 7 considers a special case in which five doses have the same toxicity and efficacy probabilities, but higher doses induce a stronger immune response and thus have higher utility or desirability. The target dose is level 5. The proposed design selected the target dose 67.5% of the time, whereas the EffTox design selected the target dose 34.7% of the time. In scenario 8, the toxicity is higher than the toxicity upper bound ϕ_E = 0.3 and the efficacy is lower than the efficacy lower bound ϕ_Ε = 0.3 at all dose levels. Across 1000 simulations, the trial was terminated early 100% of the time under both designs.

3.1. Sensitivity Analyses

We carried out sensitivity analyses to assess the robustness of the performance of our proposed design by using 1) another set of utility values, and 2) a smaller sample size. Compared to the utility in Table 1, the new utility (see Table 3) assigns higher scores (i.e., less penalty) to Y_T = 1 (toxicity), that is, patients are willing to tolerate higher toxicity to attain higher efficacy. The simulation results (see Table 4) show that the proposed design performed well, with high percentages of correct selection of the target doses. When the maximum sample size dropped from 60 to 42, the performance of our design was slightly worse, as summarized in Table 5, but the selection percentage of the target dose was still the highest among all doses.

Table 3:

Utility for sensitivity analysis.

Toxicity	Immune response	Tumor response
		PD (YE = 0)	SD (YE = 1)	CR/PR (YE = 2)
No (YT = 0)	Desirable (ỸI = 1)	10	70	100
	Undesirable (ỸI = 0)	5	50	80
Yes (Yt =1)	Desirable (ỸI = 1)	5	40	60
	Undesirable (ỸI = 0)	0	30	55

Table 4:

Simulation results with an alternative utility.

	dose level					dose level
	1	2	3	4	5	1	2	3	4	5
	scenario 1					scenario 2
Selection %	0.23	0.67	0.1	0	0	0.081	0.05	0.785	0.079	0.005
# of patients	15.6	15.5	14.0	9.6	5.4	12.6	13.3	14.6	12.0	7.6
	scenario 3					scenario 4
Selection %	0.011	0.004	0.194	0.616	0.135	0.008	0	0.009	0.261	0.722
# of patients	9.6	10.1	14.2	15.0	9.8	8.7	9.2	12.5	14.3	15.4
	scenario 5					scenario 6
Selection %	0.013	0.017	0.291	0.533	0.117	0.002	0.001	0.031	0.266	0.695
# of patients	11.3	12.2	12.6	12.3	10.7	10.4	11.2	12.0	13.0	13.2
	scenario 7					scenario 8
Selection %	0.126	0.013	0.038	0.106	0.717	0.000	0.000	0.000	0.000	0.000
# of patients	11.9	11.9	11.7	11.9	12.6	4.3	3.2	2.9	2.1	0.8

Table 5:

Simulation results with a maximum sample size of 42.

	dose level					dose level
	1	2	3	4	5	1	2	3	4	5
	scenario 1					scenario 2
Selection %	0.375	0.491	0.132	0	0	0.178	0.105	0.633	0.078	0.006
# of patients	10.6	10.5	9.6	6.8	4.4	9.5	9.5	9.6	7.9	5.5
	scenario 3					scenario 4
Selection %	0.042	0.008	0.309	0.489	0.108	0.004	0.005	0.014	0.258	0.719
# of patients	7.1	7.4	9.7	10.0	7.2	6.5	6.7	8.5	9.8	10.5
	scenario 5					scenario 6
Selection %	0.067	0.041	0.305	0.452	0.117	0.034	0.016	0.088	0.321	0.539
# of patients	8.6	8.7	8.9	8.3	7.3	7.2	7.9	8.6	9.0	9.2
	scenario 5					scenario 6
Selection %	0.185	0.031	0.036	0.093	0.655	0.000	0.000	0.000	0.000	0.000
# of patients	9.0	8.2	8.0	8.0	8.8	4.3	3.2	2.9	2.1	0.8

Our prior specification requires elicitation of prior estimates of άs from clinicians. Given the incipient stage of research in immunotherapy, these estimates may not be very reliable. To evaluate the robustness of our proposed design to different values of these prior estimates, we performed sensitivity analysis with two alternative prior estimates of α’s: $\left({\widehat{\alpha }}_0,{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3\right)=\left(2,4,0.4,3\right)$ or $\left({\widehat{\alpha }}_0,{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3\right)=\left(1.5,6,0.6,2.5\right).$ As shown in Figure 2, the results are similar across different prior estimates of α′s, suggesting that our design is not sensitive to the prior estimates of α′s. Detailed results are provided in the Supplementary Materials.

Figure 2: Sensitivity analysis with three different prior estimates of α′s in scenarios 1–4.

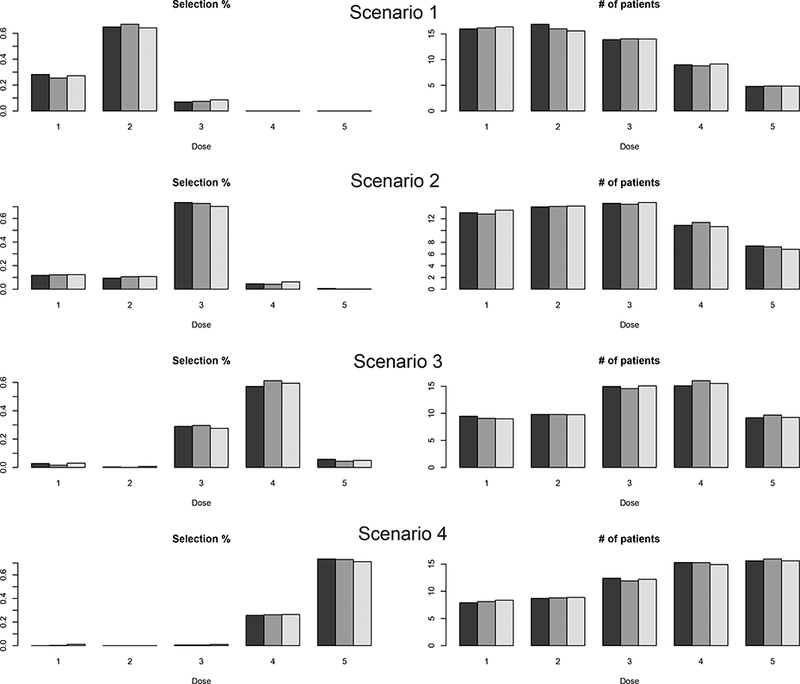
In each plot, at each dose level, the three bars from left to right correspond to the results with prior estimates $\left({\widehat{\alpha }}_0,{\widehat{\alpha }}_1,{\widehat{\alpha }}_2,{\widehat{\alpha }}_3\right)$ = ( 1, 5, 0.5, 2), (2, 4, 0.4, 3), and (1.5, 6, 0.6, 2.5), respectively.

Finally, we evaluated the sensitivity of the proposed design to different prior distributions. We made all the priors more non-informative. Specifically, for α′s, we set the prior standard deviation to five times the prior mean, i.e., $T_j=5{\widehat{\alpha }}_j.$ To σ², we assigned an inverse Gamma prior with parameters 0.01, i.e., σ² ~ 1G(0.01,0.01). The regression coefficients β₁,₂, γ₁, γ ₂ were assigned normal prior N(0, 2.5²) so that the prior standard deviation was twice the previous value. The simulation results are very similar to the original results (see Figure 3), suggesting that our design is not sensitive to the prior distributions.

Figure 3: Sensitivity analysis with two different prior distributions of model parameters under scenarios 1–4.

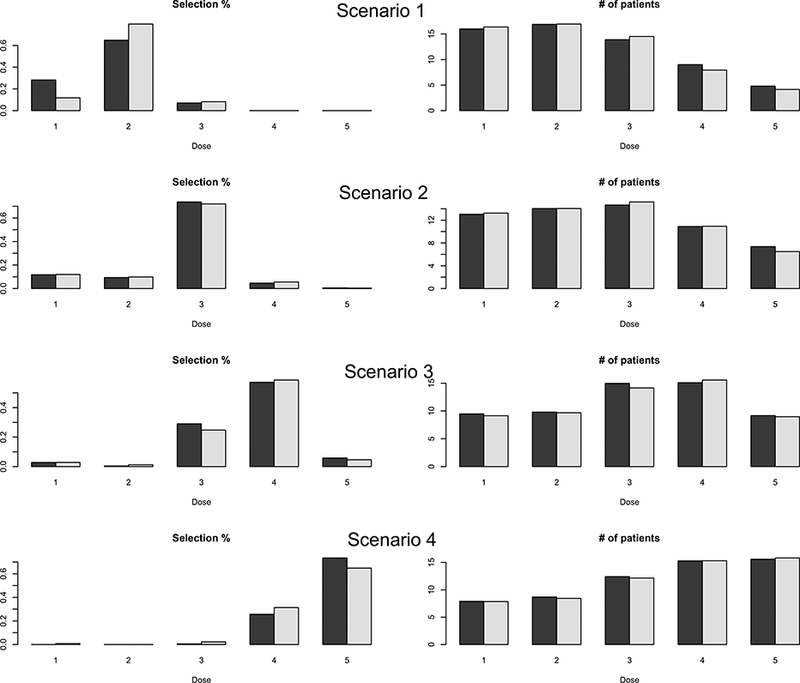
In each plot, at each dose level, the two bars represent the results under two different prior distributions.

4. Discussion

We have proposed a Bayesian phase I/II clinical trial design for immunotherapy by simultaneously considering immune response, toxicity and efficacy. We use an Emax model for the marginal distribution of the immune response and a latent variable approach to model the joint distribution of the binary toxicity and ordinal efficacy outcomes conditional on the immune response. Based on these three outcomes, utility is used to quantify the desirability of the dose and make the decision of dose assignment and selection. Our simulation study shows that the proposed design has desirable operating characteristics.

In order to capture the important features of immune response, toxicity, and efficacy, and the interplay among the three endpoints, our model has a relatively large number of parameters. One concern may be that at the inception of the trial, data are sparse and the parameter estimates are highly variable and mainly driven by the prior. However, this does not cause issues because the number of investigational doses is typically small (e.g., < 8 doses) and our dose-finding algorithm does not allow for skipping untried doses for dose escalation. At the beginning of the trial when the parameter estimates are highly variable, the dose-finding algorithm acts somewhat “semi-randomly” by trying the doses sequentially from low to high, guided largely by the priors. Actually, in some anti-intuitive sense, such uncertainty and “randomness” are helpful because it provides the design freedom to move around and explore the dose space, and to avoid being stuck at a local dose. When the trial proceeds and data accumulate, we obtain more reliable estimates and the dose assignment becomes more stable and converges to the target dose. Therefore, as long as at the middle or late stage of the trial, we have adequate data to make reasonable estimates, we are likely to make the correct dose assignment and select the target dose at the end of the trial. In addition, the primary objective of the phase I/II trial is to identify the optimal dose among a set of prespecified doses, not to obtain accurate estimates. This also renders the design higher tolerance to the variability of parameter estimates. As long as the method obtains the rank of estimated desirability correctly, it will correctly select the target dose.

In this article, ordinal tumor response is used as the efficacy endpoint. In some immunotherapy trials, the PFS time may be a more appropriate endpoint to quantify the therapeutic efficacy of the treatment. To accommodate these cases, we can model the joint distribution of the immune response, toxicity and PFS as follows: first model the marginal distribution of immune response using the Emax model; conditional on the immune response, model the conditional distribution of a binary (or ordinal) toxicity outcome using a logistic (or multinomial) model; and then conditional on both the immune response and toxicity, model the conditional distribution of PFS using a survival regression model, e.g., proportional hazards model (Cox, 1972).