Figure 1.

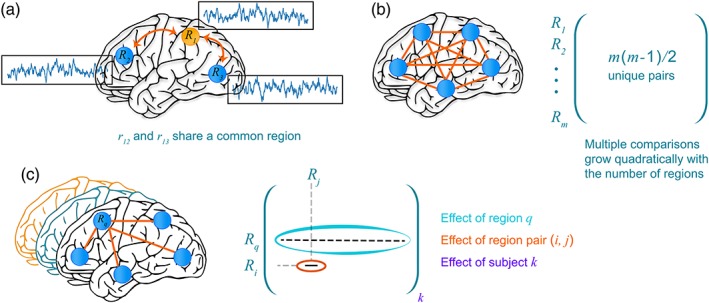
Characterizing the inter‐region correlation structure of group brain data. (a) Correlations between two pairs of brain regions, r _ij, are not independent when they share a common region. Thus, when simultaneously estimating multiple correlations, such relatedness needs to be modeled and accounted for. (b) Estimating correlations leads to a multiplicity problem, in particular how to account for the simultaneous inferences of all effects in conventional hypothesis testing. In a Bayesian framework, multiplicity relates to the problem of estimating all correlations simultaneously by invoking the notion of multilevel “information sharing,” also known as partial pooling or shrinkage. (c) Within a Bayesian multilevel framework, it is possible to frame the problem in terms of estimating the population‐level effect of (1) brain region, R _q, (2) RP, r _ij, and (3) subject k. The estimation of the contribution of the effect of brain regions is a unique contribution of our framework, which allows investigators to characterize a region's “importance” within a principled statistical framework [Color figure can be viewed at http://wileyonlinelibrary.com]