Structure–function multi‐scale connectomics reveals a major role of the fronto‐striato‐thalamic circuit in brain aging

Abstract

Physiological aging affects brain structure and function impacting morphology, connectivity, and performance. However, whether some brain connectivity metrics might reflect the age of an individual is still unclear. Here, we collected brain images from healthy participants (N = 155) ranging from 10 to 80 years to build functional (resting state) and structural (tractography) connectivity matrices, both data sets combined to obtain different connectivity features. We then calculated the brain connectome age—an age estimator resulting from a multi‐scale methodology applied to the structure–function connectome, and compared it to the chronological age (ChA). Our results were twofold. First, we found that aging widely affects the connectivity of multiple structures, such as anterior cingulate and medial prefrontal cortices, basal ganglia, thalamus, insula, cingulum, hippocampus, parahippocampus, occipital cortex, fusiform, precuneus, and temporal pole. Second, we found that the connectivity between basal ganglia and thalamus to frontal areas, also known as the fronto‐striato‐thalamic (FST) circuit, makes the major contribution to age estimation. In conclusion, our results highlight the key role played by the FST circuit in the process of healthy aging. Notably, the same methodology can be generally applied to identify the structural–functional connectivity patterns correlating to other biomarkers than ChA.

1. INTRODUCTION

Aging is a dynamical process that encompasses a systemic time‐dependent decline on multiple scales from biological to psychological and social levels. Interestingly, individuals with the same chronological age (ChA) might exhibit different trajectories of age‐related biological deterioration, as measured by biomarkers of functional performance, tissue integrity, and metabolic health (Khan, Singer, & Vaughan, 2017; Steves, Spector, & Jackson, 2012). This mismatch reflects two different concepts of age. One is ChA, calculated as the time running as birth, whereas the other is the biological age, which, irrespective of birth year, is based on the level of biological maturation at a given time. The mismatch between chronological and biological aging has gained major scientific interest in the past years due to its potential implication for health and disease of age‐related molecular, genetic, cellular and organ‐specific dynamics and their genetic, epigenetic, and environmental modulators (Jia, Zhang, & Chen, 2017). Indeed, it is well established that aging is a major risk factor for most of the late‐onset diseases such as cancer, cardiovascular disease, diabetes, and neurodegenerative diseases (Fulop et al., 2010).

In relation to brain biological aging, psychophysical, neuropsychological, and physiological studies support that functional performance of the brain declines with age, with an impact on cognition (long‐term and working memory, executive functions, conceptual reasoning, and processing speed; Grady, 2012; Park et al., 1996), mood (anxiety and depression; Knight & Durbin, 2015), circadian behavior (disruption of amplitude and period length), and sleep cycle (poor sleep quality and delayed sleep onset latency; Kondratova & Kondratov, 2012).

These changes in brain performance occur in parallel with well‐established age‐related macrostructural and microstructural brain variations. At the microstructural level, age has been associated with alterations in synaptic structures (decreased synaptic density and synaptic terminals), aggregation of abnormal proteins outside and inside neurons, such as plaques and tangles, reduced neurogenesis and synaptic plasticity, abnormal increase of astrocytes and oligodendrocytes, altered myelination, and reduction of nerve growth factor concentration (LaPoint et al., 2017; Peters, 2002; Price & Morris, 1999). However, whether aging reduces the number of neurons is still under debate, as several post‐mortem human and primate studies support that the cortical cell number remains unchanged (Morrison & Hof, 1997), suggesting that neuronal shrinkage occurring along the lifespan (rather than cell loss) is the main process underlying brain atrophy.

At the macroscopic level, both global and regional atrophies are the most reported characteristics of the aging brain, supported by several post‐mortem and MRI studies. Neuroimaging studies have shown that the overall brain volume varies with age in an “inverted‐U” fashion, increasing volume in about 25% from childhood to adolescence, then remaining constant for about three decades to finally decay down to childhood size at late ages (Courchesne et al., 2000). This pattern of age‐related brain atrophy along the lifespan has been associated with the deterioration of cognitive performance in the healthy population (Ritchie et al., 2015). Of note, age‐related gray and white matter atrophies are not homogeneous, with higher atrophy observed in white matter as compared to cortical gray matter (Jernigan et al., 2001; Resnick, Pham, Kraut, Zonderman, & Davatzikos, 2003) and regionally, with more prominent atrophy in hippocampus (West, 1993), prefrontal and parietal cortices (Raz et al., 1997; Salat et al., 2004; Sullivan & Pfefferbaum, 2007). In contrast, the volume of the cerebrospinal space (ventricles, fissures, and sulci) increases with age (Resnick et al., 2003).

Modern techniques such as diffusion tensor imaging (DTI) have allowed the in vivo inspection of age‐related structural connectivity (SC) to show (in agreement with histological findings) a cortical disconnection (de Groot et al., 2016; Mårtensson et al., 2018), which triggers a decrease of functional integration of some of the cognitive networks (Grady, 2012; O'Sullivan et al., 2001). Several DTI studies in healthy aging support an association between white matter atrophy and a widespread degeneration of white matter fibers, with age‐related changes predominantly affecting frontal tracts (O'Sullivan et al., 2001) and gradually extending to posterior tracts (Davis et al., 2009), a pattern that inverts the sequence of myelination during early brain development and that supports the “last‐in‐first‐out principle” for white matter deterioration along the lifespan.

The development of resting and task‐based functional MRI (fMRI) has provided in vivo functional correlates to the observed age‐related atrophy and SC brain disconnection, showing consistently age‐related regional changes in the patterns of brain activation, with decreased activity in the occipital lobe and increased activity in the frontal lobe across a variety of tasks (Grady, 2012). Functional connectivity (FC) studies at rest have gone a step further and demonstrated that aging not only induces regional brain activity changes but also a decrease in FC of large‐scale brain networks, specifically between anterior and posterior regions, including superior and middle frontal gyrus, posterior cingulate, middle temporal gyrus, and the superior parietal region (Andrews‐Hanna et al., 2007; Damoiseaux et al., 2008).

The combination of SC and FC analyses by complex network approaches have led to the conceptualization of brain networks as a connectome (Feldt, Bonifazi, & Cossart, 2011; Sporns, 2011), and its correlates with age and disease has gained major attention in fundamental neuroscience (Crossley et al., 2014). Complex network approaches have highlighted the key role played by several network features in aging and brain diseases, such as network hubness, node efficiency, network modularity, and hierarchical organization. The effects of aging on network modularity have shown a decrease in network segregation along the lifespan (Chan, Park, Savalia, Petersen, & Wig, 2014; King et al., 2017; Song et al., 2014), a mechanism supporting the loss of functional specialization at the cognitive level (Chan, Alhazmi, Park, Savalia, & Wig, 2017).

Moreover, combined SC and FC analyses have suggested that not only segregation (i.e., network modularity) decreases with age but integration (i.e., node efficiency) increases (Hagmann et al., 2010) in a counterbalanced manner that ensures network efficiency along the lifespan. Others, however, have suggested that small‐worldness and network modularity remain stable along the lifespan, despite a considerable reduction in the number of white matter tracts connecting different regions (Lim, Han, Uhlhaas, & Kaiser, 2015). Analyses of longitudinal data, less abundant than cross‐sectional data, have shown that the brain maps of FC variations by age do not match well with the maps of SC (Fjell et al., 2017), highlighting that FC and SC are affected by age in a more independent manner than previously thought.

The combined FC and SC analyses also have revealed that the deterioration of the cortical to subcortical connections plays a key role for the integration of several resting state networks underlying cognitive processes, such as executive function, processing speed, and memory (Ystad et al., 2011). By calculating node‐degree distributions, other studies have shown an age‐related connectivity reduction of network hubs (Betzel et al., 2014), supporting the hypothesis that the alteration of network hubs might trigger brain aging similar to what occurs in a plethora of other brain pathologies (Crossley et al., 2014).

Very recently, new computational strategies such as machine learning have been applied to the process of aging. In particular, a new paradigm denominated brain‐predicted age (BPA) has been introduced to quantify the mismatch between age‐associated brain alterations and ChA. Very striking, the use of BPA have been already used in different diseases, including traumatic brain injury (Cole et al., 2015), mild cognitive impairment (MCI) and Alzheimer's disease (Gaser, Franke, Klöppel, Koutsouleris, & Sauer, 2013), HIV infection (Cole, Underwood, et al., 2017), and schizophrenia (Schnack et al., 2016). A critical issue in all these studies is the selection of an adequate approach to achieve the highest robustness and precision for the mismatch quantification between chronological and brain ages. Very strikingly, the combined rather than separate analysis of SC and FC has shown to provide a better estimation of ChA (Zimmermann et al., 2016).

Although previous studies have addressed BPA by separate or combined analyses of SC and FC, none of them has proposed an optimal method that, applying multi‐scale complex network analysis to the structural–functional connectome, simultaneously identifies age‐related brain changes while calculating BPA. In this study, we extend previous work (Cole, Underwood, et al., 2017; Cole et al., 2015; Cole, Ritchie et al., 2017; Dosenbach et al., 2010; Franke, Ristow, & Gaser, 2014; Franke et al., 2010; Gaser et al., 2013; Han, Peraza, Taylor, & Kaiser, 2014; Koutsouleris et al., 2014; Liem et al., 2017; Luders, Cherbuin, & Gaser, 2016; Steffener et al., 2016) and build a novel data‐driven approach that is applied to the multi‐scale brain hierarchical partition (Diez, Bonifazi, et al., 2015) and estimates ChA exclusively based on a combination of SC and FC biomarkers. We denote this as the brain connectome age (BCA). Therefore, in contrast to BPA, no morphological features are incorporated into BCA. Notably, and distinctly from previous studies mostly showing that the hippocampus and its connectivity is the central circuit for tracing the aging process, BCA identifies the key role of the fronto‐striato‐thalamic (FST) circuit as the main network biomarker correlating with aging. Finally, we discuss the general implications and applications of the described methodology to a broader umbrella of key biomedical problems.

2. MATERIAL AND METHODS

2.1. Participants

Participants were recruited in the vicinity of Leuven and Hasselt (Belgium) from the general population by advertisements on websites, announcements at meetings and provision of flyers at visits of organizations, and public gatherings (PI: Stephan Swinnen). A sample of N = 155 healthy volunteers (81 females) ranging in age from 10 to 80 years (mean age 44.4 years, SD 22.1 years) participated in the study. All participants were right‐handed, as verified by the Edinburgh Handedness Inventory. None of the participants had a history of ophthalmological, neurological, psychiatric, or cardiovascular diseases potentially influencing imaging or clinical measures. Informed consent was obtained before testing. The study was approved by the local ethics committee for biomedical research, and was performed in accordance with the Declaration of Helsinki.

2.2. Imaging acquisition

Magnetic resonance imaging (MRI) scanning was performed on a Siemens 3T MAGNETOM Trio MRI scanner with a 12‐channel matrix head coil.

2.2.1. Anatomical data

A high‐resolution T1 image was acquired with a 3D magnetization prepared rapid acquisition gradient echo (MPRAGE): repetition time (TR) = 2,300 ms, echo time (TE) = 2.98 ms, voxel size = 1 × 1 × 1.1 mm³, slice thickness = 1.1 mm, field of view (FOV) = 256 × 240 mm², 160 contiguous sagittal slices covering the entire brain and brainstem.

2.2.2. Diffusion tensor imaging

A DTI SE‐EPI (diffusion weighted single shot spin‐echo echo‐planar imaging [EPI]) sequence was acquired with the following parameters: TR = 8,000 ms, TE = 91 ms, voxel size = 2.2 × 2.2 × 2.2 mm³, slice thickness = 2.2 mm, FOV = 212 × 212 mm², 60 contiguous sagittal slices covering the entire brain and brainstem. A diffusion gradient was applied along 64 noncollinear directions with a b value of 1,000 s/mm². Additionally, one set of images was acquired without diffusion weighting (b = 0 s/mm²).

Resting state functional data was acquired with a gradient EPI sequence over a 10 min session using the following parameters: 200 whole‐brain volumes with TR/TE = 3,000/30 ms, flip angle = 90°, inter‐slice gap = 0.28 mm, voxel size = 2.5 × 3 × 2.5 mm³, 80 × 80 matrix, slice thickness = 2.8 mm, 50 oblique axial slices, interleaved in descending order.

2.3. Imaging preprocessing

2.3.1. Diffusion tensor imaging

We applied DTI preprocessing similar to previous work (Alonso‐Montes et al., 2015; Amor et al., 2015; Diez, Bonifazi, et al., 2015; Diez et al., 2017; Kroos et al., 2017; Marinazzo et al., 2014; Rasero, Pellicoro, et al. 2017; Rasero, Alonso‐Montes, et al. 2017; Stramaglia et al., 2017) using FSL (FMRIB Software Library v5.0) and the Diffusion Toolkit. First, an eddy current correction was applied to overcome the artifacts produced by variation in the direction of the gradient fields of the MR scanner, together with the artifacts produced by head motion. To ensure that correlations with age were not due to differences in head motion (i.e., to correct for the effect that older people move more), the average motion of each participant was used as a covariate of noninterest in the statistical analyses. In particular, the participant's head motion was extracted from the transformation applied at the step of eddy current correction. The motion information was also used to correct the gradient directions prior to the tensor estimation. Next, using the corrected data, a local fitting of the diffusion tensor per voxel was obtained using the dtifit tool incorporated in FSL. Next, a fiber assignment by continuous tracking algorithm was applied (Mori, Crain, Chacko, & van Zijl, 1999). We then computed the transformation from the Montreal Neurological Institute (MNI) space to the individual‐participant diffusion space and projected a high‐resolution functional partition to the latter, composed of 2,514 regions and generated after applying spatially constrained clustering to the functional data (Craddock, James, Holtzheimer, Xiaoping, & Mayberg, 2012). This is an unsupervised clustering method, that is, after providing the 2,514 regions as an input (the clusters) that spatially constrains the different voxels belonging to the same region to be spatially contiguous. The best solution is the one that maximizes both within‐region similarity and between‐region difference.

Following this procedure we built 2,514 × 2,514 SC matrices, each per participant, by counting the number of white matter streamlines connecting all region pairs within the entire 2,514 regions data set. Thus, the element matrix (i,j) of SC is given by the streamlines number between regions i and j. SC is a symmetric matrix, where connectivity from i to j is equal to that from j to i. Exclusion criteria was based on not having the average head motion higher than the mean + 2 SD. None of the participants were excluded based on this constraint.

2.3.2. Functional MRI

We applied resting fMRI preprocessing similar to previous work (Alonso‐Montes et al., 2015; Amor et al., 2015; Diez, Erramuzpe, et al., 2015; Diez, Bonifazi, et al., 2015; Diez et al., 2017; Mäki‐Marttunen, Diez, Cortes, Chialvo, & Villarreal, 2013; Marinazzo et al., 2014; Rasero, Pellicoro, et al., 2017; Stramaglia et al., 2016, 2017; Stramaglia, Angelini, Cortes, & Marinazzo, 2015) using FSL and AFNI (http://afni.nimh.nih.gov/afni/). First, slice‐time correction was applied to the fMRI data set. Next, each volume was aligned to the middle volume to correct for head motion artifacts. After intensity normalization, we regressed out the motion time courses, the average cerebrospinal fluid (CSF) signal and the average white matter signal. Next, a band pass filter was applied between 0.01 and 0.08 Hz (Cordes et al., 2001). Next, the preprocessed functional data was spatially normalized to the MNI152 brain template, with a voxel size of 3 × 3 × 3 mm³. Next, all voxels were spatially smoothed with a 6 mm full width at half maximum isotropic Gaussian kernel. Finally, in addition to head motion correction, we performed scrubbing, by which time points with frame‐wise displacement >0.5 were interpolated by a cubic spline (Yan et al., 2013). We further removed the effect of head motion using the global frame displacement as a noninterest covariate, as old participants moved more than the young (when representing the mean frame‐wise displacement as a function of age provided a correlation value equal to 0.51 with a p value = 1E‐11), and this fact introduced nuisance correlations with age.

Finally, FC matrices were calculated by obtaining the pairwise Pearson correlation coefficient between the resting fMRI time series. Exclusion criteria was based on not having more than 20% of the time points with a frame‐wise displacement >0.5. Two participants were finally excluded.

2.4. Brain hierarchical atlas

The brain was divided in 2,514 brain regions that we grouped into modules using the brain hierarchical atlas (BHA), recently developed (Diez, Bonifazi, et al., 2015) and applied by the authors in a traumatic brain injury study (Diez et al., 2017). The BHA is available to download at http://www.nitrc.org/projects/biocr_hcatlas/. A new Python version, that was developed during Brainhack Global 2017—Bilbao, can be download at https://github.com/compneurobilbao/bha.

The use of the BHA guarantees three conditions simultaneously: (1) that the dynamics of voxels belonging to the same module is very similar, (2) that those voxels belonging to the same module are structurally wired by white matter streamlines; see in Figure 1 the high correspondence between SC and FC modules, and (3) when varying the level of the hierarchical tree, it provides a multi‐scale brain partition, where the highest dendrogram level M = 1 correspond to all 2,514 regions belonging to a single module (coincident with the entire brain), whereas the lowest level M = 2,514 correspond to 2,514 isolated modules (all of them composed of only one region).

Figure 1.

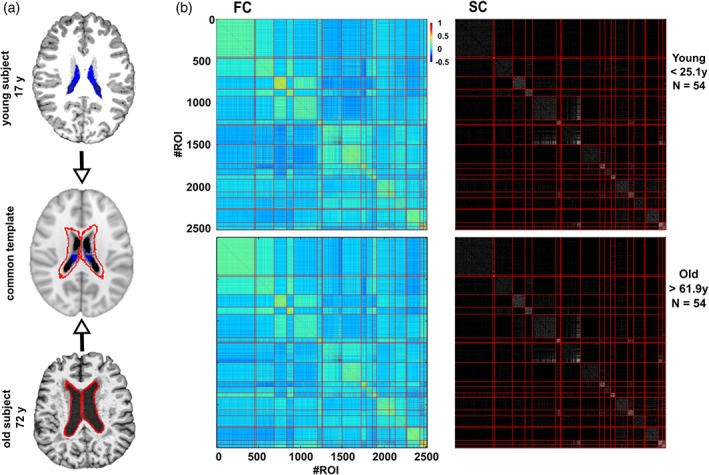
Robustness of the brain hierarchical atlas along lifespan. (a) Common template normalization (middle) for young (top) and old brains (bottom). Ventricle 3D segmentation has been performed for a young (17 years, filled in blue) and old participant (72 years, contours marked in red). Both segmentations are superimposed onto the common population template (middle row). For the connectivity analysis, regions located within the volume defined by the biggest ventricle size across all the participants have been ignored to correct for trivial age‐effects in the results of age estimation (i.e., to correct for the effect that older people have bigger ventricle volume). (b) Brain hierarchical atlas (BHA) parcellation for young (top) and old (bottom) populations shows the strong correspondence between functional modules (depicted as yellow squares in the matrix diagonal of the functional connectivity matrix, FC) and structural modules (plotted in the SC matrix). FC and SC matrices are the result of averaging FC and SC individual matrices in two different populations, young (age < 25.1 years, N = 54 participants) and old (age > 61.9 years, N = 54 participants). Both connectivity FC and SC matrices have been reordered according to the BHA (here represented at the level of M = 20 modules). FC is defined by the pairwise Pearson correlation between rs‐fMRI time series while SC is defined by the streamline counting between region pairs (here binarized just for illustration purposes) [Color figure can be viewed at http://wileyonlinelibrary.com]

It was also shown in Diez, Bonifazi, et al. (2015), that the hierarchical brain partition with M = 20 modules was optimal based on the cross‐modularity X, an index defined as the geometric mean between the modularity of the structural partition, the modularity of the functional partition, and the mean Sorensen similarity between modules existing in the two structural and functional partitions.

2.5. Multi‐scale structure–function correlo‐dendrograms of brain aging

From both SC and FC matrices, we built the correlo‐dendrogram (CDG) of brain aging by correlating ChA with the values of internal (intra‐module) and external (inter‐module) connectivity at each dendrogram level M of the BHA, and, by tuning the parameter M, we performed a multi‐scale connectivity analysis (Supporting Information Figure S1). For each module and participant, four different classes of features were built: functional internal connectivity (FIC), functional external connectivity (FEC), structural internal connectivity (SIC), and structural external connectivity (SEC; Figure 2). Given a brain module composed by a set of R regions, its associated FIC (SIC) was calculated as the sum of the functional (structural) weights of all the links between the elements of R, while FEC (SEC) was defined as the sum of the functional (structural) weights of all the links connecting the elements of R to other regions in the brain.

Figure 2.

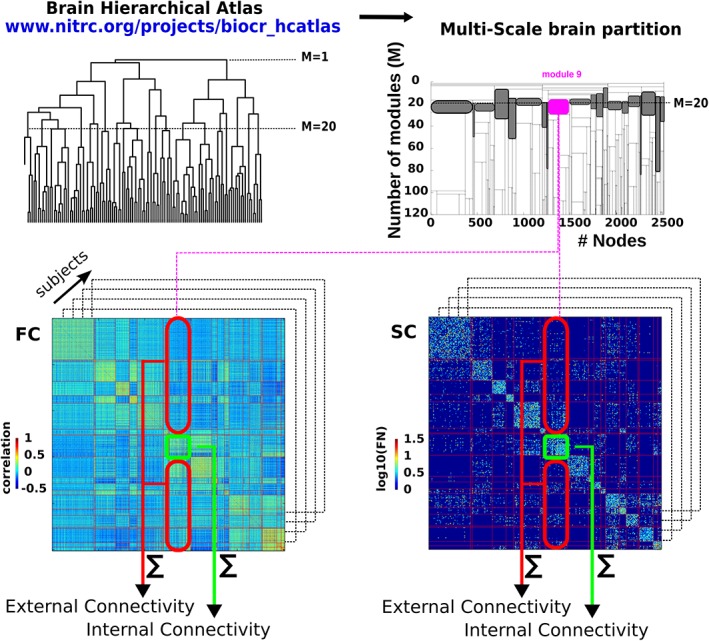
Schematic representation of the structure–function multi‐scale approach. Left‐top: First, we have made use of BHA to define different modules resulting from a hierarchical agglomerative clustering. Right‐top: The multi‐scale brain partition shows how modules divide when going down along the tree (here, we only depict a subpart of the tree that goes from 20 to 120 modules). The gray‐colored modules represents the M = 20 brain partition. Bottom: For the tree level of M = 20 and for each participant, we calculated the structural/functional internal connectivity (green rectangle) and structural/functional external connectivity (red rectangle), by summing, respectively, the edge weights within and leaving out that module. The approach becomes multi‐scale when applying the same procedure to all the modules across all the 20 ≤ M ≤ = 1,000 levels of the hierarchical tree. Shaded boxes represent the modules present at the partition level M = 20. Note that the modules are differentially present in previous and following partitions. Thus, the number of partition levels in which a given module is present, represents a stability measure of that module in the tree division [Color figure can be viewed at http://wileyonlinelibrary.com]

One of the properties of the BHA is that at each M level only one of the branches of the hierarchical tree divides in two, and therefore only two modules at each level are new with respect to the (M − 1) upper levels (Figure 2). Taking into consideration this point together with the fact that we started our analysis at the level of M = 20 and arrived up to M = 1,000, we established the Bonferroni significance threshold equal to 0.05/[20 + 2 × (1000 − 20)] for the correlation between age and connectome metrics (FIC, SIC, FEC, SEC). While the BHA comprises 2,514 ROIs the final level of M = 1,000 was chosen to compromise between the possibility to reach a very high spatial resolution (in average, each of the modules at the partition level M = 1,000 contain 48 voxels) while limiting the impact of the Bonferroni correction for multiple comparisons on the detection of significant features.

To localize age‐affected brain areas at both functional and structural levels (rather than separate FC or SC analyses), and thus obtaining a major benefit from the combination of functional and structural data, we searched for brain regions such that their p values were determined by the square root of the product of the SC p value multiplied by the FC p value, and chose the ones that survived after Bonferroni correction. Consequently, the value of the structure–function age correlation was calculated as the geometric mean of the two correlation values, one achieved by the functional feature and the other by the structural one.

2.6. Brain connectome age

To estimate age, we performed a multi‐scale methodology obtained from the structure–function connectome. We first defined for each participant n the vector $x^n\equiv {\left(1x_1^n{x}_2^n\mathrm{\cdots }{x}_{K-1}^n\right)}^T$ of K components, each one corresponding to one connectivity feature previously obtained by the structure–function CDGs, and where T denotes the transpose operator. The estimated age for the participant n was calculated by a linear combination of the features, that is,

$$t_n={\omega }_0+{\sum }_{j=1}^{K-1}{\omega }_j{x}_j^n+{\varepsilon }_n,$$ (1)

where ɛ_n is a zero mean Gaussian random variable with variance σ², and ω ≡ (ω₀ω₁ω₂⋯ω_K − 1)^T is the weight vector. For P different participants, using Equation (1), we defined the error function as

$$E\left(\omega \right)=\frac{1}{2}{\sum }_{n=1}^P{\left\{t_n-{\omega }_0-{\sum }_{j=1}^{K-1}{\omega }_j{x}_j^n\right\}}^2,$$ (2)

which allows to calculate the weight vector ω that minimizes the error function (i.e., which is solution of the first derivative of E(ω) with respect to ω equal to zero). Such a minimum defines the maximum likelihood estimator (MLE), which can be analytically solved (Bishop, 2006; Cortes, Lopez, Molina, & Katsaggelos, 2012) and is given by:

$$w^{\mathrm{MLE}}={\left({\varphi }^T\varphi \right)}^{-1}{\varphi }^{T}t$$ (3)

where the exponent −1 denotes the inverse of the matrix, t ≡ (t₁t₂t₃⋯t_P)^T the vector of P different estimations and ϕ the so‐called design matrix, that is,

$$\varphi \equiv \left(\begin{array}{c}1x_1^1{x}_2^1\mathrm{\cdots }{x}_{K-1}^1\\ 1x_1^2{x}_2^2\mathrm{\cdots }{x}_{K-1}^2\\ \mathrm{⋮}\\ 1x_1^P{x}_2^P\mathrm{\cdots }{x}_{K-1}^P\end{array}\right).$$ (4)

When the entire data set is used to calculate w^MLE, the estimation error decreases when the number of features increase (that is, the more features we add into the model, the better the estimation), but this strategy also provides a very high variance estimate, meaning that, when estimating the age using MLE in a different data set can produce a very high error. Splitting the entire data in training and testing sets can solve this problem, also known as overfitting (James, Witten, Hastie, & Tibshirani, 2013). Therefore, to calculate the mean absolute error (MAE), for each cross‐validated experiment we performed data splitting, by randomly choosing 75% of the data set (N ₁ = 115) for training (i.e., for calculating the w^MLEsolution) and the remaining 25% (N ₂ = 38) for testing (i.e., to calculate the MAE) within each cross‐validated experiment.

As a metric for the estimation quality, the MAE was calculated on the test data for each cross‐validated experiment using

$$\mathrm{MAE}\left(K\right)=\frac{1}{N_2}{\sum }_{n=1}^{N_2}\left|{\mathrm{ChA}}_n-{\mathrm{BCA}}_n\left(K\right)\right|,$$ (5)

where |.| denotes absolute error and where we defined the BCA for participant n as

$${\mathrm{BCA}}_n\left(K\right)\equiv {\omega }_0^{\mathrm{MLE}}+{\sum }_{j=1}^{K-1}{\omega }_j^{\mathrm{MLE}}{x}_j^n,$$ (6)

where w^MLE is defined in Equations (3) and (4).

Remark that although in principle there were many potential features (four classes—FIC, FEC, SIC, and SEC—per module and number of modules M varying from 20 to 1,000), finally only K of them were introduced into the MLE to estimate age. Therefore, and by construction, the MLE solution depends on K (see next subsection for the choice for the K features). A diagram for the BCA method is also shown in Supporting Information Figure S2.

2.7. Optimization of the MLE

To get the optimal model, that is, the K features that better estimate age, we followed this procedure:

1. For K = 1, we considered the feature that best correlated with ChA.

2. The K = 2 feature was chosen among all the remaining ones by finding the feature such that after U = 100 experiments of randomly choosing 75% of the data set for training and 25% for testing, the mean MAE achieved by the two features (the one found in stage 1 plus the new one) was minimal.

3. The K = 3 feature was chosen among all the remaining ones by finding the feature such that after U = 100 experiments of randomly choosing 75% of the data set for training and 25% for testing, the mean MAE calculated with three features (the previous two features found in stage 2 plus the new one) was minimal.

4. Following this strategy, the curve MAE(K) had a minimum value as K increases, that defined the optimal model which has K features.

2.8. Adding nonlinearities to the age estimation

Although Equation (1) accounts for a linear dependence on connectivity features, the MLE strategy is more general and allows to incorporate different classes of nonlinearities, such as quadratic or higher‐order polynomial terms, or other functions such as, for instance, Gaussian, Exponential or Sigmoid, just by adding new columns accounting for such dependencies into the design matrix given by Equation (4) (for further details see (Bishop, 2006). In this work, we study linear and quadratic contributions into the MLE estimation.

2.9. Labelling of anatomical regions

The anatomical identification for each of the 2,514 brain regions has been performed using the automated anatomical labeling (AAL; Tzourio‐Mazoyer et al., 2002) brain atlas, and as a consequence, the anatomical labels used in this work follow the ones existing in the AAL atlas.

2.10. Removal of regions affected by the increment of ventricular space along lifespan

Ventricular space increases along the lifespan in a manner that, after transforming all images to a common space, some regions surrounding the ventricular space for the younger population are occupied by the ventricular space of older participants. To remove this effect, that introduces a strong bias in the age estimation, we deleted these regions by (after projecting all images to the common space) searching for the participant with the highest ventricular volume, segmenting this space and treating it as mask to discard (for the connectivity analysis) all the regions within this space in all the participants. Figure 1a illustrates this procedure.

2.11. An alternative method based on probabilistic tractography to calculate SC matrices

Probabilistic tractography was calculated using FSL. We first estimated a probabilistic model to compute fiber orientation using bedpost (paper: https://www.ncbi.nlm.nih.gov/pubmed/17070705). Second, we calculated connectivity matrices (one per subject) using probtrackx2 and 100 pathways per voxel. Connectivity matrices were calculated without introducing any threshold at the probability to define a connection, and therefore, connectivity features were obtained summing in a weighted manner over all connection probabilities that each modules has to the rest of the brain or within itself.

3. RESULTS

A population of N = 155 healthy participants (81 female, 74 male) with age varying from 10 to 80 years (mean = 44, SD = 22) was used for the study. Triple acquisitions including structural, diffusion tensor, and resting functional imaging were acquired for each participant.

We used the multi‐scale BHA with 2,514 regions and calculated for each participant the SC and FC connectivity matrices, representing, respectively, the pairwise region streamline number and the pairwise Pearson correlation coefficient between the resting fMRI time series.

We first validated the use of BHA for the study of aging by showing a high correspondence between the modules in SC and those in FC independently on participant age. In particular, Figure 1 illustrates for two populations, one young (age < 25.1 years, N = 54 participants) and other old (age > 61.9 years, N = 54 participants), the correspondence between SC and FC by assessing cross‐modularity (X) (Diez, Bonifazi, et al., 2015), obtaining X = 0.312 for the young population and X = 0.309 for the old, and therefore showing that cross‐modularity was 99% preserved along the lifespan. Of note, the two values of cross‐modularity (young and old) are similar to the ones obtained in two different data sets, one acquired in our Hospital and from the Human Connectome Project, cf. Supporting Information Figure S8 in Diez, Bonifazi, et al., (2015), providing robustness across different data sets.

Next, to possibly achieve the best spatial resolution while limiting the strict constraints due to the statistical assessment of very large number of features (multiple‐comparison problem), we calculated for increased levels M of the BHA (with 20 ≤ M ≤ 1,000), four different module features (Figure 2): (1) the FIC, (2) the FEC, (3) the SIC, and (4) the SEC. This approach allowed us to build a CDGs (correlation between age and each module connectivity within the dendrogram) to find the highest correlation between module connectivity and ChA, while maximizing the spatial resolution in a multi‐scale manner. The structure–function CDG was next obtained as the geometric mean between the correlations achieved from the structural and functional CDG separately. Figure 3 illustrates the maximum of the age correlation across the multi‐scale partition, for external module connectivity features (Figure 3a), for internal module connectivity (Figure 3b) and for three classes of connectivity features: linear (left column), quadratic (middle column), and only quadratic (right column), the latter obtained as the brain maps difference between the quadratic case and the linear one.

Figure 3.

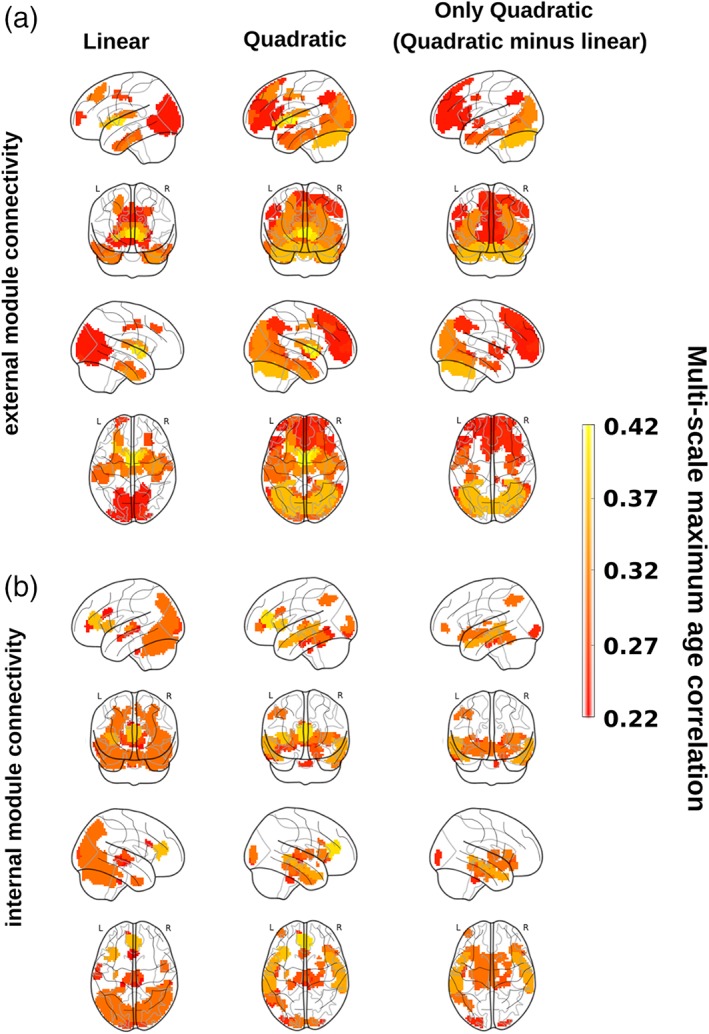
Structure–function correlo‐dendrograms (CDGs) and brain maps of maximum age correlation across all levels of the multi‐scale brain partition. To build structure–function CDGs, we calculated for each module appearing in the BHA partition (20 ≤ M ≤ 1,000) the correlation (and associated p value) between age participant and FEC, FIC, SEC, and SIC and assessed the structure–function module connectivity as the geometric mean of the two correlation values, one achieved by the functional feature and the other by the structural one. By varying the level M in the multi‐scale brain partition, brain maps were obtained by plotting the maximum value of correlation across all M levels in the CDG (that we have defined as the multi‐scale maximum age correlation). Brain maps are obtained by separating the analyses of external (panel a) and internal (panel b) module connectivity after linear (left column) and quadratic (middle column) fits. For illustration purposes, we also plot the difference between the two brain maps, quadratic minus linear (right column). All the nonzero correlation values plotted here are statistically significant after Bonferroni correction [Color figure can be viewed at http://wileyonlinelibrary.com]

3.1. Brain areas correlating with age in relation to external connectivity

Figure 3a shows the results of the maximum age correlations across multi‐scale partitions obtained for the external connectivity analysis (i.e., inter‐module connectivity therefore generally associated to longer fiber connections). Significant linear connectivity features (left column) were found bilaterally in several cortical and subcortical AAL regions: frontal superior and middle, cingulum middle, parahippocampus, calcarine, cuneus, lingual, occipital superior, middle and inferior, fusiform, precuneus, caudate, putamen, thalamus, temporal pole middle, and temporal inferior. When looking at the quadratic features (middle column), the most striking difference was represented by the presence of the prefrontal and occipital cortices, not observed when only linear terms were taken into account and highlighted in the brain maps of the significant quadratic‐but‐not‐linear features (right column).

3.2. Brain areas correlating with age in relation to internal connectivity

Figure 3b shows the results of the maximum age correlations across the multi‐scale partition obtained for the internal connectivity analysis (i.e., intra‐module connectivity and generally associated to shorter fiber connections). Significant linear connectivity features were found bilaterally in the insula, cingulum anterior, calcarine, cuneus, occipital superior, middle and inferior, fusiform, parietal superior, angular, precuneus, thalamus, temporal middle and inferior, and cerebellum. When looking at the quadratic features (middle column), the most relevant result was the presence of the memory (hippocampus and temporal pole) and limbic (amygdala) circuits, which was not observed when only linear terms where considered into the model (right column).

3.3. Network homeostasis

As the structure–function CDG does not provide any information on the individual contribution that either the structural or the functional feature has on the correlation value, by looking at the linear model we separated the four possible cases of combined correlations (increased structural and functional; decreased structural and functional; increased structural and decreased functional; decreased structural and increased functional) and reported them separately in Figure 4.

Figure 4.

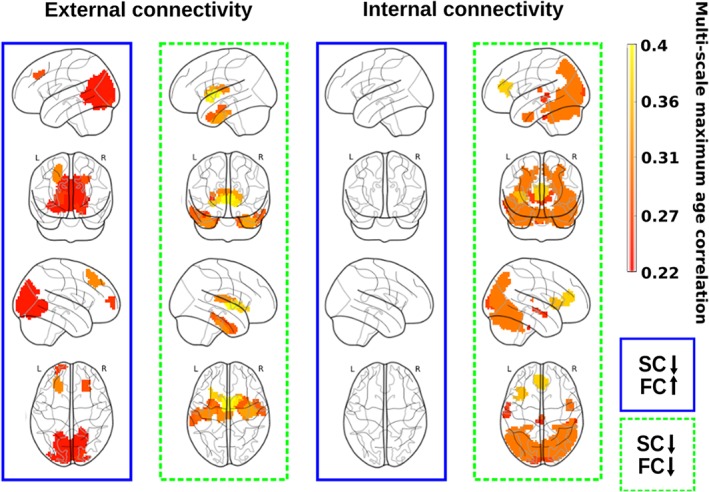
Functional connectivity modulation by variations in the structural connectivity along lifespan. SC decreases with age, but FC might either increase (blue rectangle) or decrease (green rectangle), and the latter only occur when looking to external connectivity patterns (left column). Indeed, when looking to internal connectivity patterns (right column), the situation of SC decreasing and FC increasing did not exist (transparent brains), and the connectivity patterns only reflect both SC and FC decreasing with age (green rectangle) [Color figure can be viewed at http://wileyonlinelibrary.com]

The external connectivity analysis (Figure 4, left column) identified brain regions with opposing tendencies, that is, regions where the SC decreased with age while the FC increased (blue rectangle), a mechanism representing network homeostasis. These regions were found bilaterally in the frontal superior and middle, calcarine, cuneus, lingual, occipital superior, middle and inferior, and precuneus. Regions for which both structural and functional connectivities decreased with age (green rectangle) were found bilaterally in the parahippocampus, fusiform, caudate, putamen, thalamus, and temporal pole middle and inferior.

The internal connectivity analysis (Figure 4, right column) did not identify any brain region in which the SC decreased with age and the functional one increased (blue rectangle), indicating that network homeostasis only was appreciated when looking to external connectivity patterns. Regions where both structural and FC decreased with age (green rectangle) were found in the insula, cingulum anterior (the anterior part of the default mode network), calcarine, cuneus, occipital superior, middle and inferior, fusiform, parietal superior, angular, precuneus, temporal middle and inferior, and the cerebellum.

3.4. Brain connectome age

To calculate the BCA from MLE (see Section 2) we used the 50 most correlated (in absolute value) connectivity features for each of the four cases (FIC, FEC, SIC, SEC) that provided a considerable number of Q = 200 possible features (Supporting Information Figure S2). As explained in Section 2, we used 75% of the data set for training (to calculate the MLE solution) and the remaining 25% for testing (to calculate the MAE). Starting from the most correlated feature and adding one by one features optimizing the age estimation (see Section 2), the linear model provided the optimal age estimation at K = 38 features (Figure 5a), corresponding to a minimum mean MAE value (after U = 100 repetition experiments) equal to 5.89 years. A full list of the K = 38 optimal features is provided in Supporting Information Table S1. When calculating MLE using these K = 38 best features, the graphical representation of ChA as a function of BCA showed an excellent correspondence (Figure 5b, correlation = .95, p value < 10⁻²⁰, results corresponding to one of the U = 100 experiments chosen because its MAE value was the most similar to the average MAE between all the U = 100 experiments). In terms of age prediction performance, the quadratic model did not perform better than the linear case (the minimum MAE was equal to 6.16 years and was achieved at K = 32 features).

Figure 5.

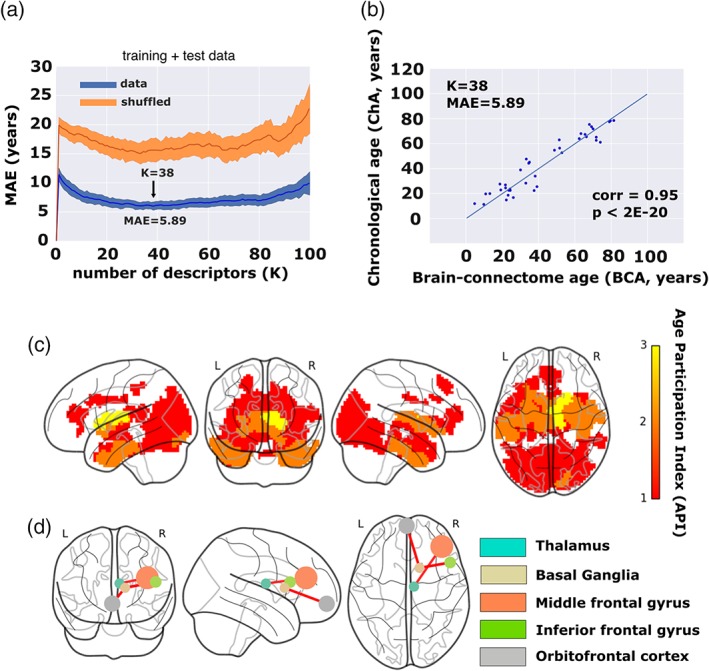
Chronological age (ChA) versus brain connectome age (BCA). (a) Correlation between ChA and BCA as a function of the number of features (K). The minimum MAE corresponds to 5.89 years, achieved when K = 38 different features have been incorporated into the maximum likelihood estimator. In blue, we color results from real data, and in orange, results after shuffling the age vector a number of U = 100 experiments, which provides the null‐distribution (here represented the mean ± SD). (b) For one of the U = 100 experiments (chosen because its corresponding MAE was the most similar to the average MAE along the U = 100 experiments), we plot ChA (in years) as a function of the BCA (here, equal to the MLE solution with the best K = 38 best connectivity features), which provides a correlation value of 0.95 (p < 2E‐20). (c) Brain maps of the K = 38 best features. Color bar indicates age participation index (API), accounting for how many times one brain region is significantly correlated with age in relation to any of the four following categories: SEC, SIC, FEC, and FIC. Basal ganglia and thalamus are the brain structures whose connectivity participates most prominently in aging. (d) Basal ganglia and thalamus connect according to a structure–function manner to the inferior and middle frontal gyri together with the orbitofrontal cortex, that is, the so‐called fronto‐striatothalamic (FST). Therefore, the FST is the major circuit participating in brain aging. Node size is proportional to the volume size of the region that participates in this network, whereas link thickness is proportional to structure–function correlation values [Color figure can be viewed at http://wileyonlinelibrary.com]

3.5. Age participation index

The brain maps corresponding to the best K = 38 features are shown in Figure 5c. Because by model construction each of the 2,514 regions might participate in four classes of features (FIC, FEC, SIC, SEC), we calculated for each region its age participation index (API), that is, an integer number between 0 and 4 indicating with how many of the four classes a specific brain region contributed to the age estimator model. Regions with API = 1 were found bilaterally in the frontal superior, insula, cingulum anterior and middle, hippocampus, parahippocampus, calcarine, cuneus, lingual, occipital superior, middle and inferior, fusiform, precuneus, thalamus, temporal middle and inferior, and temporal pole middle. Regions with API = 2 were found bilaterally in the parahippocampus, fusiform, caudate, putamen, thalamus, temporal pole middle, and temporal inferior. Finally, regions with API = 3, and therefore, the regions with a major correlate of physiological aging were found in the connectivity of basal ganglia (BG; caudate, putamen, pallidum) and thalamus. Although by construction was possible, no regions existed with API = 4.

3.6. Structure–function connectomics reveals that the FST pathway is the major circuit for age estimation

Finally, we looked into what brain areas were connected to those regions with API = 3. Functionally, we found bilateral connections to orbitofrontal (superior, middle, and inferior), middle frontal, olfactory, gyrus rectus, cingulum (anterior, middle, and posterior), calcarine, middle occipital, fusiform, precuneus, temporal middle, and cerebellum. Structurally, regions with API = 3 were interconnected between them and also connected with the insula. Finally, regions with API = 3 (including caudate, putamen, pallidum, and thalamus) had structure–function interconnections between them and also were connected to the orbitofrontal and frontal cortices (Figure 5d).

4. DISCUSSION

The ChA differs from the biological one. While the former is defined as the time running as birth, the latter quantifies the maturity level that an individual (or an organ) has at the operational level. In relation with the brain, the discrepancy between the brain age and ChA might work as a biomarker for quantifying deterioration as a result of disease or improvement after some treatment or therapy, which has unlimited applications. Here, we asked whether the brain age could be determined exclusively based on structure–function connectivity metrics, and therefore, we did not take into consideration typical morphological characteristics, such as gray and white matter atrophy or ventricular volume, that have been widely shown to correlate with ChA. Our results demonstrate that the BCA is an accurate estimation of ChA, and provides a MAE of 5.89 years in a group of N = 155 participants with age ranging from 10 to 80 years. Our results also reveal that the BG/thalamus and their connection with frontal areas is the key circuit accounting for the age estimation.

4.1. Differences between brain age and ChA by assessing brain morphology

Several studies have assessed discrepancies between brain morphological age and ChA for measuring brain functioning in pathological groups. In relation with MCI, it was shown that the brain age could become even 10 years higher than ChA (Franke et al., 2010). In a different study, it was shown that the error in age estimation predicted the conversion from MCI to Alzheimer's disease better than any other variable (Gaser et al., 2013), as compared to imaging morphological variables (such as the volume of subcortical structures), cognitive scales or protein biomarkers in CSF. One‐year bias was associated to 10% higher risk conversion. In relation to other pathologies, and also using morphological features to estimate the brain age, the difference between brain age and ChA explained for instance brain deterioration from attenuated psychosis to chronic schizophrenia (Koutsouleris et al., 2014), brain deterioration in patients with human immunodeficiency virus (Cole, Underwood, et al., 2017), accelerated atrophy after traumatic brain injury (Cole et al., 2015; suggesting that the chronic effects after the insult can resemble normal aging), but also brain rejuvenation after meditation (Luders et al., 2016).

Morphological age‐related alterations have been reported in all body organs, such as liver, kidney, heart, lung, skin, but notably, what makes the brain distinct from other organs is precisely its complex wiring, where short‐range connectivity operates at multiple scales in combination with long range circuitry, allowing the two main brain functional principles of segregation and integration (Tononi, Sporns, & Edelman, 1994) to work in harmony. Therefore, the BCA model presented here provides a new complementary and fundamental approach within the above framework, fully focused on the multi‐scale organization of the brain circuitries and networks, enabling to correlate aging with lower and higher brain functions.

4.2. Differences between brain age and ChA by assessing brain connectivity: Importance of combining SC and FC in a multi‐scale approach

Only very few studies have made use of connectivity metrics for age estimation, but none so far have combined in a multi‐scale manner SC and FC metrics to perform the estimation. By combining morphological features together with FC ones, the error in the age estimation was shown to be 4.29 years (Liem et al., 2017). In relation to connectivity metrics, a seminal study showed that resting FC features estimated brain age (Dosenbach et al., 2010), but rather than addressing physiological aging, the authors focused on neural development in the age range between 7 and 30 years. Using only structural networks, but not functional data, it was shown that a simple metrics such as the sum of all connectivity links (i.e., streamline number) weighted by the age‐link correlation, estimated ChA with high precision (Han et al., 2014) in healthy participants aged 4–85 years.

Here, by combining both SC and FC features in a multi‐scale manner, we have achieved a high performance, quantified by an accuracy of 5.89 years. To the best of our knowledge, such an approach has never been reported before in the context of age estimation. When repeating the entire procedure using only SC features, the performance was worse (accuracy of 8.1 years). Analogously, when using only FC features, the performance was also worse (accuracy of 8.45 years).

Our results not only reveal the relation between BCA and the aging process, but also highlight how the wiring and the dynamics of brain networks cannot be disentangled without losing the emergent synergetic picture for their operational complexity. Indeed, when looking solely at function, as it occurs in task‐fMRI, a distinct scenario emerges, the so‐called frontal super‐activation, where younger people exhibit no or lateralized frontal activation when performing the task, while older people incorporate unilateral or bilateral frontal cortex activation (Cabeza, 2002). Our BCA model, although obtained when the brain is at rest, extends task‐related studies, revealing that the fronto‐subcortical (striatum and thalamus) complex is the primary circuit critically accounting for the functional age‐deterioration. Indeed, the key element is that the multi‐scale BCA approach used in this work perfectly preserves the intrinsic link between structure and function. In fact, the resting activity is shaped by modular organization, where the structural and functional architecture clearly correspond each other (Diez, Bonifazi, et al., 2015).

4.3. Structure–function connectivity between subcortical areas (striatum and thalamus) and frontal cortex is the principal circuit for brain aging

Our structure–function multi‐scale analysis has shown that the FST pathway is the major circuit for age estimation. Several studies have shown that the connectivity profile of the BG and thalamus is affected by aging and correlates with age‐related neuropsychological decay. For example, a reduction in thalamic volume along the lifespan has been associated with age‐related sensorimotor performance deterioration (Serbruyns et al., 2015). In relation to BG, and far beyond its classical association to motor function (Kandel, Schwartz, Jessell, Siegelbaum, & Hudspeth, 2012), there is nowadays mounting evidence to associate the BG decline with executive function deficits along the lifespan, such as motor switching (Coxon et al., 2010), inhibitory (Coxon et al., 2016; Leunissen, Coxon, & Swinnen, 2016), and cognitive control (Grady, 2012), but also learning (Chalavi et al., 2018), whereby older adults perform worse than young. The status of connectivity between the thalamus and BG, by means of the FST circuit, has been associated with task‐switching performance (Coxon, Van Impe, Wenderoth, & Swinnen, 2012; Leunissen et al., 2013, 2014a, 2014b), reflecting the capacity for suppression of certain actions to flexibly adopt new different ones. However, what makes our approach particularly novel (and without any a priori assumption about the participation of these regions) is that it provides quantitative evidence that the FST circuit makes the major contribution for age estimation.

Different studies have argued that aging and age‐associated cognitive impairment is dominantly mediated by the hippocampus (HIP) and this is supported by the overwhelming amount of work done on this brain area in human and animal systems during the past decades, see for instance (Bartsch & Wulff, 2015; Driscoll et al., 2003). Therefore, these studies support the general idea that healthy aging in somehow related (likely in a less aggressive manner) to neurodegenerative aging, where the disruption of the HIP circuit has been clearly established (Andersen, 2007). Although our analysis has shown that HIP has an API of 1 (and therefore finds some role in aging), however, we have demonstrated that the medial subcortical–cortical FST pathway is the major circuit‐mediating aging (with an API three times higher than the one for HIP).

Aging appears to affect the FST circuit more profoundly than the HIP. This emerges from the list of K = 38 optimal connectivity features for the BCA (Supporting Information Table S1). In total, there are 10 features belonging to the FST circuit and 4 features belonging to the HIP circuit. Within the 10‐FST and the 4‐HIP features, the maximum correlation with age is −0.72 for FST and − 0.46 for HIP (Supporting Information Figure S4). Therefore, both circuits participate in aging, but FST dominates in the participation.

We infer from these results that future research on brain aging should make an increasing effort to study the FST circuit in much more detail, thereby differentiating different classes of aging: healthy (FST‐mediated) versus Alzheimer's‐dementia (hippocampus‐mediated).

4.4. Network homeostasis: Increased FC in combination with decreased SC

Increased FC in the pathological brain has been observed before in different studies on traumatic brain injury (Diez et al., 2017) or Alzheimer's Disease (Diez, Erramuzpe, et al., 2015). It is however not possible to establish a direct association between increased FC and behavioral or cognitive improvements. Indeed, studies have shown that increased FC can be associated with behavioral improvement (Grady, 2012; Hernandez‐Castillo et al., 2017) but also with behavioral impairment (Diez, Erramuzpe, et al., 2015; Diez et al., 2017). Accordingly, in the circuits where functional homeostasis exists (i.e., increased FC together with decreased SC), the circuit's functionality might improve or deteriorate. Future research should look into this problem in further detail.

4.5. A general and novel methodology to quantify the multi‐scale structure–function brain connectivity impact of therapies, diseases, and lifestyles

The originality of our approach is based on identifying in multi‐scale manner brain modules whose connectivity correlate structurally and functionally with age. Next, the significant features are pooled to create an optimized linear regression model capable to assess the biological brain age of a given connectome with minimal error. Such a methodology opens two important and different perspectives. First, it provides a quantitative approach to assess the impact of therapies on biological brain aging (ideally rejuvenating the brain connectome), diseases (accelerating the connectome aging), and other factors shaping lifestyle. Second, the same methodology can be used to correlate any graded variable to the brain connectome, and not only age as approached here, thus allowing for brain connectome estimators of any other biomarker. In this framework, a biomarker might be any functional, structural, or behavioral score obtained from participants for instance, protein levels from CSF or blood, or a clinical scale measuring disease severity.

4.6. Methodological considerations

• The possibility of stratifying the problem of age estimation along different intervals of age. We have built a MLE and estimated age from the entire data set, but separating the data in small sets improved our results. When repeating the same procedure only to a young group (N ₁ = 50, 10.88 < age < 25), and after optimizing the BCA estimation, we achieved MAE = 1.21 using K = 28 connectivity features. Similarly, for a group of adults (N ₂ = 49, 25 < age < 60) and old participants (N ₃ = 56, 60 < age < 80.67) we achieved, respectively, MAE equal to 2.49 (K = 30) and 1.57 (K = 34), and therefore by stratifying the data set along different groups of age, the BCA estimated age more accurately. Notice that, although unstable BCA estimations could occur for small populations, this does not appear to apply to our study, as the ratios of MAE divided by the age range (maximum age minus minimum age) for the three main groups (N ₁ = 50 young population, age range 15 years; N ₂ = 49 medium age population, age range 35 years; N ₃ = 56 old population, age range 20 years) provide similar values (respectively, Z ₁ = 1.21/15 = 0.08, Z ₂ = 2.49/35 = 0.07, and Z ₃ = 1.57/20 = 0.08) to the entire population (Z = 5.89/70 = 0.08, N = 155 subjects).

• Comparison in performance to different models for age estimation. It is important to remark that the value of MAE of BCA equal to 5.89 years is no better than the performance of some other prediction models using merely volumetric data (Cole, Poudel, et al., 2017; Franke et al., 2010; Mwangi et al., 2015). However, the objective of our study is not only to maximize the model performance, but to show that we can estimate age as well using exclusively structure–function connectivity features as compared to morphological features. In other words, we show here that age affects the brain's morphology in a similar manner as its connectivity patterns. In addition, our method reveals that the FST circuit participates to the largest extent in age prediction. From the engineering point of view of maximizing the model performance, one should combine cognitive features (e.g., scores in neuropsychological tests or tasks) with MRI features (such as volumetric and connectivity features) to unveil the redundancy or synergy of information between connectivity, morphology, and neuropsychological features. Future studies are needed to address these questions.

• Differences between quadratic and linear features for age estimation. We have shown a slightly better performance using linear features in comparison to quadratic ones (MAE = 5.89 vs. MAE = 6.16). It has been shown that cognitive performance across different tasks often shows an inverted‐U shape pattern, that is, performance levels are low when young, improve during adulthood, and decrease again when getting older. Accordingly, to search for best features of such behavior, quadratic terms are likely to be more relevant. We hypothesize that, as the “response” (i.e., age) being predicted is linear, and not quadratic, linear features seem to work better. But, to really demonstrate that this is the case, more elaborate methods have to be developed.

• The possibility of extending the method to edge (rather than node) metrics for age estimation. Lastly, our method makes use of network node metrics to estimate brain age, but this method can also be extended to the link level, thus identifying specific pathways rather than brain regions, provided a large cohort is available to control for multiple comparisons (as a given connectome has N nodes and N ² links).

• Using SC matrices based on probabilistic tractography does not affect the result on the FST circuit. We have calculated SC matrices based on deterministic tractography, which assumes that only one tract orientation per voxel can exist. A different class of methods to calculate SC is probabilistic tractography, where using different seeds to track the fibers, the method estimates a probability value of water diffusion per voxel. With regard to external connectivity, probabilistic tractography matrices revealed maximum age correlation bilaterally at anterior and middle cingulum, parahippocampus, fusiform, caudate, putamen, pallidum, thalamus and temporal pole (Supporting Information Figure S3a). In comparison to deterministic tractography (Figure 3a, linear case), we observe overlap and similarity across several brain regions (such as the striatum, thalamus, temporal pole, fusiform, parahippocampus, and middle cingulum). However, we also find a lower number of areas correlating with age, possibly because deterministic tractography provides more sparse connectivity matrices with more true positives fibers. Similarly when looking at internal connectivity (Supporting Information Figure S3b), probabilistic tractography matrices revealed maximum age correlation bilaterally at the cingulum anterior, thalamus, middle temporal, and temporal pole (with several areas coinciding between probabilistic and deterministic tractography), and fewer areas in total correlating with age in comparison to deterministic tractography.

• Poor co‐registration for some distorted areas between diffusion and functional data. The susceptibility‐induced distortions are different between diffusion MRI and resting state fMRI images, especially in the brain stem and skull base regions. Therefore, it is still difficult and challenging to ensure that the partitioned regions (especially those near the severely distorted brain regions) are projected to the same anatomical locations in both diffusion and fMRI images, and no automatic pipelines currently exist to perform this task. In this work, similar to most of previous studies, we assume that current methods for co‐registration between fMRI and diffusion data achieved by the T1‐mediated subject‐to‐template transformation are still valid. Although this is beyond the scope of the present work, future work combining FC and SC should pay attention to this technical but important issue.

5. SUMMARY

We have shown that the ChA can be estimated with a much higher accuracy using structural–functional connectomics than separate structural or FC metrics. The strategy of assessing the mismatch between chronological and brain age is suggested to be useful for quantifying the brain's deterioration or its reorganization after new treatments, implying a multitude of meaningful applications. Using a blind approach in which no brain structures were a priori assumed to be affected by aging, our multi‐scale method has shown that the connectivity of the FST circuit is critically important for brain aging, consistent with previous work associating this circuit to age‐related deterioration of cognitive control of a multitude of actions.

Supporting information

Figure S1: From correlo‐dendrograms (CDGs) to brain maps. To build structure–function CDGs, we calculated for each module appearing in the BHA partition (20 < =M < =1,000) the correlation (and associated P‐value) between age participant and features (FEC, FIC, SEC and SIC) and we assessed the structure–function module connectivity as the geometric mean of the two correlation values (one achieved by the functional feature and the other by the structural one). By varying the level M in the multi‐scale brain partition, brain maps were obtained by plotting for each of the 2,514 regions, the value of maximum significant correlation across all M levels in the CDG (significance is based on the product of the structural and functional P‐values, see section 2). Brain maps are obtained by separating the analyses of external (panel a) and internal (panel b) module connectivity for linear (here illustrated) and quadratic (see Figure 3) correlations. a: Within the multi‐scale brain partition graph (representing the partition level, that is, number of modules, versus the brain nodes; similar to what shown in Figure 2 top right panel but without delimiting the modules with lines to allow a best visualization) modules displaying a significant structural–functional external connectivity correlating with age are color‐coded (the top inset show a zoom on a few modules displaying significant correlations). Brain maps showing the maximal correlation with age are shown in the bottom. b: same as panel a but for internal connectivity.

Figure S2: Diagram for Brain Connectivity Age (BCA). The BCA method uses CGD (Figure S1) as a preprocessing step to provide a pool of “Q multi‐scale features with significant correlation with age.” The core of the BCA method is the “optimization algorithm” (detailed in the inset panel at the right and fully developed in the text), which provides the “optimal features” before performing the age estimation exclusively based on structure–function connectivity features (BCA). Here, we used Q = 200. Abbreviations used in the diagram: NposF = Number of possible Features; posF = possible Feature; NmodF = Number of model Features; modF = model Feature

Figure S3: brain maps of maximum age correlation across all levels of the multi‐scale brain partition revealed by probabilistic tractography. Similar to Figure 3 for the linear case, but using probabilistic tractography.

Figure S4: Correlation with age in the circuit connectivity in comparison to the hippocampus circuit. The fronto‐striato‐thalamic and hippocampal features within the BCA model (with K = 38 features) with highest correlations with age are shown. Note the two are external SC features, specifically the number 1 in the Table S1 corresponding to the FST circuit and the number 7 for the hippocampus circuit. Values of Pearson's correlation c and p values are also given. Shaded region represents 95% confidence interval for the regression estimate.

Table S1: Module level in the brain hierarchical atlas and connectivity class (FC/SC or external/internal) for each of the K = 38 optimal features used for BCA.

Bonifazi P, Erramuzpe A, Diez I, et al. Structure–function multi‐scale connectomics reveals a major role of the fronto‐striato‐thalamic circuit in brain aging. Hum Brain Mapp. 2018;39:4663–4677. 10.1002/hbm.24312