Correspondence between evoked and intrinsic functional brain network configurations

Abstract

Much of the literature exploring differences between intrinsic and task‐evoked brain architectures has examined changes in functional connectivity patterns between specific brain regions. While informative, this approach overlooks important overall functional changes in hub organization and network topology that may provide insights about differences in integration between intrinsic and task‐evoked states. Examination of changes in overall network organization, such as a change in the concentration of hub nodes or a quantitative change in network organization, is important for understanding the underlying processes that differ between intrinsic and task‐evoked brain architectures. The present study used graph‐theoretical techniques applied to publicly available neuroimaging data collected from a large sample of individuals (N = 202), and a within‐subject design where resting‐state and several task scans were collected from each participant as part of the Human Connectome Project. We demonstrate that differences between intrinsic and task‐evoked brain networks are characterized by a task‐general shift in high‐connectivity hubs from primarily sensorimotor/auditory processing areas during the intrinsic state to executive control/salience network areas during task performance. In addition, we demonstrate that differences between intrinsic and task‐evoked architectures are associated with changes in overall network organization, such as increases in network clustering, global efficiency and integration between modules. These findings offer a new perspective on the principles guiding functional brain organization by identifying unique and divergent properties of overall network organization between the resting‐state and task performance. Hum Brain Mapp 38:1992–2007, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

A great deal of fMRI research has been devoted to the study of correlated spontaneous fluctuations in the blood oxygen level‐dependent (BOLD) signal between areas of the brain while participants are at rest (e.g., lying still with eyes closed or staring at a fixation cross) [Biswal et al., 1995; Buckner et al., 2009; Bullmore and Sporns, 2009; Calhoun et al., 2008; Fox and Raichle, 2007; Fox et al., 2005; Greicius et al., 2003]. This observed functional network organization is often considered “intrinsic,” meaning that such organization emerges in the absence of external stimulation. A question under active investigation is the nature of the modulation of this intrinsic organization by the administration of stimuli or task demands. Previous studies have emphasized the consistency of intrinsic functional connectivity from rest to various tasks [Buckner et al., 2009], while others have emphasized significant reorganization from rest to task [DeSalvo et al., 2014; Fransson, 2006; Hasson et al., 2009; Tomasi et al., 2014]. For example, Calhoun et al. [2008] and Fransson [2006] found that the same brain areas functionally connected at rest were connected during task performance (auditory oddball and 2‐back working memory tasks, respectively), but both found that the spatial extent of this connectivity was modulated during the task. More recently, Cole et al. [2014] demonstrated a high degree of correspondence between functional connectivity estimates at rest and during a variety of task scans across two large datasets. The spatial correlation estimate in functional connectivity values between the averaged multi‐task network and resting‐state network was surprisingly strong (i.e., r = 0.90 for both datasets). However, a small task‐dependent re‐organization of functional connectivity was observed as well that was consistent across all tasks, suggesting a task‐general change in functional connectivity from rest.

While the findings from these studies are informative, the focus on correspondence in functional connectivity estimates between brain areas across rest and task may overlook important task‐dependent changes in hub organization or overall network topology. Such important overall network changes (e.g., a shift in concentration of hub nodes or a quantitative change in network integration) can occur even though there may be strong correspondence overall in the pair‐wise functional connectivity estimates between brain areas across rest and task scans. Thus, a focus on functional network organization, as opposed to overall correspondence in pair‐wise functional connectivity estimates, may reveal new insights into similarities and differences between intrinsic and task‐evoked brain architectures.

A graph theoretical approach is well suited to characterize these changes in network organization. Graph theory allows the representation and quantification of the functional relationships among brain areas described as networks of nodes and edges. Various graph‐theoretical methods have been developed to describe the organization and properties of networks. These metrics have been applied to numerous network types, including networks of social interactions, power grids, the internet, disease transmission, and functional and structural brain imaging data [Achard et al., 2006; Bassett et al., 2011; Simpson et al., 2013; Sporns, 2014; Telesford et al., 2011].

Previous graph theoretical studies examining changes in brain network organization from rest to task have been somewhat inconsistent in their findings. One issue with these studies is the use of between‐subject designs to study changes in network organization between intrinsic and task‐evoked architectures [Buckner et al., 2009; Di et al., 2013]. For example, Buckner et al. [2009] did not find any significant changes between rest and task scans in hub structure using separate samples of participants. However, it's difficult to determine in these studies whether differences in intrinsic and task‐evoked architectures are due to differing sample characteristics. Other studies have observed a shift in network organization from rest to task in several whole‐brain metrics and hub structure [Moussa et al., 2012; Rzucidlo et al., 2013; Stanley et al., 2015]. However, these studies were limited in sample size and only compared resting‐state to one or two tasks. To address these concerns, we used graph‐theoretical techniques on a large sample of individuals (N = 202) provided by the Human Connectome Project [HCP; Barch et al., 2013] and a within‐subject design in which resting‐state and several task scans are collected from the same participant, accounting for between‐subject variability in network organization. We assessed hub organization for all datasets to enable comparison of the anatomical distribution of hub nodes for each task and resting‐state dataset. Additionally, three widely‐used graph‐metrics were computed to assess differences in overall network organization between rest and task scans: clustering coefficient, global efficiency, and the ratio of between‐ to within‐module connections. We hypothesized that despite largely similar overall functional connectivity patterns between task and resting conditions, as previously demonstrated, overall functional changes in hub organization and network topology would be observed.

MATERIALS AND METHODS

Participants

Neuroimaging data from 202 unrelated, healthy, right‐handed adults (Mean age = 28.61 years (SD: 3.85, range: 22–36); 103 female) made available through the Human Connectome Project (HCP) 2014 release were used for this study. Participants were recruited from the surrounding area of Washington University (St. Louis, MO). All participants gave informed consent before participating in the study, as described in Van Essen et al. [2013]. Further demographic information is provided in Table 1. For each subject, 28 min of resting‐state fMRI data and 7 task scans (16 subjects had at least one scan missing) were used for analysis, resulting in a total of 1,583 scans overall.

Table 1.

Participant demographics. Demographic information on the participants included in this study (n = 202)

Age in years
M(SD)	28.61 (3.85)
Gender
# male(%)	99 (0.49)
# female(%)	103 (0.51)
Handedness
M(SD)	77.98 (20.2)
Race
White	134
Black	52
Asian/Pacific Is.	3
More than one	6
Unknown	7
Ethnicity
Not Latino/Hispanic	160
Latino/Hispanic	41
Unknown	1

Data Acquisition and Preprocessing

Whole‐brain echo‐planar imaging acquisitions were collected using multiband (factor 8) pulse sequences for fast TR sampling [Uğurbil et al., 2013] on a 3T Siemens Skyra scanner with a 32‐channel head coil (TR = 720 ms, TE = 33.1 ms, flip angle = 52°, FOV = 208 mm × 180 mm, matrix size = 104 × 90, 72 slices, 2 mm isotropic voxels). To reduce the signal loss and distortions from the high‐resolution acquisition, all rest and task runs were acquired in two encoding directions (right–left and left–right, respectively). Data were collected over the course of two scanning sessions, spanning 2 days. Resting‐state scans were collected on each day, but only the resting‐state scan for the first day was used in the current analysis. The 7 task scans were collected over the course of the 2 days.

Minimally preprocessed data provided through the HCP were used for further analyses. The minimal preprocessing pipeline involved gradient distortion correction, motion correction, registration to the Montreal Neurological Institute (MNI) template, and intensity normalization. The details of the minimal preprocessing pipeline are described in Glasser et al. [2013]. Additional preprocessing steps included demeaning, variance normalization (normalizing the data to their standard deviations from the mean, z‐score) and concatenation of the time series from the right–left and left–right scans, respectively for the resting‐state data and each task using the Connectome Workbench [Marcus et al., 2011]. Time courses were despiked using AFNI's 3dDespike, an interpolative scrubbing procedure, and the functional data were spatially smoothed (4mm full width at half maximum) using the Connectome Workbench. In addition, the time courses were detrended (linear and higher order polynomials), nuisance covariate regression was performed (Friston's 24 motion parameters, namely each of the 6 motion parameters of the current and preceding volume, plus each of these values squared, ventricle and white matter signals) and the time courses were band‐pass filtered (0.01–0.1 Hz) to isolate the low‐frequency band at which the BOLD signal is most correlated among brain regions [Fransson, 2005] using the Data Processing and Analysis for Brain Imaging (DPABI) toolbox [Yan et al., 2016]. While some studies [Cole et al., 2014] have not band‐pass filtered task fMRI data to preserve possible high‐frequency task‐activation information, band‐pass filtering in the low‐frequency range (0.01–0.1 Hz) was conducted to ensure that differences in network properties were not the result of differences in high‐frequency noise. No participants included in the analysis displayed gross motion (relative Root‐Mean Squared‐Framewise Displacement [Jenkinson et al., 2002]; RMS‐FD < 0.55 mm; [Satterthwaite et al., 2013]).

Task and Resting‐State Datasets

For the resting‐state scans (two 14 min sessions; 1,200 volumes each) subjects were instructed to lie with eyes open and stare at a white fixation cross on a dark background [Smith et al., 2013]. Seven task runs were also collected for each subject. The seven tasks were collected in the following order: n‐back working memory task (∼10 min, data missing from 4 participants), card guessing game (∼6:30 min, data missing from 3 participants), motor task (∼7 min, data missing from 2 participants), story‐comprehension task (∼8 min, data missing from 6 participants), theory of mind task (∼7 min, data missing from 5 participants), shape matching (∼6 min, data missing from 6 participants), and emotional face matching (∼4:30 min, data missing from 5 participants) (see Table I in Supplementary Materials and Methods). Here we refer to the tasks as the working‐memory task, gambling task, motor task, language task, social task, relational task, and emotion task, respectively. The resting‐state, working‐memory task, gambling task, and motor task were collected on day 1. The language task, social task, relational task and emotion task were collected on day 2.

A brief description of each task is presented here. For more details see Barch et al. [2013]. The working‐memory task was an N‐back task with 0‐back and 2‐back blocks with faces, places, tools, and body parts presented as stimuli. The gambling task was a card guessing game which involved guessing the number on a mystery card to win or lose money in “mostly win” or “mostly lose” outcome blocks. In the motor task participants were directed to perform particular motor movements from the fingers, toes or tongue in response to visual cues. The language task was a story‐comprehension task with interleaved blocks of brief auditory stories and simple arithmetic problems (e.g., “fourteen plus twelve.”). The social task was a Theory of Mind task where participants are presented with short video clips of either interacting or randomly moving shapes. In the relational task, participants are presented with pairs of objects and were told to distinguish them on participant or experimenter‐specified dimensions. In the emotion task participants were told to match emotionally expressive faces (e.g., angry or fearful) or shapes presented at different locations on a screen.

Network Construction

Following the approach of previous comparisons of rest and task scans [Buckner et al., 2009; Cole et al., 2014; Najafi et al., 2016], region‐of‐interest (ROI) time courses were extracted using a 264 ROI (6mm spheres) data‐driven functional parcellation scheme [Power et al., 2011; see Figure 1 in Supplementary Materials and Methods] and correlated across all ROIs to generate a correlation matrix of functional connectivity (FC) values between each pair of ROIs. Networks were then binarized using a proportional thresholding method, such that FC values above some arbitrary percent threshold were included as connections, while the rest were set to zero. The proportional thresholding method that fixes the number of connections across networks is preferred to a fixed threshold method (e.g., significance threshold), a method which is known to confound further analyses [van Wijk et al., 2010]. To ensure that analyses were not contingent upon the choice of one proportional threshold, all analyses were conducted across a variety of thresholds (top 10%, 15%, 20%, 25%, 30%, 35%, 40%, 45%, and 50%). A network was created for each condition (rest, working‐memory, gambling, motor, language, social, relational, and emotion), resulting in approximately 8 networks for each participant and 1,583 networks overall. In addition, to ensure results were not contingent on binarized networks, we performed a robustness analysis with weighted networks created with a low (50%) and high (20%) threshold and surviving connections were weighted by the magnitude of the Pearson correlation coefficient between the two nodes (negative weights were set to zero).

Figure 1.

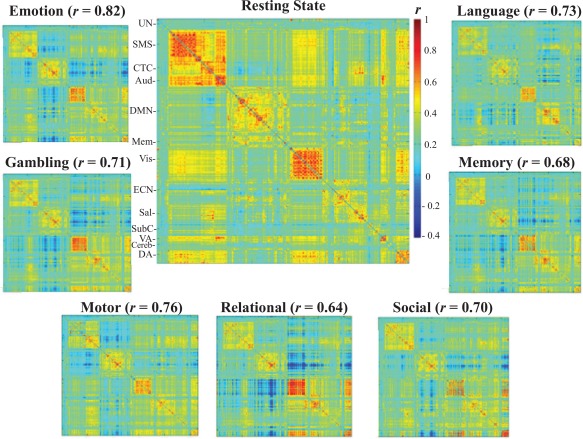
The spatial correlations between the average resting‐state FC matrix and the average task FC matrices. (Un—Uncertain, SMS—Sensorimotor, CTC—Cingulo‐Opercular task control, Aud—Auditory, DMN—Default Mode Network, Mem—Memory, Vis—Visual, ECN—Executive control (fronto‐parietal task control), Sal—Salience, SubC—subcortical, VA—Ventral Attention, Cereb—Cerebellum, DA—Dorsal Attention). The correlations range from 0.64 to 0.82 and demonstrate that the average FC matrices of rest and task scans are highly similar. [Color figure can be viewed at http://wileyonlinelibrary.com]

Hub Identification

To further explore differences in network organization between rest and task scans, differences in the spatial distribution of hub nodes between rest and task networks were examined. To examine hubs of resting and task scans we calculated node centrality using the GraphVar interface for Brain Connectivity Toolbox (BCT) functions [Kruschwitz et al., 2015; Rubinov and Sporns, 2010]. Because there are multiple measures of node centrality or “hubness” [Power et al., 2013; van den Heuvel and Sporns, 2013], the centrality of a node was calculated using four centrality metrics:

Degree Centrality (D): the number of connections of each node. Degree is the most commonly used metric for node centrality [Buckner et al., 2009; Tomasi and Volkow, 2011] and provides an estimate of how connected the node is to the rest of the network.

Closenness Centrality (C): the inverse of the mean distance (shortest path length) between the node and all other nodes in the graph [Freeman, 1978]. Nodes with high values of closeness centrality are “closer” in terms of geodesic distance, and exert greater influence in the network.

Eigenvector Centrality (E): the sum of the centralities of a node's directly connected neighbors [Lohmann et al., 2010]. Eigenvector centrality is derived from the eigenvector associated with the largest eigenvalue (λ₁, known as the first principal component) of the network matrix (i.e., matrix of 1's and 0's representing connections and non‐connections). A node with a large number of connections does not necessarily have a high eigenvector centrality, but is considered central if it connects to other important nodes.

Participation Coefficient (PC): the proportion of connections each node has outside of its own module (i.e., intermodular connections). Importantly, the calculation of participation coefficient (PC) requires an accurate parcellation of the network into modules, and here we adopted the standard a priori network partition of Power et al. [2011] for this purpose.

An overall centrality (D, C, E, and PC) for each node in every network was calculated by summing each node's centrality across threshold parameters from top 10% to top 50% thresholds in 1% increments [Power et al., 2013]. Those nodes in the top 10% of the distribution of centrality values for that network were considered hub nodes, consistent with thresholds used in previous studies [Bolt et al., 2016; Moussa et al., 2012; Rzucidlo et al., 2013]. The hub analysis was also conducted with a top 20% distribution threshold to ensure the results were not contingent upon the chosen top 10% threshold. Consistency of hub node classification (the number of times the node was classified as a hub) for that task scan was used as a measure of that node's importance for that task [Hayasaka and Laurienti, 2010; Moussa et al., 2012]. Nodes with high overlap of hub classification across networks were considered more central for that task. In addition to the binarized consistency approach for calculating hub centrality, we calculated weighted versions of the four centrality metrics (as described by Rubinov and Sporns [2010]) for weighted networks (top 50% and top 20% threshold) and averaged node centrality values across networks for each task. Nodes with higher average centrality values for that task were considered more central for that task.

To test for overall differences in the spatial distribution of hub nodes between rest and task scans, a recently developed permutation testing framework that takes into account the consistency of hub nodes within and between groups or conditions was implemented for each centrality metric [Simpson et al., 2013]. We briefly describe the approach here. The Jaccard index (JI), a similarity function used to quantify the union between two sets (e.g., networks), was used to quantify overlap in hub nodes between rest and task networks. If the two scans (e.g., Rest versus Emotion) are sufficiently different in the consistency in the spatial distribution of its hub nodes, it is expected that the calculated J will be, on average, smaller between scans, compared with the calculated J within the same scan. The ratio of the average within‐scan JI to average between‐scan JI, the Jaccard Ratio (R _JC), assessed differences in hub structure between resting and task scans. An R _JC > 1 indicates greater within‐scan similarity compared with between scan similarity, signifying the scans differ significantly in the spatial distribution of its hub nodes. An R_JC ≈ 1 indicates that there is no difference in the spatial distribution of hub nodes between the two scans. Because of the within‐subject design of the study, a paired two‐sample permutation test was used. Thus, to construct the null distribution of no differences between the two scans, the scan labels were permuted within each participant and the statistic was computed again for the permuted sample. This was repeated 100,000 times to construct a null distribution. The observed value was compared with the constructed null distribution to determine significance.

In addition to the test of overall differences in hub structure for each centrality metric, we examined the nodes with the top consistency values in both resting and task scans. Because the consistency values for all four centrality metrics were highly correlated in our data (see Fig. 2 in Supplementary Materials and Methods), we performed a principal components analysis (PCA) on the combined matrix of node × metric consistency values to form a single centrality or “hubness” metric, rather than examining each hub metric separately (D, E, C, and PC). This approach was conducted for both binary‐consistency and weighted approaches. The combined matrix was formed by first vertically concatenating the z‐scored matrix of node consistency values for each task, then horizontally concatenating the z‐scored consistency values for each metric into a 2,112 (node) × 4 (centrality metric) matrix. The first component was extracted and component scores were calculated for each node in each task on the first component. Of note, the loadings of each metric on the first component were approximately equal (D: 0.53, E: 0.5, C: 0.49, PC: 0.45 for the binary approach and D: 0.53, E: 0.54, C: 0.49, PC: 0.44 for the weighted approach). The score on this component represented a composite measure of the node's “hubness” (H) for that scan.

Whole‐Brain Network Metrics

Network metrics were calculated using BCT functions [Kruschwitz et al., 2015; Rubinov and Sporns, 2010]. The following metrics were calculated for each network:

Clustering Coefficient (CC): the fraction of a node's neighbors that are also neighbors of each other [Watts and Strogatz, 1998]. This was averaged across all nodes of the network to get an average CC for the network. Higher values represent the presence of more average clustered connectivity around individual nodes. As this value has been shown to be associated with average network density [van Wijk et al., 2010], values for each network were normalized to 20 corresponding random networks with preserved number of nodes, connections and degree distribution [Smit et al., 2008].

Global Efficiency (E _glob): is the inverse of characteristic path length, which is a measure of the average number of minimum connections that should be passed to join any two nodes in a network [Latora and Marchiori, 2001]. Global efficiency is a scaled measure that ranges from 0 to 1, with a value of 1 signifying maximum distributed processing. As this value has been shown to be associated with average network density [van Wijk et al., 2010], values for each network were normalized to 20 corresponding random networks with preserved number of nodes, connections and degree distribution.

Ratio of Between‐ to Within‐Module Connections: the average number of connections between nodes within a module divided by the average number of connections between nodes from different modules. The a priori parcellation of Power et al. [2012] was used as a high‐resolution modular partition to calculate within‐ and between‐module connections.

To ensure the results were robust to the thresholding method employed, weighted versions of these metrics were computed on weighted networks thresholded at a low (top 50%) and high (top 20%) threshold. The values for each network were normalized to 20 corresponding weighted random networks with preserved number of nodes, connections, and weight distribution.

Statistical Analysis of Whole‐Brain Network Metrics

To quantify differences in graph metrics across resting‐state and task scans, a linear mixed‐model with scan (e.g., rest and working‐memory) as a categorical factor and subject modeled as a random effect was performed for each metric. This statistical approach was chosen over the more common repeated‐measures ANOVA, which assumes a compound symmetry form of the within‐subject variance‐covariance matrix. However, this assumption is likely to be violated given the unequal intervals of collection, with some tasks collected on the same day, and others separated by a day. To correct for possible covariance differences among tasks that were/were not separated by scanning session, an unstructured covariance matrix was used in which all elements of the variance‐covariance matrix are estimated, rather than assuming a homogenous variance‐covariance matrix that may bias results. In addition, a summary motion statistic, average relative RMS‐FD and average respiration volume (RVT) that was derived from measurements from the Siemen's respiratory belt placed on the participant's abdomen during each scan (average RVT was calculated by simply averaging across the RVT time course from each scan) were included as covariates in the model, as motion and respiration are known to affect FC estimates [Birn, 2012; Power et al., 2012]. In addition, the same linear mixed‐modeling approach was used to estimate possible task‐general differences in average motion or respiration to ensure results were not driven by these effects. Parameters were estimated using the restricted Maximum Likelihood (ReML) method. All statistical analyses were carried out in the Statistical Package for the Social Sciences (IBM SPSS Statistics for MAC, Version 22.0).

Analyses Controlling for Task‐Activation Effects

To ensure that differences between rest and task network configurations were not driven by task‐related activations influencing task‐related functional connectivity, we conducted the above analyses with the blocked events from each task regressed out of each region's time series. This involved convolving regressors of each block from each of the seven tasks with a double‐gamma Hemodynamic Response Function (HRF), and fitting the task‐specific convolved block regressors to each region's time series from each subject using the General Linear Model (GLM). The residuals from this linear model were then used to calculate FC matrices. The graph‐theoretical results from this analysis were then compared with the original graph‐theoretical analyses.

RESULTS

Overall Task Versus Rest Correlations

To compare FC values between the resting‐state and the seven task scans, individual FC matrices for each scan were Fisher‐z transformed and then averaged across participants to form an average FC matrix for each scan (Fig. 1; average FC matrices were converted back to r values for presentation). Correlations between the resting‐state and task FC matrices reveal a moderate to strong degree of similarity between the rest and task scans in average FC values, ranging from r = 0.64 to r = 0.81 (emotion: r = 0.82, gambling: r = 0.71, language: r = 0.73, motor: r = 0.76, relational: r = 0.64, social: r = 0.70, working‐memory: r = 0.68).

Hub Nodes in Resting‐State and Task Scans

Networks were created at the individual level by binarizing each individual's FC matrix through proportional thresholding (see Network Construction). To explore differences in network organization between rest and task scans, node centrality metrics were computed for all individual networks. Hub nodes for each network were defined as those nodes in the top 10% of the summed‐over‐thresholds centrality distribution for that network. Permutation tests for each centrality metric were used to determine if there were any significant differences in the spatial distribution of hubs between rest and each task. The results reveal significant overall differences in the distribution of hub nodes between the resting‐state and each task scan for all centrality metrics (all p < 0.05; corrected for multiple comparisons; see Table II in Supplementary Materials and Methods). Overall, the emotion task was most similar to the resting‐state (M _JC = 1.23), while the social task was most dissimilar to the resting‐state (M _JC = 1.44).

A PCA was used to derive a single composite “hubness” metric (H; see Hubness Identification in Materials and Methods) from the four centrality metrics examined. Component scores for each node on the first component (which explained 86.59% of the variance in the 4 centrality metrics) represented its hubness score. Correlations between resting‐state and task hubness values reveal a moderate to strong correspondence in hub nodes between the resting‐state and task‐scans, ranging from r = 0.59 to r = 0.75 (emotion: r = 0.75, gambling: r = 0.68, language: r = 0.61, motor: r = 0.7, relational: r = 0.62, social: r = 0.59, working‐memory: r = 0.61; Fig. 2). The hubness analysis at a top 20% distribution threshold produced similar results; the correlation of hubness scores between both thresholds was r = 0.983.

Figure 2.

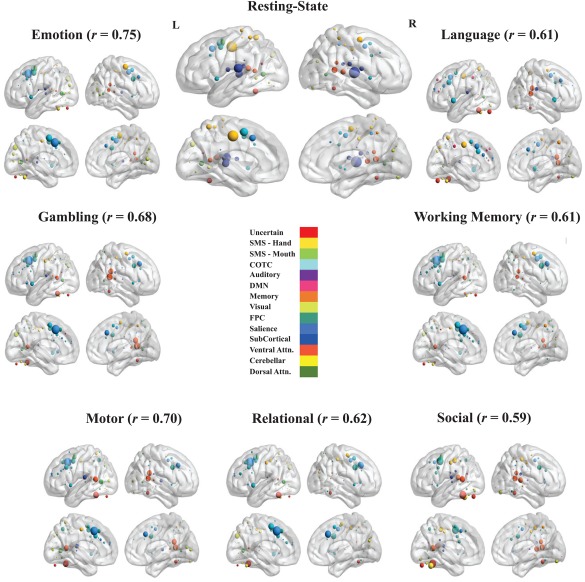
Hub node visualization for rest and task scans (SMS—Sensorimotor, CTC—Cingulo‐Opercular Task Control, DMN—Default Mode Network, Memory—Memory Retrieval, FPC—Fronto‐Parietal Task Control, Ventral Attn.—Ventral Attention, Dorsal Attn.—Dorsal Attention). ROIs were placed on a smoothed brain surface using BrainNet Viewer [Xia et al., 2013]. Nodes from different modules were differentiated by color (the Power et al. [2011] network parcellation consists of 14 modules). Node size was scaled by the “hubness” of that node for that scan, as defined above; i.e. the component score of that node on the first principal component derived from the four centrality metrics. Brain images were thresholded at z > 0. Above each brain figure is the correlation between the hubness values of each node between the resting‐state and that task scan. [Color figure can be viewed at http://wileyonlinelibrary.com]

To examine whether the differences in hub organization from the resting‐state were task‐general, rather than unique to each task, we also examined whether hub organization was more similar between tasks than between each task and the resting‐state. For each task, a modified z‐test for assessing the significance of the difference between two dependent correlation coefficients [Steiger, 1980] was used to test whether the average correlation in hubness values between that task and all other tasks was stronger than the correlation between that task and the resting‐state (the correlation coefficients are dependent, as they share a common variable in both correlations—the task scan). The results reveal that for each task, the average task correlation is significantly greater than the correlation between that task and the resting‐state ( $\overline{r}$ _emotion = 0.82, p = 0.022; $\overline{r}$ _gambling = 0.87, p _gambling < 0.0001; $\overline{r}$ _language = 0.75, p _language < 0.0001; $\overline{r}$ _motor = 0.83, p _motor < 0.0001; $\overline{r}$ _relational = 0.83, p _relational < 0.0001; $\overline{r}$ _social = 0.71, p _social = 0.0017; and $\overline{r}$ _{working‐memory} = 0.84, p _{working‐memory} < 0.0001; uncorrected for multiple comparisons as the analyses were not statistically independent).

Networks were visualized for the resting‐state and each task scan, and node size was made proportional to the number of times that node is classified as a hub across all subjects for that scan (Fig. 2; the top 10 nodes for each scan are displayed in Table III in Supplementary Materials and Methods). Despite a moderate to strong overall correspondence in hub organization, examination of hub nodes between rest and task scans reveals a shift in the concentration of hub nodes from primary sensory and motor areas (somatosensory and auditory) for resting‐state to nodes in the executive control, salience, and ventral and dorsal attention modules for task scans. The most consistently identified hub nodes across subjects in the resting‐state were in the auditory and somatosensory modules (as classified by Power et al. [2012]). The most consistently identified hub node was located in the left superior temporal gyrus and a part of the auditory module (H = 8.32). Other prominent hub nodes in the resting‐state included a somatosensory node located in the middle cingulate cortex (H = 8.28), two auditory nodes in the right superior temporal gyrus (H = 6.98), and a cingulo‐opercular task control node in the middle cingulate/dorsal anterior cingulate cortex (H = 6.26).

In contrast, the most consistently identified hub nodes for each task scan were found in the fronto‐parietal task control, cingulo‐opercular task control, salience, and ventral attention modules. For the majority of task scans (emotion, gambling, motor, relational and working‐memory), a salience module node in the dorsal anterior cingulate cortex (dACC) was the most consistently identified hub node (H's > 8). In the resting‐state, this salience module node is less prominent (H = 4.99) compared with the auditory and somatosensory nodes described above. In addition to the salience module node, there was a strong concentration of hub nodes in and around the anterior mid‐cingulate/dorsal anterior cingulate cortex (aMCC/dACC) for each task scan, areas associated with salience and cingulo‐opercular modules. Other prominent task scan nodes include two ventral attention module nodes in the right supramarginal gyrus (in the motor, language, gambling and social tasks; $\overline{H}=5.8$) and a fronto‐parietal module node (in the emotion, social and working‐memory tasks $\overline{H}=6.7$) in the left dorsolateral prefrontal cortex. In addition, a node in the left fusiform gyrus was found to be a prominent hub in the social, gambling, language, motor and relational task scans ( $\overline{H}=6.44)$, and a visual module node in the left occipital cortex was found to be a prominent hub node in the emotion, relational and gambling task scans $(\overline{H}=5.22)$.

The dACC did not emerge as the most consistently classified hub node in the social and language task; it was the 5th most consistent node in the language task. The most consistent node in the language task was a sensorimotor module node located in the mid‐cingulate cortex; this was also a prominent hub node in the resting‐state. The social task had the most unique hub organization of the task scans ( $\overline{r}$ _social = 0.71), and was the most dissimilar to the resting‐state compared with other task states (M _JC = 1.23) in the binary consistency approach. The most consistent node in the social task was in the left fusiform gyrus (H = 7.99) that was not classified into a known module in the original Power et al. [2011] parcellation. In addition, the only prominent non‐cortical hub was a node in the left cerebellum associated with the social task (H = 6.12).

To ensure the results were not limited to the binary‐consistency approach used here, a PCA was applied to the same four centrality metrics calculated on weighted networks thresholded at top 50% and 20% proportional thresholds. Instead of examining consistency of the top 10% hub nodes across subjects, node values were averaged across subjects for that task. The weighted network and binary‐consistency approaches produced similar results: node component scores from both approaches are strongly correlated at both the top 50% (r = 0.78) and top 20% (r = 0.75) thresholds, with the same top nodes for each scan being implicated in both methods (see Figs. 3 and 4, and Tables IV and V in Supplementary Materials and Methods). However, in the weighted network approach, the shift in hub organization from primary sensorimotor nodes to fronto‐parietal, cingulo‐opercular task‐control and salience nodes between rest and task states was more prominent, with increased hubness values in auditory and sensorimotor module nodes in the resting‐state and increased hubness values in salience, fronto‐parietal and cingulo‐opercular task‐control nodes in task scans. For example, for both weighted approaches, only one node outside of the primary sensory/motor or subcortical areas in the resting‐state was observed in the top ten strongest hub nodes, the previously mentioned cingulo‐opercular task control node in the middle cingulate/dorsal anterior cingulate cortex (Tables IV and V in Supplementary Materials and Methods). In addition, the overall correspondence of hubness values across ROIs between the resting‐state and task scans was smaller in the weighted network approach for both top 50% and top 20% thresholds (Figs. 3 and 4 in Supplementary Materials and Methods).

Whole‐Brain Network Metrics

The following results are reported using a top 20% threshold, but analyses were run across a range of thresholds to determine the influence of threshold choice on the results (Fig. 3). A linear‐mixed model with average motion (relative root mean square displacement) and average respiration (average respiration volume per unit time) as covariates and resting‐state and task scans (e.g., rest, working memory) as a categorical factor was used to determine if there were any differences in network organization between resting‐state and task scans.

Figure 3.

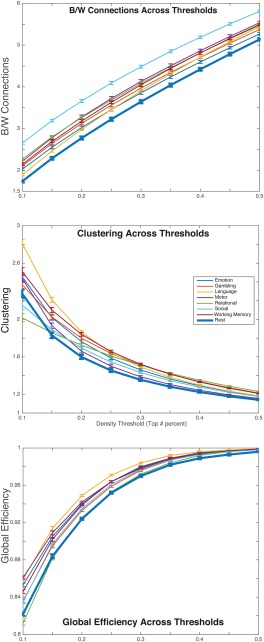
All three of the metrics for rest and each task scan plotted (with standard error bars) across 9 density (proportional) thresholds (0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5). For each graph, metric values are plotted along the vertical axis and thresholds are plotted along the horizontal axis. The rest and task scans are represented by different colored lines (resting‐state values are represented by the thick dark blue line). The results reveal a task‐general change from rest to task (excluding the relational task for clustering and global efficiency) in clustering, global efficiency and between‐ versus within‐module connections. [Color figure can be viewed at http://wileyonlinelibrary.com]

A linear mixed model revealed that there were significant differences among the scans in local clustering (i.e., clustering coefficient), F(7,265.34) = 30.844, p < 0.001. To determine whether there were any significant differences in clustering coefficient between rest and task architectures, individual post‐hoc t‐tests (Bonferroni corrected for multiple comparisons) were performed between the estimated marginal means (i.e., mean of each task scan adjusted for covariates) of the resting‐state and each task scan. The results revealed greater (p < 0.05) local clustering for each task scan, excluding the motor task, compared with the resting‐state (Fig. 3). These results were independent of threshold effects at most thresholds (0.2–0.5), but at the most stringent thresholds (top 10% and 15% connections) the differences between rest and some task scans were no longer significant (15%: social p = 1; 10%: social: p = 0.335, gambling: p = 1). However, at the high degree of sparsity enforced by these stringent thresholds (top 10% and 15%) some networks can become fragmented. For example, at the top 10% threshold close to half of the networks, N = 657, have more than ten nodes removed from the main component of the network. Thus, differences between resting‐state and task scans are expected to be smaller at the most stringent thresholds.

A linear mixed model revealed that there were significant differences among the scans in global efficiency, F(7,207.877) = 63.094, p < 0.001, and average respiration (RVT) was found to be a significant predictor of global efficiency, F(1,832.589) = 5.705, p = 0.017. Post‐hoc t‐tests between rest and task scans revealed greater distributed, global organization in task scans (excluding the relational task) compared with rest (Fig. 3). These results were independent of threshold effects, as they were observed at all thresholds including the most stringent threshold of 10%.

A linear mixed model revealed that there were significant differences among the scans in the ratio of between‐to‐within module connections F(7,269.47) = 36.07, p < 0.001, and average motion was found to be a significant predictor of the ratio of between‐to‐within module connections F(1,468.583) = 5.273, p = 0.022. Post‐hoc t‐tests between rest and task scans revealed a greater number of between‐module connections compared with within‐module connections in task scans compared with rest (Fig. 3). These results were observed at all thresholds.

To ensure these results were not contingent upon a binarized approach, we applied the same analyses to weighted metrics computed on weighted networks thresholded at a low (top 50%) and high (top 20%) proportional threshold (see Fig. 5 in Supplementary Materials and Methods). Consistent with the binarized results, weighted clustering and the ratio of between‐ to within‐module connections was significantly greater in task scans compared with rest at both thresholds. Inconsistent with the binarized results, only one task scan (motor task) was significantly greater in global efficiency than rest at the 20% threshold, and resting‐state was greater in global efficiency than all tasks, excluding the motor task at the 50% threshold. One potential reason for the reversal of the pattern of binary global efficiency is that the weighted global efficiency metric is computed using the sum of the weights of traversed connections, and the resting‐state has higher average weight compared with task scans at the top 50% threshold (M _Rest = 0.4601; M _Task = 0.4305). In fact, at the top 50% threshold, average weight is strongly positively correlated with global efficiency (r = 0.76).

Confound and Reliability Analyses

Several motion‐correction preprocessing steps were applied to the data, and no participants included in the analysis displayed gross motion (relative RMS‐FD < 0.55 mm; [Satterthwaite et al., 2013]). Additionally, subject‐level differences in motion and respiration were covaried out of the group‐level analysis. But to further ensure that the observed task‐general changes in network metrics were not due to subject‐level motion and/or respiration differences, a linear‐mixed model was used to estimate any differences among rest and task scans in average motion (relative RMS‐FD) and average respiration (RVT). The tests of the overall model fits were significant (relative RMS‐FD: F(7,194.55) = 4.395, p < 0.001; RVT: F(7,165.95) = 17.95, p < 0.001), indicating significant differences in average motion and average respiration between at least two pairs of conditions. However, pairwise t‐tests between rest and task scans for both models indicate that for motion, there were no significant differences between rest and task scans (p > 0.05, uncorrected for multiple comparisons), and for respiration, there were no systematic differences in average RVT between rest and task scans: working‐memory (p = 0.017), gambling (p = 0.013), language (p = 0.013), and relational (p < 0.001) had significantly greater average RVT compared with rest, and emotion (p < 0.001) had significantly less average RVT (p < 0.001; there were no significant differences for motor or social). In addition, the significance of these differences did not survive multiple comparison correction (Bonferroni). Thus, task‐general differences in motion and respiration could not explain the observed task‐general changes in network organization.

Differences in duration between the task and rest scans present another potential confound. The resting‐state scan was collected for 30 min, while all task scans run times were collected in under 10 min. Thus, resting‐state functional connectivity matrices may differ from task scan functional connectivity matrices because of more accurate functional connectivity estimates in the resting‐state scan. To explore this possibility, we calculated functional connectivity matrices for each participant from randomly‐chosen 7 min of continuous resting‐state data (the mean amount of time for the task scans). We find that the average resting‐state matrix calculated from the 7 min of data was nearly identical to the average resting‐state matrix calculated from the original 30 min of resting‐state: r = 0.997. Thus, 7 min of the resting‐state fMRI data produced reliable FC estimates that were almost indistinguishable from 30 min of resting‐state fMRI data. This is consistent with earlier observations that pair‐wise functional connectivity estimates stabilize around 4‐5 min of acquisition time [Van Dijk et al., 2010]. In addition, as shown above (Fig. 1), the average emotion task functional connectivity was most similar (r = 0.82) to the average resting‐state functional connectivity matrix, despite the fact that emotion task scans was derived from the shortest amount of scan time (∼4:30 min).

A split‐half reliability analysis was conducted at the 20% proportional threshold in which the sample was randomly split into two equal halves (n = 101), and the same linear‐mixed model performed on both (Fig. 4). Correlations among the estimated marginal means for each network metric revealed strong reliability across halves (Between/Within Connections: r = 0.93, Global Efficiency: r = 0.91, Clustering: r = 0.75).

Figure 4.

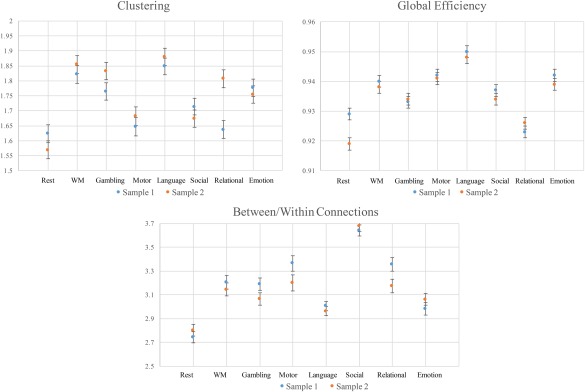
The estimated marginal means (with error bars) for each whole‐brain network metric across the two split‐half samples. Metric values are plotted along the horizontal axis and task labels are plotted along the horizontal axis. Means for sample 1 are plotted in blue and means for sample 2 are plotted in orange. The results reveal that clustering, global efficiency and ratio of between‐ to within‐module connections were sufficiently reliable across split‐half samples. [Color figure can be viewed at http://wileyonlinelibrary.com]

Comparison of Original and Regressed Task Networks

One possible objection to the network estimation approach used in the current study and others [Buckner et al., 2009; Finn et al., 2015; Najafi et al., 2016; Rzucidlo et al., 2013; Shirer et al., 2015] is that task‐activation confounds potential network connection estimates, such that areas that are highly activated during a task are artificially estimated to have higher centrality estimates (or “hubness” estimates in our approach), or that activations throughout the cortex confound whole‐brain network estimates. Thus, we sought to demonstrate that the above results were not driven by task‐related activations by regressing out task‐related events from each task and recalculating the graph‐theoretical metrics.

The results reveal that the regression of task events had minimal effects on the results (Fig. 5). The average similarity between the task FC matrices before and after the regression step was r = 0.96 (0.92 < r < 0.99). The average similarity between the task hubs before and after the regression step was r = 0.95 (0.84 < r < 0.99). The only task with noticeable change of hub organization was the social task (r = 0.84). In particular, the regression of task events increased the average similarity between the social task and other task scans ( $\overline{r}$ _social = 0.79) and shifted the salience module node in the dACC to the most prominent hub node in the social task, consistent with the other task scans. As previously demonstrated by Cole et al. [2014], the regression of task events had the effect of increasing the average similarity between the resting‐state and the task scans in both FC matrices ( $\overline{r}$ _change = 0.09) and hub organization ( $\overline{r}$ _change = 0.07). As with the hub estimates, the regression of task events had only minimal effects on whole‐brain network connection estimates. In particular, at the top 20% proportional threshold the regression of task events had the effect of slightly increasing global efficiency estimates (average increase in 0.011) and slightly decreasing clustering and between‐versus‐within module connection estimates (average decrease in 0.05 and 0.06, respectively). In addition, the task‐general increase in all three whole‐brain metrics is present in the regressed data as well as the original (see Table VI in Supplementary Materials and Methods).

Figure 5.

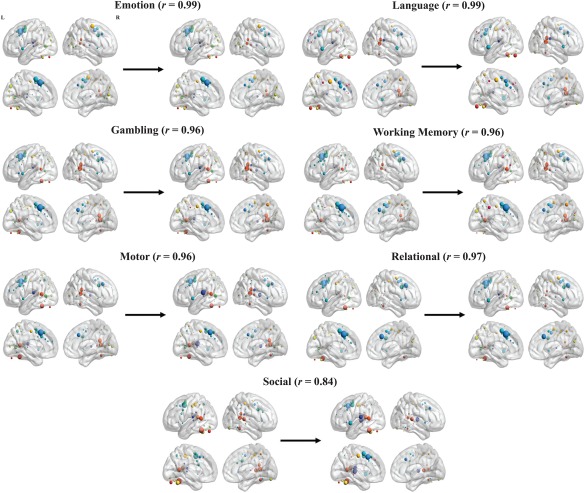
Comparison of node hubness values, with associated correlation values, before and after the regression of the convolved task block regressors. Node hubness was visualized in the same manner as Figure 2. Arrows and the values above them represent the correlation in hubness values across ROIs between the original (left) and regressed (right). The results demonstrate that the regression of task events had minimal effects on the hubness estimates. [Color figure can be viewed at http://wileyonlinelibrary.com]

DISCUSSION

The relationship between intrinsic and task‐evoked activity in the human brain is complex and incompletely characterized. Recently, there has been a renewed interest in the application of data‐driven approaches to understanding the relationship between resting‐state and task activity in the brain [Cole et al., 2014; DeSalvo et al., 2014; Di et al., 2013; Najafi et al., 2016; Telesford et al., 2016]. Here, we take an exploratory approach, using graph‐theoretical techniques to quantify various properties of network organization across a large sample of individuals performing a wide variety of cognitive tasks. The results reveal that despite moderate to strong overall correspondence in network organization, significant task‐general differences between resting‐state and task architectures in both hub structure and overall network organization were observed. These results suggest that considering rest‐to‐task FC changes from a graph‐theoretical perspective may yield additional insights into network organizational differences between wakeful rest and task performance beyond simply comparing the spatial correlation in FC values between these conditions. Thus, while comparing the strength of similarity between pair‐wise functional connectivity estimates between rest and task scans is informative, the graph‐theoretical analysis used here provides further insight into differences into brain network topology across varying conditions.

Hub Analysis

The results of the hub analysis revealed a task‐general change in the concentration of hub nodes between resting and task scans, as measured by a linear combination of four centrality metrics. Such findings are in agreement with findings that the hub architecture of the brain is not stable from rest to task scans [Di et al., 2013; Moussa et al., 2011]. In particular, there was a shift in the concentration of hub nodes in the primary sensory and motor modules at rest to a shift in the concentration of hub nodes in the salience, fronto‐parietal, ventral attention, and cingulo‐opercular task control modules [Seeley et al., 2007; Uddin, 2015] for both binary and weighted hub approaches. The most prominent node in the resting‐state was an auditory module node located in the left superior temporal gyrus, which was identified as a possible hub region in van den Heuvel and colleagues' [2008] study of resting‐state functional connectivity. Other graph‐theoretical studies of resting‐state functional connectivity, primarily using degree centrality as a measure of hubness, have identified default mode network regions, along with some evidence for sensorimotor and fronto‐parietal regions, as resting‐state hubs [Buckner et al., 2009; Tomasi and Volkow, 2011; van den Heuvel and Sporns, 2013]. However, the sole use of degree centrality [Power et al., 2013], or any single a measure of hubness [Zuo et al., 2012] may bias the detection of hub regions. Thus, the discrepancy in findings between the current results and previous studies may be the use of a single measure of hubness in previous studies that does not incorporate other centrality information. Here we included a weighted combination of several commonly used centrality measures to create a composite score to allow us to quantify functional connectivity hubs.

A node in the dACC of the salience module emerged as the most consistently identified hub node across subjects for five task scans. Other nodes in the mid‐cingulate/dorsal anterior cingulate, comprising cingulo‐opercular and salience nodes, were also found to be highly consistent hub nodes across subjects for each task scan. This finding suggests a particularly important role for the aMCC/dACC in the maintenance of the sustained cognitive processes associated with task performance. Previous research has established the dACC as a particularly important network hub in the human brain during cognitive control tasks [Cole et al., 2010; Cole and Schneider, 2007; Duncan and Owen, 2000; van den Heuvel and Sporns, 2013]. Duncan and Owen [2000] found that this area was activated across a range of tasks requiring different cognitive demands. In addition, it has been found to be one of the most globally connected areas of the cortex [Cole et al., 2010]. It is thought that this area has an important role in coordinating information across many areas of the brain [Cole and Schneider, 2007; Margulies et al., 2007]. Within the context of the salience network, the dACC is thought to facilitate response selection and motor response [Menon and Uddin, 2010]. It should be noted that activations in the dACC are among the most widely reported in the cognitive neuroscience literature [Behrens et al., 2013], and have been linked to processes ranging from pain perception [Wager et al., 2013] to empathy and social cognition [Singer and Klimecki, 2014].

As demonstrated in the analysis conducted on data with task‐activations regressed out using the GLM, the hub findings were not dependent on spurious connectivity between regions as the result of common activation to trial onsets and offsets. Overall, the regression of task‐activation had the effect of increasing the average hub similarity between resting‐state and task scans. Interestingly, the regression of task‐activation had a larger effect on the social task (r = 0.84 of hub organization before and after the regression step), which had the effect of significantly increasing its similarity in hub organization with the other tasks. This may be because of differential fit of the task reference function for the social task, compared with the other tasks.

Of note is that the strength of similarity in hubness values between resting‐state and task scans was not entirely consistent between the binary‐consistency and weighted average approaches. In particular, the overall correlation in hubness values between resting‐state and task scans was smaller in the weighted‐average approach compared with the binary‐consistency approach, and the ordering between tasks in terms of similarity to the resting‐state was different between the two approaches. The primary difference between the binary and weighted approach is explained by the importance given to the consistency of hub classification and the average magnitude of hubness across participants, respectively. Thus, while both approaches give similar estimates of hubness overall for each scan, differences may still be present given the importance assigned to each criteria in the two approaches.

Whole‐Brain Network Organization

The results from our analysis of overall network topology are in agreement with previous findings demonstrating the modulation of overall functional network topology in response to task demands [Bassett et al., 2011; Di et al., 2013; Heitger et al., 2012; Rzucidlo et al., 2013; Stanley et al., 2014, 2015]. In particular, there was greater clustering, global efficiency and between‐versus‐within module connections during task performance compared with during the resting‐state. This is consistent with the idea that the increased cognitive demands associated with task performance requires increased integration or communication between nodes and modules of the network [Bassett et al., 2011; Cole et al., 2013; Kitzbichler et al., 2011]. Given the increased requirement for coordinating processes across various modalities during task performance, a shift from a more modular, clustered organization to a more integrated organization would be expected. Of note is the fact that the global efficiency results did not replicate for weighted networks. It is probable that this discrepancy is explained by significantly greater average connection weights in the resting‐state compared with task scans, as the weighted global efficiency metric has been previously shown to be strongly dependent on and even equivalent to average edge weight under certain mild conditions, specifically when minimum edge weight is greater or equal to half the maximum edge weight of the network [Ginestet et al., 2014]. However, if one controls for this initial difference in weights by using a binary threshold, global efficiency is greater in task scans compared with the resting‐state.

We hypothesize that the domain‐general cognitive processes associated with the shift from wakeful rest to task performance may be a shift from mind‐wandering and internally‐directed attention [Gusnard et al., 2001] in the resting‐state, to externally‐directed attention and cognition in response to task‐associated stimuli. Thus, it may be that the increased attentional demands associated with task performance may require a shift to more locally specialized information processing and more distributed, parallel information processing compared with the resting‐state. The task‐general increase in hubness values from rest to task scans in executive control, cingulo‐opercular and salience module areas indicates that these domain‐general processes involve task‐general executive control and attentive processes. Because these changes are observed across a variety of task states, these results point to a “task‐general” network and associated hub organization that facilitates the information‐processing demands of these cognitive processes, not observed in resting wakefulness. In particular, the perception and subsequent processing of stimuli seems to require increased network integration between nodes and modules of the network. Nodes in the salience, executive control and cingulo‐opercular modules are central hubs in this more integrated network. Future studies are needed to explore the potential role of this task‐general network change for domain‐general cognitive processing.

Limitations

It is important to note that while overall global network measures, as opposed to individual node centrality estimates, may have a consistent interpretation in social networks and some communication networks, their interpretation is less clear in a brain network, particularly in the case of functional connectivity networks. In functional connectivity approaches, the nature of edges of the network (statistical dependence between nodes) may not lend itself to a straightforward information‐processing interpretation. Despite this difficulty, given the task‐general change in network organization, it is likely that these changes from rest to task scans are associated with domain‐general cognitive processes related to these tasks, and these changes are likely to have an effect on the information‐processing capacities of the brain during that task. This is consistent with observed associations between functional connectivity derived whole‐brain network organization and task performance [Moussa et al., 2014; Stanley et al., 2014; Stevens et al., 2012]. Another limitation of the current study is the lack of counterbalancing in the task fMRI collection of the HCP. Because of this, it is impossible to separately estimate or remove possible order effects in the data. This is an important design procedure [Buračas and Boynton, 2002; Wager and Nichols, 2003] and is often not considered in many repeated‐measures task‐fMRI paradigms.

CONCLUSIONS

Understanding the complex relationship between intrinsic and evoked activity in the human brain requires data‐driven, whole‐brain approaches to characterizing network topology. Using a large sample of individuals and a within‐subject design, we examined differences in functional network organization between intrinsic and a variety of task‐evoked architectures. While we observed relatively high correlations in average FC values between intrinsic and task‐evoked architectures, our results reveal a task‐general shift in network organization, as revealed by changes in hub structure and whole‐brain network metrics. Importantly, we observed a significant shift in the anatomical distribution of hub nodes from rest, where hubs were primarily concentrated in sensorimotor and auditory modules, to task, where hubs were primarily concentrated in the salience and control modules. In particular, a node located in the mid‐cingulate/dorsal anterior cingulate cortex was found to be the most central hub region across most task scans. These results add to a growing body of literature suggesting that specific hubs in the brain play a more central role in the coordination of neural resources in the service of goal‐directed behaviors [Dosenbach et al., 2008; Uddin, 2015].

Supporting information

Figure S1. Power 264 Functional Parcellation. The 264 nodes of the Power et al. [2011] parcellation placed in their respective MNI coordinates. Nodes are colored by their module assignment.

Figure S2. Correlations between centrality metrics. (D = Degree Centrality, C = Closenness Centrality, and E = Eigenvector Centrality, PC = Participation Coefficient,). This figure displays the correlations (with corresponding p‐values and number of observations) between hub node consistency (z‐scored) defined for all four centrality metrics. The results show that the centrality metrics are strongly correlated.

Figure S3. Hub node visualization for weighted‐average approach at Top 50% Density. (SMS—Sensorimotor, CTC—Cingulo‐Opercular Task Control, DMN—Default Mode Network, Memory—Memory Retrieval, FPC—Fronto‐Parietal Task Control, Ventral Attn. —Ventral Attention, Dorsal Attn. —Dorsal Attention). ROIs were placed on a smoothed brain surface using BrainNet Viewer [Xia et al., 2013]. Nodes from different modules were differentiated by color (the Power et al. [2011] network parcellation consists of 14 networks). Node size was scaled by the “hubness” of that node for that state, as defined above; i.e. the component score of that node on the first principal component derived from the four centrality metrics. Brain images were thresholded at the value corresponding to the 10th percentile of the distribution of hubness values (i.e., only nodes in the top 10% of hubness values were displayed). Above each brain figure is the correlation between the hubness values of each node between the resting‐state and that task scan. Results reveal that the weighted‐average approach is consistent with the binary‐consistency approach.

Figure S4. Hub node visualization for weighted‐average approach at Top 20% Density. The same procedure used to calculate and visualize node hubness for the top 50% density threshold was used for the top 50% threshold. The hubness values across thresholds (top 20% and top 50%) are strongly correlated (r = 0.94).

Figure S5. Weighted graph metrics between rest and task states across a low and high proportional threshold. All three of the metrics for rest and each task state displayed in a bar graph (with standard error bars) across 2 density (proportional) thresholds: top 20% and top 50% threshold. For each graph, metric values are plotted along the vertical axis and the two thresholds are plotted along the horizontal axis. The rest and task states are represented by different colored bar (resting‐state values are represented by the yellow bar). The results are consistent with the binarized results for clustering and between‐ versus within‐module connections. Inconsistent with the binary results, there is no task‐general change in global efficiency at the top 20% threshold (only the motor task is significantly greater in global efficiency) and the task‐general change is reversed in the global efficiency, such that there is significantly greater global efficiency in the resting‐state compared to task states.

Table SI. Task Descriptions and Durations. Brief descriptions of each task scan included in the analysis, along with the durations and the number of participants that completed each scan. Note, that the task scans were completed in two sessions separated by a day

Table SII. Jaccard Ratio between Rest and Task Scans. The Jaccard Ratio (R_JC), or the ratio of within‐condition similarity to between‐condition (between rest and task condition) similarity across all participants for each centrality metric, and associated significance values (adjusted for multiple comparisons using the Bonferroni‐Holm procedure [Holm, 1979]) from the permutation test testing the difference in similarity in hub nodes between rest and task conditions

Table SIII. Coordinates and descriptions of top 10 hub nodes for binarized‐consistency approach. A companion figure to figure 2. This table displays the anatomical location of the top 10 consistently identified hubs according to the Montreal Neurological Institute (MNI) coordinates of that node, along with the network to which each node belongs, as found in Power et al. [2011]. In addition, the hubness score (component score on the first principal component derived from the four centrality metrics) is displayed for each node

Table SIV. Coordinates and descriptions of top 10 hub nodes for weighted‐average approach at top 50% density. A companion figure to figure D. This table displays the anatomical location of the top 10 consistently identified hubs according to the Montreal Neurological Institute (MNI) coordinates of that node, along with the network to which each node belongs, as found in Power et al. [2011]. In addition, the hubness score (component score on the first principal component derived from the four centrality metrics) is displayed for each node

Table SV. Coordinates and descriptions of top 10 hub nodes for weighted‐average approach at top 20% density

Table SVI. Comparison of Original and Regressed Whole‐Brain Network Estimates. Table comparing original and task‐event regressed (see Materials and Methods) whole‐brain graph‐metrics computed at the top 20% proportional threshold. p‐Values of the difference between the resting‐state and the regressed task scans reported in parentheses. The regression of task events had minimal effects on the whole‐brain network estimates, but did produce slight average increases in global efficiency and decreases in clustering and between‐versus‐within module connections