Abstract
Math‐gifted subjects are characterized by above‐age performance in intelligence tests, exceptional creativity, and high task commitment. Neuroimaging studies reveal enhanced functional brain organization and white matter microstructure in the frontoparietal executive network of math‐gifted individuals. However, the cortical morphometry of these subjects remains largely unknown. The main goal of this study was to compare the cortical morphometry of math‐gifted adolescents with that of an age‐ and IQ‐matched control group. We used surface‐based methods to perform a vertex‐wise analysis of cortical thickness and surface area. Our results show that math‐gifted adolescents present a thinner cortex and a larger surface area in key regions of the frontoparietal and default mode networks, which are involved in executive processing and creative thinking, respectively. The combination of reduced cortical thickness and larger surface area suggests above‐age neural maturation of these networks in math‐gifted individuals. Hum Brain Mapp 37:1893–1902, 2016. © 2016 Wiley Periodicals, Inc.
Keywords: area, cortex, default mode, frontoparietal, math‐giftedness, thickness
INTRODUCTION
In the last decade, new insights from brain imaging techniques have revealed a potential association between individual differences in intelligence (e.g., IQ, g‐factor) and brain functioning and cortical morphometry [Jung and Haier, 2007]. In parallel, neuroimaging researchers have been trying to identify the neural bases that underlie giftedness. In broad terms, giftedness is a special type of intelligence that takes the form not only of higher IQ and enhanced executive functioning but also of exceptional creativity (such as the production of novel and useful ideas) and higher motivation in specific traits [Kalbfleisch, 2004; Kießwetter, 1985; Renzulli, 1978, 1998; Sternberg, 2010; Sternberg and Davidson, 2005]. Regarding the motivation (called also task commitment by Renzulli), gifted subjects show high levels of interest, fascination, perseverance, and dedicated practice in a particular problem or area of study. When these abilities are applied to mathematical thinking, subjects are referred to as “math‐gifted.”
Task‐based functional magnetic resonance imaging (fMRI) and diffusion tensor imaging (DTI) data support the existence of special characteristics of the frontoparietal executive network (FPN) in math‐gifted individuals [Desco et al., 2011; Hoppe et al., 2012; Lee et al., 2006; Navas‐Sanchez et al., 2014; O'Boyle, 2008; O'Boyle et al., 2005; Prescott et al., 2010]. For instance, task‐based fMRI studies on executive functioning and fluid reasoning detected enhanced functional bilateralism in math‐gifted adolescents in the dorsolateral prefrontal cortex, parietal cortex (including the superior and inferior parietal regions), and anterior cingulate cortex [Desco et al., 2011; O'Boyle et al., 2005; Prescott et al., 2010]. Similarly, a recent DTI study in math‐gifted subjects [Navas‐Sanchez et al., 2014] reported heightened connectivity between the left and right hemispheres, as well as enhanced intrahemispheric white matter connectivity between the frontal and parietal cortices.
In the same way, some neuroimaging studies showed recently the involvement of the default mode network (DMN) in the creative cognition [Benedek et al., 2014; Ellamil et al., 2012; Gonen‐Yaacovi et al., 2013; Jung et al., 2013; Takeuchi et al., 2011a; Wei et al., 2014]. Creativity is related with the unconscious knowledge and with an adaptive problem solving (i.e., often inductive as opposed to deductive reasoning). Creative thought appears to depend, at least in part, on disinhibitory neuronal processes within the DMN but also with cognitive control networks [Jung et al., 2013].
Several reports indicate that gifted individuals perform above their age in cognitive tests, thus suggesting a higher level of intellectual maturation than their same‐age peers [Alexander et al., 1996; Geake, 2008; Gross, 2004; O'Boyle and Benbow, 1990]. This cognitive precocity, especially in terms of IQ and working memory, has been associated with particular neural features that are compatible with a higher level of maturation in the frontoparietal executive network [Alexander et al., 1996; Geake, 2008]. Importantly, some characteristics of the brain cortex, particularly cortical thickness or surface area, have been shown to be a reliable correlates of cognitive abilities, as well as a good indicator of neural maturity. On one hand, studies in nongifted subjects have reported the existence of relationships between measurements of cortical thickness and surface area and high‐level neurocognitive abilities such as IQ, g‐factor, executive functioning, fluid reasoning, or creativity [Burzynska et al., 2012; Colom et al., 2013; Fjell et al., 2006, 2015; Jung et al., 2010; Karama et al., 2011; Luders et al., 2009; Narr et al., 2007; Schnack et al., 2015; Shaw et al., 2006; Skranes et al., 2013; Tamnes et al., 2010b). Broadly speaking, these associations indicate that higher cognitive ability corresponds to lower cortical thickness and larger surface area. Furthermore, a previous VBM study described larger cortical volume in frontoparietal regions in adult mathematicians highlighting the association between the exceptionally enlarged inferior parietal lobules and outstanding creativity in mathematic thinking [Aydin et al., 2007]. On the other hand, developmental studies suggested that during adolescence, cortical thickness decreases and surface area increases [Aleman‐Gomez et al., 2013]. Furthermore, cross‐sectional and longitudinal studies report different patterns of cortical maturation as a function of subject IQ [Schnack et al., 2015; Shaw et al., 2006]. However, to our knowledge, the possible existence of cortical features that are specific to math‐gifted children has not been explored.
In this study, we aim to describe the morphometric characteristics of the cortex of mathematically gifted adolescents. To ensure that IQ effects are not confounded with those of the construct of “giftedness,” the control subjects included in the study were group‐matched for overall IQ level with the math‐gifted subjects.
Based on prior studies of math‐giftedness and previous data from average math ability subjects, we hypothesized that the cognitive precocity of giftedness would entail cortical features that are compatible with above‐age brain maturation. More specifically, we predict that these differences would affect regions of the frontoparietal executive network. In addition, since creativity skills are considered a central characteristic of giftedness [Geake, 2008; Navas‐Sanchez et al., 2014; Renzulli, 1978, 1998; Sternberg and Davidson, 2005] and recent literature suggests that individual differences in creativity are associated with key nodes of the default mode network (DMN) [Jung et al., 2013; Takeuchi et al., 2011a), we also expect above‐age morphometric characteristics—such as thinner cortex and larger surface area—in the DMN of math‐gifted individuals.
METHODS
Sample Description
The sample recruited for the study included 62 right‐handed adolescents (aged between 11 and 15 years), of whom 13 were math‐gifted subjects (5 females) and 49 were controls (22 females). From the 49 controls, we selected a subsample of 21 subjects (6 females) who were group‐matched in age and IQ with the math‐gifted sample. In addition, 4 controls were excluded owing to movement during image acquisition; therefore, the final sample included 17 control subjects (6 females). All subjects had between 5 and 9 years of schooling in the Spanish education system. Subjects meeting the criteria for neurological disease, psychiatric disease, presence of MRI‐incompatible bioimplants, or medical conditions were not included in the study. Table 1 shows the demographic characteristics of the sample.
Table 1.
Median, mean, and standard deviation (SD) of demographic variables and global brain morphometric variables (LH, left hemisphere; RH, right hemisphere)
| Math‐gifted (n = 13; 5 females) | High‐IQ controls (n = 17; 6 females) | p value | Cohen's d | 95% IC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Median | Mean | SD | Median | Mean | SD | Lower | Upper | |||
| Age (years) | 13 | 13.23 | 0.7 | 13 | 13.15 | 1.2 | 1 | 0.08 | ||
| Sex (females) | 38% | 35% | 0.858 | |||||||
| Age range (years) [min–max] | [12–14] | [11–15] | ||||||||
| Estimated full‐scale IQ | 129 | 130 | 10.7 | 125 | 123 | 8.4 | 0.123 | 0.68 | −0.67 | 13.67 |
| IQ range [min–max] | [112–149] | [112–137] | ||||||||
| Verbal IQ | 120 | 125.08 | 12.1 | 114 | 120.35 | 17.5 | 0.385 | 0.31 | −6.92 | 16.38 |
| Performance IQ | 131 | 128.85 | 12.1 | 123 | 121.18 | 14.1 | 0.94 | 0.58 | −2.36 | 17.70 |
| Intracranial volume (cm3) | 1485.12 | 98.32 | 1392.29 | 115.76 | 0.035 | 0.85 | 10.85 | 174.81 | ||
| Total grey matter volume (cm3) | 592.17 | 42.42 | 570.58 | 45.41 | 0.245 | 0.49 | −11.73 | 54.91 | ||
| LH grey matter volume (cm3) | 297.44 | 20.65 | 286.70 | 23.53 | 0.213 | 0.48 | −6.12 | 27.60 | ||
| RH grey matter volume (cm3) | 294.73 | 22.03 | 283.88 | 22.15 | 0.213 | 0.49 | −5.83 | 27.53 | ||
| Total white matter volume (cm3) | 456.89 | 34.56 | 424.37 | 39.03 | 0.031 | 0.87 | 4.46 | 60.58 | ||
| LH white matter volume (cm3) | 225.30 | 17.32 | 210.62 | 19.89 | 0.065 | 0.78 | 0.47 | 28.89 | ||
| RH white matter volume (cm3) | 231.59 | 17.50 | 213.75 | 19.25 | 0.014 | 0.96 | 3.86 | 31.82 | ||
| Total cortical volume (cm3) | 531.28 | 39.69 | 513.30 | 41.74 | 0.245 | 0.44 | −12.87 | 48.83 | ||
| LH cortical volume (cm3) | 265.75 | 19.24 | 256.89 | 21.48 | 0.263 | 0.43 | −6.65 | 24.37 | ||
| RH cortical volume (cm3) | 265.52 | 20.75 | 256.41 | 20.48 | 0.263 | 0.44 | −6.43 | 24.65 | ||
| Total surface area (cm2) | 183.94 | 13.10 | 172.13 | 15.20 | 0.031 | 0.82 | 0.99 | 22.63 | ||
| LH surface area (cm2) | 91.63 | 6.71 | 86.02 | 7.98 | 0.065 | 0.75 | −0.02 | 11.24 | ||
| RH surface area (cm2) | 92.31 | 6.47 | 86.12 | 7.29 | 0.015 | 0.89 | 0.94 | 11.44 | ||
| Mean cortical thickness (mm) | 2.579 | 0.082 | 2.652 | 0.078 | 0.039 | 0.92 | −0.13 | −0.01 | ||
| LH mean cortical thickness (mm) | 2.580 | 0.080 | 2.659 | 0.078 | 0.010 | 1.00 | −0.14 | −0.02 | ||
| RH mean cortical thickness (mm) | 2.579 | 0.087 | 2.645 | 0.081 | 0.072 | 0.79 | −0.13 | 0.00 | ||
The global measurements of brain morphometry—intracranial volume, total grey matter volume (including cortex and basal ganglia), total cortex volume, total surface area, and whole brain mean thickness—were obtained with VBM8 and FreeSurfer. Significant p values controlled by FDR correction (q < 0.05) and confidence intervals (95% CI) are shown in bold type.
The math‐gifted adolescents were recruited form the Stimulus of Mathematical Talent Program (ESTALMAT; http://www.uam.es/proyectosinv/estalmat/) of the Spanish Royal Academy of Mathematical, Physical, and Natural Sciences in Madrid. Candidates for the ESTALMAT program are children who are particularly good at mathematics and willing to participate in the program and are recommended by teachers. The subjects underwent a screening process consisting of a personal interview and math‐related tests.
Those who passed this preliminary assessment underwent a second examination based on a variety of specific tests proposed by Kießwetter [1985] according to the identification and assessment of “mathematical giftedness” from Renzulli [1978]. The objective of these tests is to detect complex mathematical abilities that could be categorized as cognitive, motivational, and creative. Specifically, the tests assess visuospatial thinking, intuition, creativity, abstraction, manipulation, and ability to manage thoughts as follows: (1) organizing materials; (2) recognizing patterns or rules; (3) changing the representation of the problem and recognizing patterns and rules in a new area; (4) comprehending and working with highly complex structures; (5) reversing and inverting processes; and (6) finding related problems [Heller et al., 2000]. Test answers were examined by mathematicians who considered not only the correctness of the answers but also the argumentation followed to achieve the solution. The tests chosen were as original as possible, in such a way that previous training would not imply a clear advantage. In contrast with other standardized measures such as SAT‐Math (Scholastic Assessment Test, Mathematics Section), ESTALMAT emphasizes problem solving by creative thinking, rather than using concepts and previous expertise gained at school [Navas‐Sanchez et al., 2014]. This procedure was used in previous works [Desco et al., 2011; Navas‐Sanchez et al., 2014] and followed similar criteria to that used in some other articles about math‐giftedness [Zhang et al., 2014, 2015].
The control group was selected based on their age and IQ and academic levels. IQ was estimated using the Vocabulary, Information, and Block Design subtests from the Spanish version of the Wechsler Intelligence Scale for Children—Revised. These tests show good correspondence with full‐scale IQ [Ringe et al., 2002; Silverstein, 1985] and are commonly used in the literature. The cognitive assessment was performed by a child neuropsychologist and a child psychiatrist, who also analyzed the subjects' school records.
This study was approved by the Hospital Ethics and Clinical Research Boards. Written informed consent was obtained from both subjects and their parents before the study was performed.
Magnetic Resonance Imaging Acquisition
Data were acquired with a Philips Intera 1.5 T MRI scanner (Philips Medical Systems, Best, The Netherlands). The details of the protocol were as follows: high‐resolution structural image T1‐weighted gradient‐echo; repetition time [TR] = 25 ms; echo time [TE] = 9.2 ms; field of view [FOV] = 256 × 256 × 175; flip angle = 30°; voxel size = 1 × 1 × 1 mm3.
MRI Data Preprocessing
First, MRI scans were skull‐stripped and tissue‐segmented with SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK; available at: http://www.fil.ion.ucl.ac.uk/spm) using the VBM8 toolbox (available at: http://dbm.neuro.uni-jena.de/vbm). All the images had to pass an exhaustive quality control following the considerations recently appointed by [Ducharme et al., 2016]. All the images were visually inspected and the skull was manually removed if necessary by an experienced neuroradiologist blind to the groups. Less than 20% of images required manual correction. The reconstructed surfaces were also checked and none of those presented any topological errors.
Second, we performed a vertex‐wise analysis using surface‐based methods to account for group differences in whole‐brain cortical thickness and surface area. Briefly, we processed the structural images with the standard FreeSurfer pipeline (available at: http://www.surfer.nmr.mgh.harvard.edu, version 5.3), which constructs models of the cortical interfaces (white–grey matter and CSF–grey matter) for all the subjects in the native anatomical space [Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 1999]. Before the statistical analyses, cortical thickness and surface area maps were normalized to a standard space (MNI space) and smoothed using a Gaussian filter with a full‐width at half‐maximum of 15 mm.
Statistical Analysis
Group differences in whole‐brain measurements (grey matter volume, intracranial volume, white matter volume, mean thickness, surface area, and cortex volume) were based on nonparametric statistical methods, namely Mann–Whitney U test. Standardized effect sizes and confidence intervals of the differences (95% CI) were also reported. Gender differences were compared using Pearson's chi‐square test. The results of the whole‐brain measurements were controlled by the False Discovery Rate, FDR (q < 0.05).
A vertex‐wise statistical analysis was carried out separately for both the left and right hemispheres. The statistical significance in vertex‐wise data (cortical thickness and surface area) was assessed using a two‐tailed two‐sample t test. Standardized effect sizes (Cohen's d) were also calculated in the vertex‐wise maps.
Correction for multiple comparisons used the cluster‐wise probability method (CWP) [Hagler et al., 2006]. A total of 10,000 Monte‐Carlo random permutations were used to obtain a CWP value <0.05.
Additionally, to ensure that group differences in age, gender, and IQ were not confounded, we repeated group comparisons including “age,” “gender,” and “IQ” as covariates. Furthermore, to exclude the potential effect of cortical volume, we also performed another ANCOVA with cortex volume as a covariate. The output of these models is reported in the Supporting Information.
RESULTS
Global Measurements
Compared with controls, math‐gifted subjects presented larger intracranial volume (d = 0.83), lower whole‐brain mean cortical thickness (d = 0.91), larger white matter volumes (d = 1.22), and larger whole‐brain surface area (d = 0.84). There were no significant differences between math‐gifted subjects and controls in total cortical volume (Table 1).
Vertex‐Wise Analysis: Group Differences in Cortical Thickness
Vertex‐wise cortical thickness analysis revealed thinning in the bilateral superior frontal gyrus, left medial prefrontal cortex, anterior cingulate cortex, left precuneus, left medial prefrontal cortex (mPFC), left orbitofrontal cortex, and right superior parietal cortex (Table 2 and Fig. 1‐1) in math‐gifted individuals. In addition, the Cohen's d maps (Fig. 1‐1) of group differences revealed a large effect size for the right medial prefrontal cortex, the lateral orbitofrontal cortex, and the supramarginal gyrus (d > 0.8). Compared with math‐gifted subjects, the controls did not show a significant reduction in cortical thickness.
Table 2.
Vertex‐wise analysis of cortical thickness and surface area
| Measurement | Anatomical region | Side | Cluster size (mm2) | X | Y | Z | CWP |
|---|---|---|---|---|---|---|---|
| Lower cortical thickness | |||||||
| Superior parietal | RH | 1339.62 | 17.6 | −68.8 | 45.2 | 0.0315 | |
| Superior frontal | RH | 3901.20 | 7.5 | 6.6 | 65.6 | 0.0001 | |
| Pars orbitalis | LH | 2994.61 | −44.1 | 41.3 | −11.4 | 0.0001 | |
| Superior frontal | LH | 4543.72 | −5.9 | −2.7 | 59.8 | 0.0001 | |
| Precuneus | LH | 2266.05 | −11.6 | −62.6 | 21.8 | 0.0007 | |
| Larger surface area | |||||||
| Superior frontal | RH | 3955.97 | 21.7 | 28 | 36.3 | 0.0001 | |
| Lingual | RH | 4188.24 | 6.6 | −79.6 | −4 | 0.0001 | |
| Superior frontal | LH | 3984.19 | −21.9 | 9.9 | 48.7 | 0.0001 | |
| Inferior parietal | LH | 2833.52 | −43.6 | −75.8 | 14.5 | 0.0022 | |
The anatomical coordinates indicate the location where math‐gifted subjects showed significantly thinner cortex or significantly larger surface area in the corrected clusters (LH, left hemisphere; RH, right hemisphere). CWP: cluster‐wise probability.
Figure 1.
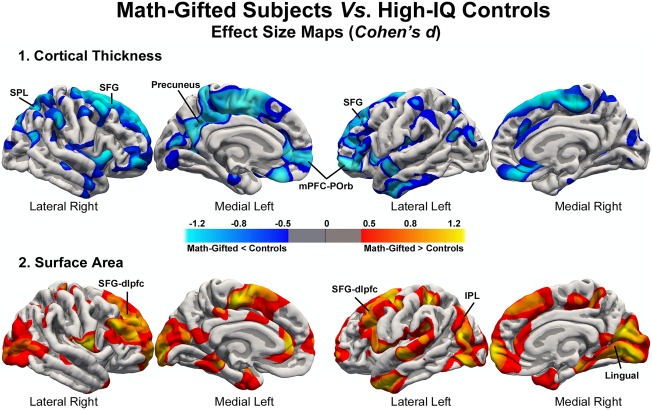
Vertex‐wise analysis. Group differences in (1) cortical thickness and (2) surface area. Thinner cortex in math‐gifted adolescents is represented in blue, and larger surface area than high‐IQ controls appears in warm colors. Math‐gifted subjects did not present regions with significantly thicker cortex or lower surface area than controls. The Cohen's d maps are thresholded at d > 0.5 (medium effect, represented with dark blue or red), and d > 0.8 (high effect, represented in light blue or yellow). The clusters that survived the multiple comparisons correction (CWP < 0.05) were identified as superior frontal gyrus (SFG), superior frontal gyrus‐dorsolateral prefrontal cortex (SFG‐dlpfc), superior parietal lobule (SPL), inferior parietal lobule (IPL), medial prefrontal cortex‐pars orbitalis (mPFC‐POrb), and lingual. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Vertex‐Wise Analysis: Group Differences in Surface Area
Vertex‐wise analysis of surface area revealed that the surface of the left and right frontal lobes was larger for math‐gifted subjects, particularly in the left caudal and the right rostral middle frontal gyri, which are included in the dorsolateral prefrontal cortex. Moreover, the surface area of the left lateral occipital and inferior parietal lobes and of the right lingual gyrus was significantly larger in math‐gifted subjects (Table 2 and Fig. 1‐2). The Cohen's d map indicates that the area of the bilateral parahippocampal gyrus, right mPFC, and left anterior cingulate cortex is significantly larger in math‐gifted subjects (Fig. 1‐2).
The inclusion of covariates such as sex, IQ, and total cortical volume did not noticeably alter the findings for cortical thickness or surface area (Supporting Information). In other words, the significant clusters observed in the t‐test are the same as that obtained in the ANCOVA in which we include IQ and Gender, and the model is more parsimonious with a great number of degrees of freedom. Indeed, the results with “age” as a covariate in the model were omitted because there is a lack of significance of the “age” covariate probably due to the age range spanned. Only when including “Total Cortex Volume” as covariate in the surface area data, any cluster survived the CWP correction. However, the effect size (Cohen's d) showed between‐group differences in the same regions than the t‐test analysis.
DISCUSSION
The relationship between cortical morphometry and intellectual abilities such as general intelligence or creativity has been widely described in the literature; however, to our knowledge, the relationship between cortical morphometry and math‐giftedness has not yet been explored. The aim of this study was to identify potential morphometric differences, in particular cortical thickness and surface area, between math‐gifted adolescents and controls using surface‐based methodologies. Biologically, cortical thickness and surface area should be considered as independent measurements. Cortical thickness is more related to the number of cells (the amount of neurons or glial cells) and capillary support, whereas the surface area is related to the number and spacing of minicolumnar units of cells [Feczko et al., 2009; Hill et al., 2010; Mountcastle, 1997; Panizzon et al., 2009; Rakic, 1988]. The difference in the cortical features (cortical thickness and area) between math‐gifted and controls could explain the differences in intelligence and creativity. We found that the cortex of gifted subjects was thinner in the superior dorsolateral prefrontal and superior parietal regions and that the surface area was larger in the superior and middle dorsolateral prefrontal cortex, which are key regions of the frontoparietal executive network (FPN). We also found the cortex to be thinner in the mPFC and precuneus and the surface area to be larger in the medial temporal lobes and the right mPFC, which are key nodes of the DMN.
Neural Development in Math‐Giftedness
One of the main features that characterize gifted individuals is that they perform above their age in cognitive tests (mainly IQ) and creativity measurements, thus demonstrating a higher level of cognitive maturation than their same‐age peers [Geake, 2008; Gross, 2004]. Our findings of a thinner cortex and larger surface than in same‐age controls suggest that this cognitive precocity may be the outcome of above‐age neural development.
Several studies have suggested the existence of cortical thinning due to synaptic pruning [Changeux and Danchin, 1976; Huttenlocher and Dabholkar, 1997; Paus, 2005; Petanjek et al., 2011] and neuropil myelination [Gogtay and Thompson, 2010; Sowell et al., 2004] during adolescence. Furthermore, some cross‐sectional studies also suggested that a thinner cortex at a given age might reflect earlier cortical maturation [Tamnes et al., 2011, 2010a]. According to these data, our finding of decreased whole‐brain cortical thickness in gifted individuals could indicate a more mature brain in terms of synaptic pruning and myelination. Our data also indicate that math‐gifted adolescents show larger surface area and white matter volume. According to the “Balloon Model” hypothesis [Seldon, 2005], this finding may reflect a more advanced level of myelination. This model proposes a neuroanatomical description linking human white matter growth and volume to the thickness of the overlying cortex, and justifies the inverse relationship between cortical thickness and surface area. Therefore, we can speculate that the exceptional cognitive skills of math‐gifted subjects might be linked to above‐age neural development, as reflected by thinner cortex and highly expanded surface area.
Between‐Group Differences in Cortical Morphometry: Frontoparietal and Default Mode Networks
Morphometric differences are localized in regions belonging to frontoparietal and default mode networks. The maturation of these networks during childhood and adulthood underlies the development of higher‐level cognitive functions, such as executive functioning and creative thinking, which are often exceptional in gifted individuals [de Bie et al., 2012; Hoff et al., 2013].
The frontoparietal network plays a key role in intelligence as it is critical for executive control by keeping on‐line working memory representations necessary for problem solving, decision‐making, and other goal‐directed processes [Baddeley, 2003; Jung and Haier, 2007]. Our findings complement previous data showing special characteristics of the frontoparietal executive network in terms of functionality [Desco et al., 2011; Hoppe et al., 2012; Lee et al., 2006; O'Boyle, 2008; O'Boyle et al., 2005; Prescott et al., 2010] and anatomical connectivity [Navas‐Sanchez et al., 2014]. Although the FPN has been extensively related to individual differences in general intelligence [Jung and Haier, 2007], it is unlikely that the implication of the FPN in giftedness could be explained merely in terms of IQ level since the control group was matched for overall IQ.
According to theoretical definitions of giftedness, gifted individuals show not only higher IQ and enhanced executive functioning but also exceptional creativity and higher task motivation [Heller et al., 2000; Kalbfleisch, 1985, 2004; Renzulli, 1978, 1998; Sternberg and Davidson, 2005]. In recent years, an increasing number of functional and structural neuroimaging studies point to the implication of the DMN in creative thinking [Benedek et al., 2014; Ellamil et al., 2012; Gonen‐Yaacovi et al., 2013; Jung et al., 2013; Takeuchi et al., 2011a; Wei et al., 2014]. Consistently, our findings suggest that giftedness is associated with atypical cortical characteristics in regions of the DMN. In particular, we found that math‐gifted subjects present thinner cortex in the precuneus and the mPFC and anterior cingulate cortex (ACC), as well as larger surface area in the medial temporal lobes bilaterally (including the parahippocampal gyrus) and the right mPFC‐ACC, areas that have been directly associated with creative thinking [Jung et al., 2013]. Notwithstanding, some authors suggest that creativity does not rely exclusively on the DMN but also on the interplay between DMN regions and other areas such as the dorsolateral prefrontal cortex, the inferior parietal cortex, and the orbitofrontal cortex [Aydin et al., 2007; Jung et al., 2010; Shamay‐Tsoory et al., 2011; Takeuchi et al., 2010, 2011b), which we also found to be atypical in our sample of gifted subjects. In keeping with previous theorizing, the mPFC and ACC regions have been proposed as key regions for mathematical giftedness [O'Boyle et al., 2005; Prescott et al., 2010]. And the aforementioned enhanced functional connectivity among brain regions in math‐gifted subjects could be orchestrated by the ACC being a hub not only for motivation or attention but also for information processing and creative cognition [Jung, 2014].
Additionally, we found surface area to be greater in the bilateral visual cortex of math‐gifted subjects than that of controls. The visual cortex has been extensively implicated in attentional functions as well as in visual imagery and visuospatial processing [Jehee et al., 2011; Leshikar et al., 2012; Moradi et al., 2012]. fMRI reports in math‐gifted subjects have shown activations in visual areas while performing executive functioning and fluid reasoning tasks [Desco et al., 2011; Lee et al., 2006; O'Boyle et al., 2005]. Similarly, in our previous DTI study, we also found that math‐gifted subjects have a higher fractional anisotropy (FA) in the parieto‐occipital and fronto‐occipital tracts, thus suggesting greater abilities in visuospatial stream processing and possibly enriched mental images associated with visuospatial working memory [Navas‐Sanchez et al., 2014].
Finally, we believe that the integration of morphological, functional, and DTI data from math‐gifted individuals is key to understanding math‐giftedness. We previously characterized the current math‐gifted sample in terms of functionality—while performing executive functioning and fluid reasoning tasks [Desco et al., 2011]—and structural connectivity [Navas‐Sanchez et al., 2014]. In this study, we describe their morphometric features.
Combining our findings, math‐gifted subjects show greater bilateral activation in dorsal attentional and FPN networks [Desco et al., 2011], enhanced structural connectivity between frontoparietal and fronto‐striatal major tracts [Navas‐Sanchez et al., 2014], and larger surface area accompanied by thinner cortex in frontoparietal regions.
Previous studies on morphometric and functional features suggest the presence of a negative relationship between cortical thickness and functional activity [Lu et al., 2009; Nunez et al., 2011]. Although the neural mechanisms underlying this negative association are unknown, it has been suggested that the synaptic pruning leading to cortical thinning during adolescence could also increase the selectivity and effectiveness of the neural structure, thus producing stronger functional activations [Lu et al., 2009; Nunez et al., 2011]. Furthermore, Lu et al. [2009] proposed that higher skill level, such as that observed in math‐gifted individuals, is associated with a stronger activation pattern in frontoparietal and attentional networks. These activations also corresponded to more “mature” morphology in these regions (thinner cortex), even after controlling for IQ [Lu et al., 2009; Nunez et al., 2011]. Moreover, white matter microstructure and cortical properties are also negatively associated with maturational processes [Giorgio et al., 2008; Tamnes et al., 2010a]. It has been proposed that age‐related changes in cortical thickness and white matter microstructure may be driven, in part, by a common biological mechanism, presumed to be associated with changes in cerebral myelination [Kochunov et al., 2011].
Math‐gifted subjects are qualitatively and quantitatively different, not only in terms of brain activation and white matter organization but also in terms of cortical morphometry. From a transversal imaging perspective, our studies depict a math‐gifted brain characterized by exceptional and above‐age structural properties in the frontoparietal circuit.
Our study presents several limitations. First, the cross‐sectional design prevents us from assessing the cognitive and neural maturation of the subjects over time. Of note, the term “precocity,” as used in this manuscript, refers merely to the presence of cognitive and neural features typically found in older subjects.
Furthermore, the sample size is relatively small. As expected, it was difficult to recruit larger samples since we are studying an exceptional form of intelligence that is extremely rare in the population. However, our sample was very carefully selected, and comprised math‐gifted adolescents and nongifted controls, all right‐handed, with balanced gender effects, who were all right‐handed, balanced for gender, of the same age and importantly, within an approximately similar IQ range.
Our findings are also limited by the cognitive characterization of the two groups. Recruitment of math‐gifted subjects was based on their admission to the ESTALMAT program although controls were not evaluated and excluded by the same ESTALMAT program. Because controls did not undertake the same selection test battery, we cannot positively rule out the possibility that a given control individual was in actuality, math‐gifted; however, given the low proportion (<5%) of math‐gifted subjects in the population, we can realistically assume that our controls were not gifted.
Most importantly, the effect of possible misclassification of controls weakens our hypothesis since the statistical effect of giftedness would appear diminished. Nevertheless, our findings remain reasonably robust despite this potential drawback.
CONCLUSIONS
In summary, math‐gifted adolescents showed special morphological properties in regions of the frontoparietal and default mode networks in charge of executive processing and creative thinking, respectively. The combination of reduced cortical thickness and larger surface area in these regions suggests the presence of above‐age neural maturation in gifted individuals.
Supporting information
Supporting Information
ACKNOWLEDGMENTS
The authors wish to express their sincere appreciation of the invaluable contribution of the late Dr Santiago Reig to this study.
The authors do not have conflicts of interest to declare.
REFERENCES
- Aleman‐Gomez Y, Janssen J, Schnack H, Balaban E, Pina‐Camacho L, Alfaro‐Almagro F, Castro‐Fornieles J, Otero S, Baeza I, Moreno D, Bargallo N, Parellada M, Arango C, Desco M (2013): The human cerebral cortex flattens during adolescence. J Neurosci 33:15004–15010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander JE, O'Boyle MW, Benbow CP (1996): Developmentally advanced EEG alpha power in gifted male and female adolescents. Int J Psychophysiol 23:25–31. [DOI] [PubMed] [Google Scholar]
- Aydin K, Ucar A, Oguz KK, Okur OO, Agayev A, Unal Z, Yilmaz S, Ozturk C (2007): Increased gray matter density in the parietal cortex of mathematicians: a voxel‐based morphometry study. AJNR Am J Neuroradiol 28:1859–1864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley A (2003): Working memory: looking back and looking forward. Nat Rev Neurosci 4:829–839. [DOI] [PubMed] [Google Scholar]
- Benedek M, Beaty R, Jauk E, Koschutnig K, Fink A, Silvia PJ, Dunst B, Neubauer AC (2014): Creating metaphors: the neural basis of figurative language production. Neuroimage 90:99–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burzynska AZ, Nagel IE, Preuschhof C, Gluth S, Backman L, Li SC, Lindenberger U, Heekeren HR (2012): Cortical thickness is linked to executive functioning in adulthood and aging. Hum Brain Mapp 33:1607–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colom R, Burgaleta M, Roman FJ, Karama S, Alvarez‐Linera J, Abad FJ, Martinez K, Quiroga MA, Haier RJ (2013): Neuroanatomic overlap between intelligence and cognitive factors: morphometry methods provide support for the key role of the frontal lobes. Neuroimage 72:143–152. [DOI] [PubMed] [Google Scholar]
- Changeux JP, Danchin A (1976): Selective stabilisation of developing synapses as a mechanism for the specification of neuronal networks. Nature 264:705–712. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI (1999): Cortical surface‐based analysis. I. Segmentation and surface reconstruction. Neuroimage 9:179–194. [DOI] [PubMed] [Google Scholar]
- de Bie HM, Boersma M, Adriaanse S, Veltman DJ, Wink AM, Roosendaal SD, Barkhof F, Stam CJ, Oostrom KJ, Delemarre‐van de Waal HA, Sanz‐Arigita EJ (2012): Resting‐state networks in awake five‐ to eight‐year old children. Hum Brain Mapp 33:1189–1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desco M, Navas‐Sanchez FJ, Sanchez‐Gonzalez J, Reig S, Robles O, Franco C, Guzman‐De‐Villoria JA, Garcia‐Barreno P, Arango C (2011): Mathematically gifted adolescents use more extensive and more bilateral areas of the fronto‐parietal network than controls during executive functioning and fluid reasoning tasks. Neuroimage 57:281–292. [DOI] [PubMed] [Google Scholar]
- Ducharme S, Albaugh MD, Nguyen TV, Hudziak JJ, Mateos‐Pérez JM, Labbe A, Evans AC, Karama S (2016): Trajectories of cortical thickness maturation in normal brain development — The importance of quality control procedures. NeuroImage 125:267–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellamil M, Dobson C, Beeman M, Christoff K (2012): Evaluative and generative modes of thought during the creative process. Neuroimage 59:1783–1794. [DOI] [PubMed] [Google Scholar]
- Feczko E, Augustinack JC, Fischl B, Dickerson BC (2009): An MRI‐based method for measuring volume, thickness and surface area of entorhinal, perirhinal, and posterior parahippocampal cortex. Neurobiol Aging 30:420–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM (2000): Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA 97:11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM (1999): Cortical surface‐based analysis. II: Inflation, flattening, and a surface‐based coordinate system. Neuroimage 9:195–207. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Walhovd KB, Reinvang I, Lundervold A, Salat D, Quinn BT, Fischl B, Dale AM (2006): Selective increase of cortical thickness in high‐performing elderly–structural indices of optimal cognitive aging. Neuroimage 29:984–994. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Westlye LT, Amlien I, Tamnes CK, Grydeland H, Engvig A, Espeseth T, Reinvang I, Lundervold AJ, Lundervold A, Walhovd KB (2015): High‐expanding cortical regions in human development and evolution are related to higher intellectual abilities. Cereb Cortex 25:26–34. [DOI] [PubMed] [Google Scholar]
- Geake, J.G. (2008): The neurobiology of giftedness. In: Wystąpienie na konferencji 10th Asia‐Pacific Conference on Giftedness, Singapur.
- Giorgio A, Watkins KE, Douaud G, James AC, James S, De Stefano N, Matthews PM, Smith SM, Johansen‐Berg H (2008): Changes in white matter microstructure during adolescence. NeuroImage 39:52–61. [DOI] [PubMed] [Google Scholar]
- Gogtay N, Thompson PM (2010): Mapping gray matter development: implications for typical development and vulnerability to psychopathology. Brain Cogn 72:6–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonen‐Yaacovi G, de Souza LC, Levy R, Urbanski M, Josse G, Volle E (2013): Rostral and caudal prefrontal contribution to creativity: a meta‐analysis of functional imaging data. Front Hum Neurosci 7:465 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross MU (2004): Exceptionally Gifted Children. Psychology Press. [Google Scholar]
- Hagler DJJ, Saygin AP, Sereno MI (2006): Smoothing and cluster thresholding for cortical surface‐based group analysis of fMRI data. Neuroimage 33:1093–1103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heller KA, Mönks FJ, Subotnik R, Sternberg RJ (2000): International Handbook of Giftedness and Talent. Elsevier. [Google Scholar]
- Hill J, Inder T, Neil J, Dierker D, Harwell J, Van Essen D (2010): Similar patterns of cortical expansion during human development and evolution. Proc Natl Acad Sci USA 107:13135–13140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoff GE, Van den Heuvel MP, Benders MJ, Kersbergen KJ, De Vries LS (2013): On development of functional brain connectivity in the young brain. Front Hum Neurosci 7:650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoppe C, Fliessbach K, Stausberg S, Stojanovic J, Trautner P, Elger CE, Weber B (2012): A key role for experimental task performance: effects of math talent, gender and performance on the neural correlates of mental rotation. Brain Cogn 78:14–27. [DOI] [PubMed] [Google Scholar]
- Huttenlocher PR, Dabholkar AS (1997): Regional differences in synaptogenesis in human cerebral cortex. J Comp Neurol 387:167–178. [DOI] [PubMed] [Google Scholar]
- Jehee JF, Brady DK, Tong F (2011): Attention improves encoding of task‐relevant features in the human visual cortex. J Neurosci 31:8210–8219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung RE (2014): Evolution, creativity, intelligence, and madness: “Here Be Dragons”. Front Psychol 5:784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung RE, Haier RJ (2007): The Parieto‐Frontal Integration Theory (P‐FIT) of intelligence: converging neuroimaging evidence. Behav Brain Sci 30:135–154. discussion 154‐87. [DOI] [PubMed] [Google Scholar]
- Jung RE, Mead BS, Carrasco J, Flores RA (2013): The structure of creative cognition in the human brain. Front Hum Neurosci 7:330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung RE, Segall JM, Jeremy Bockholt H, Flores RA, Smith SM, Chavez RS, Haier RJ (2010): Neuroanatomy of creativity. Hum Brain Mapp 31:398–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalbfleisch ML (2004): Functional neural anatomy of talent. Anat Rec B New Anat 277:21–36. [DOI] [PubMed] [Google Scholar]
- Karama S, Colom R, Johnson W, Deary IJ, Haier R, Waber DP, Lepage C, Ganjavi H, Jung R, Evans AC (2011): Cortical thickness correlates of specific cognitive performance accounted for by the general factor of intelligence in healthy children aged 6 to 18. Neuroimage 55:1443–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kießwetter K (1985): Die Förderung von mathematisch besonders begabten und interessierten Schülern–ein bislang vernachlässigtes sonderpädagogisches Problem. Mathematisch‐Naturwissenschaftlicher Unterricht 38:300–306. [Google Scholar]
- Kochunov P, Glahn DC, Lancaster J, Thompson PM, Kochunov V, Rogers B, Fox P, Blangero J, Williamson DE (2011): Fractional anisotropy of cerebral white matter and thickness of cortical gray matter across the lifespan. NeuroImage 58:41–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KH, Choi YY, Gray JR, Cho SH, Chae JH, Lee S, Kim K (2006): Neural correlates of superior intelligence: stronger recruitment of posterior parietal cortex. Neuroimage 29:578–586. [DOI] [PubMed] [Google Scholar]
- Leshikar ED, Duarte A, Hertzog C (2012): Task‐selective memory effects for successfully implemented encoding strategies. PLoS One 7:e38160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu LH, Dapretto M, O'Hare ED, Kan E, McCourt ST, Thompson PM, Toga AW, Bookheimer SY, Sowell ER (2009): Relationships between brain activation and brain structure in normally developing children. Cereb Cortex 19:2595–2604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luders E, Gaser C, Narr KL, Toga AW (2009): Why sex matters: brain size independent differences in gray matter distributions between men and women. J Neurosci 29:14265–14270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moradi F, Buracas GT, Buxton RB (2012): Attention strongly increases oxygen metabolic response to stimulus in primary visual cortex. Neuroimage 59:601–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountcastle VB (1997): The columnar organization of the neocortex. Brain 120:701–722. [DOI] [PubMed] [Google Scholar]
- Narr KL, Woods RP, Thompson PM, Szeszko P, Robinson D, Dimtcheva T, Gurbani M, Toga AW, Bilder RM (2007): Relationships between IQ and regional cortical gray matter thickness in healthy adults. Cereb Cortex 17:2163–2171. [DOI] [PubMed] [Google Scholar]
- Navas‐Sanchez FJ, Aleman‐Gomez Y, Sanchez‐Gonzalez J, Guzman‐De‐Villoria JA, Franco C, Robles O, Arango C, Desco M (2014): White matter microstructure correlates of mathematical giftedness and intelligence quotient. Hum Brain Mapp 35:2619–2631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez SC, Dapretto M, Katzir T, Starr A, Bramen J, Kan E, Bookheimer S, Sowell ER (2011): fMRI of syntactic processing in typically developing children: structural correlates in the inferior frontal gyrus. Dev Cogn Neurosci 1:313–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Boyle MW (2008): Mathematically gifted children: Developmental brain characteristics and their prognosis for well‐being. Roeper Rev 30:181–186. [Google Scholar]
- O'Boyle MW, Benbow CP (1990): Enhanced right hemisphere involvement during cognitive processing may relate to intellectual precocity. Neuropsychologia 28:211–216. [DOI] [PubMed] [Google Scholar]
- O'Boyle MW, Cunnington R, Silk TJ, Vaughan D, Jackson G, Syngeniotis A, Egan GF (2005): Mathematically gifted male adolescents activate a unique brain network during mental rotation. Brain Res Cogn Brain Res 25:583–587. [DOI] [PubMed] [Google Scholar]
- Panizzon MS, Fennema‐Notestine C, Eyler LT, Jernigan TL, Prom‐Wormley E, Neale M, Jacobson K, Lyons MJ, Grant MD, Franz CE, Xian H, Tsuang M, Fischl B, Seidman L, Dale A, Kremen WS (2009): Distinct genetic influences on cortical surface area and cortical thickness. Cerebral Cortex 19:2728–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paus T (2005): Mapping brain maturation and cognitive development during adolescence. Trends Cogn Sci 9:60–68. [DOI] [PubMed] [Google Scholar]
- Petanjek Z, Judas M, Simic G, Rasin MR, Uylings HB, Rakic P, Kostovic I (2011): Extraordinary neoteny of synaptic spines in the human prefrontal cortex. Proc Natl Acad Sci USA 108:13281–13286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott J, Gavrilescu M, Cunnington R, O'Boyle MW, Egan GF (2010): Enhanced brain connectivity in math‐gifted adolescents: An fMRI study using mental rotation. Cogn Neurosci 1:277–288. [DOI] [PubMed] [Google Scholar]
- Rakic P (1988): Specification of cerebral cortical areas. Science 241:170–176. [DOI] [PubMed] [Google Scholar]
- Renzulli JS (1978): What makes giftedness? Reexamining a definition. Phi Delta Kappan 60:180. [Google Scholar]
- Renzulli JS (1998): The three‐ring conception of giftedness In: Baum SM, Reis SM, Maxfield LRE, editors. Nurturing the Gifts and Talents of Primary Grade Students. Mansfield Center, CT: Creative Learning Press. [Google Scholar]
- Ringe WK, Saine KC, Lacritz LH, Hynan LS, Cullum CM (2002): Dyadic short forms of the Wechsler Adult Intelligence Scale‐III. Assessment 9:254–260. [DOI] [PubMed] [Google Scholar]
- Schnack HG, van Haren NE, Brouwer RM, Evans A, Durston S, Boomsma DI, Kahn RS, Hulshoff Pol HE (2015): Changes in thickness and surface area of the human cortex and their relationship with intelligence. Cereb Cortex 25:1608–1617. [DOI] [PubMed] [Google Scholar]
- Seldon HL (2005): Does brain white matter growth expand the cortex like a balloon? Hypothesis and consequences. Laterality 10:81–95. [DOI] [PubMed] [Google Scholar]
- Shamay‐Tsoory SG, Adler N, Aharon‐Peretz J, Perry D, Mayseless N (2011): The origins of originality: the neural bases of creative thinking and originality. Neuropsychologia 49:178–185. [DOI] [PubMed] [Google Scholar]
- Shaw P, Greenstein D, Lerch J, Clasen L, Lenroot R, Gogtay N, Evans A, Rapoport J, Giedd J (2006): Intellectual ability and cortical development in children and adolescents. Nature 440:676–679. [DOI] [PubMed] [Google Scholar]
- Silverstein AB (1985): Two‐ and four‐subtest short forms of the WAIS‐R: a closer look at validity and reliability. J Clin Psychol 41:95–97. [DOI] [PubMed] [Google Scholar]
- Skranes J, Lohaugen GC, Martinussen M, Haberg A, Brubakk AM, Dale AM (2013): Cortical surface area and IQ in very‐low‐birth‐weight (VLBW) young adults. Cortex 49:2264–2271. [DOI] [PubMed] [Google Scholar]
- Sowell ER, Thompson PM, Leonard CM, Welcome SE, Kan E, Toga AW (2004): Longitudinal mapping of cortical thickness and brain growth in normal children. J Neurosci 24:8223–8231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternberg RJ (2010): Assessment of gifted students for identification purposes: New techniques for a new millennium. Learn Individ Diff 20:327–336. [Google Scholar]
- Sternberg RJ, Davidson JE (2005): Conceptions of Giftedness. Cambridge University Press. [Google Scholar]
- Takeuchi H, Taki Y, Hashizume H, Sassa Y, Nagase T, Nouchi R, Kawashima R (2011a): Failing to deactivate: the association between brain activity during a working memory task and creativity. Neuroimage 55:681–687. [DOI] [PubMed] [Google Scholar]
- Takeuchi H, Taki Y, Sassa Y, Hashizume H, Sekiguchi A, Fukushima A, Kawashima R (2010): Regional gray matter volume of dopaminergic system associate with creativity: evidence from voxel‐based morphometry. Neuroimage 51:578–585. [DOI] [PubMed] [Google Scholar]
- Takeuchi H, Taki Y, Sassa Y, Hashizume H, Sekiguchi A, Fukushima A, Kawashima R (2011b): Working memory training using mental calculation impacts regional gray matter of the frontal and parietal regions. PLoS One 6:e23175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamnes CK, Fjell AM, Ostby Y, Westlye LT, Due‐Tonnessen P, Bjornerud A, Walhovd KB (2011): The brain dynamics of intellectual development: waxing and waning white and gray matter. Neuropsychologia 49:3605–3611. [DOI] [PubMed] [Google Scholar]
- Tamnes CK, Ostby Y, Fjell AM, Westlye LT, Due‐Tonnessen P, Walhovd KB (2010a): Brain maturation in adolescence and young adulthood: regional age‐related changes in cortical thickness and white matter volume and microstructure. Cereb Cortex 20:534–548. [DOI] [PubMed] [Google Scholar]
- Tamnes CK, Ostby Y, Walhovd KB, Westlye LT, Due‐Tonnessen P, Fjell AM (2010b): Neuroanatomical correlates of executive functions in children and adolescents: a magnetic resonance imaging (MRI) study of cortical thickness. Neuropsychologia 48:2496–2508. [DOI] [PubMed] [Google Scholar]
- Wei D, Yang J, Li W, Wang K, Zhang Q, Qiu J (2014): Increased resting functional connectivity of the medial prefrontal cortex in creativity by means of cognitive stimulation. Cortex 51:92–102. [DOI] [PubMed] [Google Scholar]
- Zhang L, Gan JQ, Wang H (2014): Optimized gamma synchronization enhances functional binding of fronto‐parietal cortices in mathematically gifted adolescents during deductive reasoning. Front Hum Neurosci 8:430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L, Gan JQ, Wang H (2015): Mathematically gifted adolescents mobilize enhanced workspace configuration of theta cortical network during deductive reasoning. Neuroscience 289:334–348. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


