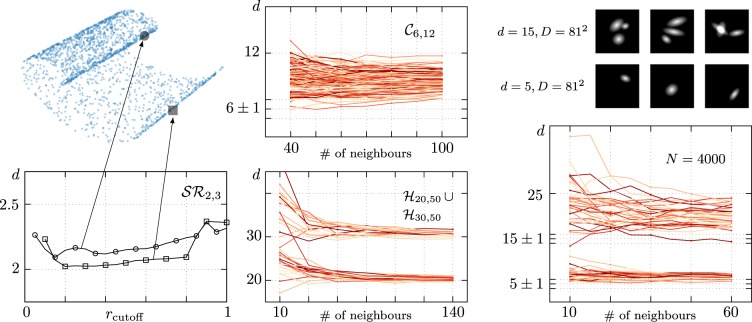
Figure 3.

The multiscale generalization of the FCI estimator provides a state-of-the-art tool to tackle the ID estimation for complex datasets with multidimensional features and high intrinsic curvature. The multiscale FCI method selects single points in the dataset and their neighbours at a fixed maximum distance r_cutoff, which is then varied. The FCI estimator is then used on each neighbourhood, giving an estimation for a local ID d_est(r_cutoff). Crucially, the robustness to extreme local undersampling of the FCI estimator allows to shrink the radius of the neighbourhoods r_cutoff, giving a reliable estimate of local IDs, that appear as pronounced plateaux in the d_est vs r_cutoff plot. Alternatively, one can look at d_est(n), where n is the number of nearest neighbours used in the estimation, keeping more control on the number of points used in the local estimation. (Left) We present an illustrative application of the multiscale FCI method in the case of the Swiss Roll dataset (N = 2000) for two particular samples. Both samples hint to the correct ID estimation d_est = 2. We observe that the sample extracted from the highly curved inner region of the Swiss Roll provides an overestimated ID whereas the sample from the outer and flatter region exhibits a plateau at the correct ID. This suggests to use the minimum d_est reached as an estimator for the true ID, but a more careful analysis is needed. (Top center) We apply the multiscale FCI method to a highly curved manifold ${\mathcal{C}}_{6,12}$ (N = 10000) introduced in¹³, challenging to all ID estimators (see also Materials and methods for its parametric defintion). The local d_est spans the range between the true ID $d_{\mathrm{est}}~6$ to the embedding dimension $D~12$. (Bottom center) We show the multiscale FCI analysis on a multidimensional manifold which is built as the union of two intersecting hypercubes datasets ${\mathscr{H}}_{\mathrm{20,50}}$ and ${\mathscr{H}}_{\mathrm{30,50}}$, each one consisting of N = 1000 samples. At small number of neighbours, we observe spurious effects due to vary sparse sampling of the neighbourhoods; quick convergence to the true IDs is then observed. (Right) As a last validation test, we generate an artifical dataset of bitmap images with multiple “blobs” with five degrees of freedom each (see Materials and methods), that we use as a proxy for curved manifolds of transformations of high contrast images. The multiscale analysis works nicely in either the one (d = 5) and three (d = 15) blob cases, although for multiple blobs we observe that the high curvature reflects in band that spans more than ten dimensions.