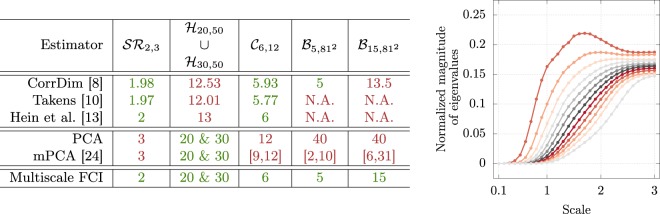
Figure 4.

Comparison between ID estimators on curved and multidimensional datasets. Geometrical methods fail on high-ID datasets, even if the embedding is linear. Global PCA behaves complementarily, retrieving correctly the ID in this case, but losing predictivity on curved datasets. This issue is not fixed by perfoming multiscale PCA, since we often lack a clear signature for estimating the ID, e.g. a gap in the magnitude of the sorted eigenvalues. Even if we use the less stringent criterion (often used in the literature, see for instance²⁴) of identifying the ID as the minimum number of eigenvalues such that their mass ${\sum }_{i\mathrm{=1}}^{\mathrm{ID}}{\lambda }_i/{\sum }_{i\mathrm{=1}}^{\mathrm{D}}{\lambda }_i$ is larger than 0.95, we lack a signature of persistence as in the case of our estimator (the plateau as a function of the cutoff radius). In the right panel we plot the twelve averaged eigenvalues of the correlation matrix of the ${\mathcal{C}}_{6,12}$ manifold as a function of the cutoff scale (the average is performed over all the different balls of the same radius centered around each point) to highlight this issue. No evidence of the correct ID can be found using the common criteria reported above. Where not available (N.A.) is reported, the code of¹³ returned either 0 or infinity. We expect however that the results would be very similar to those obtained with CorrDim.